Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. т а ін. Вища математика у прикладах та задачах. Ч 3

Подождите немного. Документ загружается.

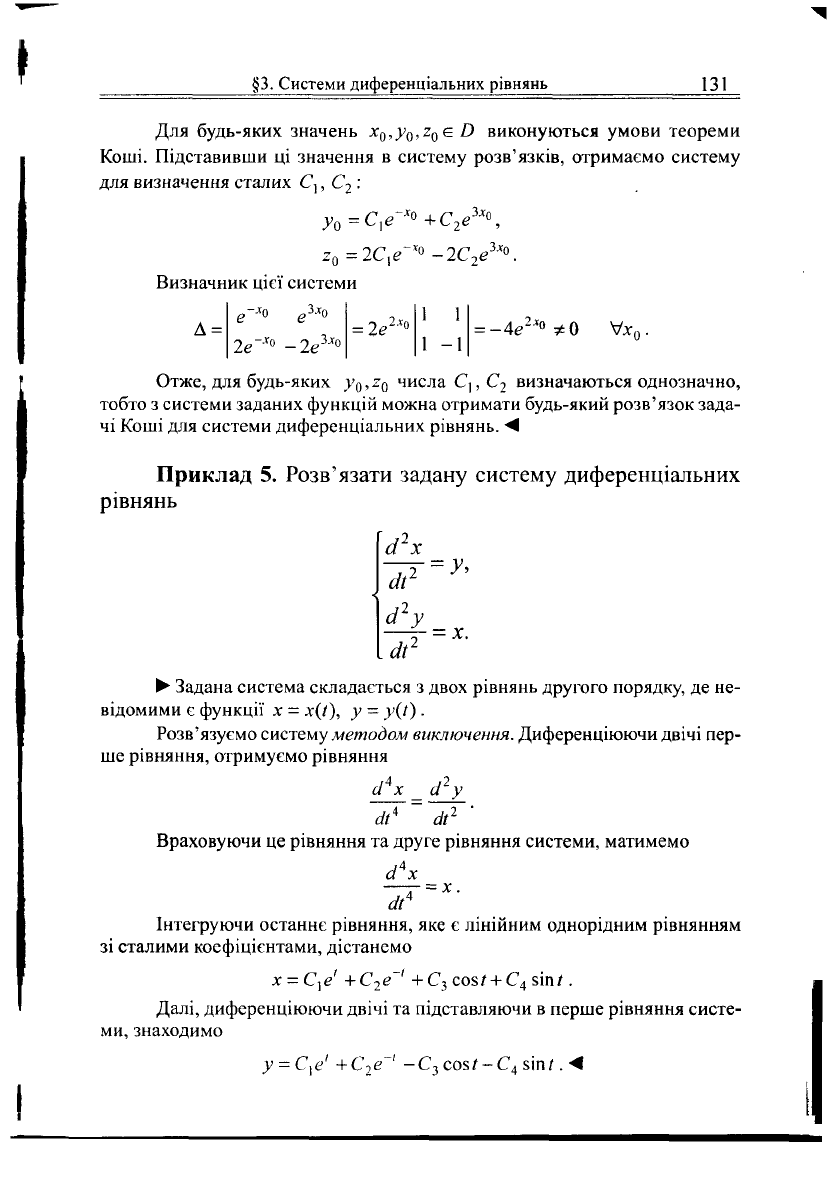
§3.

Системи диференціальних рівнянь

131

Для будь-яких значень х

,у

,г

£>

виконуються умови теореми

Коші. Підставивши

ці

значення

систему розв'язків, отримаємо систему

для визначення сталих

С,, С

'•

Уо

:С,<Г

° +С

ЗЛП

2С,е~

-2С,е

Визначник цієї системи

2е •2е>

= 2е

2х

-1

-4е

2х

Ух,

•

Отже,

для

будь-яких

, і

числа

С,, С

визначаються однозначно,

тобто

системи заданих функцій можна отримати будь-який розв'язок зада-

чі Коші

для

системи диференціальних рівнянь.

Приклад

Розв'язати задану систему диференціальних

рівнянь

сі

•

= у>

сіҐ

• Задана система складається

двох рівнянь другого порядку,

де не-

відомими

функції

х = х(І), у = у{і).

Розв'язуємо систему методом виключення. Диференціюючи двічі пер-

ше рівняння, отримуємо рівняння

сі

сії

Враховуючи

це

рівняння

та

друге рівняння системи, матимемо

сі

сії

•

= х.

Інтегруючи останнє рівняння,

яке є

лінійним однорідним рівнянням

зі сталими коефіцієнтами, дістанемо

= С,е'

+С

е~'

+ С

соз/ + С

зіп/.

Далі, диференціюючи двічі

та

підставляючи

перше рівняння систе-

ми,

знаходимо

= С|<?' + С

е ' -С

соз/-С

зіп /.

132

Глава 1. Диференціальні рівняння

Приклад

Знайти загальний розв'язок системи

диферен-

ціальних рівнянь

-2,

сіх

СІ2 _ 2'

сіх у

частинний

розв'язок,

який задовольняє початкові умови

{\) = \, 2(1) = -і.

• Задана система є нормальною системою диференціальних рівнянь,

що складається з диференціальних рівнянь першого порядку, які не є ліній-

ними. Розв'язуємо \і методом виключення.

Перше рівняння системи продиференціюсмо по х:

Оскільки з другого рівняння системи 2 = —, то у — , але з пер-

У У

шого рівняння 2

(у')

тому система двох рівнянь першого порядку зве-

лась до одного рівняння другого порядку

у =•

(у'У

або

У'У

НУ')

= О.

Ліва частина цього рівняння є

(уу')',

тому

УУ

звідки

уау = —С

]

сіх,

—

=— С,х

+—С-,,

2 ' 2 2 2 -

тобто

у = ±^С

х + С

З першого рівняння системи 2 = -у , тобто

с,

§3.

Системи диференціальних рівнянь

133

Система функцій

±т]С>х

+ С

2уІС

]Х

+ С

утворює загальний розв'язок заданої системи.

Знайдемо частинний розв'язок, використовуючи початкові умови

у(1)

= 1, 2(1) = —-1 та

записавши загальний розв'язок

вигляді:

УІС

]

+ С

,2 = --

]С

]

+ С

(тут взято знак "плюс" перед коренем

виразі

для у, бо

саме

так

можна

задовольнити умову

у(\) = 1, у

виразі

для 2

взято відповідно перший знак

"мінус").

Тоді

1=л/С,+С

, -1 =

С|

Звідси

С, = 1, С

= 0 .

Отже, пара функцій

у = —=

-частинний розв'язок зада-

2<х

ної системи.

Приклад

Показати,

що

систему рівнянь

ІУ

= ху,

[г'

у'

ху

не можна звести

до

одного рівняння.

• Підставивши

у' = ху у

друге рівняння системи, отримуємо систе-

му двох рівнянь,

не

зв'язаних

між

собою

= ху,

2=2.

Розв'язуючи кожне рівняння окремо, знаходимо

= С

х2

/\ г = С

Приклад

Знайти фазову траєкторію автономної дина-

мічної системи

134

Глава

І.

Диференціальні рівняння

СІХ

сії

яка проходить

через

точку

(2,3).

• Розв'язання задачі зводиться

до

знаходження загального розв'язку

заданої системи диференціальних рівнянь. Виключаючи

цього розв'язку

час

І,

отримуємо рівняння фазових траєкторій,

сукупності яких виділимо

ту,

що

проходить через точку Л/

(2,3).

Загальний розв'язок знайдемо методом виключення. Запишемо дру-

ге рівняння системи

вигляді

= у.

Продиференціюємо

це

рівняння

по і

=у

та підставимо

х і х' у

перше рівняння системи. Отримаємо

,,'_(/)

або

уу-(у)

о,

тобто маємо одне рівняння другого порядку

однією невідомою функцією

у .

Поділимо ліву

та

праву частини останнього рівняння

на у

уу-(у)

Тоді

це

рівняння запишеться

так:

сі(у'^

сії

Звідси

або

Звідки, інтегруючи, отримуємо

1пИ =

С,Г

+ 1п|С

§3.

Системи диференціальних рівнянь

135

або

У =

Тоді

= С,С

/''.

Підставивши цей вираз у друге рівняння системи, отримуємо

х =

]

С]І

Отже,

загальний розв'язок системи:

х = С,С

Гі

', у =

С]І

Виключимо з загального розв'язку час І. Отримуємо

х = С

у,

тобто фазовими траєкторіями системи є прямі.

Виділимо пряму, яка проходить через точку М

(2,3):

2 = С,

•

З, С, = -.

Отже,

фазова траєкторія, що проходить через точку М

(2,3), має рів-

няння

= —X.Л

Лінійні

системи диференціальних рівнянь

із

змінними коефіцієнтами

Приклад

9. Розв'язати задану систему диференціальних

рівнянь

сіх

—

= —

У,

сії

сіу_

_2х_ у_

сії

і'

•

Маємо лінійну однорідну систему диференціальних рівнянь із змін-

ними коефіцієнтами. Розв'язуємо її методом виключення.

З першого рівняння системи знаходимо

у = X ч .

Звідки

ІГ 1 / X

136

Глава 1. Диференціальні рівняння

Підставляємо у та у у друге рівняння системи

, 1 , х 2х 1( , х

х +- х —- = —г

+ -

х + —

І І

і 1\ І

Звідки

** = 0.

Інтегруючи це рівняння, отримуємо

дг'

= С,,

х = С,/ + С

тт • ' X

Далі, враховуючи, що у = х + —, отримуємо

У = С\ +•

І + С

= 2С, +

С,

Загальний розв'язок системи

х = С

І + С

у = С

] +

Сі

+ С2

= 2С,+^, /*<>.««.

Приклад 10. Знайти розв'язок системи диференціальних

рівнянь

сіу _ 2х

сії і

який задовольняє початкові умови

х(-1) = 1, у(-\) = -2.

• Маємо лінійну однорідну систему диференціальних рівнянь із змін-

ними коефіцієнтами. Розв'язуємо її методом виключення.

сі

х _ ау _ 2

а-Ґ

Ж і

або

<І

•2х = 0.

Отримали однорідне рівняння Ейлера, розв'язок якого шукаємо у виг-

ляді х = І

§3.

Системи диференціальних рівнянь

137

Підставляючи

та

х"-к(к-\)і

на

/*,

отримуємо характеристичне рівняння

А(А

-1)-2 = 0

або

-к-2

корені якого

А, = 2, к

-1.

Загальний розв'язок рівняння Ейлера

в рівняння

та

скорочуючи

Ґ +-

С,

Звідси

2С,/

—

Підставляючи

цс в

перше рівняння, маємо

Отже, загальний розв'язок заданої системи

х =

+^-,

2Са-Щ-.

Враховуючи початкові умови, знаходимо сталі

, С

Гдг(-І)

= С,-С

=1,

Ь(-1)

-2С,-С

=-2.

Звідси

С, = 1, С

= 0.

Отже, шуканий розв'язок гакий:

х = і

, у = 2і. М

Приклад 11. Розв'язати систему диференціальних рівнянь

СІХ

2х

+1,

•

Маємо

лінійну неоднорідну систему диференціальних рівнянь

із

змін-

ними коефіцієнтами.

138

Глава 1. Диференціальні рівняння

Перше рівняння системи розв'язуємо незалежно від другого. Запи-

шемо його у вигляді

х'

+ -х-\ = 0.

Це лінійне диференціальне рівняння першого порядку відносно х та

х',

розв'язання якого можна виконати методом Бернуллі, використовуючи

підстановку

х = и{і)

•

У(І) .

Після розв'язання отримаємо

(перевірте!)

Підставляючи х(1) у друге рівняння системи, отримуємо

'_ -І £і

2С

~з

Р з'

Це теж лінійне диференціальне рівняння першого порядку відносно

у та у'. Розв'язавши це рівняння, отримуємо

У = С

е ----

(перевірте!)

Отже, загальний розв'язок системи

, ч

І '

і З

с,

+ С

е' --, /^0.

Лінійні однорідні системи диференціальних

рівнянь зі сталими коефіцієнтами

Приклад 12. Розв'язати задану систему диференціальних

рівнянь

СІХ

СІЇ

ДУ_

СІЇ

= х + 2у,

= 4х + 3у

двома способами: 1) методом виключення; 2) методом Ейлера.

§3.

Системи диференціальних рівнянь

139

• Задана система є лінійною однорідною системою зі сталими кое-

фіцієнтами, де невідомими є функції х = х((), у = у((). Система відпові-

дає випадку, коли корені характеристичного рівняння дійсні та різні (див.

розв'язання). Розв'язання системи виконаємо двома способами.

Спосіб 1. Метод виключення (зведення до однорідного диференціаль-

ного рівняння другого порядку).

Запишемо задану систему у вигляді

їх'

—

х + 2у,

}у' = 4х + 3у.

З першого рівняння системи знаходимо у :

1 , 1

Звідси

у = —х —X .

2 2

,1,1,

у = —х X .

2 2

Підставимо у та у' у друге рівняння системи:

—х х = 4х + 3

2 2

-х х

^ 2 2

Після перетворень отримуємо

х*-4х'-5х = 0.

Нелінійне однорідне диференціальне рівняння другого порядку зі ста-

лими коефіцієнтами, розв'язання якого виконується відомим методом.

Записуємо характеристичне рівняння

-4*-5 = 0 .

Корені його А] = 5, к

=-\ - дійсні та різні.

Отже, загальний розв'язок отриманого рівняння є

х(і) = С

]

' +

Далі знаходимо х':

х' = 5С,е

' -С

Підставимо х га х' у вираз для визначення функції у :

у = ±{5С

]

ІІ

-С

е->)-±{

Сі

е-')=2С^' -С

е" .

Отже, загальний розв'язок заданої системи такий:

х(/) = С,е

' +С

е~',

у{1) = 2С

' -С

е~'.

140

Глава 1. Диференціальні рівняння

Спосіб 2. Метод Ейлера (за допомогою характеристичного рівняння).

Для заданої системи

сіх „

—- = х + 2у,

СІЇ

± = 4х

3у,

сії

• А І

матриця якої А = | ^ І, складаємо характеристичне рівняння:

с!еІ(А-ХЕ) =

1-Х 2

4 3-Я,

= 0

або,

після перетворень

А? -

4А,

- 5 = 0,

яке має корені А,, = 5, Х

=-1 - дійсні та різні.

Частинні лінійно незалежні розв'язки системи Х

(

^''(/) і Х

'(?) за-

пишемо у вигляді:

Х^\і)

У^е

ІІ

а2)

(/)-У

(

"',

де у'^^у^г) - власні веісгори, які відповідають власним значенням А, та Х

Знаходимо ці власні вектори з системи рівнянь

Г(ї-А)х + 2у = 0,

[ 4х + (3-А)>> = 0.

Підставимо послідовно А,, та Х

в записану систему:

а) Л., = 5.

Отримуємо однорідну систему, у якій два рівняння еквівалентні, і тому

розв'язання її виконується гак:

-4х+2>; = 0, \х = С,

==> у = 2х => <

4х-2у = 0 Ь = 2С

Нехай, наприклад, С = 1, тоді власний вектор V =

б)

=-1.

Маємо систему рівнянь:

Г2х+2у = 0,

=> х

—

-у

\х = С,

[4х-4у=0 " \у = -С.

Нехай, наприклад, С = 1, тоді власний вектор