Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. т а ін. Вища математика у прикладах та задачах. Ч 3
Подождите немного. Документ загружается.


§2.
Функціональні ряди. Степеневі ряди
201
тобто хе — + кк, — + кп [ кєХ.
ІЗ 3 )
При х = + — + кл не виконується необхідна умова збіжності.
Отже, область збіжності заданого ряду: х є | у + кк, ^~ + кп \ к є 2 .
С05ИХ
и=0 Є
Необхідна умова збіжності виконується тільки при х > 0 .
Оскільки
»Л
Х
)\
=
со&пх
1
а при х>0 ряд
1
X—
пх
збігається за радикальною ознакою Коші:
1 1
і
= — <1,
пх „X
Є Є
то заданий ряд
созга:
я=0 Є
збігається за ознакою порівняння при х > 0 .
Отже, область збіжності заданого ряду: 0< х <+°° .А
Приклад 2. Дослідити на рівномірну збіжність на зазна-
чених проміжках задані функціональні ряди.
(-1)
/7-1
,(-оо,+оо); б)
Х>",
(-1Л);
и = 1
*)Х
8Іп"
ПХ
п=1 П
. ~ СОЗПХ . .
(-оо, + оо) ; г) X Г"
»
(-°°, + °°)
•

202
Глава
2.
Ряди
~ /
,
_П""
1
•
а
)
IV—'
(-~'
+
°°)-
Скористаємось означенням рівномірно збіжного ряду, згідно
з
яким
ряд
є
рівномірно збіжним, якщо
\/є>0 З/У є N , що для
всіх
п> N і
Ухє[а,Ь] виконується нерівність |/•„
(х) | < є.
При будь-якому
х
заданий
ряд
збіжний
за
ознакою Лейбніца, тому
його
п -й
залишок оцінюється
за
допомогою нерівності
К(*)|<К
+
|(*)|=
2(п+]
!
-<—
1
—
ДЛЯ Ухє(-оо, +
оо).
х
к
>+п+\
п+1
Оскільки
—ї— < е , як
тільки
п >
—
-1,
візьмемо
/У(є) =
—
-
1
.
Отже,
/7+1
є Є
для всіх
/7
>
/У(Е)
= —
1
матимемо,
що
І
г„
(х)
І
< є. Це
означає,
що ряд
збіж-
є
ний
на
проміжку
(-», + °°).
б)
|>" ,
(-1,1).
л = і
В інтервалі
(-1, 1) ряд
збігається,
бо є
геометричним рядом,
для
яко-
го
| ц
І
=
І
х
І
< 1.
Залишок ряду
/-„(х)
=
х"
+,
+х
я+2
+...=
ІУ •
к=п+1 '
Х
Для залишку
г
п
(х)
маємо:
Ііт
,,
К(*)| = 7> і™
\г„(х)\
= оо,
д—>-1+0
2
*->1-0
Отже, прийнявши Є
> ^, не
можна досягти виконання нерівності
|
і",,(х)
| < є для Ух є
(-1,1). Згідно
з
означенням рівномірно збіжного ряду,
ряд
не є
рівномірно збіжним
на
проміжку
(-1, 1).
.
^
зіп"
пх
В)
2, 2 '
(-°°'
+00
)-
/1
= 1
п
Скористаємось ознакою Вейєрштрасса, згідно
з
якою, якщо даний
ряд
^и
п
(х)
на
проміжку
має
мажорантний, тобто збіжний числовий
ряд
/і =
1
и=1
з додатними членами, такий,
що | и
п
(х)
\
< а
п
, то
даний ряд рівномірно збіж-
ний
на
цьому проміжку.

§2.
Функціональні ряди. Степеневі ряди
203
Врахуємо, що | и„ (х) |
=
51П
пх
У хе
(—оо, +°°).
Ряд
_
збіжний» отже, він є мажорантним для заданого ряду.
Звідси заданий ряд є рівномірно збіжним на проміжку (-оо, + оо).
~
С08ИХ
г) X"
7І
•,
(-°°, + °°) •
я=1
п
-
Скористаємось ознакою Вейєрштрасса
1
Врахуємо, що | и„ (х) | =
С05ЯХ
?!
<— УХЄ (-оо, +оо) .
и!
Ряд X збіжний (за ознакою Даламбера), отже, він є мажорант-
я=1'
ним для заданого ряду. Звідси заданий ряд є рівномірно збіжним на проміж-
ку (-оо, +
оо)
Степеневі ряди
Приклад
3.
Визначити область збіжності степеневого ряду.
а)
Х^г;
„=\П
б)
Хс-іГ
1
»";
я=1
/7
=
1
д) X
/7
= 1 П
х"
оо П
/7
= 1
е)
ХЧ^г(*
+
2)"
/7
= 1 П-1
•а) X
Знайдемо радіус збіжності К за формулою К= Ііт
1
-"л+1
.
Оскільки
И
(и + 1)
,
маємо
/? = Ііт
"<я+1
= Ііт — = Ііт
-—-Т
1
-
п
+ \~п
П—>оо
= Ііт — = 1.
(л + 1)
2

204
Глава 2. Ряди
Отже, ряд збігається абсолютно для всіх х, таких, що | х | < 1, тобто
інтервал збіжності ряду (-1, 1).
Дослідимо на збіжність даний ряд на кінцях інтервалу збіжності, тоб-
то при х =
—1,
х -
1
.
°° 1
При х =
1
отримуємо числовий ряд Х~Т • Ц
еи
Р
яд
збіжний, бо є
п = \П
узагальненим гармонічним при р = 2 > 1.
При х = -1 отримуємо числовий ряд X
(-1)"
Цей ряд абсолютно
п = 1 "
збіжний, бо ряд, складений з абсолютних величин його членів , збіжний.
п = \П
Отже, область збіжності даного ряду така: [-1, 1].
Зауважимо, що для знаходження радіуса та інтервалу збіжності мож-
на використати безпосередньо ознаку Даламбера, тобто виходити з умови,
и
п
+і О)
що,
коли Ііт
и„(х)
У даному випадку
< 1, то ряд збіжний.
іл+1
К(*)|
= М-
п
I (*)
І
= '
Ііт
«»+](*)
"„(*)
Ііт
І |Л
+1
2
X П
(и + 1)
2
2 '
•= Ііт X = X .
І)
2
|х|" "'^-(и-г-1)
2
За ознакою Даламбера ряд буде збіжний, якщо |х|<1 . Звідси
-1 < х < 1.
Отже, радіус збіжності К = 1, інтервал збіжності (-1,1).
Як показано вище, областю збіжності розглядуваного ряду є відрізок
[-1,1]
•
б) ХС-ІГ'пх".
л = 1
Для знаходження радіуса збіжності Я скористаємось формулою
К= ІІТ
*и+1
Оскільки а
п
=(-1)" п,
а
п+х
=(-!)"(« +1), маємо
К = Ііт
^л+1
- Ііт
[(-І)""'
/7
I
І
(-!)"(«+
1)1
•= Ііт
п +
1
І.

§2.
Функціональні ряди. Степеневі ряди
205
Отже, ряд збігається абсолютно для всіх х, таких, що | х | < 1, тобто
інтервал збіжності ряду (-1, 1).
Дослідимо збіжність на кінцях інтервалу збіжності.
При х = -1 отримуємо числовий ряд
/7=1 /7 = 1 /7 = !
Цей ряд розбіжний, бо Ііт и
п
= Ііт (-п) * 0 .
При х =
1
маємо числовий ряд
п
>
для якого
1і
т и
„ =
/7 = 1
= Ііт (-І)""
1
п не існує, отже, цей ряд розбіжний.
Отже, областю збіжності даного ряду є інтервал: (-1,1). '
в) |>!х" •
/7 = 1
Для знаходження радіуса збіжності Я скористаємось формулою
Я= Ііт
Оскільки а
п
=«!, а
и+1
= (п + І)!, маємо
/?= Ііт Ііт
п\
пт
=
0.
Рівність /? = 0 означає, що ряд збігається тільки в точці х = 0 .
Отже, область збіжності даного ряду складається з однієї точки х = 0 .
г) У—-
У
^ Т/7
/7 =
1^
Знайдемо радіус збіжності Я за формулою Я = Ііт . Оскільки
а„ = —, маємо
„ ,• 1 1
Я = пт .—- = Ііт .— = 2 .
»->-7кі
»-*-„/_]_
Отже, інтервал збіжності (-2, 2).
Дослідимо на збіжність даний ряд на кінцях інтервалу збіжності, тоб-
то при х = -2, х = 2 .

206
Глава 2. Ряди
При х - 2 маємо числовий ряд X—
=
X' • Ч
еи
Р
ад
розбіжний, бо
и =
і2
я =
1
Ііт и =
1
*0.
При * = -2 маємо числовий ряд X
(-1)"2"
л = 1
^
Х(-0"
-
Цей рядроз-
біжний, бо Ііт и
п
- Ііт (-1)" не існує.
Отже,
область збіжності даного ряду співпадає з інтервалом збіжнос-
ті,
тобто областю збіжності є інтервал: (-2, 2).
л = 1
П
Знайдемо радіус збіжності К за формулою К= Ііт ._!— . Оскільки
(-1)"
а
п
- , маємо
К=
Ііт
Ііт
(-1)"
= Ііт — = Ііт п = °° ,
Отже,
інтервал збіжності (-°°, + °°) . Область збіжності даного ряду
співпадає з інтервалом збіжності, тобто область збіжності така: (-°°, +°°).
Радіус збіжності К знаходимо за формулою К = Ііт
/1->ос
(-І)""' (-1)"
ки а„ = '—, а„
+]
.Л
и+1
^аємо
•
і
л+1
.
Оскіль-
и-2"
(и + 1)2
Л= Ііт
(_!)-!
Ял
= Ііт -
а
л+1
= Ііт -
(л + 1)2
я+|
..
+ -2
Ііт
л+1
«•2
й
Ііт 2| 1+- 1=2.
Отже,
ряд збігається абсолютно для всіх я:, що задовольняють нерів-
ність | х +
21
< 2, тобто -2 < х + 2 < 2.

§2.
Функціональні ряди. Степеневі ряди
207
Звідки -4 < х < 0 - інтервал збіжності, Я = 2 - радіус збіжності.
Дослідимо збіжність на кінцях інтервалу збіжності.
При х = —4 отримуємо числовий ряд
>я-1
„=і п-2"
я=1
и
який розбігається (гармонічний ряд).
При х = 0 маємо числовий ряд
и = 1 «-2 п = \
п
який збігається умовно (ряд збігається за ознакою Лейбніца, а ряд, складе-
ний з абсолютних величин його членів, розбіжний, бо є гармонічним).
Отже, область збіжності даного ряду : (-4, 0].
Зауважимо, що для знаходження радіуса та інтервалу збіжності мож-
на використати безпосередньо ознаку Даламбера, тобто виходити з умови
и«+і(*)
того,
що, якщо Ііт
У даному випадку
|х + 2
< 1 , то ряд збіжний.
Ііт
и„(х)
Ііт
п-2"
\х + 2
іи+І
\х + 2\"
+і
-п-2"
(« + 1)2
х + 2
Л + І
"^~(и + 1)-2
п+|
-|х + 2|"
Ііт
х + 2
>
п+
1
За ознакою Даламбера ряд абсолютно збіжний, якщо
х + 2
< 1. Звід-
си | х +
21
< 2 , або -2 < х + 2 < 2, або -4 < х < 0 .
Отже, радіус збіжності Я = 2, інтервал збіжності (-4, 0). ^
Приклад 4. Знайти суми заданих степеневих рядів, вико-
ристовуючи почленне диференціювання та інтегрування.
.2л+1
л=0
2п
+ 1
і»=1 л
х
І
< 1;
в) £их
и =
1
л-1
X <1.
2п -1
г) І"
и=1 2.

208
Глава 2. Ряди
оо і .\Л 2я+1
и = 0
2п + 1
Позначимо суму заданого ряду через 8{х), тобто
~ ( \\
П
г
2п+1
£(*)=2
(
І , ,
М<і.
„=о 2«+1
Тоді
п=0
Цю суму можна розглядати як геометричну прогресію з першим чле-
ном а - 1 і знаменником д = -х
2
. Оскільки | х
\
< 1, то | д\ <
1
. Знайшовши
суму спадної геометричної прогресії за формулою •У =
а
, дістанемо
1-д
1
-ХНУ*
2
".
1
+ х
л=0
Інтегруючи цю рівність на відрізку [0, х] с (-1,1), маємо
|5'(х)с& = /
( оо Л
Х(-1)"х
2
"
я=0
сіх
= ]
1
1+х^
сіх.
Звідки
оо
С_і\Л
г
2л+1
3(х) = X !; , =агс1§х,
|х|<1.
л = 0
2п + \
б)
|х|<1.
л=1
л
Позначимо суму заданого ряду через 5(х), тобто
5(х)=2— • Ме-
тоді
н=1
5'(х)=
2
х
""
1
=!
+
*
+
*
+•••,
М<1-
Цю суму можна розглядати як геометричну прогресію, де а =
1
і ц - х,
|?|
= |х|<1.Тоді
5'(х) =
т
1-=£х
и
-
1
.
1-х
л=1
Інтегруючи цю рівність на відрізку [0, х] с (-1,1), маємо
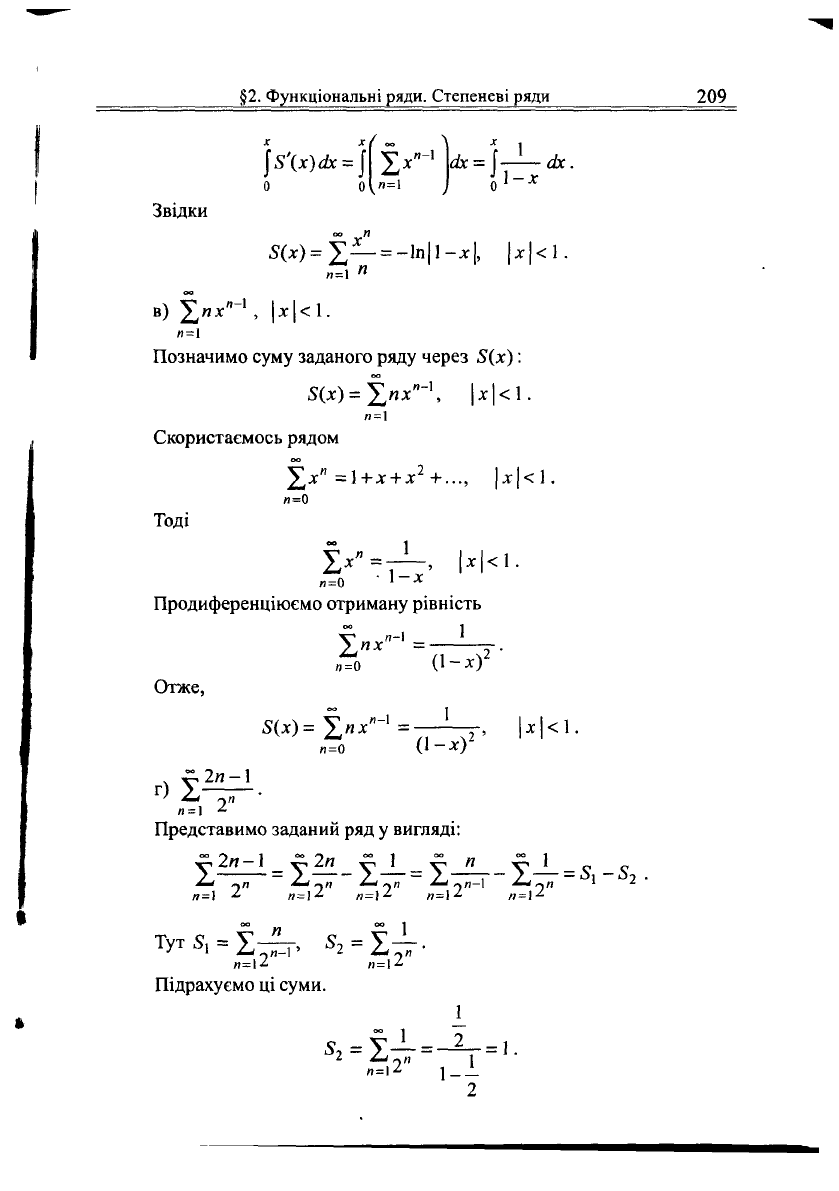
§2.
Функціональні ряди. Степеневі ряди
209
\Б\х)ах = \ |>
и
-' ]& =
}_!_<&.
Звідки
5(х)=£—
= -1п|і-х|,
|х|<1.
л=1
в) ,
|х|<1.
я = 1
Позначимо суму заданого ряду через 5(х):
8(х)=^пх"-\
\х\<\.
л = 1
Скористаємось рядом
£*" = 1+х + х
2
+ ...,
|х|<1.
и=0
Тоді
|х|<1.
л=0
Продиференціюємо отриману рівність
п=0
(1-х)
2
'
Отже,
.«-1
І
5(д
С
)=Іих-
1
=-
,
л=0
О"*)
|х|<1.
л = 1
Представимо заданий ряд у вигляді:
у2«-1
=
у2я у 1
=
у п у_}_
= 5
_
5
я = 1
/ »=)/ »=1^
л =
1^
л
= !^
ТУТ
5, = 2-5- 5
2 =
І^.
л =
1^
Я = І^
Підрахуємо ці суми.
л=і2
^
1--

210
Глава
2.
Ряди
Для знаходження
5, = 2^
п-|
скористаємось допоміжним степеневим
и=і2
рядом
У
ПХ
,
таким,
що при х =
1
приймає вигляд
У " = 5, .
Вказа-
л = 1 я =
1~
ний допоміжний
ряд
збіжний
на
інтервалі
(-2, 2),
позначимо його суму
5(х):
5
«-І-^ГГ'
*є(-2,2).
л = 1
*
Проінтегруємо
цей ряд
почленно
К)А = }І^-Л=І^Г.
«(-2,2).
«=т2"-'
!_£ 2-х
2
Отже,
2х
\8{Х)ІІХ-
о
2
~*
Продиференціюємо ліву
та
праву частини
по х :
2(2-х)-2х(-1)
4
5(х)
=
-
(2-х)
2
(2-х)
2
Тоді
5(1) = 4, але 5(1) =£— = 5,.
л=і2
Отже,
5, = 4 .
Остаточно маємо
Приклад
5.
Розкласти в ряд Маюіорена функцію
/(х) =
зіп
2
х
та знайти область,
в
якій ряд збігається
до
цієї функції.
• Спосіб
1.
/(х) =
5ІП
2
X .
Ряд Маклорена
для
функції
/(х) має
вигляд
к
=
0
*! 1! 2! и!
