Теоретическая механика - теория, задания и примеры решения задач

Подождите немного. Документ загружается.

280

Задача Д.9. Определение устойчивого

положения равновесия механической системы

с одной степенью свободы

Для механической системы (рис. 179 - 181), состоящей из одно-

родных твердых тел и пружин, заданы:

321

m,m,m - массы соответ-

ствующих тел;

12 1 2

,,,,,rr r RR R - радиусы цилиндров и цилиндри-

ческих поверхностей;

,,cc c - коэффициенты жесткости пружин;

123 4

,,,llll- размеры весомых стержней.

В указанном положении механизм находится в равновесии, при

этом примем, что промежуточные стержни и пружины не имеют массы;

проскальзывание цилиндров и сопротивление движению отсутствуют;

пружины в данном положении не деформированы.

Определить условие устойчивости заданного равновесного по-

ложения механизма, если

2cc

Устойчивость положения равновесия

Равновесное положение механической системы может быть ус-

тойчивым и неустойчивым. Если механическую систему вывести из

положения равновесия путем внешних возмущений и предоставить

самой себе, после чего система возвращается в свое первоначаль-

ное состояние равновесия, то такое положение системы называют –

устойчивое положение равновесия. Какие существуют условия тако-

го состояния механической системы?

Для

механической системы с одной степенью свободы в практике

используется теорема Лагранжа-Дирихле

Дирихле Лежен (13.02.1805 – 5.05.1859). Немецкий математик, член Бер-

линской АН. Исследования относятся к теории чисел, математическому анали-

зу, теории уравнений математической физики.

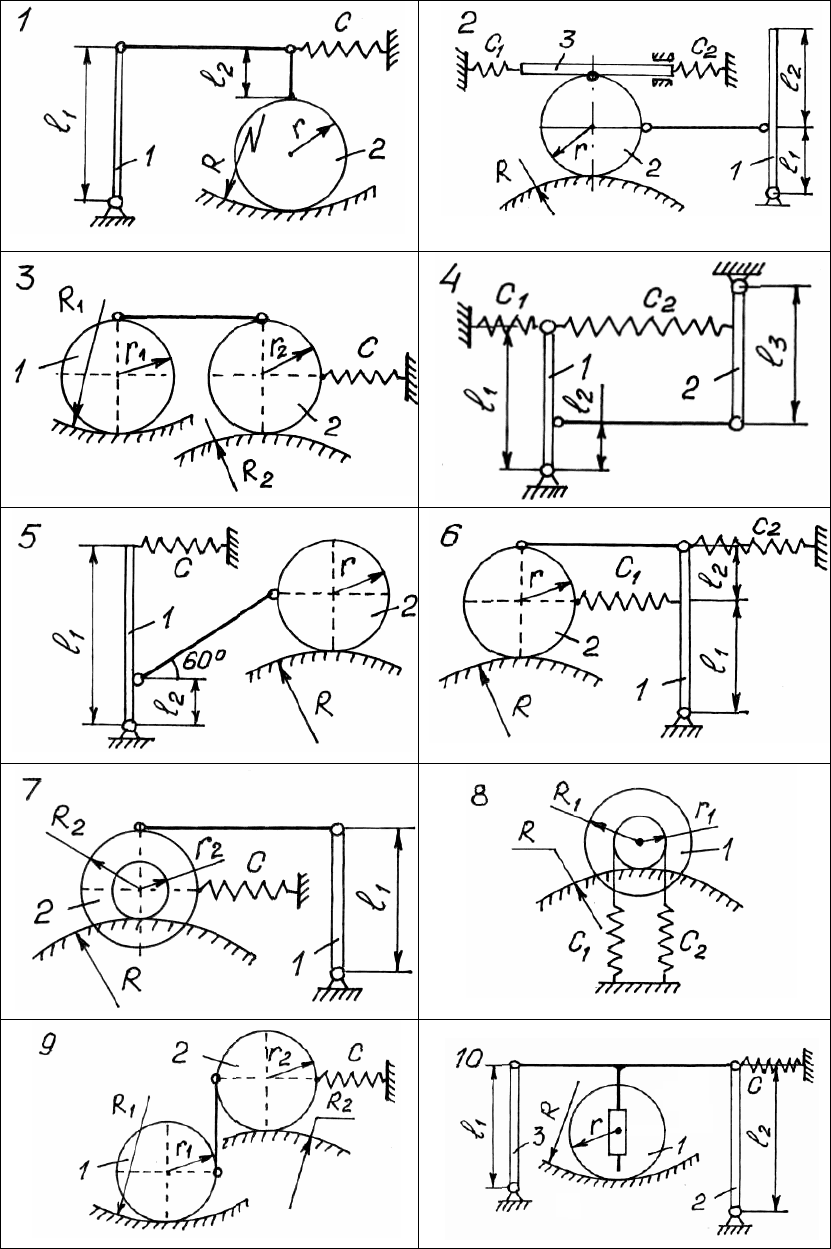
281

Рис. 179

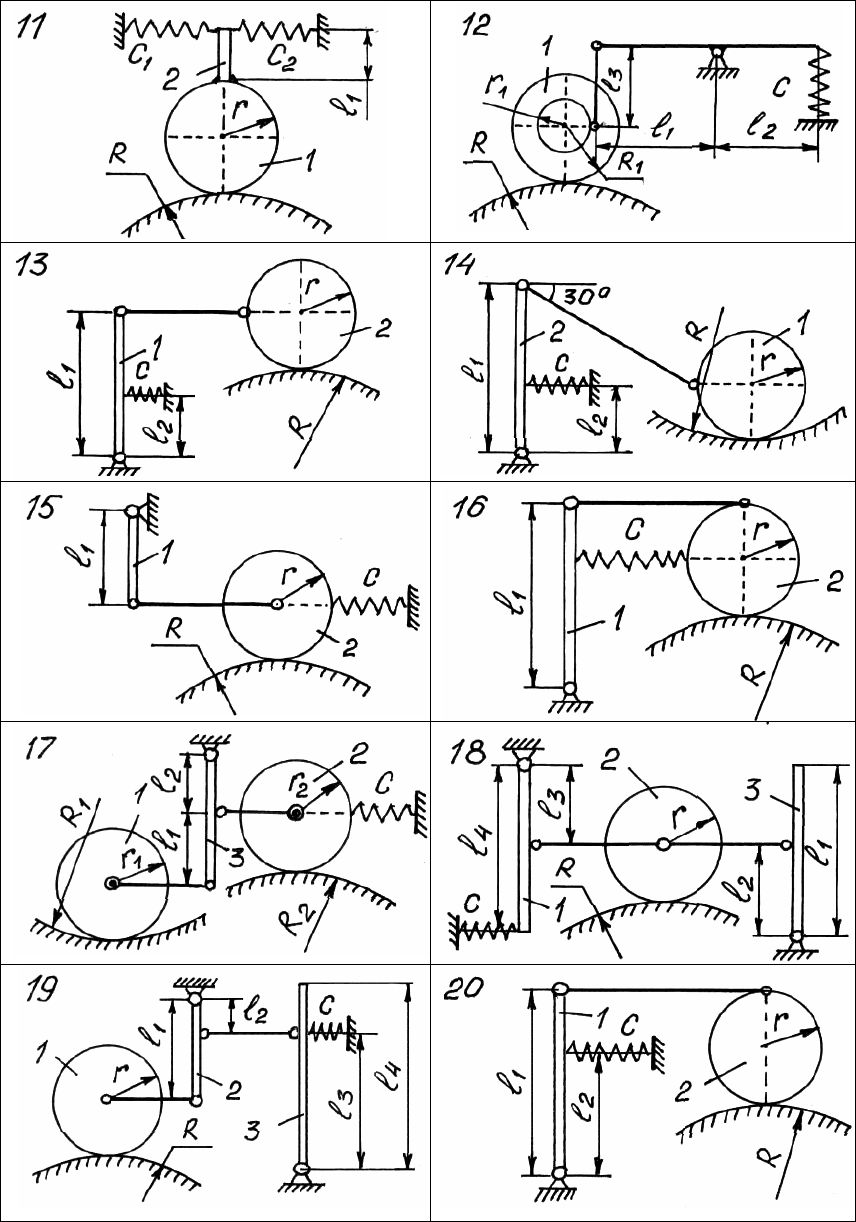
282

Рис. 180

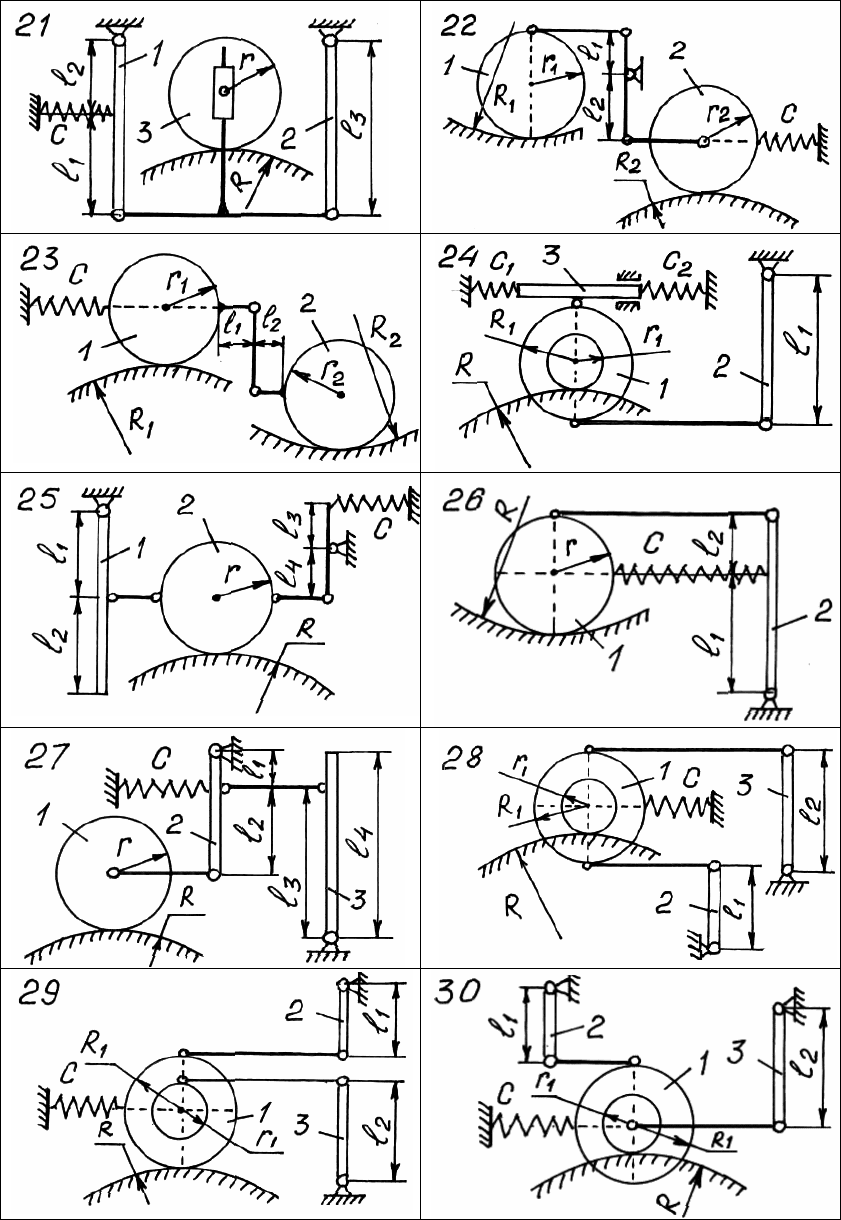
283

Рис. 181

284

Положение равновесия консервативной механической системы с

идеальными, склерономными, голономными связями является ус-

тойчивым, если потенциальная энергия в этом положении имеет

строгий минимум.

Потенциальная энергия есть функция обобщенной

координаты

)

(

ПП =

Необходимое условие равновесия

∂

Решая это уравнение относительно

q , находим то значение

обобщенной координаты, при которой данная система может нахо-

диться в равновесии.

Достаточное условие

∂

Это неравенство налагает условия на коэффициенты жесткости

упругих элементов механической системы для ее устойчивого по-

ложения равновесия.

Но, если потенциальная энергия механической системы с

степенями свободы не имеет минимума, то как исследовать ее не-

устойчивость положения равновесия.

Этот вопрос исследовал А.М. Ляпунов (1857-1918), русский мате-

матик и механик, результаты исследования изложены в докторской

диссертации: “Общая задача об устойчивости движения” (1892г).

Пусть потенциальная энергия есть функция нескольких обоб-

щенных координат

(, , , )

ППqq q= … . В общем виде разложим

потенциальную энергию в ряд Маклорена

до членов второго по-

рядка малости.

i αβ

ПП

ПП qqq

qqq

⎛⎞

∂∂

=+ + +

⎜⎟

∂∂∂

⎝⎠

∑∑

 .

Маклорен Колин (1698 – 14.06.1746). Шотландский математик, основные

исследования посвящены математическому анализу и геометрии.

285

При этом

0П = - принимаем за нулевой уровень,

⎛⎞

∂

−= =

⎜⎟

∂

⎝⎠

- условие равновесия системы.

Остается квадратичная функция потенциальной энергии

П qq

βαβ

αβ

′

∑

αβ βα

αβ

⎛⎞

∂

⎜⎟

∂∂

⎝⎠

- коэффициенты жесткости.

К примеру, если

(, )ППqq= , то квадратичная функция потен-

циальной энергии будет иметь вид

11 1 12 1 2 22 2

(2 )

Псqcqqcq=+ +

Первая теорема Ляпунова

Равновесие консервативной системы неустойчиво, если отсут-

ствие минимума потенциальной энергии можно установить по чле-

нам второго порядка малости в разложении потенциальной энергии

в ряд.

Вторая теорема Ляпунова

Равновесие консервативной системы неустойчиво, если потен-

циальная энергия имеет максимум и наличие можно установить по

членам низшего порядка малости в разложении потенциальной

энергии в ряд в окрестности положения равновесия.

Критерий Сильвестра

Если квадратичная форма

′

определенно положительна, т.е.

вблизи положения равновесия потенциальная энергия будет поло-

жительной, а при

qq q====… , 0

)

(

, то в этом поло-

жении будет строгий минимум, положение равновесия – устойчиво.

Сильвестор Джеймс Джозеф (3.09.1814 – 15.03.1897). Английский мате-

матик. Основные положения относятся к алгебре, теории инвариантов, теории

матриц, теоретической и прикладной кинематике.

286

Критерий устойчивого положения равновесия

Чтобы квадратичная форма

′

была определенно положитель-

на, необходимо и достаточно, чтобы все главные диагональные

миноры матрицы коэффициентов жесткости квадратичной формы

′

были положительны.

11 12 13 1

21 22 23 2

31 32 33 3

123

sss ss

ccc c

cc c c

⎛⎞

⎜⎟

⎝⎠

…

…………………

…

Необходимо и достаточно, чтобы

111

∆

0,c

11 12

21 22

∆

………………………

11 1

∆

sss

……

…………

……

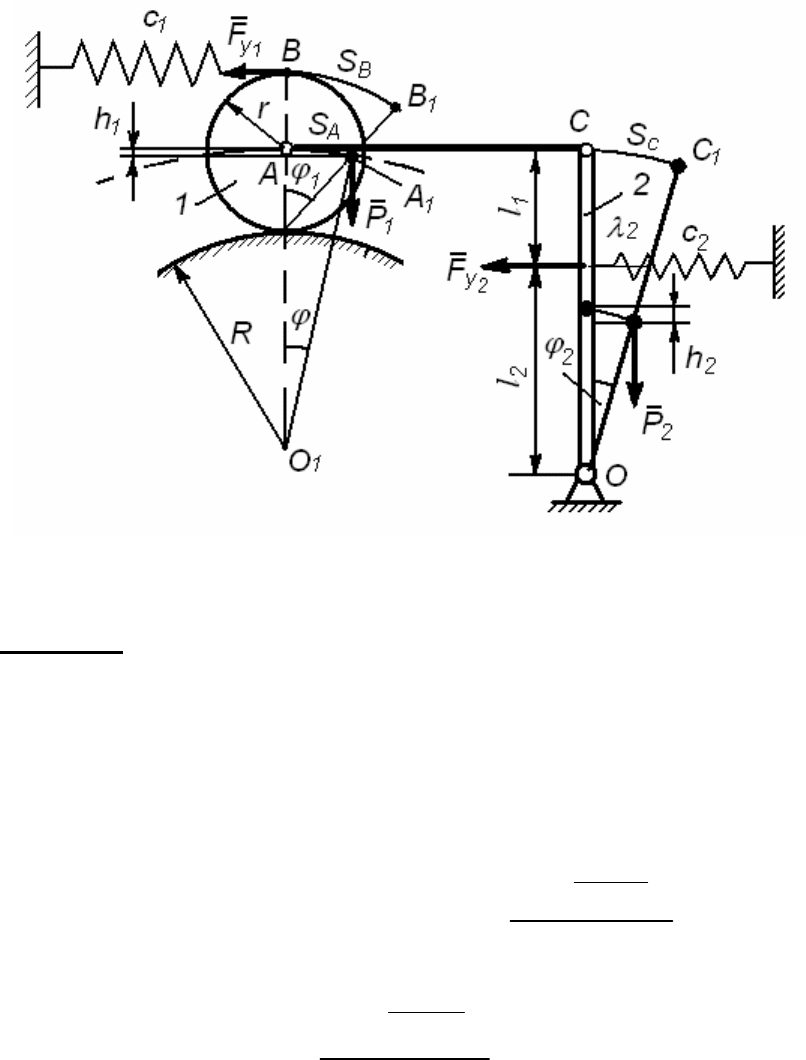
Пример решения задачи

Консервативная механическая система (рис. 182) находится в

равновесии.

Дано:

m - масса цилиндра 1;

m - масса стержня 2,

,cc - ко-

эффициенты жесткости пружин

(

)

2cc

; ,rR - радиусы цилинд-

ра 1 и цилиндрической поверхности;

+lll - длина стержня 2.

Пружины не напряжены и масса стержня

равна нулю.

287

Определить условие устойчивости заданного равновесного по-

ложения механизма.

Рис. 182

Решение

За обобщенную координату принимаем угол

φ между отрезками

AO при качении цилиндра 1 по цилиндрической поверхно-

сти.

При бесконечно малых углах отклонения

φ можно записать сле-

дующие соотношения:

()

SRrφ=+ ;

Srφ

;

φφ

= ;

22()

SS Rrφ==+; ()

SS Rrφ

=+ ;

122

()

S φ=+ll ;

φφ

+ll

В механической системе действуют консервативные силы:

288

Pmg= ;

Pmg= - силы тяжести тел 1, 2;

- силы

упругости пружин.

Вычисляем потенциальную энергию

1212

() ( ) () ( )ППс Пс ПP П P=+++,

1111

() ()

Пс Ac cλ=− =

При

2( )

λ SRrφ== +

() 2( )Пс с Rrφ=+

;

2222

() ()

Пс Ac c λ=− =

Деформации

222

()

λφ φ

Тогда при

c2c =

()

с Rr

Пс φ

1111

() ()П PAPPh=− = ,

()()(1cos)hRrRr φ

+− + − .

Функцию

φco

разлагаем в ряд до членов второго порядка

малости

cos 1

φφ

−+…, откуда

1cos

φφ−≅

Тогда

() ( )

П PmgRrφ=− +

2222

() ()П PAPPh

−=−.

Применяя тот же способ, находим

212

()

h φ=+

ll . Запишем

2212

() ( )

П Pmgφ=− +

ll .

Для всей системы

[]

22 2

11212

() 1

22() ()()

()

Пс Rr φ mR r m gφ

⎡⎤

=++ −+++

⎢⎥

⎣⎦

289

Применяем теорему Лагранжа-Дирихле.

∂

[]

11212

()

22( ) ( ) ( ) 0

()

с Rr φ mR r m gφ

⎡⎤

++ − ++ + =

⎢⎥

⎣⎦

Только при

0=φ

будет положение равновесия механизма.

∂

[]

11212

()

22() ()()0

()

cRr mRrm g

⎡⎤

++ − ++ + >

⎢⎥

⎣⎦

Откуда

[

]

1 212 12

222

12 2

()()()

2( ) 2( )

mR r m g

++ + +

⎡⎤

+++

⎣⎦

ll ll

ll l

При таком достаточном условии механизм будет находиться в

устойчивом положении равновесия.