Теоретическая механика - теория, задания и примеры решения задач
Подождите немного. Документ загружается.

270
где
22
22
12 3
22
22
3
8
r
mm m
RR
ρ
=+ +a - коэффициент инерции (приве-
денная масса).
2
1
2
Tx=
a , ()TTx
=
.
Распишем левую часть уравнение Лагранжа:
T
x
x
∂
=
∂
a ; 0
T
x
∂
=
∂
;
dT
x
dt x
∂
=
∂
a .
Определяем обобщенную силу по формуле:
()
k
A
Q
x
δ
δ
=
.
Тогда
1113333
cos sin
тр c
AF r F r P r M
δ
δγ δ δα δϕ
=⋅ − − ⋅ − .
При
gmP
33
= ,
11
sin
тр
FfmgfF
γ
=+ , αcosgkmM
33c
=
,
22
13 3
232
,,
22
rr
rxr x x
RrR
δ
δδ δδϕ δ
== = ,
будем иметь
2
13
23
(cos sin ) (sin cos )
2
rk
AF f fmgmg x
Rr
δ
γγ α αδ
⎡⎤
=−−− +
⎢⎥
⎣⎦
.
Окончательно
2
13
23
(
cos sin
)(
sin cos
)
2
rk
QF f fmgmg
Rr
γ
γαα
=−−− +
.
Тогда получим
x
Q=
a , откуда
Q
x
=
a
,
13
3
1
22
22
12 3
22
22
(cos sin ) (sin cos )
3
8
k
Fffmgmg
r
r
mm m
RR
γ
γαα
ρ
−−− +
=
++
a
.

271
Задача Д.8. Дифференциальные уравнения
движения механической системы
в обобщенных координатах
(Уравнение Лагранжа второго рода)
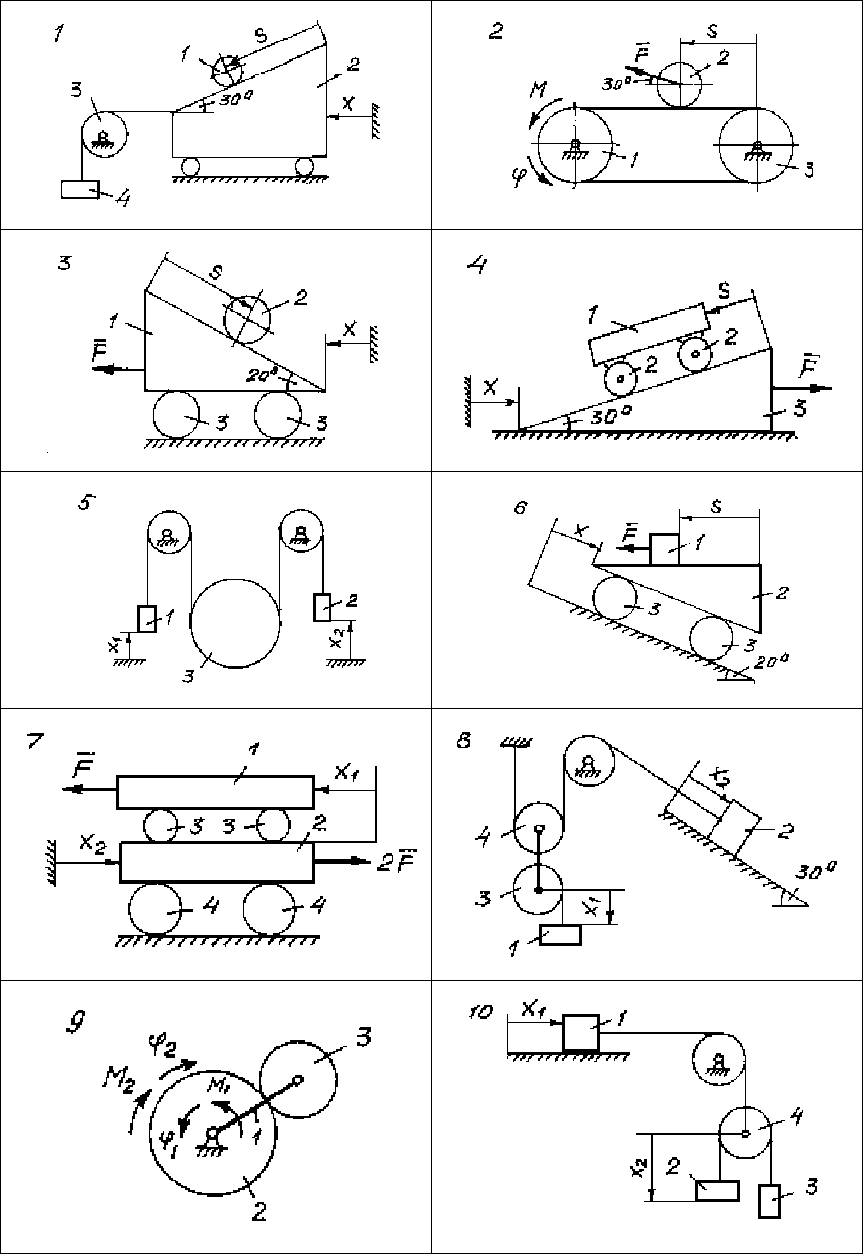
Механическая система (рис. 175 – 177) состоит из твердых тел и
нерастяжимых нитей. При движении тел трение скольжения отсут-
ствует. Заданная механическая система – голономная с двумя сте-
пенями свободы, имеет стационарные (склерономные) и двусто-
ронние связи. В вариантах встречаются следующие обобщенные
координаты:
s = s(t); x = x(t);
ϕ
=
ϕ
(t);
ϕ
1
=
ϕ
1
(t);
ϕ
2
=
ϕ
2
(t);
x
1
= x
1
(t); x
2
= x
2
(t).
Используя уравнения Лагранжа второго рода, определить уско-
рение тех тел, обобщенные координаты которых заданы. В вариан-
тах 9, 20, 22, 30 механизмы расположены в горизонтальной плоско-
сти. Все данные для расчета приведены в таблице 16.
Пример решения задачи
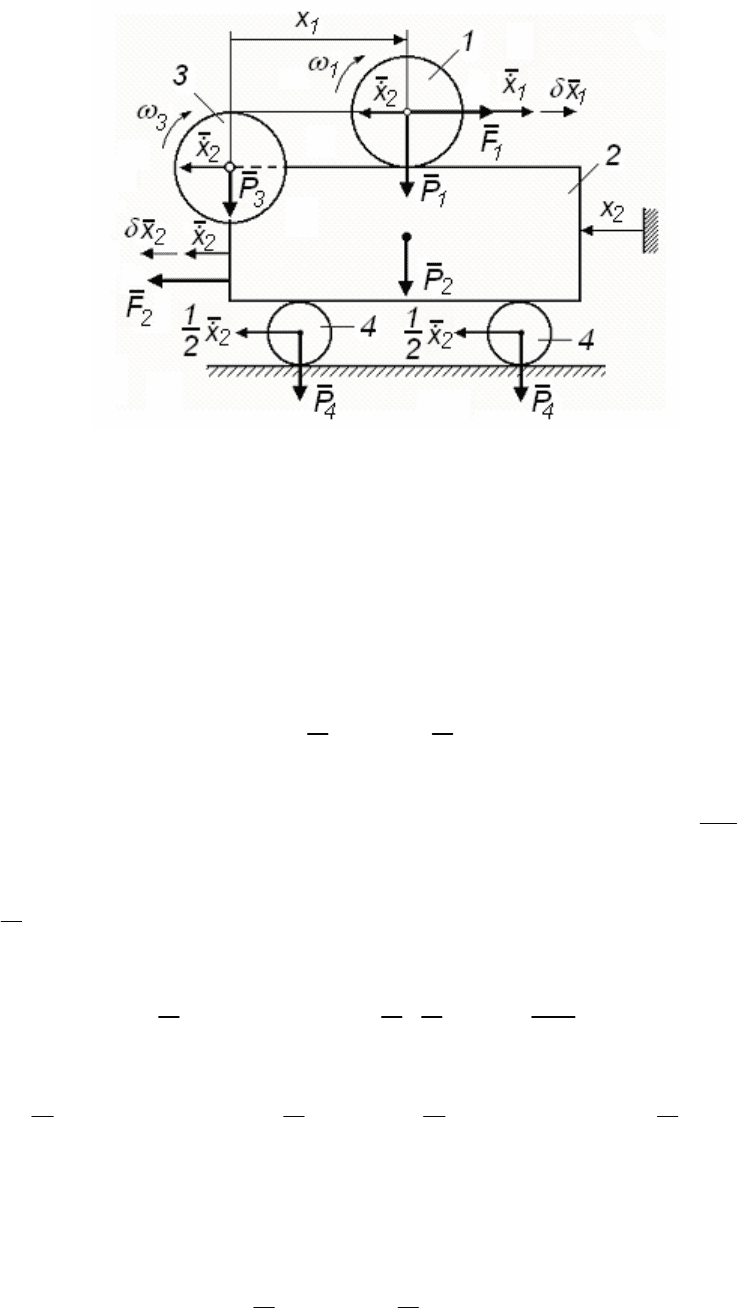
Голономная механическая система (рис. 178) состоит из твер-
дых тел (1 – 4) и нерастяжимой нити между телами 1 и 3. Система
движется под действием сил
1
F и
2
F . Обобщенные координаты x
1
,
x
2
показаны на чертеже. Заданы следующие величины: m
1
= 4 кг;
m
2
= 8 кг; m
3
= 2 кг; m
4
= 6 кг – массы тел; F
1
= 10 Н; F
2
= 40 Н –
действующие силы. Диск 1 и цилиндры 4 катятся без скольжения.
Определить ускорение центра масс тела 1 и тела 2.
Решение
На рис. 178 показываем скорости всех тел, входящих в систему,
выражая их через обобщенные скорости
1
x
и
2
x
.
272
Рис. 175
273
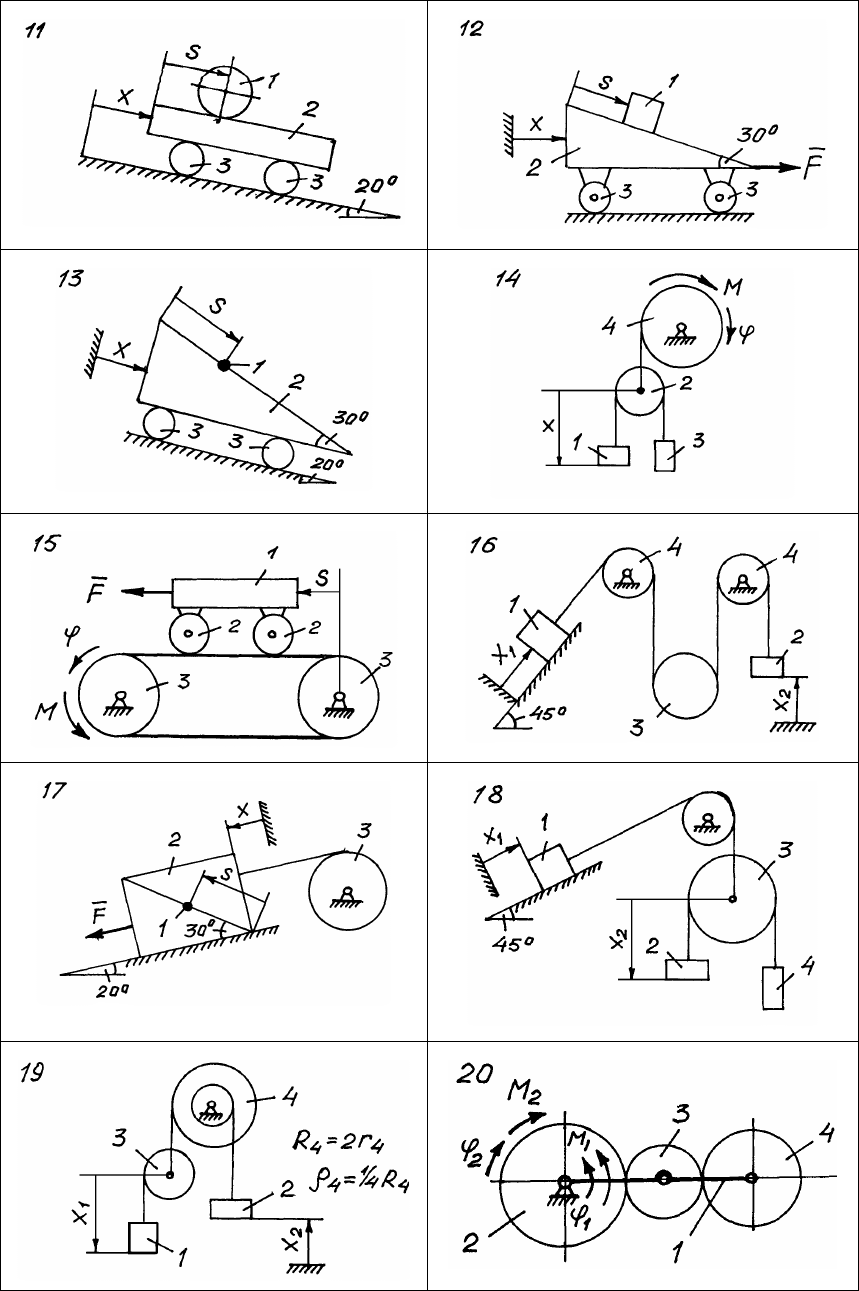
Рис. 176
274
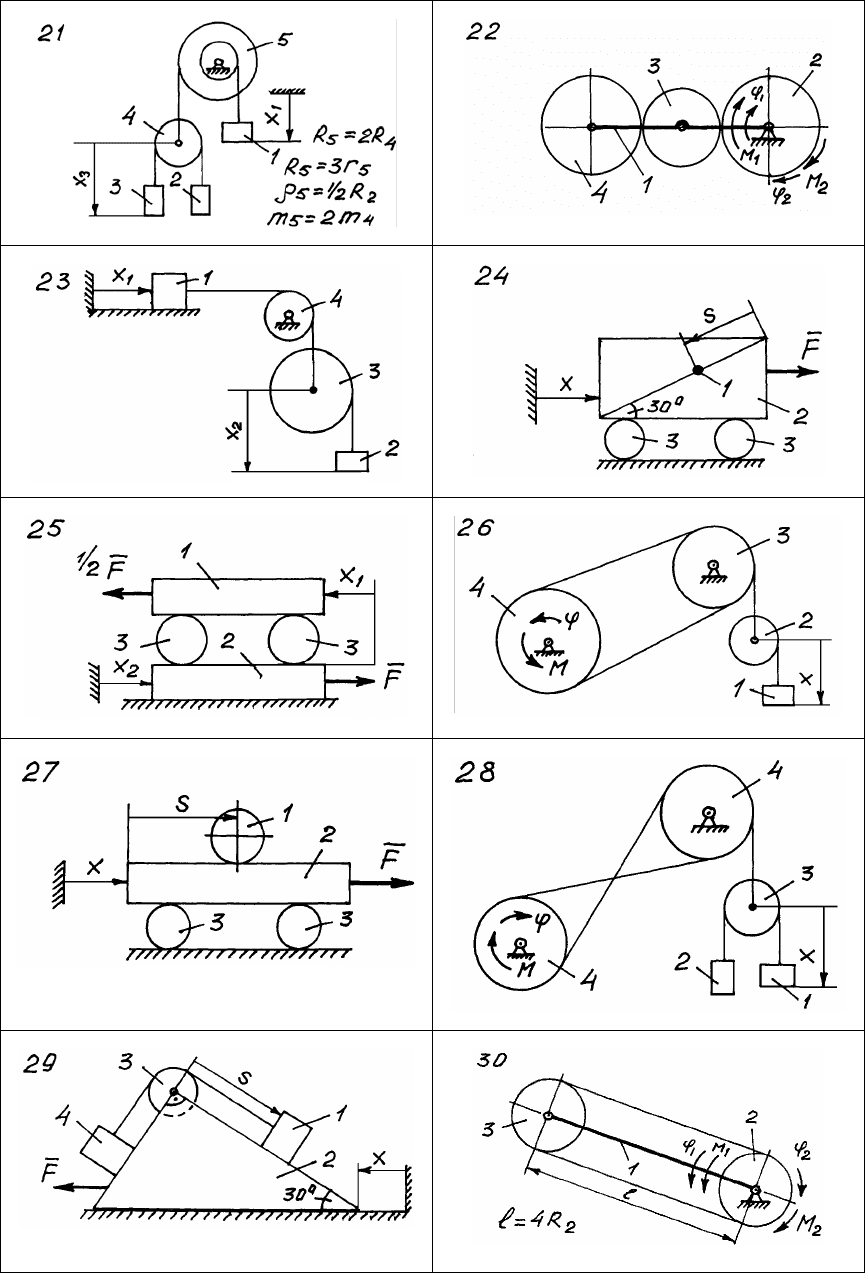
Рис. 177
275
Таблица 16
m
1
m
2
m
3
m
4
F
M
M
1
M
2
R
1
R
2
R
3
R
4
Номер
варианта
(рис.175-
177)
кг кг кг кг Н Нм Нм Нм м м м м
1
4 8 2 3 - - - - - - - -
2
10 6 10 - 6 2 - - 0,8 - 0,8 -
3
8 4 6 - 4 - - - - - - -
4
10 6 12 - 7 - - - - - - -
5
6 4 10 - - - - - - - 0,6 -
6
6 10 4 - 6 - - - - - - -
7
10 12 6 8 2 - - - - - - -
8
6 8 4 4 - - - - - - - -
9
8 9 6 - - - 2 3 1,2 - 0.4 -
10
10 8 4 6 - - - - - - - -
11
4 6 2 - - - - - - - - -
12
6 8 2 - 4 - - - - - - -
13
2 4 2 - - - - - - - - -
14
4 6 8 10 - 2 - - - - - 0,5
15
4 2 6 - 5 4 - - - - 0,6 -
16
2 4 6 5 - - - - - - - -
17
4 8 6 - 6 - - - - - - -
18
3 6 8 10 - - - - - - - -
19
2 4 6 10 - - - - - - - 0,8
20
6 8 4 2 - - 8 4 - 0,8 0,6 0,5
21
2 4 2 6 - - - - - - - 0,4
22
4 8 3 6 - - 2 6 - 0,8 0,4 0,6
23
5 6 8 2 - - - - - - - -
24
3 8 4 - - - - - - - - -
25
6 8 4 - 6 - - - - - - -
26
2 4 6 8 - 8 - - - - - -
27
4 8 2 - 4 - - - - - - -
28
4 2 6 8 - 12 - - - - - 0,8
29
8 10 4 2 5 - - - - - - -
30
4 6 6 - - - 8 2 - 0,6 0,6 -
276
Рис. 178
Вычисляем кинетическую энергию системы.
123 4
1
2
n
k
k
TTTTTT
=
==+++
∑
.
Тело 1 совершает плоское движение, поэтому
22
11111
11
22
Tmv
ω
=+
I
.
Абсолютная скорость
112
vxx=−
, угловая скорость
1
1
1
x
R
ω
=
,
2
111
1
2
mR=I - момент инерции тела 1.
Тогда
2
2
2
1
1112 11
2
1
111
()
222
x
Tmxx mR
R
=−+⋅ =
22
22
11 112 12 1 12 2
3131
44 4
4242
mx mxx mx x xx x=−+ =⋅−+⋅
;
2
2
11 122
34 2Tx xx x=− +
.
Тело 2 совершает поступательное движение, поэтому
22
222 22
11
84
22
Tmx xx==⋅=
277
2
22
4Tx=
.
Тело 3 совершает плоское движение, поэтому
2
2
332331
11
22
Tmx
ω
=+
I
.
При
1
3
3
x
R
ω
=
и
2
333
1
2
mR=
I , находим
222
222
332 31 2 12 1
11111
22 0,5
22224
Tmx mx x xx x=+⋅=⋅+⋅=+
;
2
2
32 1
0,5Tx x=+
.
Тело 4 совершает плоское движение, поэтому для однородных
цилиндров кинетическая энергия
3
4
2
444
T= mv.
При
44
1
v= x
2
, получаем
22
442 2
33
T= mx= 6x
16 16
⋅
.
2
42
T =1,125x
.
Окончательно запишем значение кинетической энергии системы в
следующем виде:
22
112 2
T = 3,5x - 4x x + 9,25x
.
Для обобщенных координат x
1
и x
2
запишем уравнения Лагран-
жа второго рода:
1
11
dT T
Q
dt x x
∂
∂
−
=
∂∂
;
2
22
dT T
Q
dt x x
∂
∂
−
=
∂∂
.
Кинетическая энергия
12
(, )TTxx
=
- функция только обобщен-
ных скоростей, поэтому
278
12
0
TT
xx
∂
∂
=
=
∂∂
.
Частные производные по обобщенным скоростям
1
x
и
2
x
:
12
1
74
T
x
x
x
∂
=−
∂
;
12
2
T
= 4x 18,5x
x
∂
−+
∂
.
Полученные выражения дифференцируем по времени:
12
1
74
dT
x
x
dt x
⎛⎞
∂
=−
⎜⎟
∂
⎝⎠
;
12
2
dT
= -4x +18,5x
dt x
⎛⎞
⎜⎟
⎝⎠
∂
∂
.
На схеме рис. 177 показываем возможные перемещения цен-
тров масс тел 1 и 2.
Вычисляем обобщенные силы.
Обобщенная сила
1
1
1
()
k
A
Q
x
δ
δ
= , при этом
δ
x
1
≠
0,
δ
x
2
= 0.
111
()
k
AFx
δ
δ
= , тогда
11
QF10кН
=
=
.
Обобщенная сила
2
2
2
()
k
A
Q
x
δ
δ
=
, при этом
δ
x
2
≠
0,
δ
x
1
= 0.
k2 2 2 1 2 2 1 2
(
δA
)
=F δx-Fδx=
(
F-F
)
δx . Тогда
22
QF30кН
=
=
.
При
11
x =
a (относительное ускорение тела 1) и
22
x =
a , окон-
чательно запишем систему двух алгебраических уравнений:
-
+
74 10;
-4 18,5 = 30.
12
12
=
⎧
⎨
⎩
aa
aa
Определитель коэффициентов при неизвестных
a
1
и
a
2
7-4
∆
= =129,5 -16 =113,5
-4 18,5
.
279
1
10 -4
∆
= = 185 +120 = 305
30 18,5
;
==+=
−
710
∆
210 40 250
2
430
.
Тогда
2
1
1
∆
305
2,7
∆ 113,5
м/с== ≅a ;
2
2
∆
250
2, 2
∆ 113,5
2
м/с== ≅a .
Окончательный ответ: a
1
= 2,7 м/с
2
; a
2
= 2,2 м/с
2
.
