Теоретическая механика - теория, задания и примеры решения задач

Подождите немного. Документ загружается.

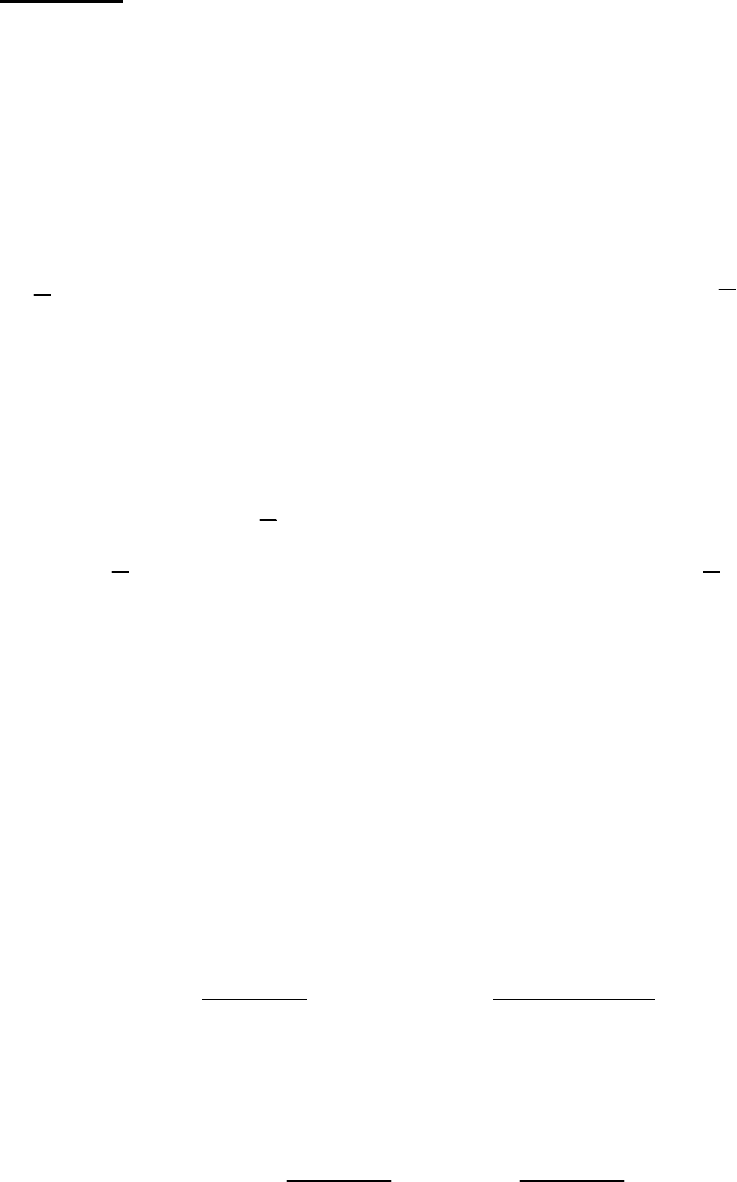
240

Требуется определить момент M, если P = Q = 0,5 Н, а = 1 м.

Решение

Так как связи идеальные и удерживающие, то применяем прин-

цип возможных перемещений

∑

Сообщаем точкам системы возможные перемещения. Так как

все связи стационарные (склерономные), то возможные перемеще-

ния

удовлетворяют тем же условиям, что и скорости

V .

Звенья OA и O

D могут совершать вращательные движения,

звенья ABD и BC – плоскопараллельное, а ползун C - поступатель-

ное.

Сообщим звену OA бесконечно малый поворот под углом

тогда перемещение

будет перпендикулярно звену OA, пере-

мещение

- перпендикулярно O

D, перемещение

- парал-

лельно направляющей плоскости ползуна.

Строим мгновенный центр поворотов звеньев ABD, BC.

Запишем сумму работ момента M и сил P, Q на собственных

возможных перемещениях:

cos60 cos30 0.

MPr Qr

δϕ δ δ

−− + =

(4)

Определим все возможные перемещения через

; cos60 ; cos60 cos30 .

AABCB

rrrrr

δδϕδδ δ δ

== =

DDD

Тогда

()

cos30

cos 60

cos60

δϕ δϕ

δδ

Полученные перемещения подставим в (4), тогда будем иметь:

cos60 cos30

cos60 cos60

MP Q

δϕ δϕ δϕ

⎛⎞

−− + =

⎜⎟

⎝⎠

241

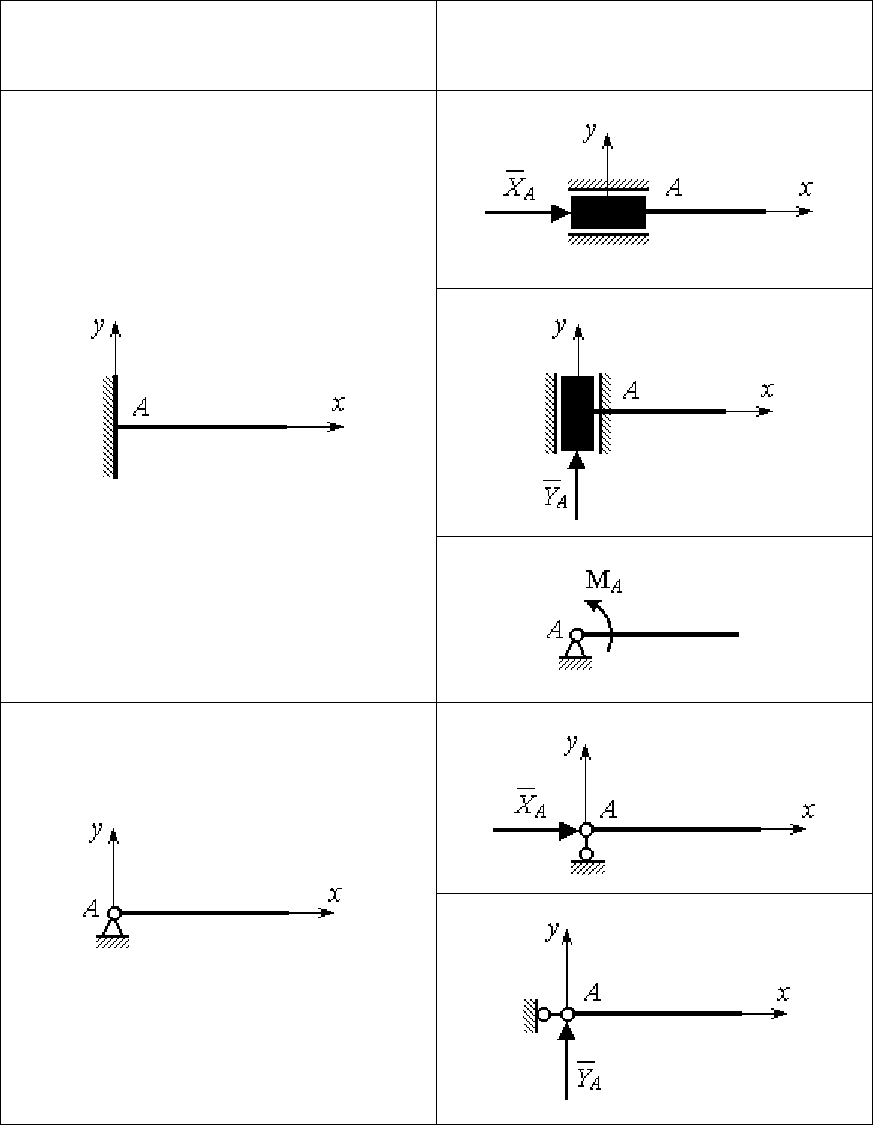
Таблица 15

Заданная схема опоры

Эквивалентно – расчетная

схема

Плоская жесткая заделка

Неподвижный цилиндрический

шарнир

242

При

≠

, окончательно получим

(3 ) (3 0,5 0,5) 1 1 .MQP Нм=−=⋅−⋅=a

Ответ: 1.M Нм=

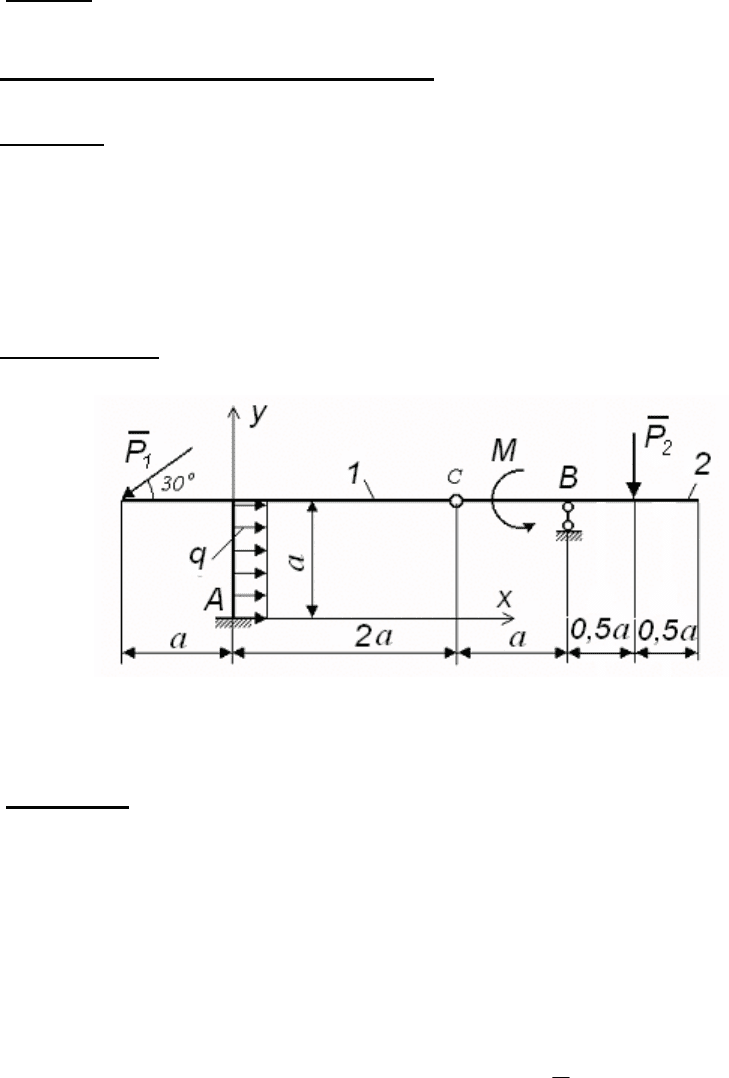
Пример решения задачи Д. 5.2

Задана плоская (рис. 156) неподвижная конструкция, которая со-

стоит из двух тел 1 и 2, соединенных между собой шарниром C. На

раму 1 действует сосредоточенная сила P

= 10 кН и равномерно

распределенная нагрузка q = 2 кН/м, а на балку 2 – пара сил с мо-

ментом M = 6 кНм и сосредоточенная сила P

= 8 кН.

Определить

реакции опор A и B, если a = 2 м.

Рис. 156

Решение

1. Определение момента пары в заделке A (M

Вместо заданной жесткой заделки A показываем эквивалентно-

расчетную схему (неподвижный цилиндрический шарнир A и мо-

мент M

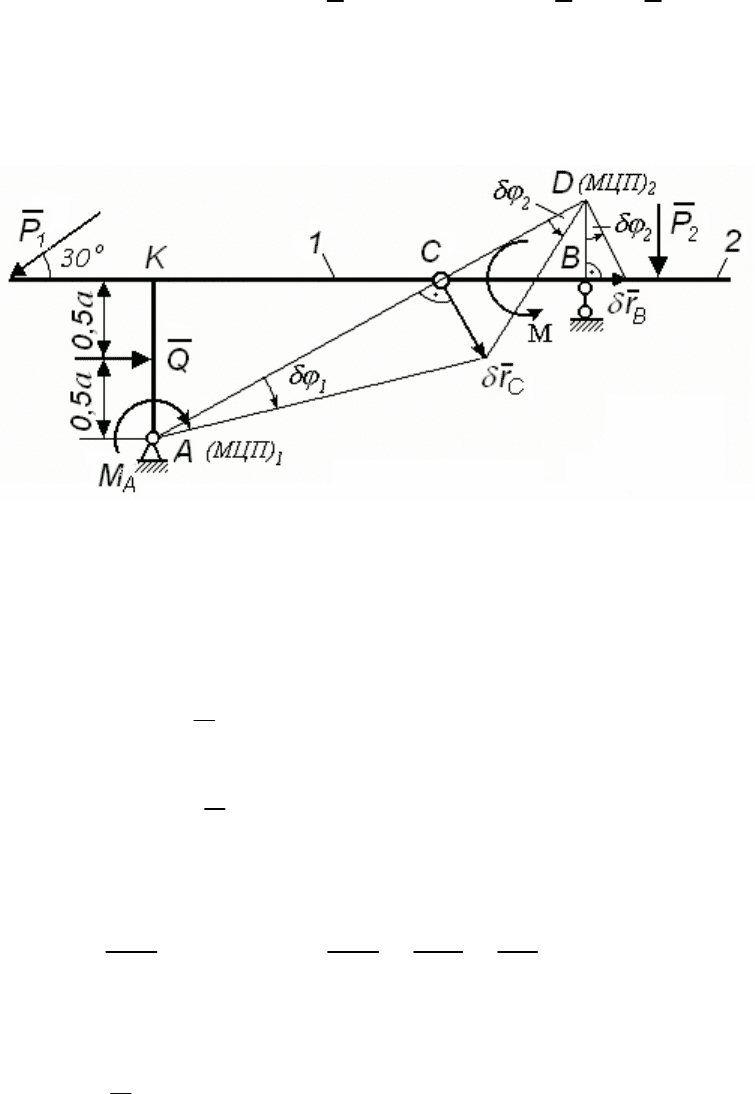
) (рис. 157). Тогда вся конструкция становится механизмом.

Рама 1 может вращаться вокруг шарнира A, поэтому эта точка и

будет (МЦП)

для рамы. Точку A соединяем с точкой C и показыва-

ем возможное ее перемещение

rAC

⊥

. При этом

rAC

δϕ

=⋅, где

- возможный угол поворота рамы 1.

243

Определим МЦП для балки 2. Опора B позволяет точке B пере-

мещаться по горизонтали -

. К векторам

восстанав-

ливаем перпендикуляры. Их пересечение дает точку D – (МЦП)

балки 2, а

- возможный угол поворота.

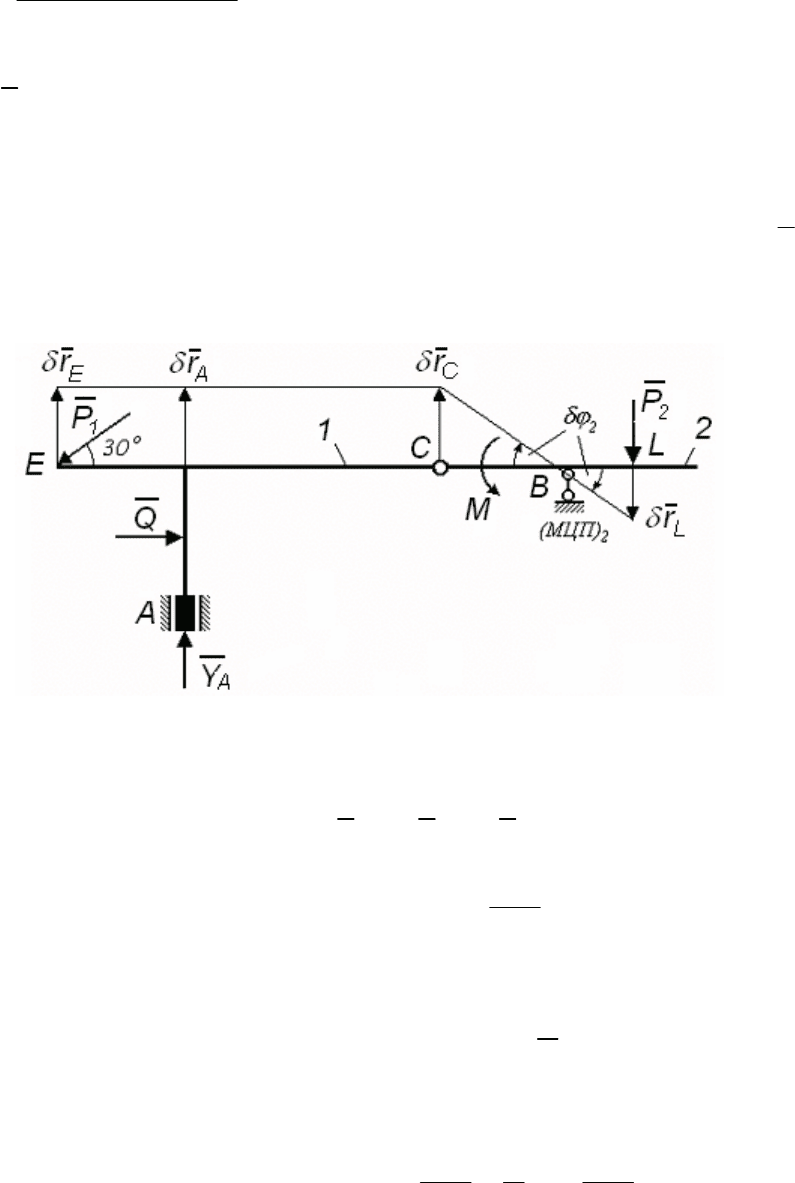
Рис. 157

Составим уравнение работ (3) моментов сил относительно со-

ответствующих МЦП.

111 11 1

cos30 sin30

MQ P P

ϕδϕ δϕ δϕ

−−+aa a

22 2

δϕ δϕ

+− =a (5)

Для рамы 1

rAC

δϕ

=⋅; для балки 2

rCD

δϕ

=⋅.

Тогда

ϕδϕ

= . Так как

AC KC

CD CB

, то

ϕδϕ

= .

При

≠ уравнение (5) запишем в виде:

(cos30 sin30 ) 2 0.

MQP MP+− + +−=aa a

Из него, при

22 4Qq==⋅=a кН, находим

= P

a(cos30 sin30

) + P

a – 1/2Qa – 2M =

=10

⋅

2(0,866 + 0,5) + 8

⋅

2 – 1/2

⋅

2 - 2

⋅

6 = 27,32 кНм.

244

Итак,

M27,32кНм=

2. Определение вертикальной составляющей реакции в задел-

ке A (

Теперь точку A представим в виде ползуна, который может

вместе с рамой 1 перемещаться поступательно по вертикали в

своих направляющих (рис. 158). К ползуну прикладываем силу

Y .

Тогда вся конструкция становится механизмом.

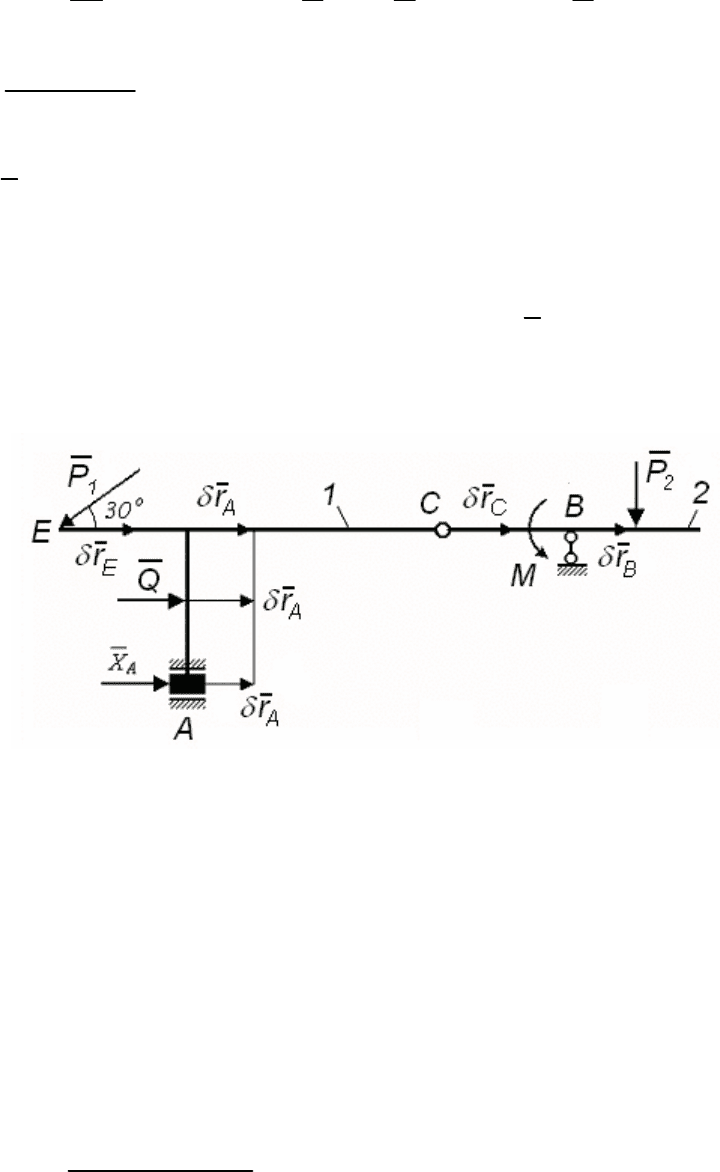
Рис. 158

При поступательном перемещении рамы 1 возможные перемеще-

ния точек E, A и C равны, т.е.

EAC

rrr

δδ

. (МЦП)

балки 2 бу-

дет находиться на опоре B, поэтому

δϕ

. Запишем уравне-

ние работ

1222

cos60 0

EAA

Pr Y r M P

δ δ δϕ δϕ

−+−+=a .

Все возможные перемещения точек выразим через

cos60 0

CAC

Pr Y r M P

δδ

−+−+=a

При

≠ , определим Y

245

16 1

cos60 10 0,5 8 4

22 2

YP P=+ − =+⋅ −⋅=

кН.

Итак,

Y кН=

3. Определение горизонтальной составляющей реакции в задел-

ке A

()

Вместо заделки в точке A показываем ползун (рис. 159), который

может перемещаться поступательно вместе с рамой 1 в своих на-

правляющих. К ползуну прикладываем силу

, теперь вся конст-

рукция становится механизмом.

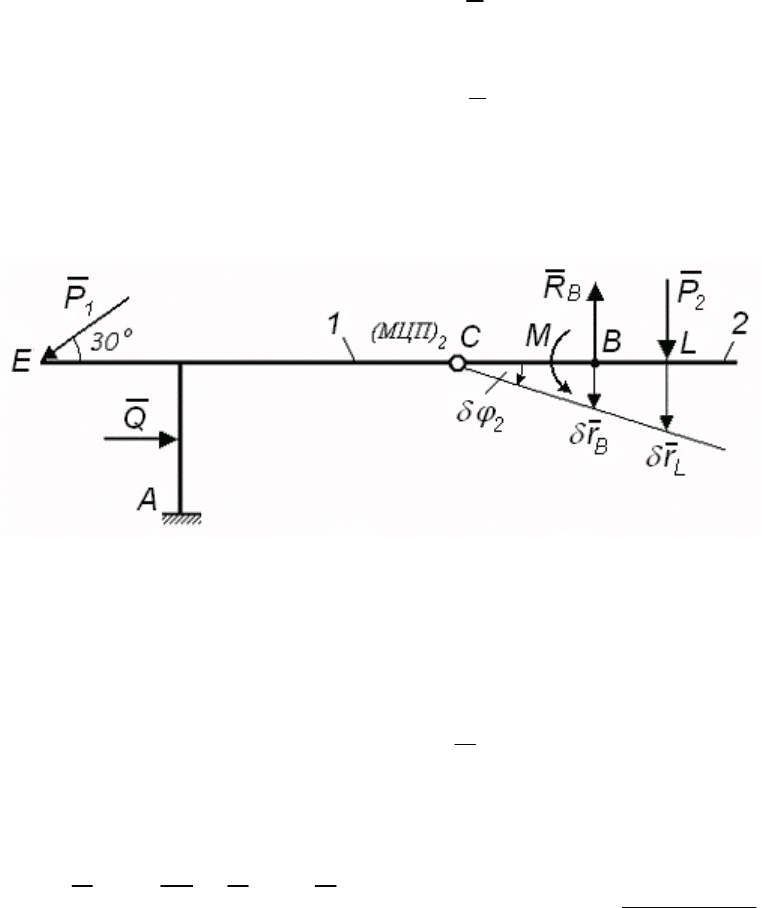
Рис. 159

При поступательном перемещении рамы 1 балка 2 тоже будет

перемещаться поступательно, опора B это допускает.

Составляем уравнение работ всех сил

cos30 0

EAAA

Pr Qr X r

δδδ

−

++ =.

При

=≠ находим

cos30 10 0,866 4 4,66

XP Q=−=⋅−= кН.

Итак,

4, 66

X кН

246

4. Определение реакции в опоре B (

Опора B – подвижный цилиндрический шарнир. Мысленно убираем

опору B и показываем вектор реакции

R , который будет перпен-

дикулярен к балке 2. Теперь рама 1 неподвижна, а балка 2 может

вращаться относительно шарнира точки C (рис. 160).

Рис. 160

Точка C будет (МЦП)

балки 2,

- возможный угол поворота.

Составим уравнение работ моментов сил относительно (МЦП)

2222

MR P

δϕ δϕ δϕ

−− + =aa.

При

≠ , определяем

R :

336

222

RP=−=⋅−=

кН. Итак,

R кН=

Все реакции в опорах конструкции найдены.

5. Проверка правильности полученных результатов.

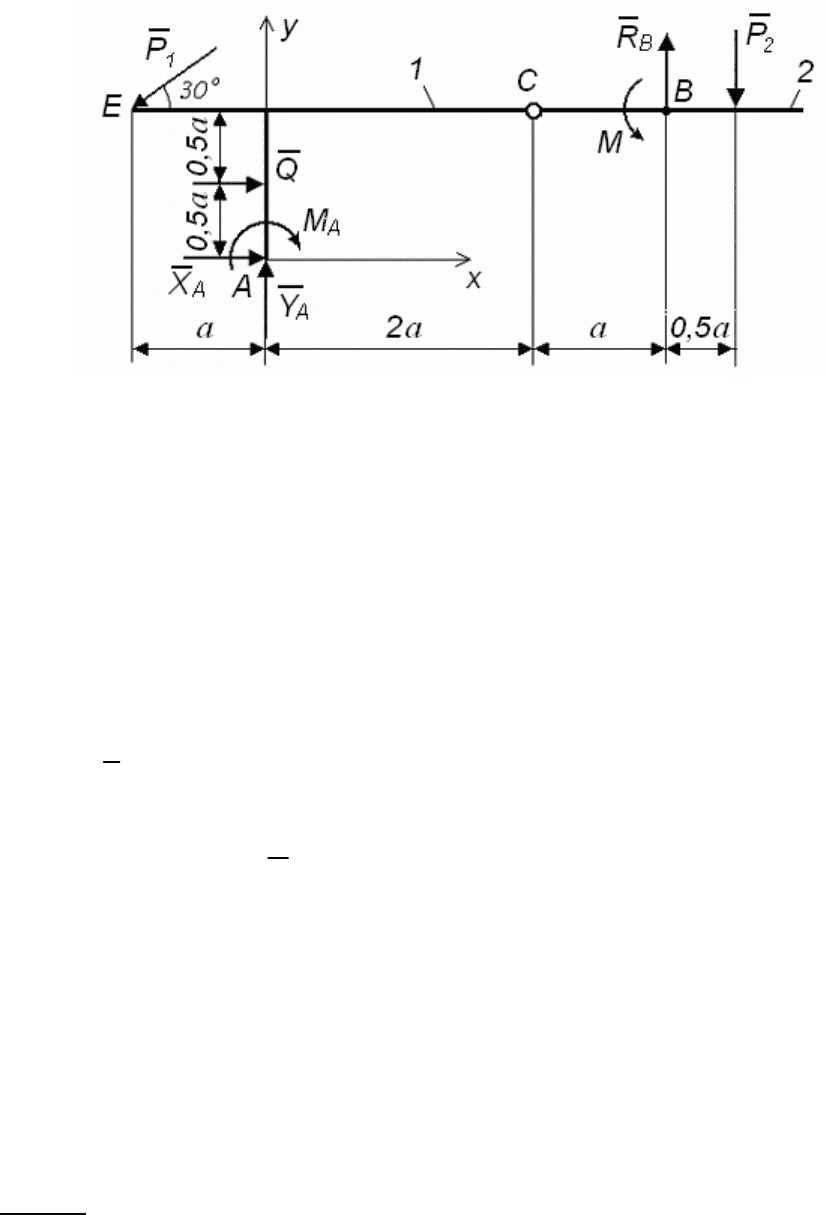
Изображаем всю конструкцию и показываем действующие (за-

данные) силы и реакции опор (рис. 161).

Для проверки используем уравнения статики. Если все реакции

опор найдены верно, то применяя уравнения статики должны полу-

чить тождество (0 ≡ 0).

247

Рис. 161

F =

∑

;

cos30 0

XQP+− =; 4,66 4 10 0,866 0

−⋅ =; 0 ≡ 0.

F =

∑

;

cos60 0

YP RP−+−=; 4100,598 0

−

⋅+−=; 0 ≡ 0.

()

MF=

∑

;

cos60 3 2

AAA B

PQXMYMR⋅+⋅ + ⋅− −⋅++ ⋅−aaa a a

1, 5 0 ;P−⋅ =a

10 0,5 3 2 4 0, 5 2 4, 66 2 27,32 4 2 2 6 9 2 8 1,5 2 0⋅⋅⋅+⋅⋅+ ⋅− −⋅⋅++⋅−⋅⋅=

;

67,32 67,32 0−=; 0 ≡ 0.

Все реакции найдены верно.

Ответ: M

= 27,32 кНм; X

= 4,66 кН; Y

= 4 кН; R

= 9 кН.

248

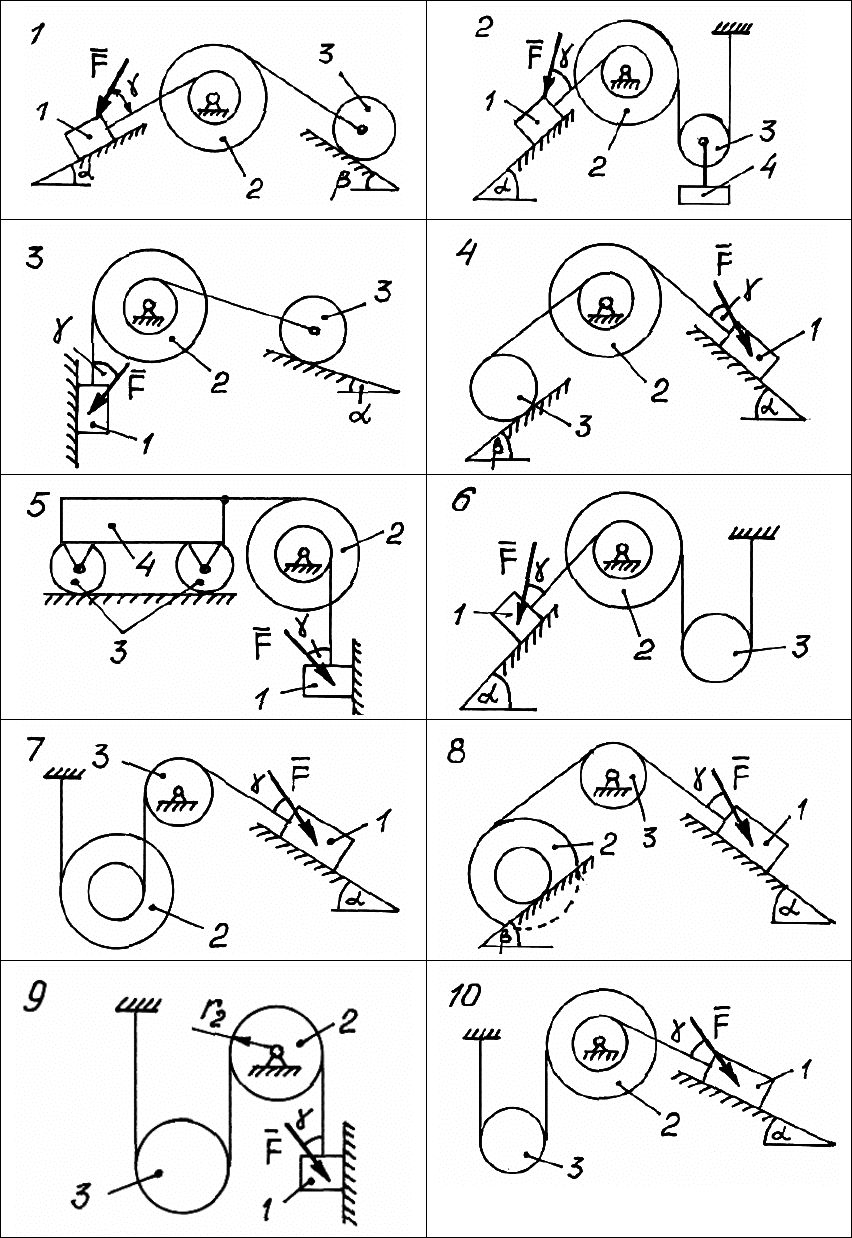
Задача Д.6. Общее уравнение динамики

На рис. 163 – 165 показаны механические системы с одной сте-

пенью свободы, которые состоят из твердых тел, соединенных не-

весомыми и нерастяжимыми нитями.

Заданы следующие параметры:

4321

m,m,m,m - массы соот-

ветствующих тел;

F - активная сила, приложенная к телу 1;

223

,,rRr - радиусы колес (

R - наибольший радиус колеса 2);

ρ -

радиус инерции тела 2;

- коэффициент трения скольжения тела

k - коэффициент трения качения тел;

βγ

- углы наклона

плоскостей к горизонту и силы

F к опорной поверхности тела 1.

Каток считать однородным цилиндром.

Используя общее уравнение динамики, определить ускорение

тела 1

()a .

1. Принцип Даламбера

1.1 Материальная точка

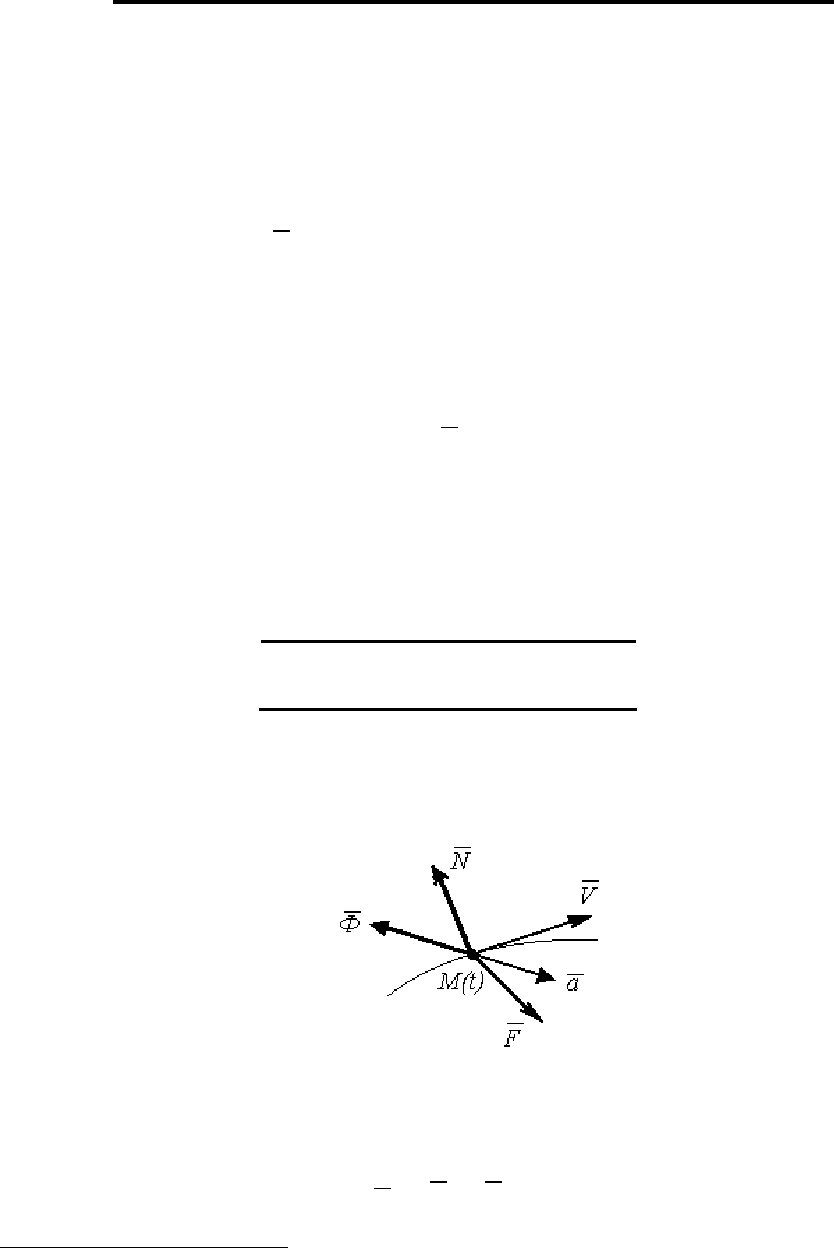
Рассмотрим (рис. 162) несвободное движение точки по задан-

ной траектории в произвольный момент времени.

Рис. 162

Запишем для точки M основное уравнение динамики:

mFN

+a ; (1)

Даламбер Жан Лерон (16.9.1717 – 29.10.1783). Французский математик, ме-

ханик, философ, член французской АН с 1754 г. Исследования относятся к ме-

ханике, гидродинамике, математике.

249

Рис. 163