Теоретическая механика - теория, задания и примеры решения задач
Подождите немного. Документ загружается.

220
Тогда первое уравнение будет иметь вид:
15
8 80cos20 19 78,4 sin30
oo
T=−+ −a
, или
15
895,4T
=
−a
, где
11
x
=
a .
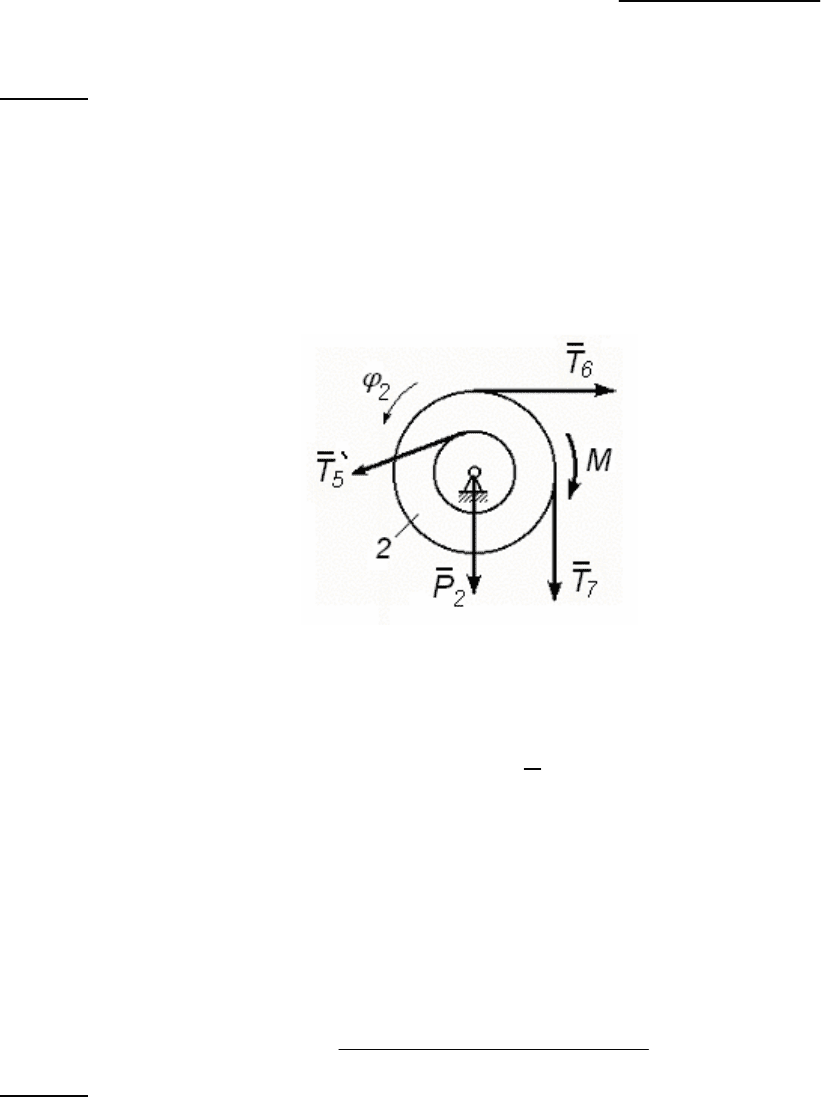
Тело 2
Двухступенчатый шкив 2 вращается (рис. 139) вокруг горизон-
тальной оси.
На тело 2 действуют следующие силы:
P
2
= m
2
g = 10
⋅
9,8 = 98 Н
– сила тяжести тела;
T
5
= T
5
', T
6
, T
7
– силы натяжения нитей; M –
пара сил.
Рис. 139
Для тела 2 применяем дифференциальное уравнение (6):
22
()
;
e
zzk
MF
ϕ
=
∑
I
где
22 2
222
10 0,6 3,6
z
m кгм
ρ
==⋅=I ;
22 1
2,5
ϕ
ε
=
=
a .
Тогда
'
152 67 2
3, 6 2,5 ( )Tr T T R⋅⋅=⋅−+⋅a
,
'
15 6 7
90,40,80,8TTT=⋅−⋅−⋅a .
Окончательно получаем
'
15 6 7
22,5 2 2TTT=− −a .
Тело 3
Диск 3 (рис. 140) находится в плоском движении.
На диск 3 действуют следующие силы:
P
3
= m
3
g= 4
⋅
9,8 = 39,2 Н
– сила тяжести диска;
T
7
, T
8
– силы натяжения нитей.

221
Рис. 140
Запишем дифференциальные уравнения (7) для диска:
3
33
33
;
();
e
kx
e
zzk
mx F
MF
ϕ
=
=
∑
∑
I
третье уравнение – тождество
00
≡
, так как
3
y const= и
3
0
e
ky
F =
∑
.
При
33 1
2x ==
aa и
33 1
5
ϕ
ε
==
a получим:
31 7 3 8
2
33 3 8 3
2;
1
.
2
mTPT
mR T R
ε
⋅=−−
⎧
⎪
⎨
⋅=⋅
⎪
⎩
a
Из второго уравнения находим
T
8
:
2
33 3
1
81
40,45
4
22
mR
T
ε
⋅
⋅⋅
== =
a
a
.
Из первого уравнения определим
T
7
:
73138 1 1
22439,24Tm PT
=
++=⋅ + +aaa,
или
71
39,2 12T =+a
.
222
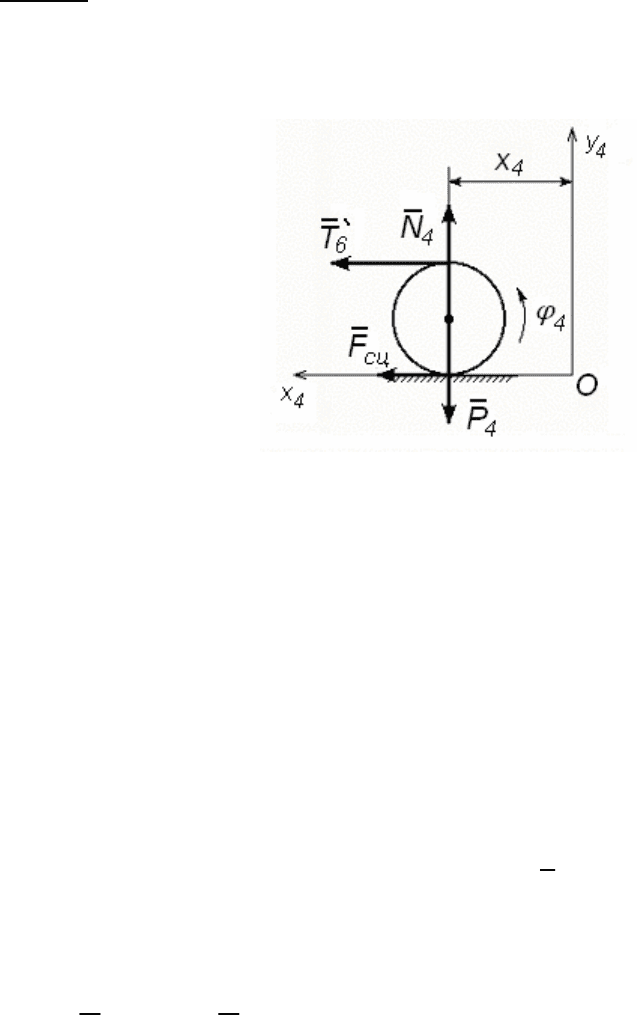
Тело 4
Цилиндр 4 (рис. 141) находится в плоском движении. Он катится
по горизонтальной плоскости без скольжения.
Рис. 141
На цилиндр действуют силы: P
4
= m
4
⋅
g = 6
⋅
9,8 = 58,8 Н – сила тяже-
сти цилиндра; N
4
– реакция нормального давления; F
сц
– сила тре-
ния сцепления; T
6
’
– сила натяжения нити (T
6
= T
6
’
).
Для цилиндра запишем дифференциальные уравнения (7):
4
e
44 kx
=;mx F
∑
.
4
e
44 ky
e
4z 4 z k
m
y
=F;
=M
(
F
)
ϕ
∑
∑
I
При
441
x ==
aa,
44 1
1, 6 7
ϕ
ε
==
a ,
44
y
R const
=
= ,
22
444
11
60,6 1,08
22
z
mR==⋅⋅=I (кгм
2
)
система уравнений принимает вид:
'
16
44
'
164 4
6;
0;
1, 0 8 1, 6 7 .
сц
сц
TF
NP
TR F R
=+
=−
⋅⋅=⋅−⋅
a
a
Откуда
44
58,8NP== Н;

223
16
16
6;
3.
сц
сц
TF
TF
′
=+
⎧
⎪
⎨
′
=−
⎪
⎩
a
a
В полученных уравнениях исключаем силу F
сц
и получим
61
4,5T
′
=
a .
Составим систему алгебраических уравнений, полученных для
каждого тела:
15
15 6 7
17
16
895,4;
22,5 2 2 ;
12 39,2 ;
4,5 ;
T
TTT
T
T
=−
⎧
⎪
′
=− −
⎪
⎨
+=
⎪
⎪
′
=
⎩
a
a
a
a
где
5566
;TTTT
′′
==.
Из последних уравнений находим
67 1
39,2 16,5TT
′
+= + a .
Первое и второе уравнения сложим
67 1
15,2 47,7TT−− = −a .
Получаем конечное уравнение
1
31,7 8,5 0
−
=a , откуда
1
8,5
0, 27
31,7
=≅
a м/с
2
.

224
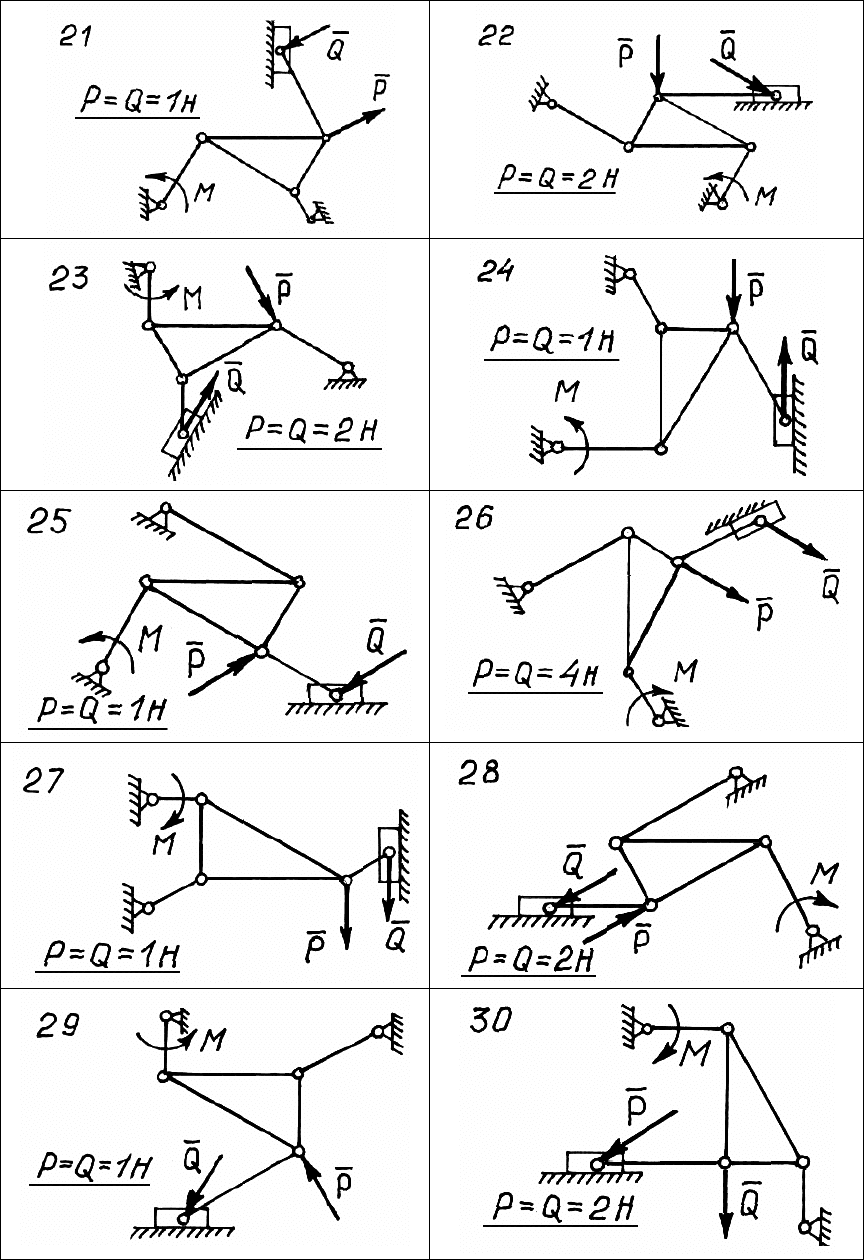
Задача Д.5. Принцип возможных перемещений
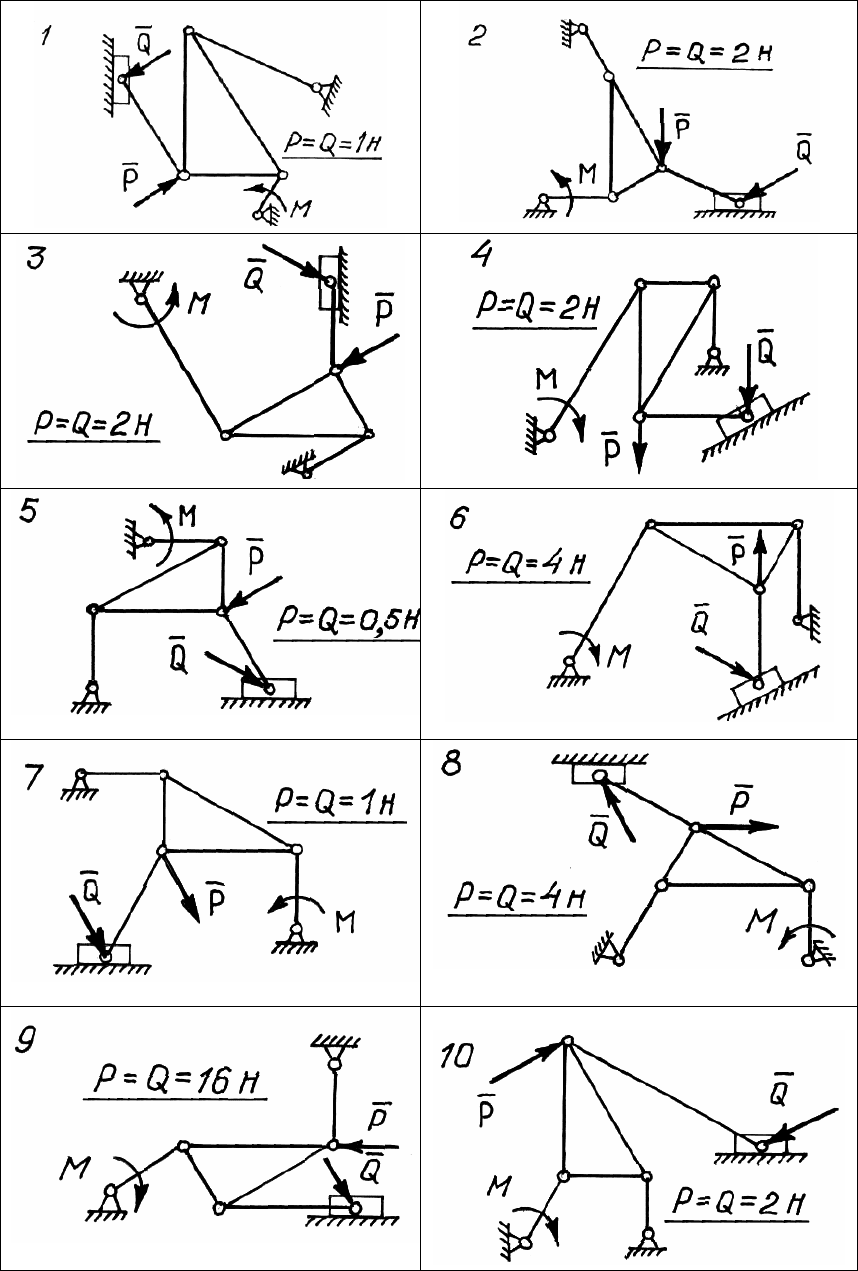
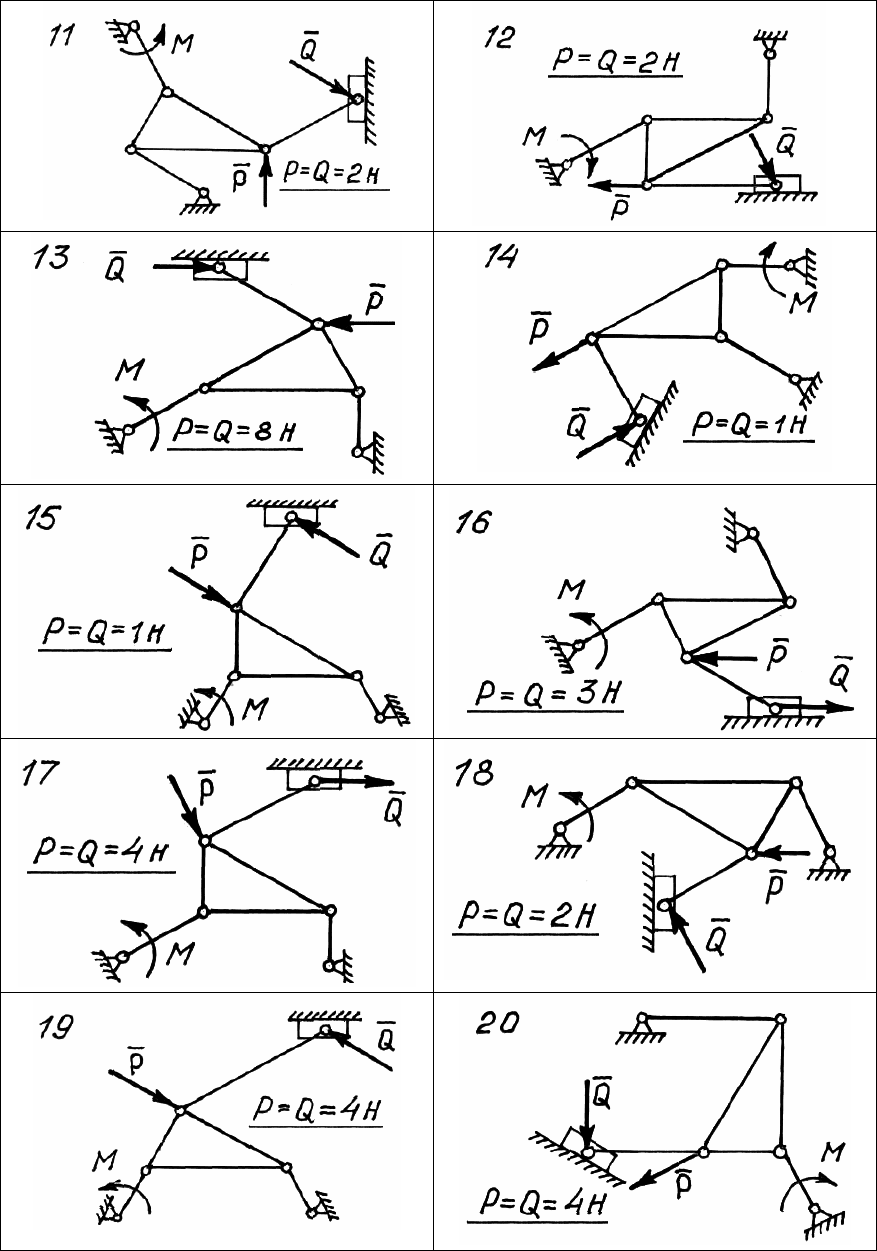
Д. 5.1. Равновесие плоского механизма
Плоский механизм (рис. 142 – 144) с идеальными и удержи-
вающими связями находится в равновесии под действием момента
M и сил P, Q.
Все силы, стержни и плоскость ползуна направлены под углами
0
О
, 30
О
, 60
О
, 90
О
к горизонту.
Определить момент M по заданным силам P и Q, если длина
кривошипа
а = 1 м.
Ответ: M = 1 Нм.
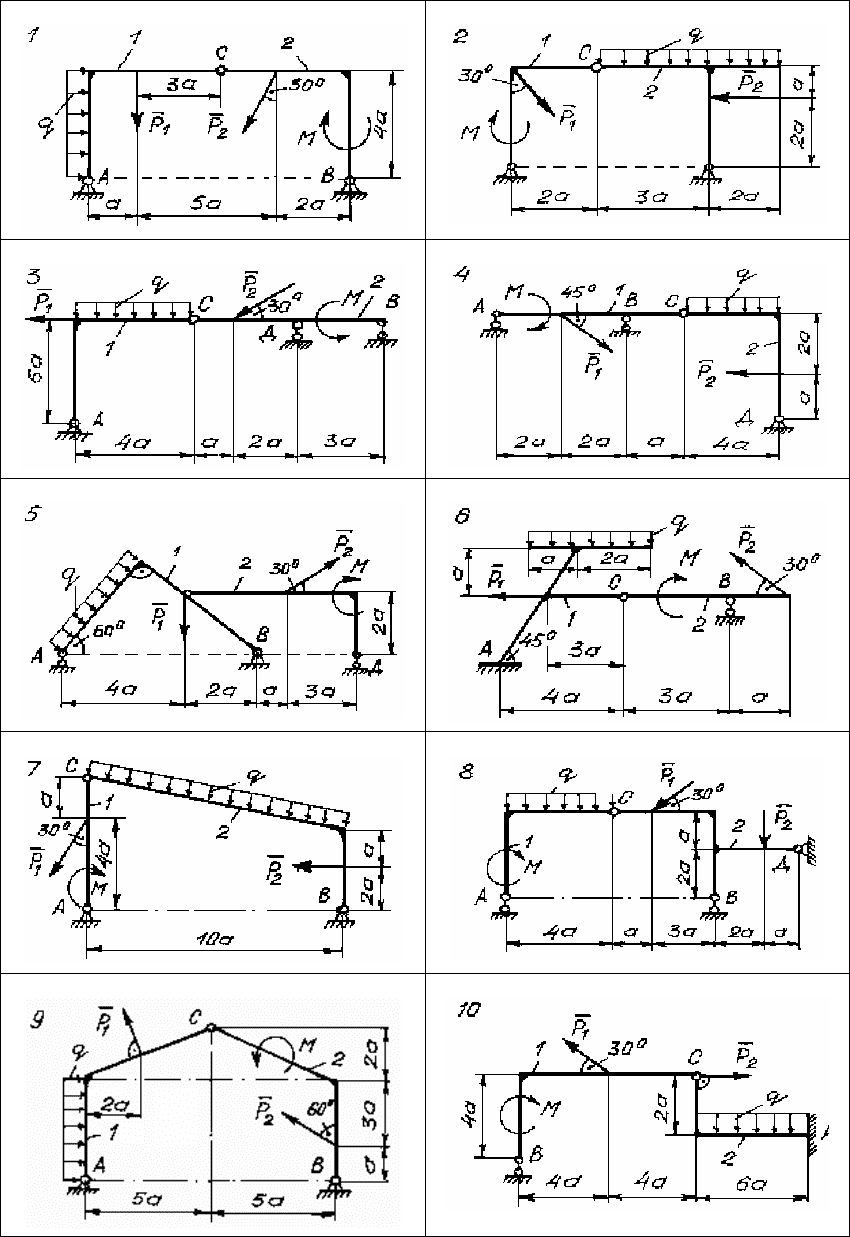
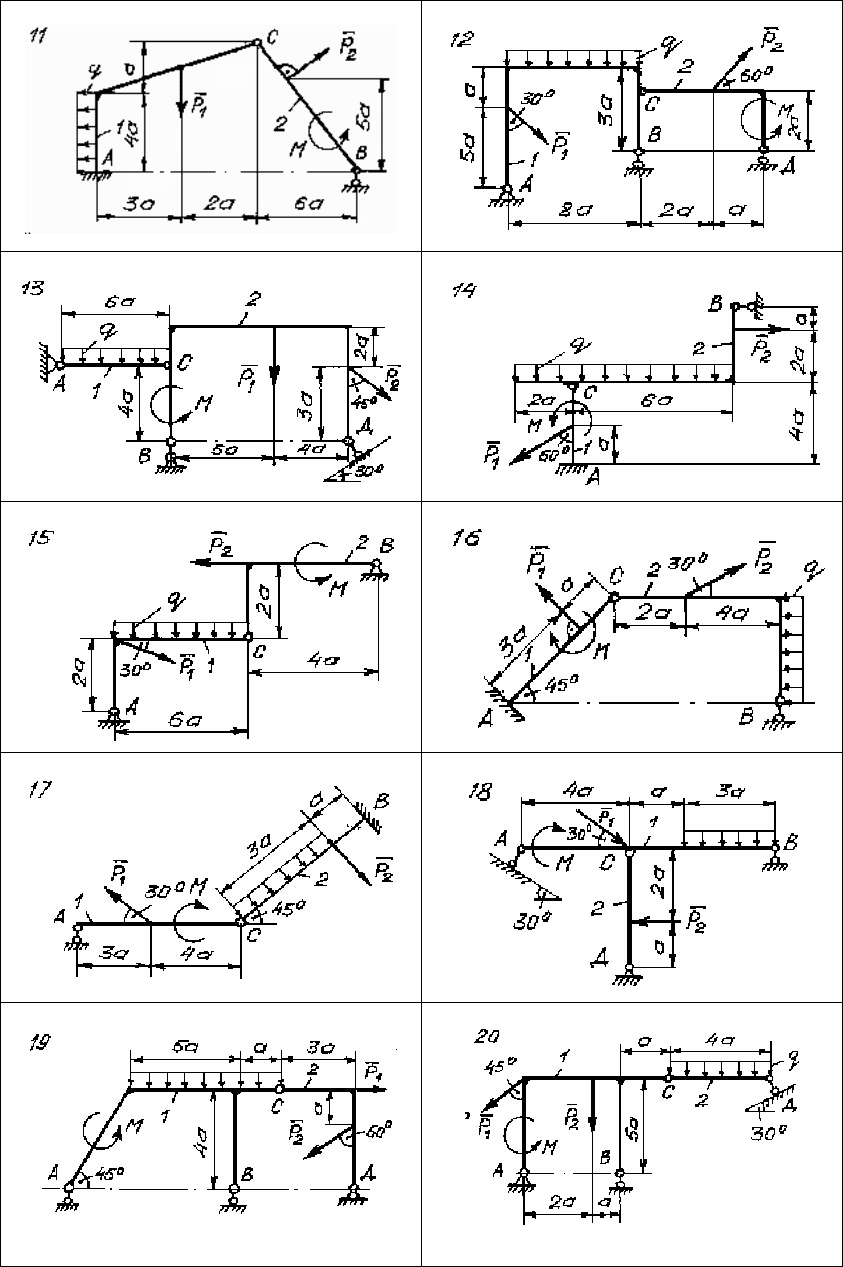
Д. 5.2. Определение реакций плоской конструкции
Задана плоская конструкция (рис. 145 – 147), состоящая из двух
тел 1 и 2, соединенных между собой при помощи цилиндрического
шарнира C. На конструкцию действуют: P
1
, P
2
– сосредоточенные
силы; M – момент пары сил; q – равномерно распределенная на-
грузка. Используя принцип возможных перемещений, определить
реакции в опорах A, B и D.
Необходимые для расчета данные приведены в таблице 14.
1. Классификация механических связей
Механические связи – это тела, которые ограничивают поло-
жение или движение точек механической системы
.
В аналитической механике, как и в статике, действует принцип
освобождаемости от связей. Несвободную механическую систему
формально можно представить свободной, если отбросить связи и
их действие на систему заменить реакциями связей.
Геометрическая связь налагает ограничение на координаты
точки. Уравнение такой связи имеет вид f(x; y; z; t; C) = 0;
225
Рис. 142
226
Рис. 143
227
Рис. 144
228
Рис. 145
229
Рис. 146
