Теоретическая механика - теория, задания и примеры решения задач
Подождите немного. Документ загружается.

190
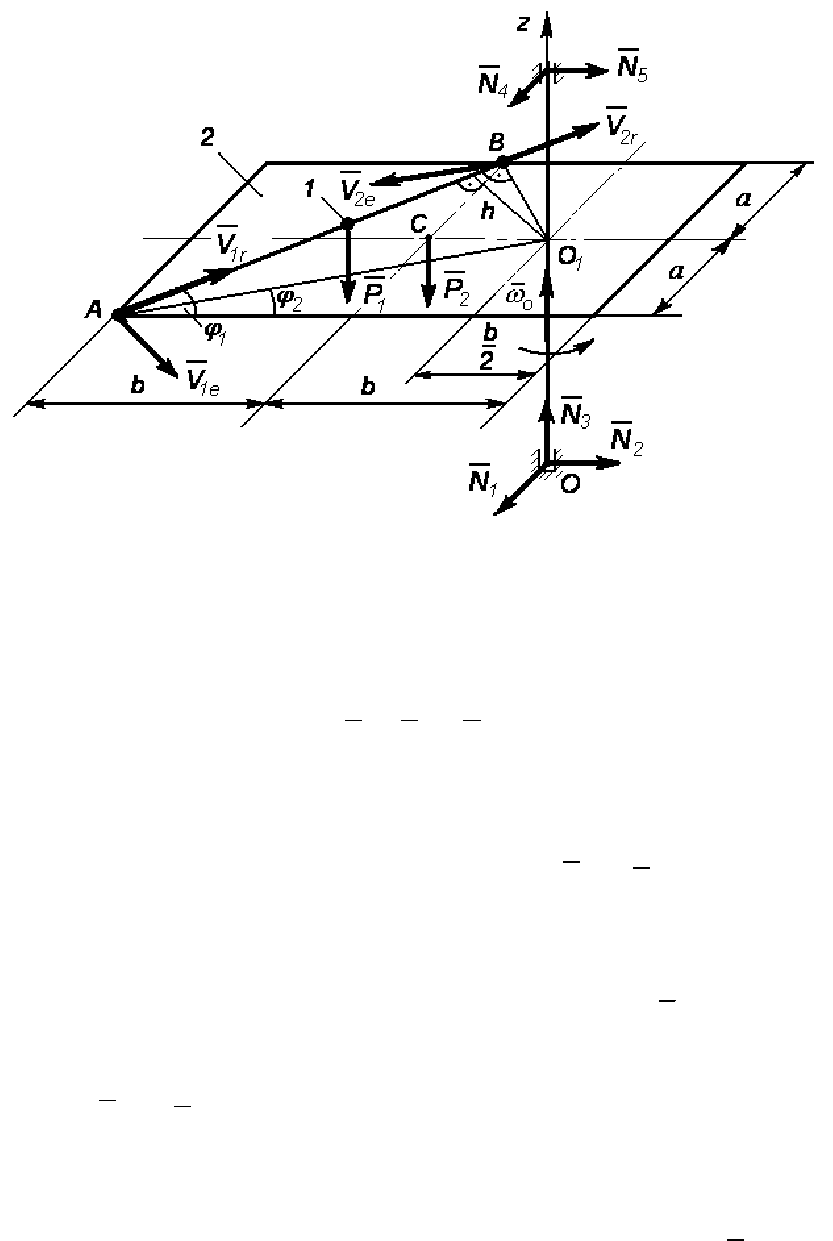
Рис. 122
Точка 1 совершает сложное движение, состоящее из переносно-
го и относительного движений. Поэтому
er
VV V
=
+ .
Покажем эти скорости на схеме. Обозначим точку пересечения
оси Oz с плоскостью пластины
O
1
. В начальный момент, когда точ-
ка находится в
A, относительная скорость
1r
Vu
=
направлена по
траектории от
A к B. Чтобы показать переносную скорость, соеди-
ним точку
O
1
c точкой A и перпендикулярно радиусу O
1
A в сторону
вращения показываем вектор переносной скорости
1e
V .
В конечный момент, когда точка находится в
B, относительная
скорость
2r
Vu= направлена также по траектории AB в сторону от-
носительного движения. Чтобы показать переносную скорость, со-
единим точку
O
1
c точкой B и перпендикулярно радиусу O
1
B в сто-
рону вращения показываем вектор переносной скорости
2e
V .
Из расчетной схемы видно, что все внешние силы либо парал-
лельны, либо пересекают ось
Oz.

191
Поэтому
1
()0
n
e
zk
k
MF
=
=
∑
и K
z
= const для любого момента вре-
мени, или
2z 1z
K=K. Здесь
1z
K и
2z
K - соответственно кинетиче-
ские моменты системы в начальный и конечный моменты времени.
В общем виде кинетический момент заданной системы вычис-
ляется по формуле
()
пл
zz z1
KK MmV=+ .
Здесь
пл
zzz
K
ω
=
I
- кинетический момент пластины,
()
z1
MmV - кинетический момент точки.
Вычислим момент инерции пластины относительно оси
Oz.
В таблице 11 находим момент инерции прямоугольной пласти-
ны относительно оси, проходящей через центр масс пластины пер-
пендикулярно ее плоскости
22
2
()
3
C
z
mb
′
+
=I
a
.
Момент инерции пластины относительно оси вращения опреде-
лим, используя теорему Гюйгенса – Штейнера
2
22
22
47
212
C
zz
bb
mm
′
+
⎛⎞
=+ =
⎜⎟
⎝⎠
II
a
.
Вычислим кинетический момент системы в начальный момент
времени, когда точка находится в
A.
()
пл
1z 1z z 1 1
KK MmV=+ .
Кинетический момент пластины определяем по формуле
пл
1z z oz
K
ω
= I ,
где
oz
ω
- проекция вектора угловой скорости
o
ω
пластины на ось
вращения
Oz. Пусть пластина в начальный момент времени вра-
щается так, как показано на схеме. Тогда вектор
o
ω
направлен
вверх и
oz o
ω
ω
=
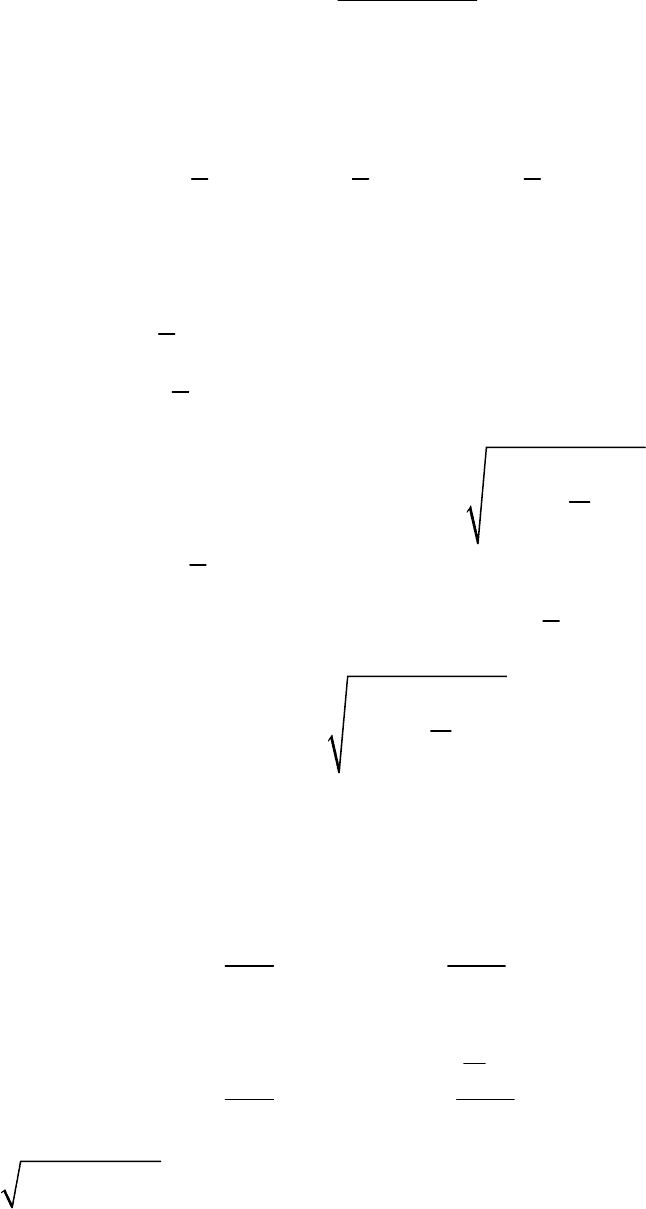
. Следовательно,
192
22
47
12
пл
1z z o 2 o
b
Km
ω
ω
+
==
I
a
.
Кинетический момент точки относительно оси вращения вычис-
лим как сумму кинетических моментов точки в переносном и отно-
сительном движениях
() ( ) ( )
z 11 z 11e z 11r
MmV MmV MmV=+.
Так как
1e o 1
VOA
ω
=
⋅ и
1r
Vu
=
, то, с учетом правила знаков
для моментов, получаем
() (
2
z11e 11e1 o 11
MmV mV OA mOA
)
ω
=⋅=⋅
;
()
z11r 11r 1
MmV mV h muh
=
−⋅=−⋅.
Радиус
OA определяется по формуле
2
2
3
2
1
OA b
⎛⎞
=+
⎜⎟
⎝⎠
a .
Плечо момента
()
z11r
MmV
- h определяется как перпендикуляр,
опущенный из точки O до линии действия вектора
1r
V .
2
2
3
sin( ) sin( )
2
1121 12
hOA OA b
ϕ
ϕϕϕ
⎛⎞
=⋅ −=⋅+ ⋅ −
⎜⎟
⎝⎠
a .
Синус разности двух углов представим в виде
sin( ) sin cos sin cos
12 1 2 2 1
ϕ
ϕϕϕϕϕ
−= ⋅ − ⋅ .
Значения тригонометрических функций находим из рисунка:
2
sin , sin ,
12
1
AB O A
ϕϕ
==
aa
cos , cos ,
12
1
3
b
b
2
AB O A
ϕϕ
==
где
22
(2 )AB b=+a
.
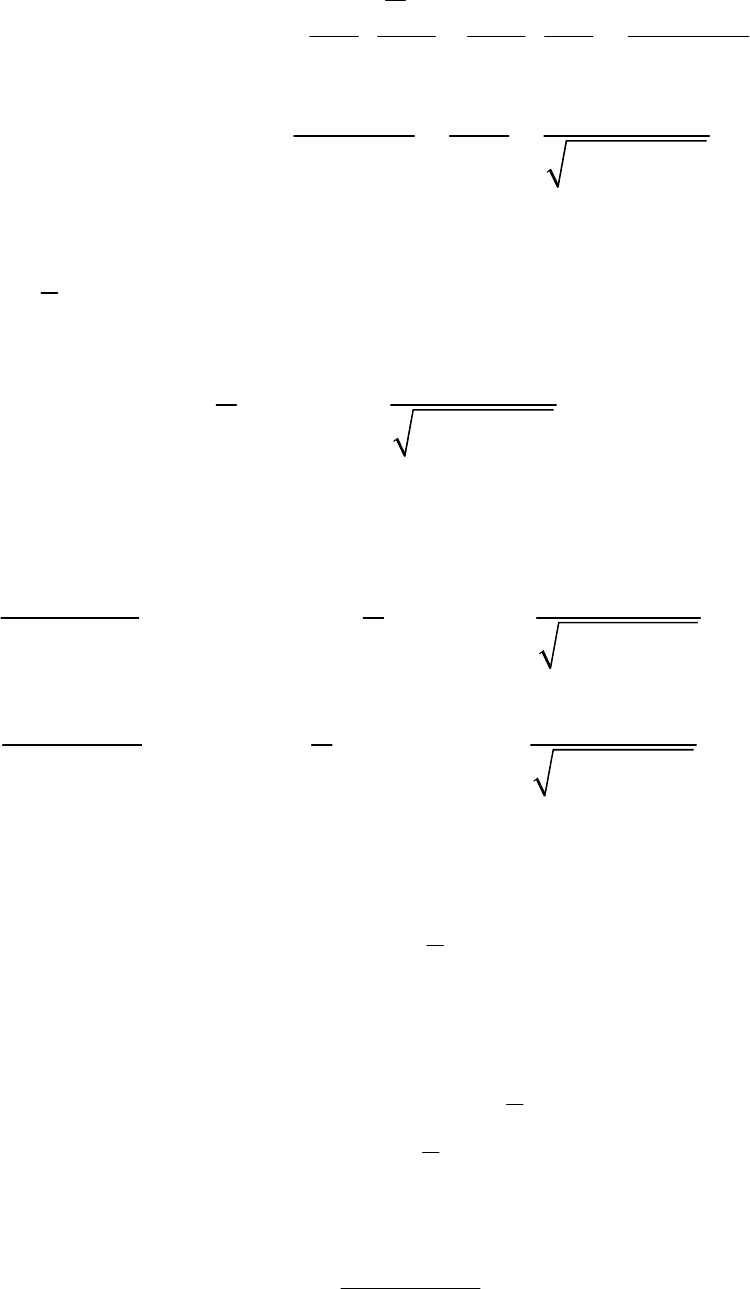
193
Следовательно,
3
22
2
sin( )
12
11 1
b
b
AB OA OA AB OA AB
b
ϕϕ
−=⋅ − ⋅ =
⋅
aa a
и
22
22 2
sin( )
(2 )
1121
1
hOA OA
OA AB AB
b
bb b
ϕϕ
=⋅ −=⋅ = =
⋅
+
aa a
a
.
С учетом найденных значений кинетический момент точки опреде-
лим по формуле
() (
2
z11 o 11 1
MmV mOA
)
mu h
ω
=
⋅−⋅=
2
2
22
32
2
(2 )
1o
mb u
b
b
ω
⎧⎫
⎡⎤
⎪⎪
⎛⎞
=+⋅−
⎢⎥
⎨⎬
⎜⎟
⎝⎠
⎢⎥
+
⎪⎪
⎣⎦
⎩⎭
a
a
a
.
Таким образом, кинетический момент механической системы в на-
чальный момент времени будет равен
2
22
2
22
47 3 2
12 2
(2 )
1z 2 o 1 o
b
Km m b u
b
b
ωω
⎧
⎫
⎡⎤
+
⎪
⎪
⎛⎞
=++⋅−=
⎢⎥
⎨
⎬
⎜⎟
⎝⎠
⎢⎥
+
⎪
⎪
⎣⎦
⎩⎭
aa
a
a
2
22
2
22
47 3 2
12 2
(2 )
21 o1
b
mmbmu
b
b
ω
⎧⎫
⎡⎤
+
⎪⎪
⎛⎞
=++−
⎢⎥
⎨⎬
⎜⎟
⎝⎠
⎢⎥
+
⎪⎪
⎣⎦
⎩⎭
aa
a
a
.
Вычислим кинетический момент механической системы относи-
тельно оси вращения в конечный момент времени, когда точка дос-
тигнет
B
()
пл
2z 2z z 1 2
KKMmV=+ .
Кинетический момент пластины определяем по формуле
пл
2z z z
K
ω
=
I
,
где
z
ω
- проекция вектора угловой скорости
ω
пластины на ось
вращения
Oz. Предположим, что вектор
ω
направлен вверх. Тогда
z
ω
ω
= . Тогда
22
47
12
пл
2z z 2
b
Km
ω
ω
+
==
I
a
.
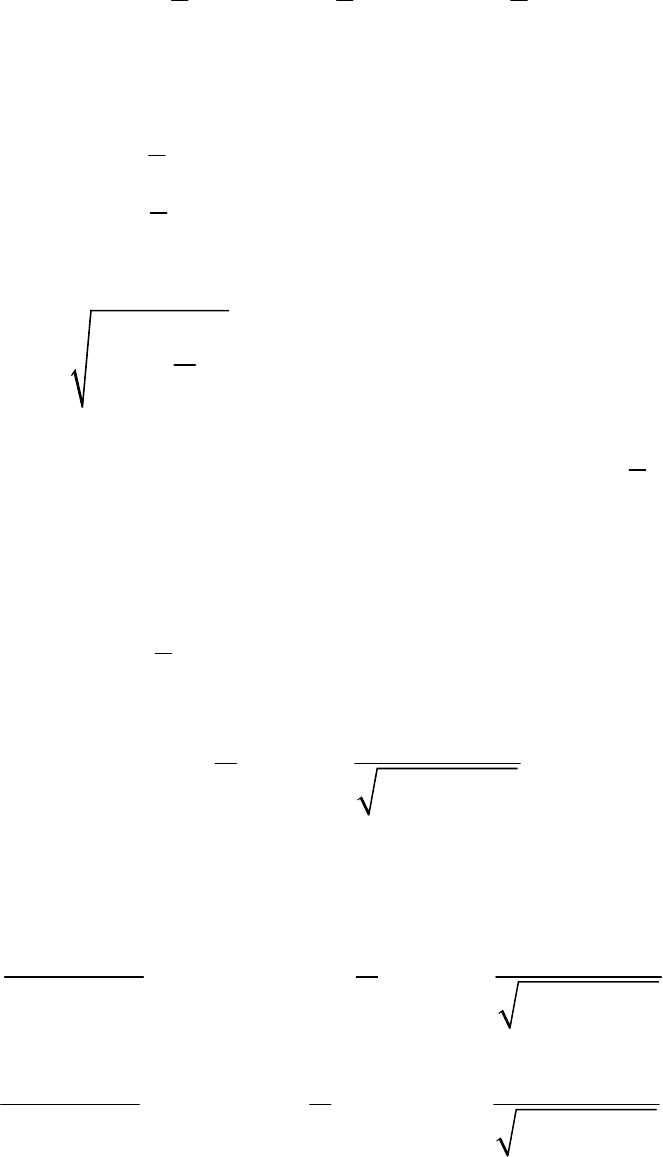
194
Кинетический момент точки относительно оси вращения вычис-
лим как сумму кинетических моментов точки в переносном и отно-
сительном движениях
()( )( )
z 12 z 12e z 12r
MmV MmV MmV=+.
Так как
2e 1
VOB
ω
=⋅ и
2r
Vu
=
, то, с учетом правила знаков для
моментов, получаем
() (
2
z12e 12e 1 11
MmV mV OB mOB
)
ω
=⋅=⋅
;
()
z12r 12r 1
MmV mV h muh
=
−⋅=−⋅
.
Радиус вращения в переносном движении
OB определяется по
формуле
2
2
2
1
b
OB
⎛⎞
=+
⎜⎟
⎝⎠
a .
Так как траектория относительного движения – прямая линия
AB,
то расстояние h от точки
O
1
до линии действия вектора
2r
V такое
же, как и в первом случае.
С учетом найденных значений кинетический момент точки опреде-
лим по формуле
() (
2
z12 11 1
MmV mOB) muh
ω
=
⋅−⋅=
2
2
22
2
2
(2 )
1
b
mu
b
b
ω
⎧⎫
⎡⎤
⎪⎪
⎛⎞
=+⋅−
⎢⎥
⎨⎬
⎜⎟
⎝⎠
⎢⎥
+
⎪⎪
⎣⎦
⎩⎭
a
a
a
.
Таким образом, кинетический момент механической системы в ко-
нечный момент времени будет равен
2
22
2
22
47 2
12 2
(2 )
2z 2 1
bb
Km m u
b
b
ωω
⎧
⎫
⎡⎤
+
⎪
⎪
⎛⎞
=++⋅−=
⎢⎥
⎨
⎬
⎜⎟
⎝⎠
⎢⎥
+
⎪
⎪
⎣⎦
⎩⎭
aa
a
a
2
22
2
22
47 2
12 2
(2 )
21 1
bb
mm mu
b
b
ω
⎧⎫
⎡⎤
+
⎪⎪
⎛⎞
=++−
⎢⎥
⎨⎬
⎜⎟
⎝⎠
⎢⎥
+
⎪⎪
⎣⎦
⎩⎭
aa
a
a
.
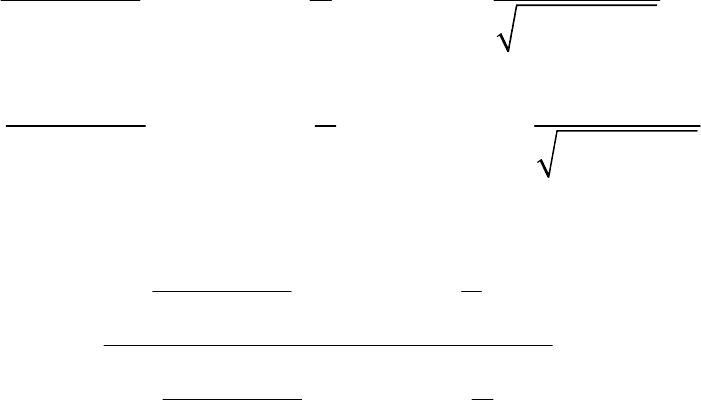
Приравняем значения
2z
K и
1z
K
195
2
22
2
22
47 2
12 2
(2 )
21 1
bb
mm mu
b
b
ω
⎧⎫
⎡⎤
+
⎪⎪
⎛⎞
++ − =
⎢⎥
⎨⎬
⎜⎟
⎝⎠
⎢⎥
+
⎪⎪
⎣⎦
⎩⎭
aa
a
a
2
22
2
22
47 3 2
12 2
(2 )
21 o1
b
mmbmu
b
b
ω
⎧⎫
⎡⎤
+
⎪⎪
⎛⎞
=++−
⎢⎥
⎨⎬
⎜⎟
⎝⎠
⎢⎥
+
⎪⎪
⎣⎦
⎩⎭
aa
a
a
.
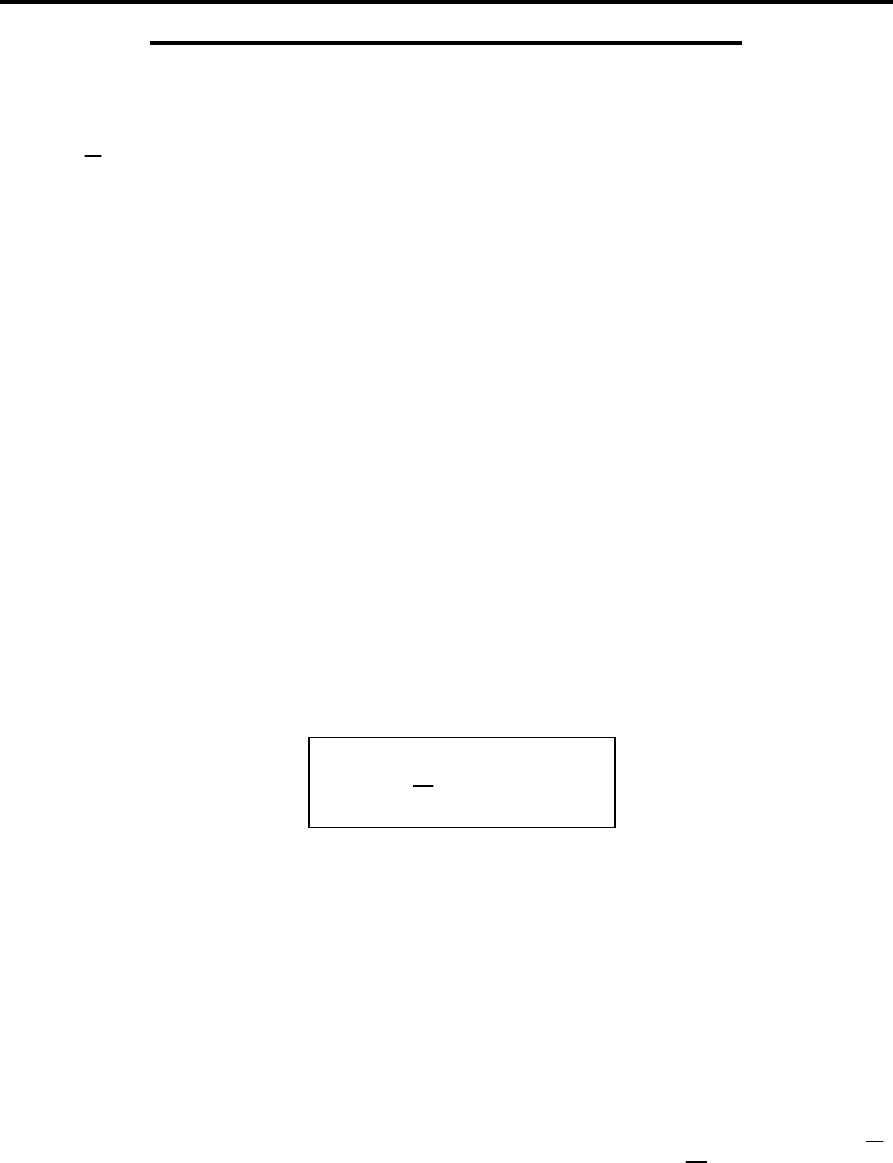
Отсюда получаем ответ
2
22
2
2
22
2
47 3
12 2
47
12 2
21
o
21
b
mmb
bb
mm
ω
ω
⎡
⎤
+
⎛⎞
++
⎢
⎥
⎜⎟
⎝⎠
⎢
⎥
⎣
⎦
=
⎡⎤
+
⎛⎞
++
⎢⎥
⎜⎟
⎝⎠
⎢⎥
⎣⎦
a
a
a
a
.
196
Задача Д.3. Теорема об изменении кинетической
энергии механической системы
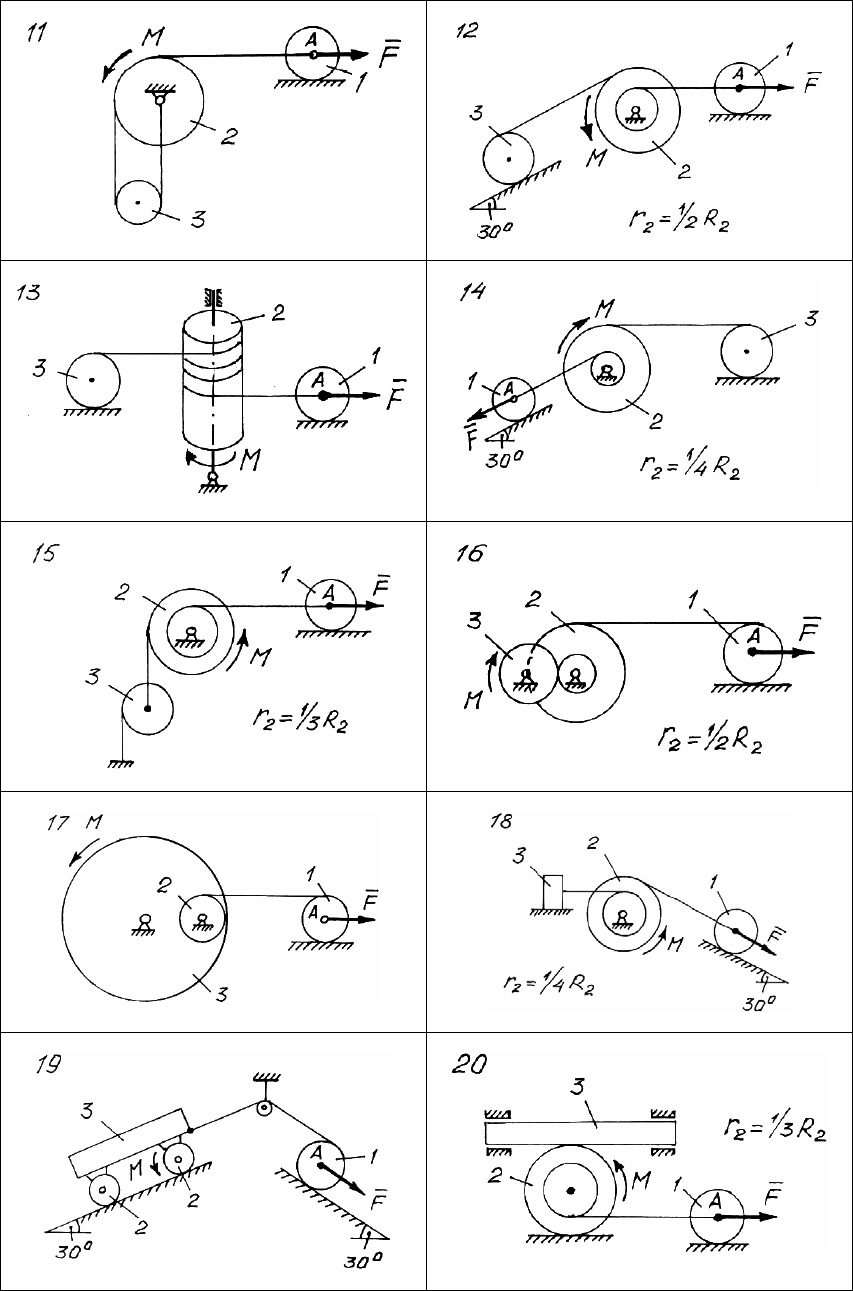
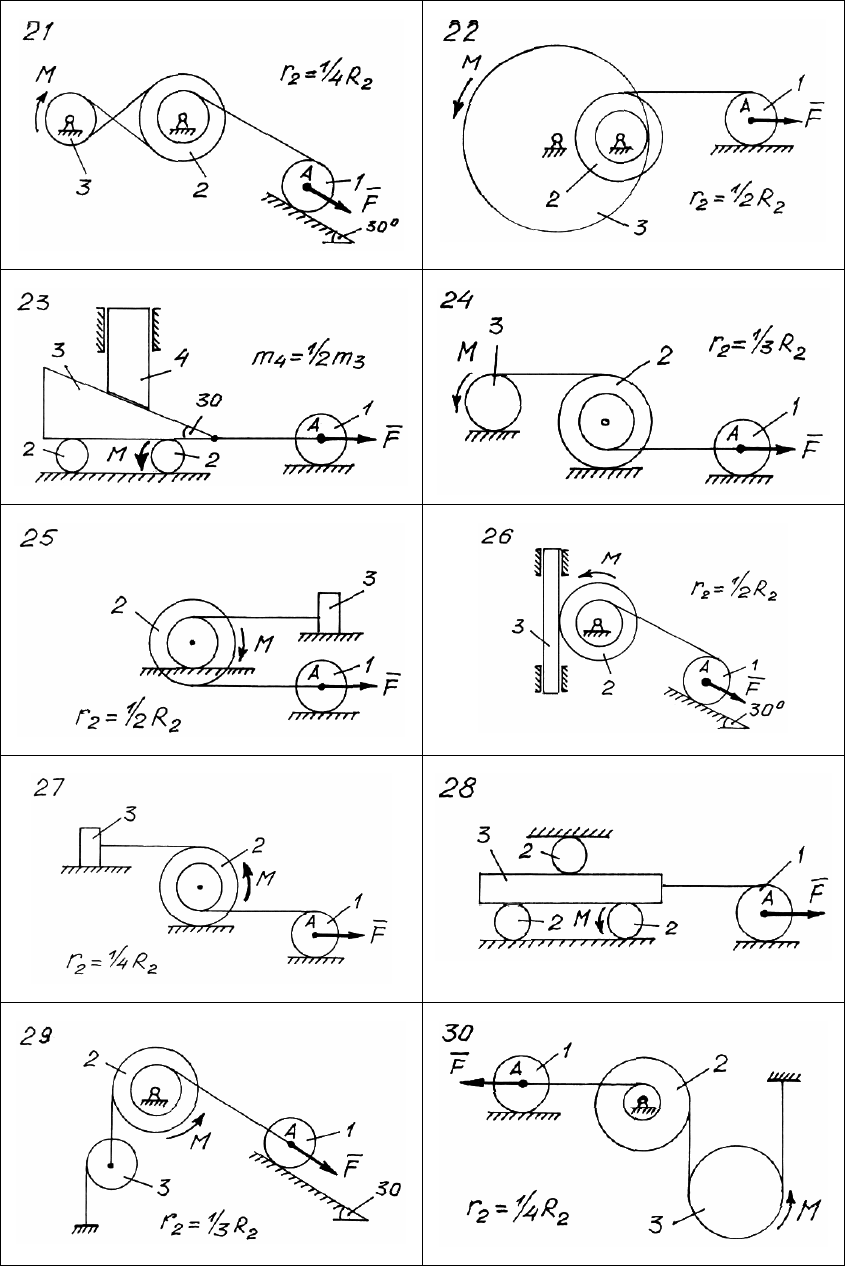
Механическая система (рис. 123 – 125) движется под действием
силы
F , приложенной к катку 1. В системе действует момент со-
противления M. В вариантах 18, 20, 23, 25, 26, 27 тела 3 и 4 сколь-
зят по гладкой поверхности.
При заданных величинах (таблица 12) во всех вариантах схем
определить ускорение точки A тела 1.
Для всех вариантов радиус катка 1 R
1
= 1м.
Теорема об изменении кинетической энергии
механической системы
Кинетическая энергия – это качественная характеристика меха-
нического движения точки и механической системы, твердого тела.
Кинетическая энергия механической системы будет определять-
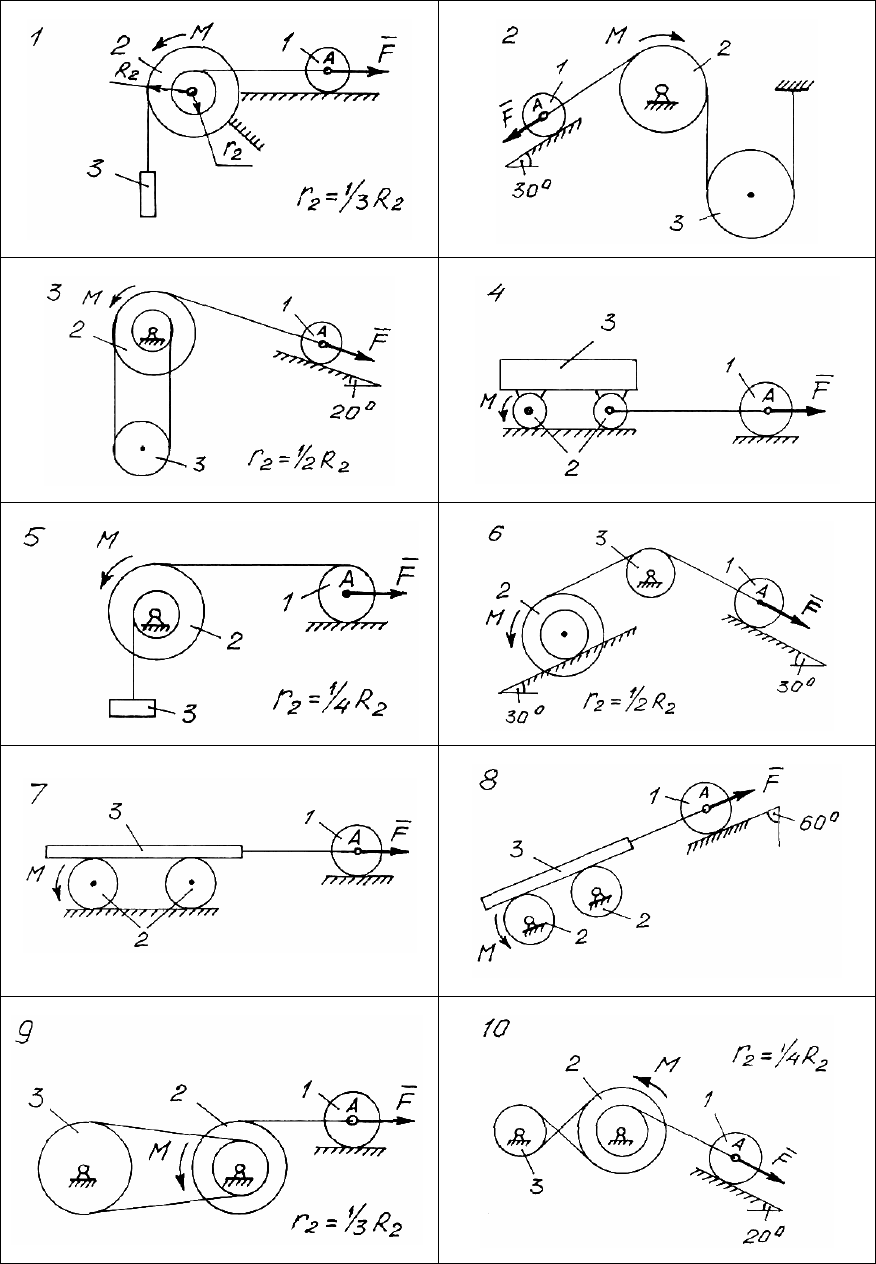
ся по формуле:
; , ,
где
k
mm=
∑
- масса механической системы;
C
V - скорость центра масс при поступательном движении
системы;
r
C
T
- сумма кинетических энергий каждой материальной точ-
ки в относительном движении, по отношению к центру масс C.
В общем случае для механической системы
2
1
1
2
n
kk
k
TmV
=
=
∑
, где
k
V
- абсолютная скорость k – ой точки;
2
1
2
r
CC
TmVT
=
+
197
Рис. 123
198
Рис. 124
199
Рис. 125
