Теоретическая механика - теория, задания и примеры решения задач
Подождите немного. Документ загружается.

250
Рис. 164
251
Рис. 165
252
где
1
n
k
k
FF
=
=
∑
- равнодействующая заданных сил;
N - реакция связи;
m - масса точки.
Величину
m a перенесем в правую часть равенства (8) и полу-
чим
0=F+N-ma.
Величину
m Ф−=a
- называют силой инерции точки. Тогда
. (2)
В каждый момент времени активная сила
F , сила реакции свя-
зи
N и сила инерции Ф образуют систему уравновешенных сил,
действующих на точку M. Равенство (2) выражает принцип Далам-
бера для материальной точки или, как его иногда называют, метод
кинетостатики.
Так как система сил
{
;;
}
FNФ эквивалентна нулю, то к ней
можно применять уравнения статики. При этом сила инерции
Ф по
модулю равна
Ф = ma и всегда направлена в обратную сторону от
ускорения точки.
1.2 Механическая система
На k – тую точку механической системы (рис. 166) действуют
внешняя
e
k
F и внутренняя
i
k
F силы.
Покажем силу инерции
k
Ф , направив ее в обратную сторону от
k
a . Согласно принципу Даламбера для каждой точки M
k
запишем
соотношение
0
ei
kkk
FFФ++ =; где
1,kn=
. (3)
0FNФ
+
+=
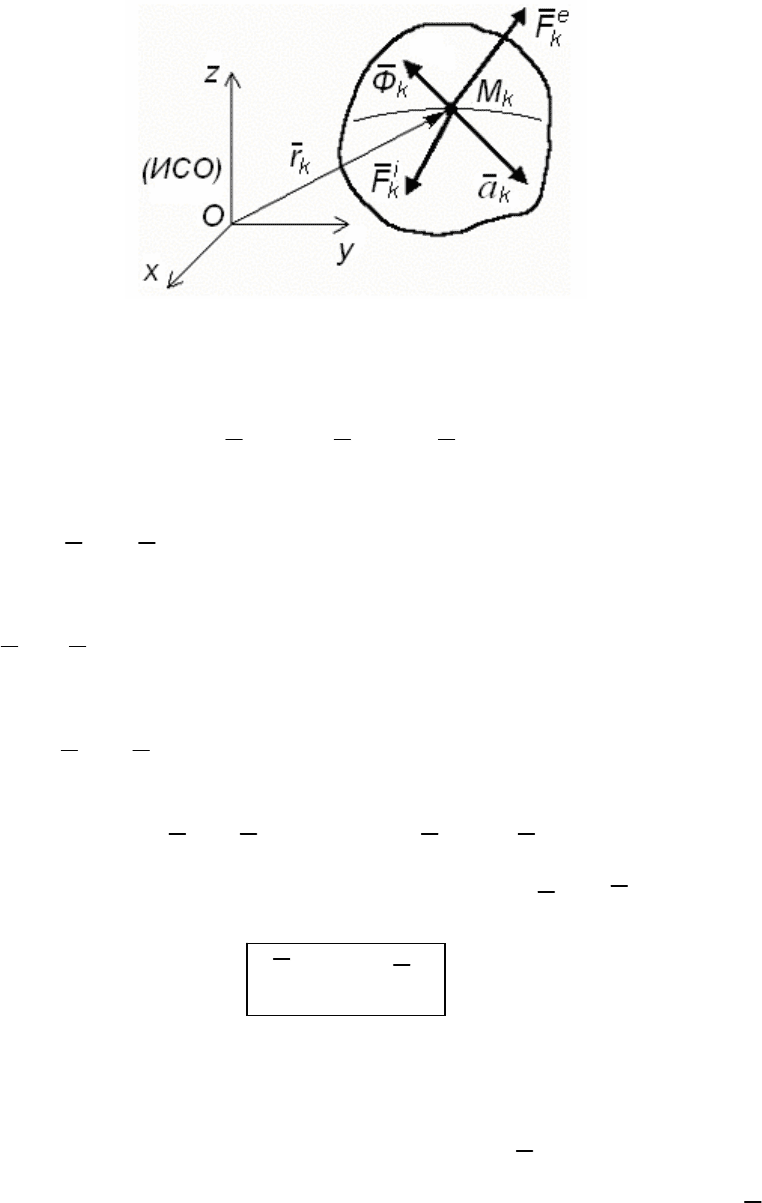
253
Рис. 166
Получим систему n – уравнений. Просуммируем эти уравнения
111
0
nnn
ei
kkk
kkk
FFФ
===
+
+=
∑∑∑
.
Здесь
1
n
ee
k
k
FR
=
=
∑
- главный вектор внешних сил;
1
0
n
ii
k
k
FR
=
==
∑
- главный вектор внутренних сил;
1
n
Ф
k
k
Ф R
=
=
∑
- главный вектор сил инерций.
Следовательно,
0
e Ф
RR+=, и
Ф e
RR
=
− . Из теоремы о
движении центра масс механической системы
e
C
mR=a
находим
. (4)
Главный вектор сил инерции, по модулю, определяется произ-
ведением массы системы на ускорение центра масс (
R
Ф
= ma
C
) и
направлен в обратную сторону от направления
с
a
.
Теперь равенство (3) векторно умножим на радиус-вектор
k
r ,
который соединяет неподвижную точку O (инерциальная система
отсчета) с материальной точкой M
k
Ф
C
Rm=− a
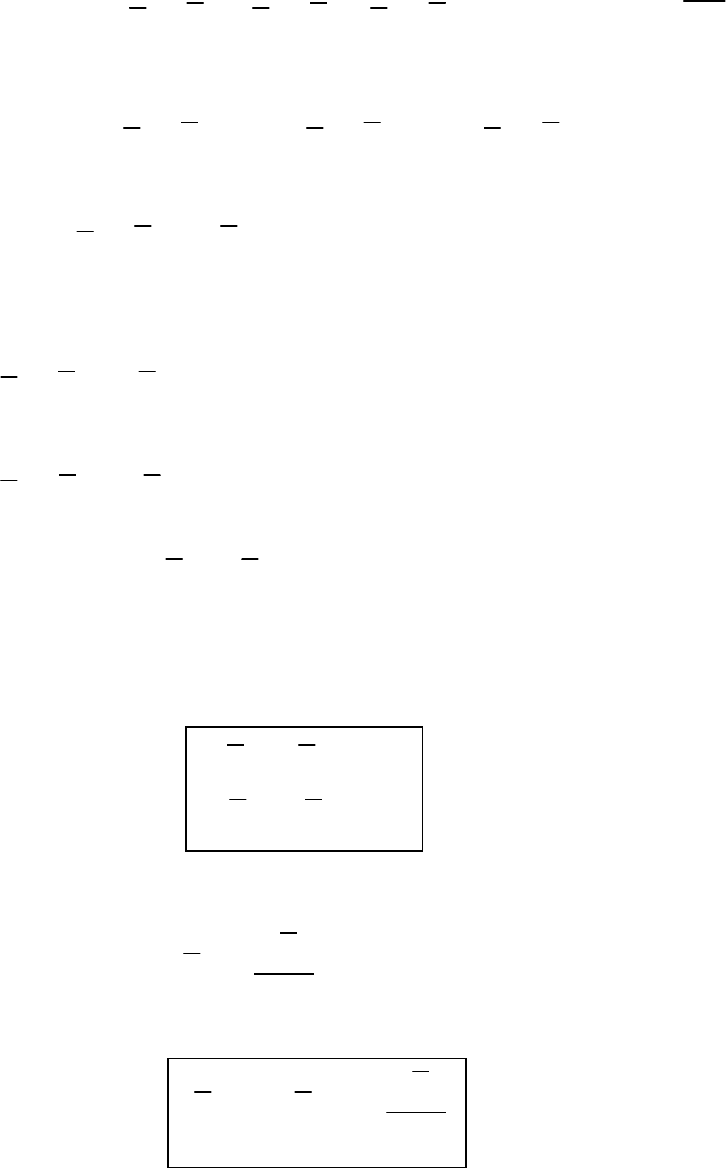
254
0
ei
kk kkk k
rF rFrФ×+×+×=,
k=1,n
.
Просуммируем все уравнения
111
()()()
0
nnn
ei
kk kk k k
kkk
rF rF rФ
=
==
×+ ×+ ×=
∑∑∑
.
Здесь
1
()
n
ee
kk o
k
rF M
=
×=
∑
- главный момент внешних сил отно-
сительно центра приведения точки O;
1
()
0
n
ii
kk o
k
rF M
=
×==
∑
- главный момент внутренних сил;
1
()
n
Ф
kk o
k
r Ф M
=
×=
∑
- главный момент сил инерций.
Следовательно,
0
e Ф
oo
MM+=
.
Для механической системы принцип Даламбера запишется в
следующем виде:
(5)
.
Из теоремы об изменении кинетического момента механиче-
ской системы следует
e
o
o
dK
M
dt
=
, поэтому
. (6)
0;
0.
e Ф
e Ф
oo
RR
MM
⎧
+
=
⎪
⎨
+
=
⎪
⎩
Ф e
o
oo
dK
MM
dt
=− =−
255
1.3 Приведение сил инерций твердого тела
к простейшему виду
а) Поступательное движение твердого тела
При поступательном движении тела (σ) все силы инерции при-
водятся в центр масс (точка C) к главному вектору
Ф
R (рис. 167),
который по модулю равен и направлен в обратную
сторону от
с
a (m – масса тела).
Рис. 167
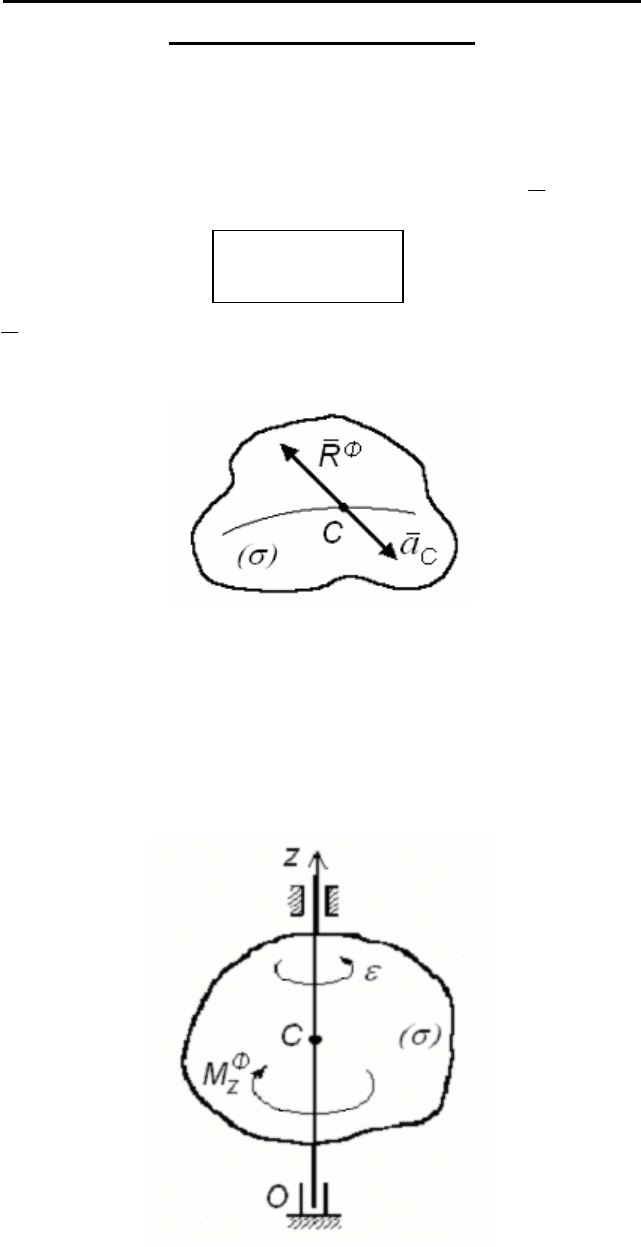
б) Вращение тела вокруг неподвижной оси
Пусть ось вращения Oz (рис. 168) тела (σ) проходит через
центр масс тела (точка C) этого тела.
Рис. 168
C
Ф
R =ma
256
На основании (6)
Ф
z
z
dK
M
dt
=
, но
zz
K
ω
=
I
, тогда при I
z
= const,
получим , где I
z
– момент инерции тела (σ) относи-
тельно оси Oz.
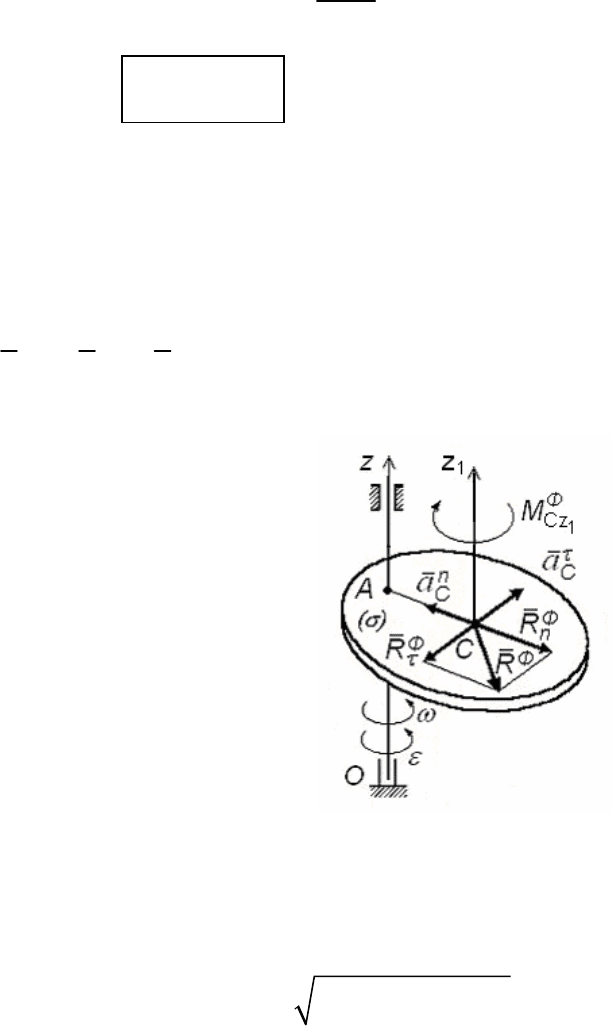
Теперь рассмотрим случай (рис. 169), когда ось вращения Oz
тела (σ) не проходит через центр масс (точку C).
Силы инерции тела (σ) приводятся в точку C к главному вектору
ФФФ
n
RRR
τ
=+
и главному моменту
1
Ф
Сz
M .
Рис. 169
При этом
Ф
C
Rm mAC
τ
τ
ε
==⋅⋅a ;
2Ф n
nC
Rm m AC
ω
==⋅⋅a ;
11
Ф
Сz Сz
M
ε
=⋅I ;
22
()()
ФФФ
n
RRR
τ
=+.
в) Плоское движение твердого тела
Фигура (σ) перемещается поступательно с центром масс (точка
C) и вращается относительно центра масс (рис. 170).
Ф
zz
M
ε
= I
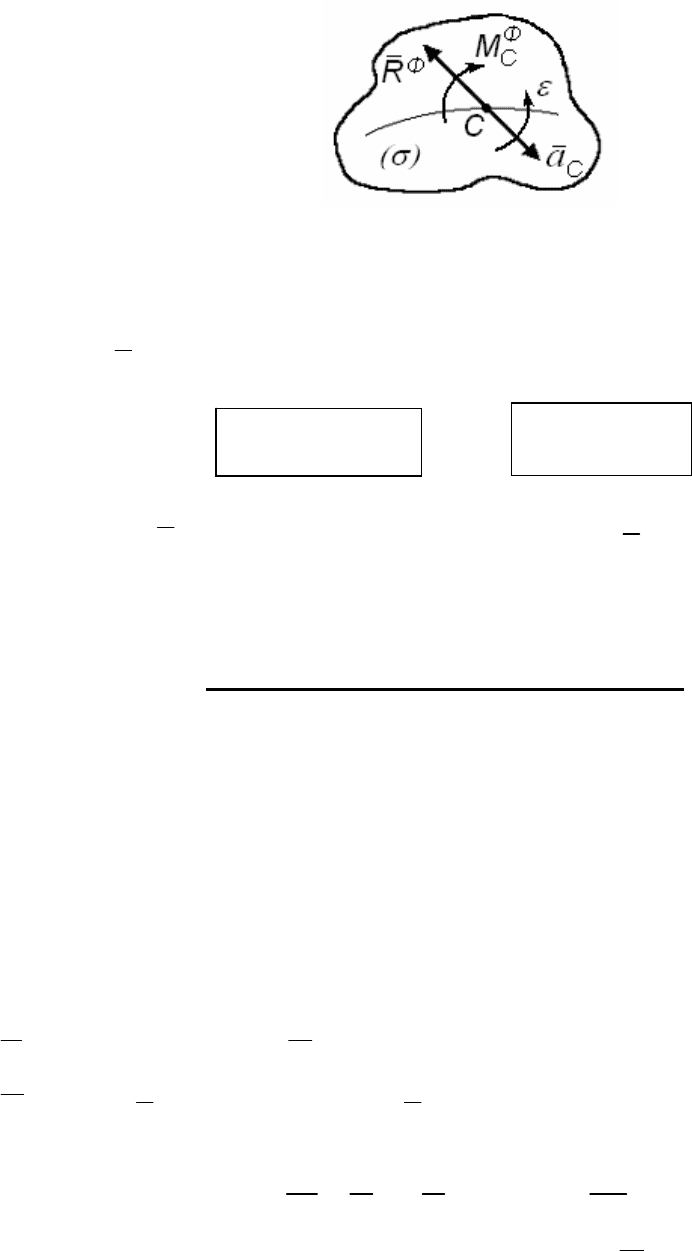
257
Рис. 170
Силы инерции приводятся в центр масс (точка C) к главному
вектору
Ф
R и главному моменту
Ф
M . При этом
и .
Вектор
Ф
R направлен в сторону обратную
с
a ,
Ф
M - в обратную
сторону от
ε
.
2.Общее уравнение динамики
Если система находится в движении и имеет стационарные
(склерономные), двусторонние (удерживающие) и идеальные свя-
зи, то сумма работ активных (заданных) сил и сил инерций на соб-
ственных возможных перемещениях равна нулю.
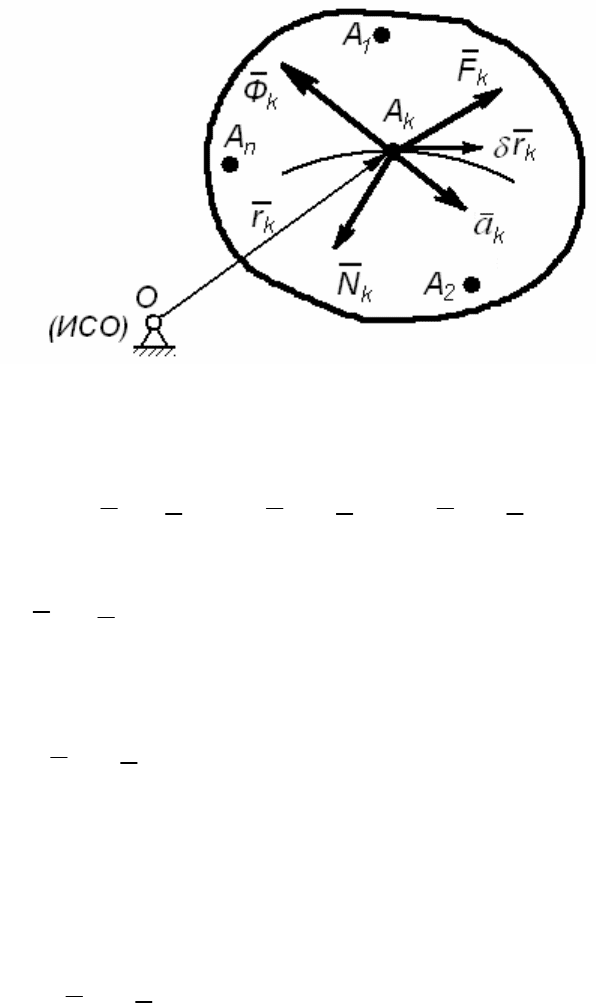
На рис. 171 показана механическая система, которая переме-
щается относительно инерциальной системы отсчета (т.О).
Рассмотрим
k
A точку, на которую действуют следующие силы:
k
F - активная сила;
k
N - реакция связи, наложенной на точку;
k
kk
Ф m=− a - сила инерции (
k
a - ускорение точки,
k
m - масса точ-
ки). Cогласно принципу Даламбера для точки, можно записать:
0
kk
k
FN Ф++= (
1,kn=
) . (7)
Теперь равенство умножим скалярно на
k
rδ - возможное пере-
мещение точки. Получим n - уравнений, а затем просуммируем все
Ф
C
Rm=⋅a
Ф
C
M
ε
=
⋅I
258
Рис. 171
уравнения, получим
11 1
0
nn n
kk kk kk
kk k
Fr Nr Ф r
δδδ
=
==
⋅+ ⋅+ ⋅=
∑∑∑
.
Тогда
11
nn
kk k
kk
Fr A
δ
δ
==
⋅=
∑∑
a
- сумма работ активных сил на соб-
ственных возможных перемещениях;
11
nn
N
kk k
kk
Nr A
δδ
==
⋅=
∑∑
- сумма работ реакций связей на
возможных перемещениях. Но при идеальных связях (по опреде-
лению)
.0A
n
1k
N
k
=
∑
=
δ
1
n
Ф
kk k
k
Ф rA
δ
δ
=
⋅=
∑
- сумма работ сил инерций на воз-
можных перемещениях.
Теперь окончательно можно записать:
11
0
nn
АФ
kk
kk
AA
δδ
=
=
+
=
∑∑
. (8)
259
Уравнение работ (8) будет называться общим уравнением ме-
ханики.
Пример решения задачи
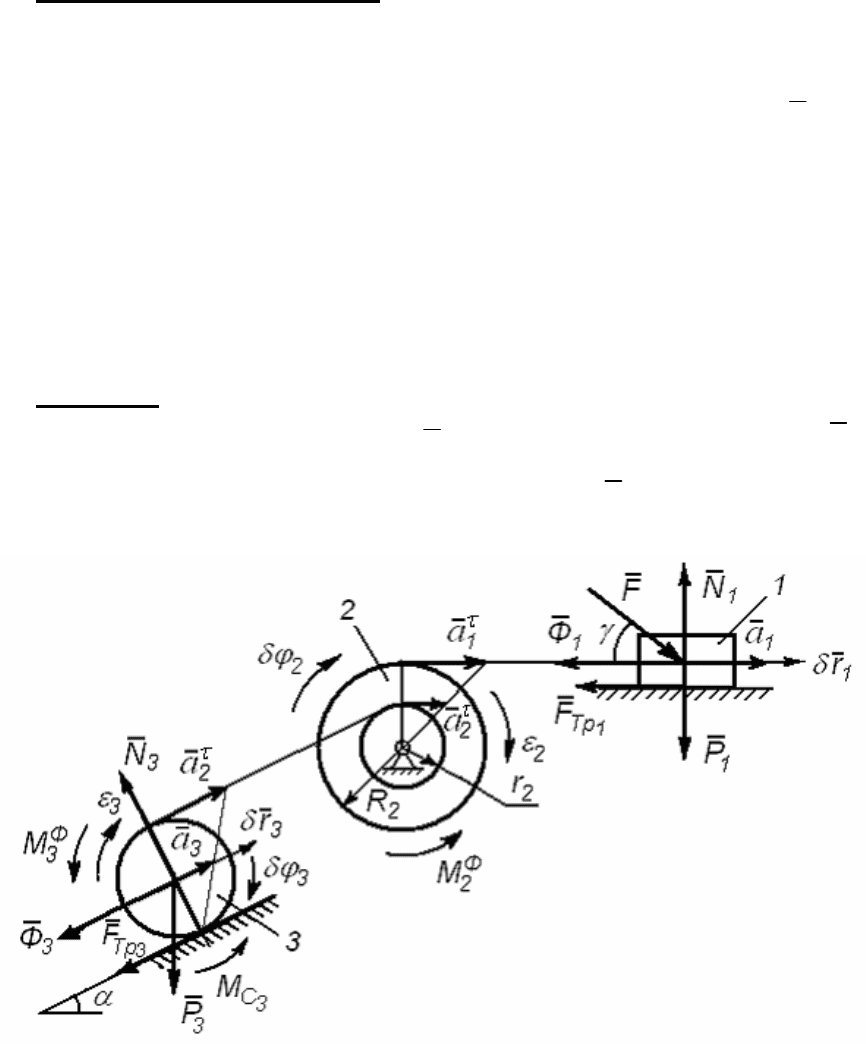
На рис. 172 показана механическая система, состоящая из
трех тел, соединенных между собой нерастяжимыми нитями.
Дано:
321
m,m,m
- массы тел;
223
,,rRr
- радиусы тел; F - ак-
тивная сила;
a
,
g
- углы;
r
2
- радиус инерции тела 2;
f
- коэффици-
ент трения скольжения тела 1;
k - коэффициент трения качения те-
ла 3.
Определить ускорение тела 1 (
1
a ).
Решение
Покажем ускорение тела 1
1
a в сторону действия силы
F
и
найдем ускорения тел 2 и 3, выразив их через
1
a .
Рис. 172
