Теоретическая механика - теория, задания и примеры решения задач
Подождите немного. Документ загружается.

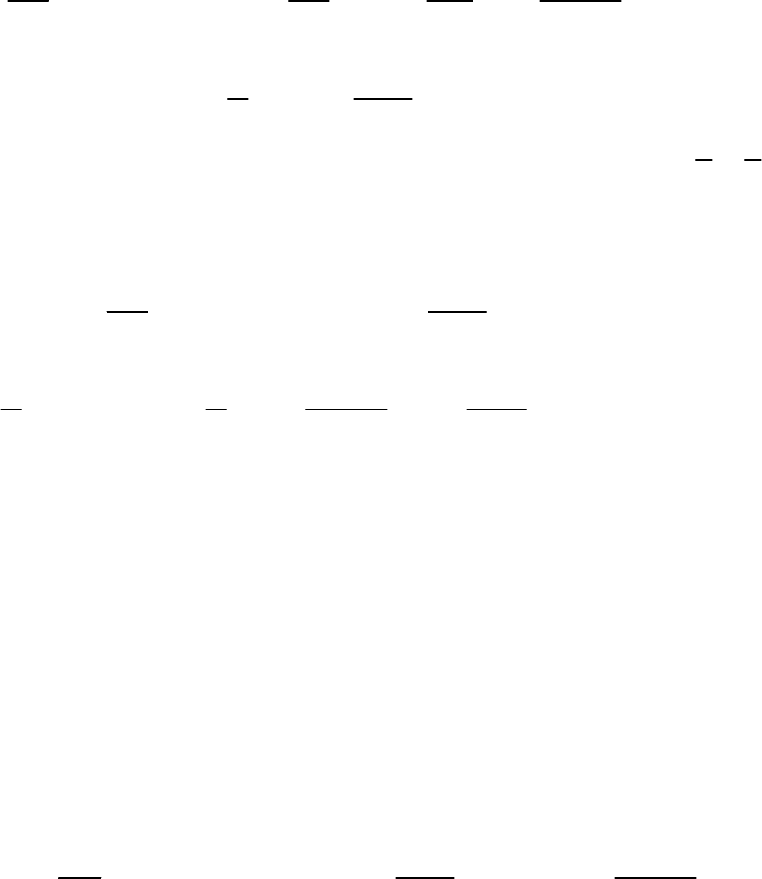
260
Кинематические соотношения:
1
2
2
;
R
τ
ε
=
a
2
2221
2
;
r
r
R
τ
ε
=⋅=aa
22
31
232
;
22
r
rrR
τ
ε
==
a
a
2
321 11
2
1
;.
22
r
R
τ
τ
== =aaa aa
Покажем активные силы
gmP
11
=
, gmP
33
=
; реакции
13
,NN.
Факторы инерции :
111
Ф m
=
a ;
222
Ф
MI
ε
= ;
2
222
Im
ρ
= ;
2
1
222
2
Ф
Mm
R
ρ
=
a
;
2
33331
2
2
r
Ф mm
R
==aa
;
333
Ф
MI
ε
=
;
2
333
1
2
Imr= ;
2
23
12
333 31
32 2
1
22 4
Ф
rr
r
Mmr m
rR R
==
a
a
.
Далее показываем возможные перемещения тел и, применяя
общее уравнение динамики (8), составляем сумму работ всех сил
на собственных возможных перемещениях точек приложения
1 11 1 2 2 33 33
cos sin
Ф
тр
Fr Ф rF rM Pr Ф r
δγδ δ δϕδαδ
⋅−−−− −−
3
33 3
0
Ф
c
MM
δϕ δϕ
−− =
.
При стационарных (склерономных) связях возможные переме-
щения совпадают с действительными.
Тогда
1
2
2
;
r
R
δ
δϕ
=
333
;rr
δ
δϕ
=
2
31
2
;
2
r
rr
R
δ
δ
=
2
31
32
.
2
r
r
rR
δ
ϕδ
=
Определим силу трения скольжения.
fNF
11.тр
= ; γγ sinFgmsinFPN
111
+
=
+
=
;
.1 1
sin
тр
FmgfFf
γ
=
+ .
Момент сопротивления качению
3
3С
MkN= ;
33 3
cos cosNP mg
α
α
== ;
3
3
cos
C
Mkmg
α
=
.
Полученные величины подставим в уравнение

261
2
11
111111 122
22
cos sin
r
Fr m r mgfr Ff r m
RR
δ
δγ δ δ γδ ρ
−− − − ⋅−
a
a
23
222 2
31311311
222 232
1
sin
22242
rr
rrr r
mg r m r m r
RRR RrR
αδ δ δ
−⋅−⋅ − −aa
2
31
32
cos 0
2
r
mgk r
rR
αδ
−=
.
При
1
0r
δ
≠ , эта величина уходит. Члены, содержащие
1
a , пе-
реносим в другую часть равенства.
22
13 3
232
(cos sin ) sin cos
22
rrk
Ffmfmg mg
RrR
γ
γαα
−−− − =
22
22
11 2 3
22
22
3
.
8
rr
mm m
RR
⎛⎞
=++
⎜⎟
⎝⎠
a
Окончательно получим
2
13
23
1
22
22
12 3
22
22
(cos sin ) (sin cos )
2
3
8
rk
Ffmgfmg
Rr
rr
mm m
RR
γ
γαα
−−− +
=
++
a .
Чтобы направление вектора
1
a не изменилось, на числитель
полученной формулы нужно наложить условие
2
13
23
(
cos sin
)
>
(
sin cos
)
.
2
rk
Ffmgfmg
Rr
γ
γαα
−+ +
Если
2
13
23
(
cos sin
)(
sin cos
)
2
rk
Ffmgfmg
Rr
λ
γαα
−=+ + , то
система будет находиться в покое, или тело 1 будет иметь посто-
янную скорость движения
1
()constv
=
.

262
Задача Д.7. Дифференциальные уравнения
движения механической системы
в обобщенных координатах
(уравнение Лагранжа второго рода)
Для механической системы (рис. 163 - 165), имеющей одну сте-
пень свободы, определить ускорение тела 1, применив уравнение
Лагранжа
1
второго рода.
1. Обобщенные координаты
Обобщенными координатами называются независимые ве-
личины, линейные или угловые, заданием которых однозначно оп-
ределяется положение материальных точек механической системы
в пространстве или на плоскости. Обобщенные координаты зависят
от параметра времени: q = q(t) – линейная обобщенная координата;
ϕ
=
ϕ
(t) – угловая обобщенная координата. Первые производные по
времени от обобщенных координат называются обобщенными ско-
ростями:
()qqt=
;
()
t
ϕ
ϕ
=
. Число степеней свободы s механи-
ческой системы определяет количество обобщенных координат.
На рис. 173
a показана схема математического маятника, кото-
рый колеблется в вертикальной плоскости. Положение точки M
можно зафиксировать только углом
ϕ
=
ϕ
(t) – обобщенной угловой
координатой. Схема эллиптического маятника показана на рис.
173б. Эта система имеет две степени свободы, поэтому и вводятся
две обобщенные координаты:
ϕ
=
ϕ
(t) – угол отклонения от верти-
кали нити вместе с точкой M; q = q(t) – поступательное перемеще-
ние тела 1 вдоль горизонтальной плоскости.
1
Лагранж Жозеф Луи (25.1.1736 – 10.4.1813). Французский математик и меха-
ник, член Французской АН с 1772 г. В работе “Аналитическая механика” (1788)
Лагранж подвел итог всему, что было создано в механике на протяжении 18 века.

263
Рис. 173
2. Вычисление кинетической энергии механической
системы через обобщенные координаты
При наличии обобщенных координат в механической системе,
радиус – вектор любой k – той точки будет функцией этих коорди-
нат и параметра времени t:
1, 2
(
,,,
)
kk s
rrqq qt= … .
Тогда дифференциал функции
k
r запишется в виде:
1
1
kkkk
kis
is
rrrr
dr dq dq dq dt
qqqt
∂∂∂∂
=++++ +
∂∂∂∂
……
.
Если это равенство разделить на dt, то
k
k
dr
dt
v
=
- вектор скорости
k – той точки.
Тогда
1
s
kk
ki
i
i
rr
q
qt
v
=
∂
∂
=+
∂
∂
∑
. (1)
Из формулы (1) можно получить равенство
kk
ii
r
qq
v
∂
∂
=
∂
∂
, (2)
которое понадобится при выводе уравнений Лагранжа 2-го рода.
Кинетическая энергия механической системы
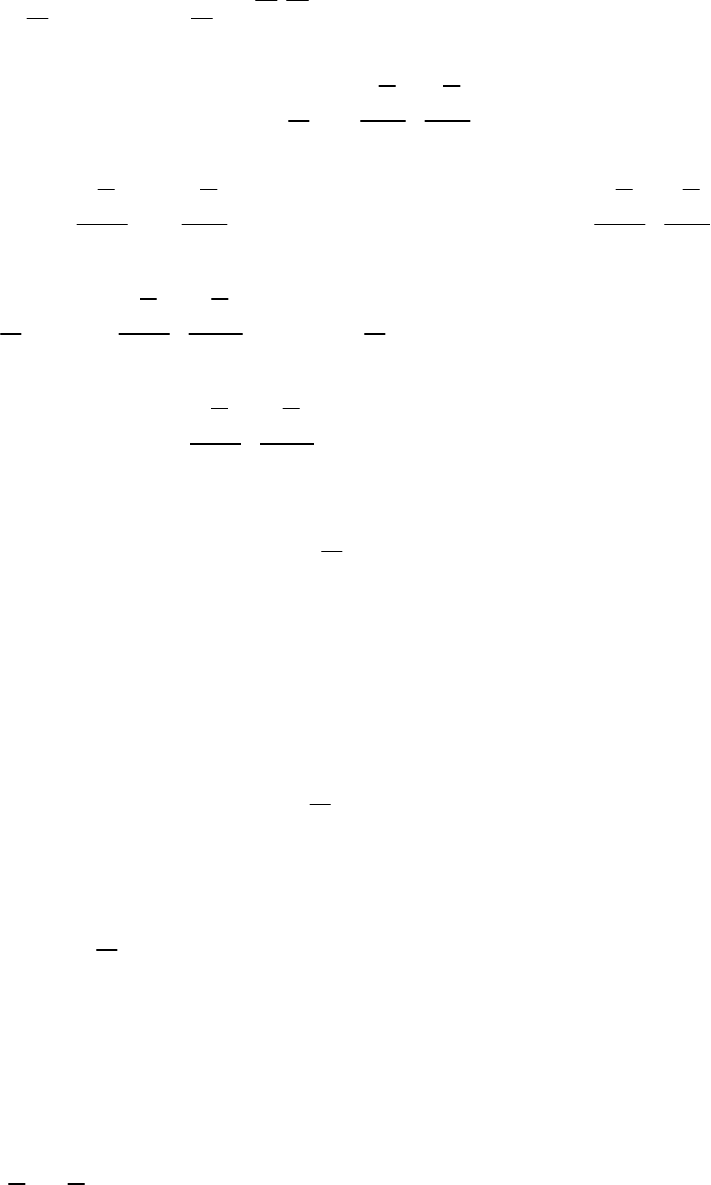
264
nn
2
kk kkk 0 1 2
k=1 k=1
11
T= m = m =T +T +T
22
vvv
∑∑
,
где с учетом (1),
0
1
1
2
n
kk
ko
k
rr
Tm
tt
=
∂∂
=⋅=
∂∂
∑
a ;
1
11 1
nN N
kk
kj ji
j
kj j
rr
Tm q q
qt
== =
∂∂
=⋅=
∂∂
∑∑ ∑
a , где
1
n
kk
jk
j
k
rr
m
qt
=
∂∂
=
⋅
∂∂
∑
a ;
2
1(,) (,)
11
22
n
kk
kjpjpjp
jp
kjp jp
rr
Tm qq qq
qq
=
∂∂
=⋅⋅=⋅
∂∂
∑∑ ∑
a
,
где
1
n
kk
jp pj k
j
p
k
rr
m
qq
=
∂∂
== ⋅
∂∂
∑
aa .
Тогда
0
1(,)
1
2
N
j
ijpjp
jjp
Tqqq
=
=
++ ⋅
∑∑
aa a
, (3)
где
a
jp
– коэффициенты инерции (масса или моменты инерции).
Если механическая система имеет стационарные (склероном-
ные) связи, то
a
0
= a
j
= 0, тогда формула (3) запишется в виде:
(, )
1
2
j
pj p
jp
Tqq
=
⋅
∑
a
. (4)
Например, если система имеет две степени свободы (q
1
= q
1
(t), q
2
=
q
2
(t)), то
22
11 1 12 1 2 22 2
1
(2 )
2
Tqqqq=+ +
aa a.
3. Обобщенные силы
Для голономной механической системы, которая имеет стацио-
нарные (склерономные) связи, возможное приращение радиус –
вектора
1, 2
(
,,
)
kk s
rrqq q= … при фиксированном значении времени
(
δ
t = 0) зависит только от
δ
q
i
и его можно записать в следующем
виде:
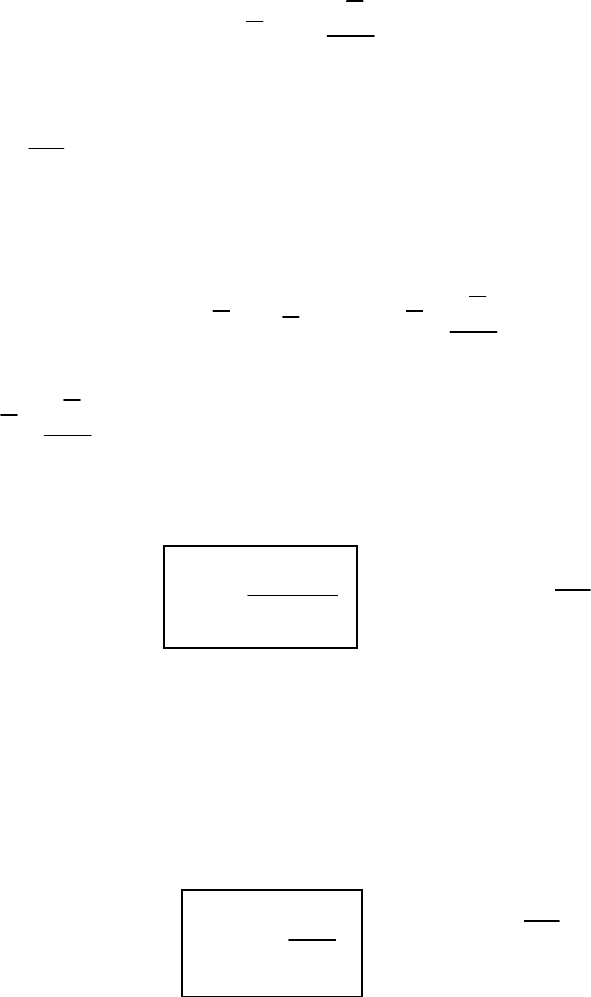
265
()
k
ki i
i
r
rq
q
δ
δ
∂
=
∂
, (5)
где
δ
q
i
– возможное приращение обобщенной координаты
q
i
= q
i
(t); 1,is= .
Запишем выражение для работы заданных сил на возможном
перемещении i –той точки:
11
() ()
nn
k
ki k ki k i
i
kk
r
AFrFq
q
δ
δδ
==
∂
=⋅=⋅
∂
∑∑
,
где
1
n
k
ki
i
k
r
FQ
q
=
∂
⋅=
∂
∑
- обобщенная сила активных сил.
Тогда
()
ki i i
AQq
δ
δ
= , откуда
(
1,is= ). (6)
Формула (6) позволяет выполнять практическое вычисление
обобщенной силы при решении задач. Обобщенная сила Q
i
может
иметь размерность силы (Н), или размерность момента силы (Нм).
Если механическая система консервативная, то обобщенную силу
можно вычислять по формуле
(
1,is=
), (7)
где П = П(q
1
, q
2
,. . . , q
s
) – потенциальная энергия системы.
4. Вывод уравнений Лагранжа второго рода
Рассмотрим голономную механическую систему, которая имеет
стационарные (склерономные), идеальные и двусторонние связи. В
системе будут действовать активные силы и реакции связей.
()
ki
i
i
A
Q
q
δ
δ
=
i
i
П
Q
q
∂
=−
∂
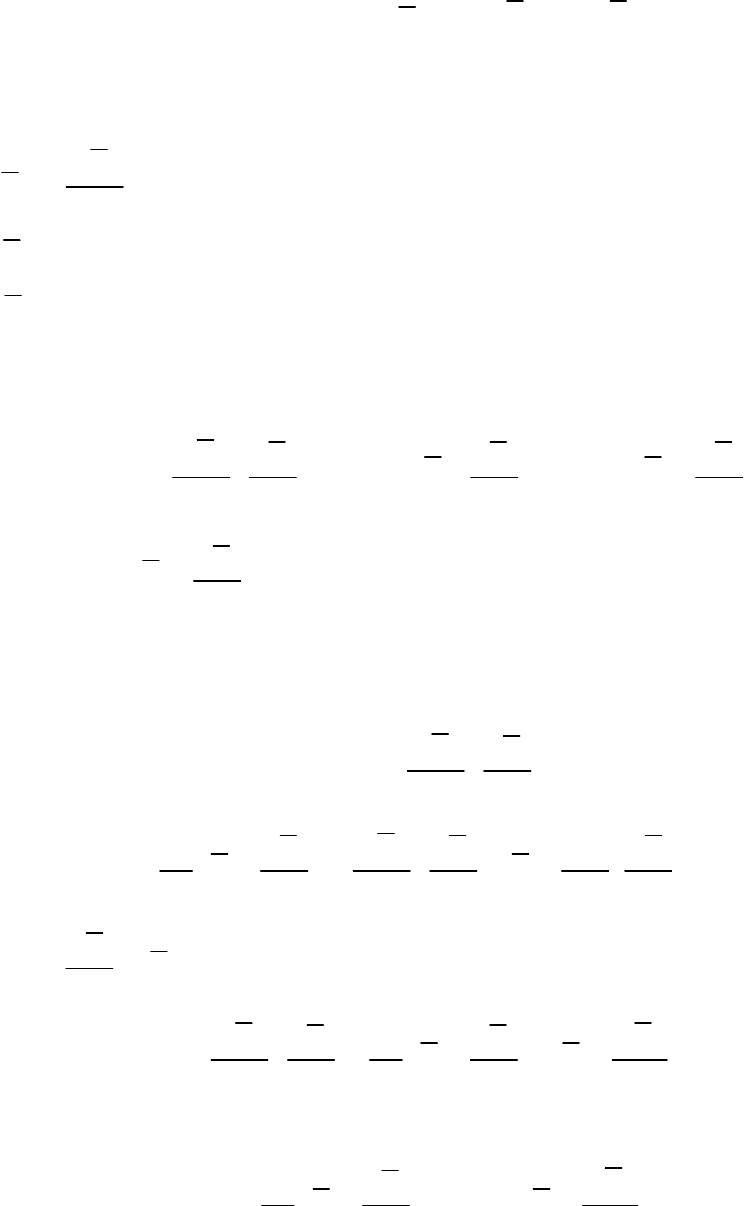
266
Запишем основное уравнение динамики для системы:
111
nnn
kk k k
kkk
mFN
===
=+
∑∑∑
a , (8)
где m
k
– масса k – той точки системы;
k
k
d
dt
v
=a - абсолютное ускорение точки;
k
F - активная сила;
k
N - реакция связи.
Левую и правую части равенства (8) умножим на выражение (5)
и получим:
111
nnn
kk k k
k ikiki
ii i
kkk
dr r r
mqFqNq
dt q q q
v
δ
δδ
===
∂∂∂
⋅=⋅+⋅
∂∂∂
∑∑∑
.
Но
1
()
0
n
N
k
kiki
i
k
r
NqA
q
δδ
=
∂
⋅==
∂
∑
, так как связи в системе иде-
альные.
При
δ
q
i
≠
0 можно записать
1
n
kk
ki
i
k
dr
mQ
dt q
v
=
∂
⋅
=
∂
∑
. (9)
Найдем
() ()
kkk k
kk
iii
drdr dr
dt q dt q q dt
v
vv
∂∂∂
⋅=⋅+⋅
∂∂∂
.
При
k
k
dr
dt
v= , с учетом соотношения (2), находим
()
kk k k
kk
iii
drd r
dt q dt q q
vv
vv
∂∂∂
⋅= ⋅ −⋅
∂∂∂
.
Полученную величину подставим в уравнение (9). Тогда
11
()
nn
kk
kk kk i
ii
kk
dr
mmQ
dt q q
v
vv
==
∂∂
⋅
−⋅=
∂∂
∑∑
.
267
Вынесем
d
dt
,
i
q
∂
∂
и
i
q
∂
∂
за знак суммы, тогда получим:
22
11
11
()()
22
nn
kk kk i
ii
kk
d
mmQ
dt q q
vv
==
∂∂
−
=
∂∂
∑∑
.
Но
2
1
1
2
n
kk
k
mTv
=
=
∑
- кинетическая энергия механической системы
как функция обобщенных координат и обобщенных скоростей.
Окончательно запишем
(
1,is= ). (10)
Уравнения (10) являются дифференциальными уравнениями
движения голономной механической системы в обобщенных коор-
динатах или уравнениями Лагранжа второго рода.
5. Структура уравнений Лагранжа второго рода
Окончательный вид уравнений (10) определяется зависимостью
кинетической энергии системы от обобщенных координат и скоро-
стей и силами, действующими на систему. Количество уравнений
(10) определяется числом степеней свободы s механической сис-
темы.
При составлении каждого уравнения Лагранжа (10) необходимо:
1. В механической системе показать обобщенные координаты,
количество которых зависит от числа степеней свободы системы, а
также обобщенные скорости каждой материальной точки системы.
2. Через обобщенные координаты и обобщенные скорости вы-
числить кинетическую энергию системы и привести ее к виду (3)
или (4).
3. Вычислить частную производную от кинетической энергии по
обобщенной скорости.
i
ii
dT T
Q
dt q q
∂
∂
−
=
∂∂
268
4. Вычислить полную производную по времени от полученного
выражения, в которую войдут обобщенные ускорения
q
i
, обоб-
щенные скорости
q
i
, обобщенные координаты q
i
и параметр t для
реономных связей.
5. Вычислить частную производную от кинетической энергии по
обобщенной координате.
6. По формуле (6) вычислить обобщенные силы. При этом по-
лагать
δ
q
1
≠
0 при вычислении Q
1
, а
δ
q
2
= 0, . . . ,
δ
q
s
= 0.
В результате система уравнений Лагранжа второго рода пред-
ставляет собой систему из n обыкновенных линейных или нели-
нейных дифференциальных уравнений второго порядка относи-
тельно обобщенных координат.
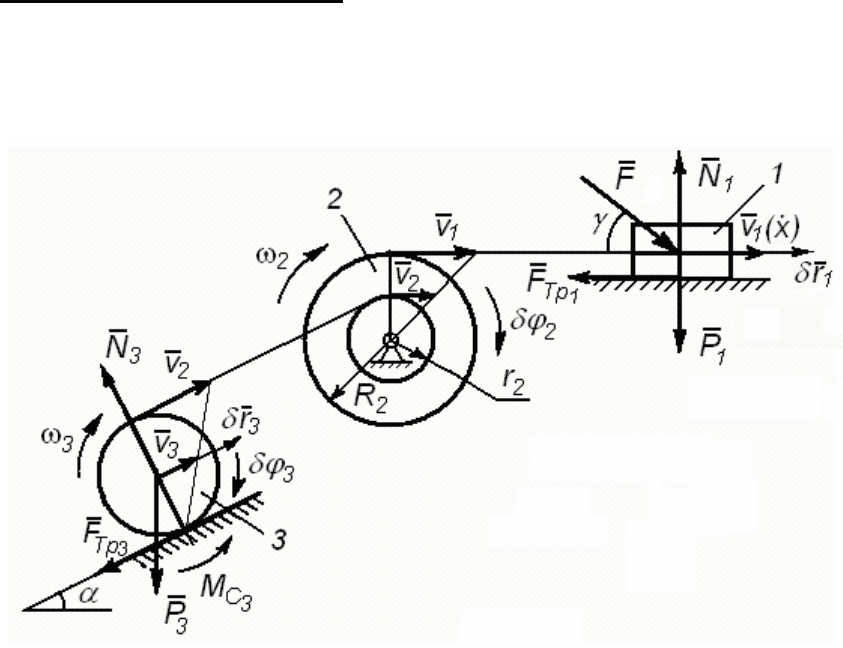
Пример решения задачи
Механическая система (рис. 174) с одной степенью свободы со-
стоит из трех тел, соединенных между собой нерастяжимыми ни-
тями.
Рис. 174
269
Дано:
321
m,m,m - массы тел;
223
,,rRr - радиусы тел; F - ак-
тивная сила;
a
,
g
- углы;
r
2
- радиус инерции тела 2; f - коэффици-
ент трения скольжения тела 1;
k - коэффициент трения качения те-
ла 3.
Определить ускорение тела 1 (
1
a ).
Решение
В качестве обобщенной координаты выбираем перемещение
тела 1 –
x. Тогда qx= . Для этой координаты запишем уравнение
Лагранжа второго рода.
dT T
Q
dt x x
∂
∂
−
=
∂
∂
.
Вычисляем кинетическую энергию механической системы
321
TTTT
+
+
= , если
1
x
v
=
.
Тело 1 -
22
111 1
11
22
Tm mxv==
- поступательное движение.
Тело 2 -
2
222
1
2
T
ω
=
I
- вращательное движение.
При
2
222
Im
ρ
= ,
1
2
22
x
RR
v
ω
==
,
2
2
2
22
2
Tm x
R
ρ
⎛⎞
=
⎜⎟
⎝⎠
.
Тело 3 -
22 2
33333 33
113
224
Tm mvv
ω
=+=I - плоское движение
сплошного цилиндра 3.
При
22
31
22
22
rr
x
RR
vv==
,
2
2
2
33
2
3
16
r
Tm x
R
⎛⎞
=
⎜⎟
⎝⎠
.
Окончательно
22
2
22
12 3
22
131
282
2
r
Tmm m x
RR
x
ρ
⎡⎤
⎛⎞ ⎛⎞
⎢⎥
=+ + =
⎜⎟ ⎜⎟
⎢⎥
⎝⎠ ⎝⎠
⎣⎦
a ,
