Теоретическая механика - теория, задания и примеры решения задач
Подождите немного. Документ загружается.

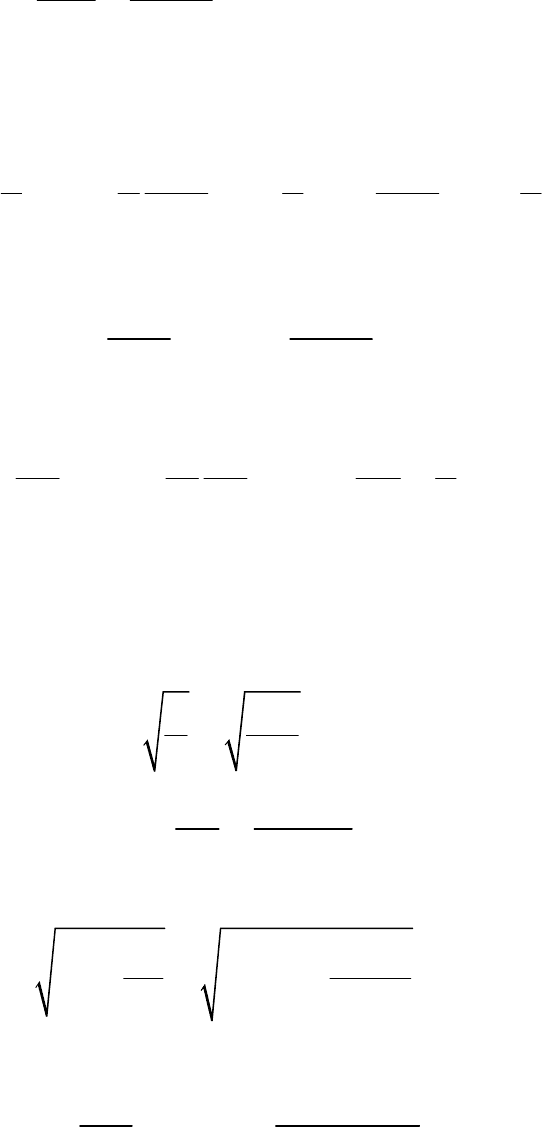
300
Откуда
1
1
29,8
0,049
400
ст
mg
м
c
⋅
== =
λ
.
Статическая деформация пружины
0,049
ст
м
=
λ
.
Запишем квадратичную функцию потенциальной энергии
22 22
66
11
11
11 1 1
()
24 22 2
mg mg
П c
yy
c
y
c
y
=− =− =
ll
.
Здесь
c - обобщенный коэффициент жесткости равен
6
1
1
69,8
400 351 /
220,6
mg
cc Нм
⋅
=− = − =
⋅l
.
Полученные значения подставим в уравнение Лагранжа.
1
;;
2
TdT П
y
c
y
ydty y
y
∂∂∂
===
∂∂∂
aa .
0cy
y
+
=
a
.
Нормальный вид
2
0yky+=
, откуда круговая частота свобод-
ных колебаний
1
351
7,08
7
c
kc
−
== ≅
a
.
Период колебаний
223,14
0,89
7,1
π
Tc
k
⋅
== = .
Определяем амплитуду колебаний по формуле
2
2
22
0
0
22
0, 2
0,02 0,035
7,08
y
Ay м
k
=+= + =
.
Сдвиг фазы колебаний
0
0
7,08 0,02
0,62
0, 2
ky
arctg arctg
р
ад
y
⎛⎞
⋅
⎛⎞
== =
⎜⎟
⎜⎟
⎝⎠
⎝⎠
γ
.
Окончательно запишем уравнение свободных колебаний меха-
нической системы
0,035 sin(7,08 0,62) ( )ytм=+.
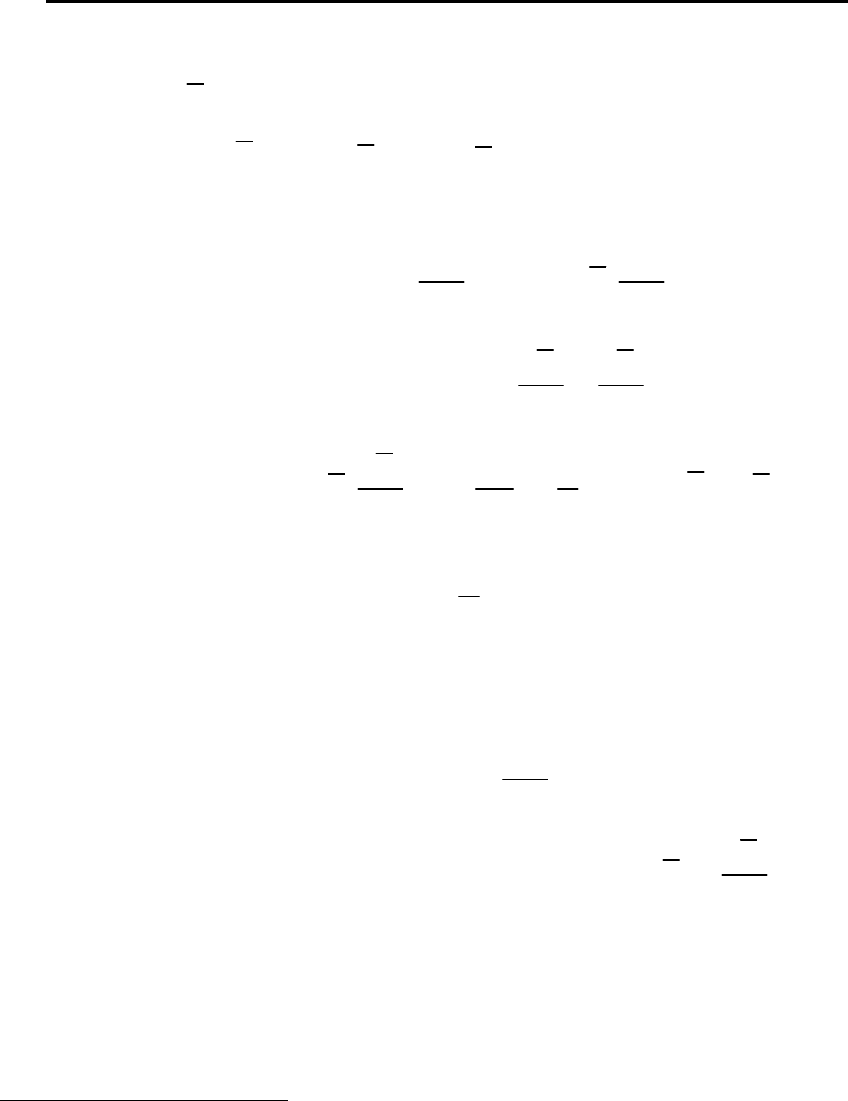
301
2.Свободные колебания механической системы с
учетом сил сопротивления (затухающие колебания)
2.1.Линейное сопротивление и диссипативная функция
Рассмотрим случай линейного сопротивления, когда силы со-
противления
k
R точек системы линейно зависят от скоростей этих
точек.
kkkkk
Rrv
µ
µ
=− =−
.
Обобщенная сила сопротивления
11
.
nn
kk
ck kk
kk
rr
QR µr
qq
=
=
∂
∂
==−
∂
∂
∑∑
Используя тождество Лагранжа
kk
rr
qq
∂
∂
=
∂
∂
, получим
2
11
1
,
()
2
nn
k
ckk kkkk
kk
r
Qr r
qq
vv
µµ
==
⎛⎞
∂∂
=− =− =
⎜⎟
∂∂
⎝⎠
∑∑
.
Введем обозначение
2
1
1
.
2
n
kk
k
Ф v
µ
=
=
∑
Функцию
Ф называют диссипативной функцией или функцией
Рэлея
1
.
Тогда
c
Ф
Q
q
∂
=−
∂
. (4)
Выразим
Ф через q и q
; при )q(rr
kk
=
и
k
k
r
rq
q
∂
=
∂
, будем
иметь
1
Рэлей (Стретт), Джон Уильям, лорд (12.11.1842 – 30.06.1919). Английский
физик. Основные работы по механике относятся к теории колебаний, одним из
основоположников которой он является.

302
2
22 2
11
11 1
22 2
nn
k
kk k
kk
r
Ф
µ
rqµ Bq
q
==
⎛⎞
∂
== =
⎜⎟
∂
⎝⎠
∑∑
.
Разложим функцию
B
в ряд в окрестности положения равнове-
сия системы.
2
2
2
0
0
1
() (0)
2
BB
Bq B q q
q
q
⎛⎞
⎛⎞
∂∂
=+ + +
⎜⎟
⎜⎟
∂
∂
⎝⎠
⎝⎠
"
.
Оставляя в разложении только
(0)Bb
=
, окончательно получим
22
11
(0)
22
Ф Bq bq==
, (5)
где b - обобщенный коэффициент сопротивления.
Подставляя (5) в (4), получим
C
Qbq
=
−
. (6)
2.2 Затухающие колебания
Запишем уравнение Лагранжа в следующем виде:
c
dT П
Q
dt q q
∂
∂
+
=
∂∂
;
где
2
1
2
Tq=
a
- кинетическая энергия,
2
сq
2
1
П =
- потенциальная энергия
Тогда
dT
q
dt q
∂
=
∂
a , cq
q
П
=
∂
∂
, и с учетом (6), получим
qcq bq
+
=−
a .
Полученное дифференциальное уравнение приведем к нор-
мальному виду:
2
20qnqkq
+
+=
; (7)
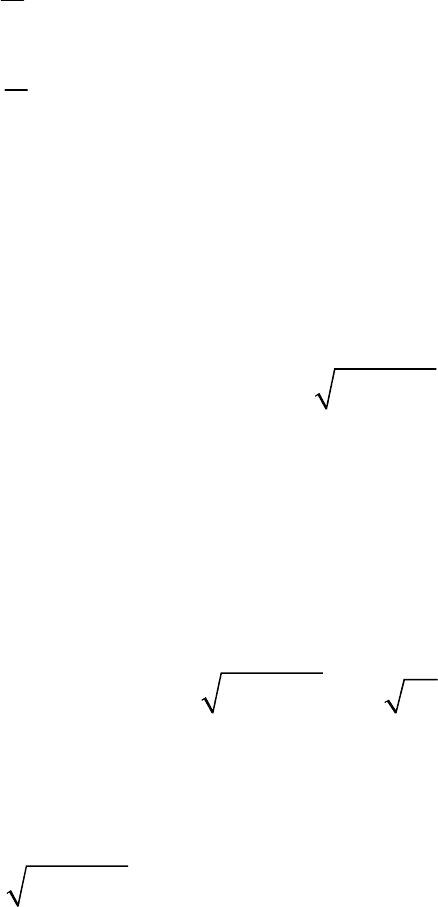
303
где
2
b
n =
a
- удвоенный коэффициент затухания;
2
c
k =
a
- квадрат частоты свободных колебаний.
Мы получили (7) – дифференциальное уравнение затухающих
колебаний системы.
Запишем характеристическое уравнение
22
20snsk
+
+=;
откуда
22
1, 2
snnk
=
−± − . (8)
Корни (8) дают три случая:
1)
<nk
- случай малого сопротивления;
2)
>nk - случай большого сопротивления;
3)
kn =
- случай критического сопротивления.
Рассмотрим случай малого сопротивления, когда
<nk и
(
)
22
1, 2
1snikni=− ± − = − .
Тогда общее решение уравнения (7) запишется в следующем виде
()
(
)
11
''
12 1121
cos sin
ik t ik t
nt nt
qe Ce Ce e C ktC kt
−
−−
=+= +, (9)
где
22
1
kkn=− - частота затухающих колебаний,
12
,CC - произвольные постоянные.
При этом
(
)
1121
cos sin
nt
qneC ktC kt
−
=− + +
()
11 1 2 1
sin cos
nt
eCkktCkkt
−
+− + . (10)
Используя начальные условия
000
0, ,tqq
=
, по уравнениям (9)
и (10), определяем константы
12
,CC.
01
0121
.
qC
qnCCk
=
⎧
⎨
=− +
⎩
304
Откуда
2
1
oo
qn q
C
k
+
=
.
Пусть
11 1
sinCA=
γ
,
21 1
cosCA
=
γ
, тогда
2
22 2
00
112 0
2
1
()qn q
ACC q
k
+
=+=+
,
10
1
1
200
kq
C
tg
Cnqq
==
+
γ
,
10
1
00
kq
arctg
nq q
⎛⎞
=
⎜⎟
+
⎝⎠
γ
.
Окончательно получаем
111
sin( )
nt
qAe kt
−
=+
γ
,
где
1
nt
Ae
−
- огибающая амплитуд затухающих колебаний;
1
γ
- сдвиг фазы колебаний.
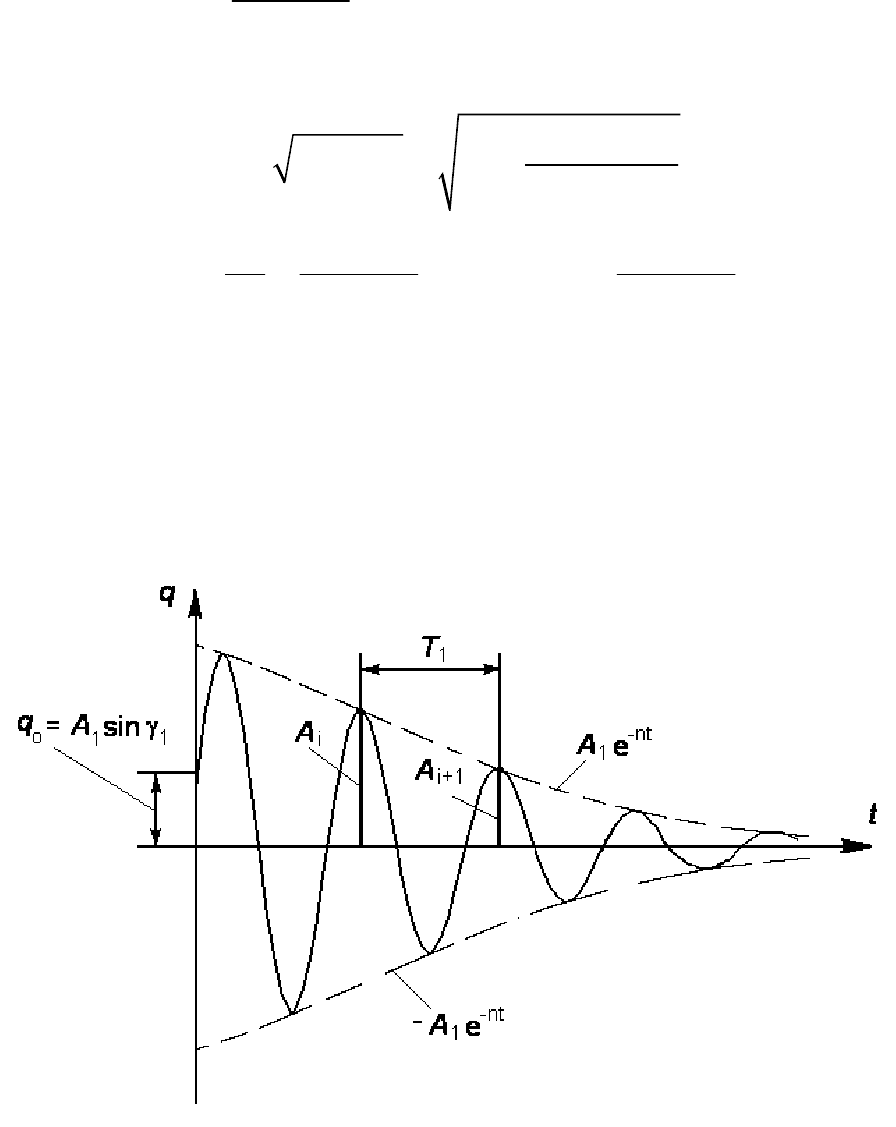
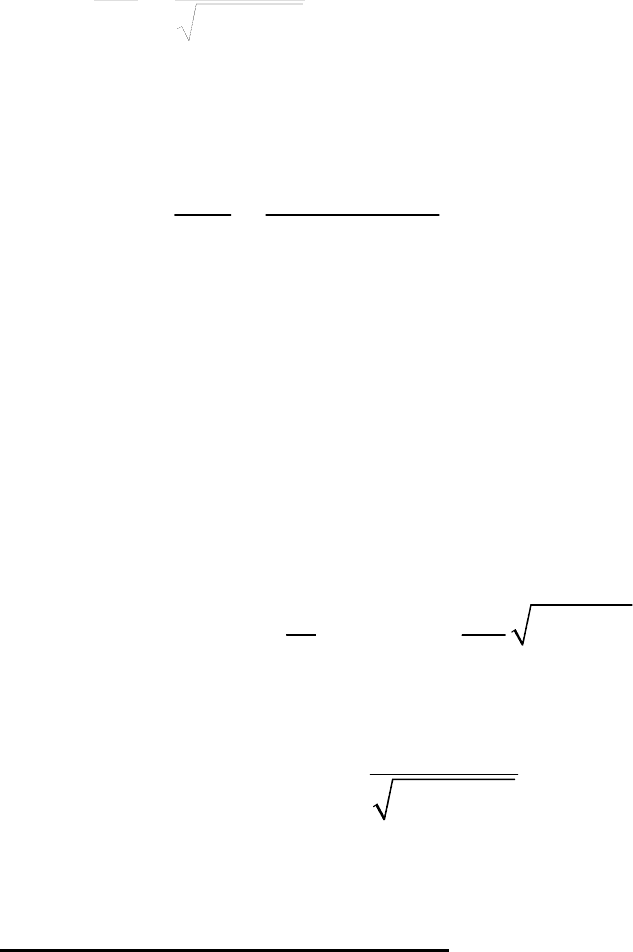
Развертка затухающих колебаний показана на рис. 188.
Рис. 188
На рисунке показаны:
01 1
sinqA
=
γ
- начальное отклонение от
положения устойчивого равновесия системы;
305
22
1
1
nk
2
k
2
T
−
==
ππ
(с) - период затухающих колебаний.
Рассмотрим отношение двух соседних амплитуд через период
1
T ,
1
nt
i
AAe
−
= и
1
()
11
nt T
i
AAe
−+
+
= .
Тогда
1
1
1
1
1
nt
nT
i
nT
nt
i
AAe
e
A
Ae e
−
−
−
+
== =
⋅
δ
.
Величина
1
nT
e
=
δ
будет называться декрементом затухания, а
1
Λ ln nT==
δ
- логарифмическим декрементом затухания.
При этом
Λ находится чисто экспериментальным путем по раз-
вертке затухающих колебаний, если огибающая амплитуд – экспо-
нента.
По известной величине
Λ можно определить коэффициент за-
тухания
n
1
Λ
n
T
=
,
22
Λ
2
nkn
π
=−.
Из полученного уравнения определяем
n
22
Λ
Λ 4
k
n =
+
π
)с(
1
−
. (11)
Зная
n
, находим 2bn= a .
Пример решения задачи Д. 10.2
Для механической системы (рис.187) известны следующие па-
раметры:
1
7,08kc
−
= - частота свободных колебаний; Λ 1, 4= -
логарифмический декремент затухания. Определить уравнение за-
тухающих колебаний системы y=y(t) и коэффициент демпфирова-
ния
β, если
00
0,02 , 0, 2 / .y м y мс
=
=

306
Решение
По формуле (11) определяем коэффициент затухания
1
22 22
Λ 7,08 1, 4
1, 5 3
Λ 41,44
k
n с
ππ
−
⋅
== ≅
++
.
Частота затухающих колебаний
22 2 2 1
1
7,08 1,53 6,93kkn с
−
=−= − = .
Обобщенный коэффициент сопротивления
2 2 1,53 7 21,42 /bn кг с==⋅⋅=a .
Сила сопротивления в демпфере
cE
R
β
V
=
.
3
36
1
0, 2
0,33
0, 6
E
V φ
yy y
=== ≅
l
l
l
.
При этом
cc
RQby==
.
Откуда
0,33b
y
β
y
=
, вычисляем коэффициент демпфирования
21,42
64,91 /
0,33 0,33
b
βкгc
== ≅ .
Запишем дифференциальное уравнение затухающих колебаний.
2
20ynyky
+
+=
.
Общее решение полученного уравнения
111
esin( )
nt
yA kt
−
=+
γ
.
Вычисляем параметры A
1
и γ
1
.
2
2
22
1
22
1
()
(0,02 1,53 0,2)
0,02 0,039 ;
6,93
oo
o
yn y
Ay м
k
+
⋅+
=+ = + =
10
11
0
6,93 0,02
tg 0,601; 0,541
1,53 0,02 0,2
o
ky
р
ад
ny y
⋅
== = =
+⋅+
γγ
.
Окончательно запишем уравнение затухающих колебаний
1, 5 3
0,039e sin(6,93 0,541) ( )
t
ytм
−
=+.
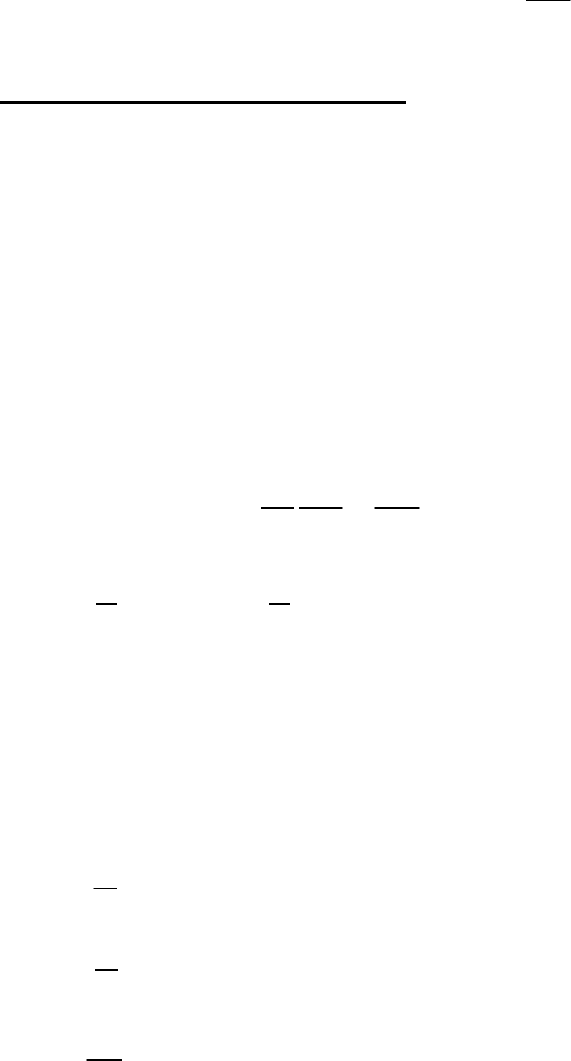
307
Коэффициент демпфирования
64,91
Нс
β
м
= .
2.3 Вынужденные колебания
На консервативную механическую систему, помимо обобщенной
силы сопротивления
,
C
Qby=−
действует обобщенная сила воз-
мущения, которая изменяется по гармоническому закону:
0
sin( )
в
QF ptδ
=
+ ,
где
0
F - амплитуда силы,
p
- частота ее изменения,
δ
- сдвиг фазы
ее действия.
Тогда уравнение Лагранжа запишется в следующем виде
c в
dT П
QQ
dt dq q
∂
∂
+
=+
∂
.
При
2
1
2
Tq=
a и
2
1
2
П cq= будем иметь
0
sin( )qcq bqF ptδ+=−+ +
a .
Полученное дифференциальное уравнение приводим к нор-
мальному виду:
2
2sin()qnqkqh ptδ++= +
; (12)
где
2
b
n
=
a
- двойной коэффициент затухания;
2
c
k =
a
- квадрат частоты свободных колебаний;
0
F
h
=
a
- параметр ускорения.
Решение уравнения (12) ищем в виде
12
qq q
=
+ .
Здесь
1
q общее решение уравнения (12) без правой части, т.е.
2
111
20qnqkq
+
+=
,

308
2
q - частное решение уравнения (12).
Частное решение ищем в виде
2
sin( )qA ptδε
=
+−.
При установившемся движении системы ее колебания будут
только вынужденные
)t(qq
2
2
= .
Рассмотрим этот вид колебаний.
2
sin( )qA ψ - ε
=
,
2
cos( )qAp ψε
=
−
,
2
2
sin( )qApψε=− −
, где ψ pt δ
=
+ , а ψ p=
.
Полученные значения
222
,,qqq
подставим в левую часть
уравнения (12).
22
sin( ) 2 cos( ) sin( ) sinAp ψε npA ψε kA ψε h ψ−−+ −+−=.
Раскроем гармоники
sin
()
,cos
()
ψε ψε
−
− .
22
sin cos cos sin 2 cos cosAp ψεAp ψεnpA ψε−+ + +
22
2 sin sin sin cos cos sin sinnpA ψεkA ψεkA ψεh ψ++−=,
где
()
ψψt= .
Приравняем коэффициенты при
cos , sinψψ
в левой и правой
части полученного равенства
22
22
( ) cos 2 sin
()sin2cos0.
kpA ε npA ε h
kpAε npA ε
⎧
−+=
⎪
⎨
−− =
⎪
⎩
Получаем систему двух алгебраических уравнений с неизвест-
ными величинами
A и .ε
Из второго уравнения находим сдвиг фазы колебаний
ε
22
2np
tgε
kp
=
−
,
22
2np
ε arctg
kp
=
−
. (13)
Если первое и второе уравнения возведем в квадрат и сложим,
то получим
2222 2222
()4kpA npAh−+ =.
Откуда амплитуда вынужденных колебаний определится по
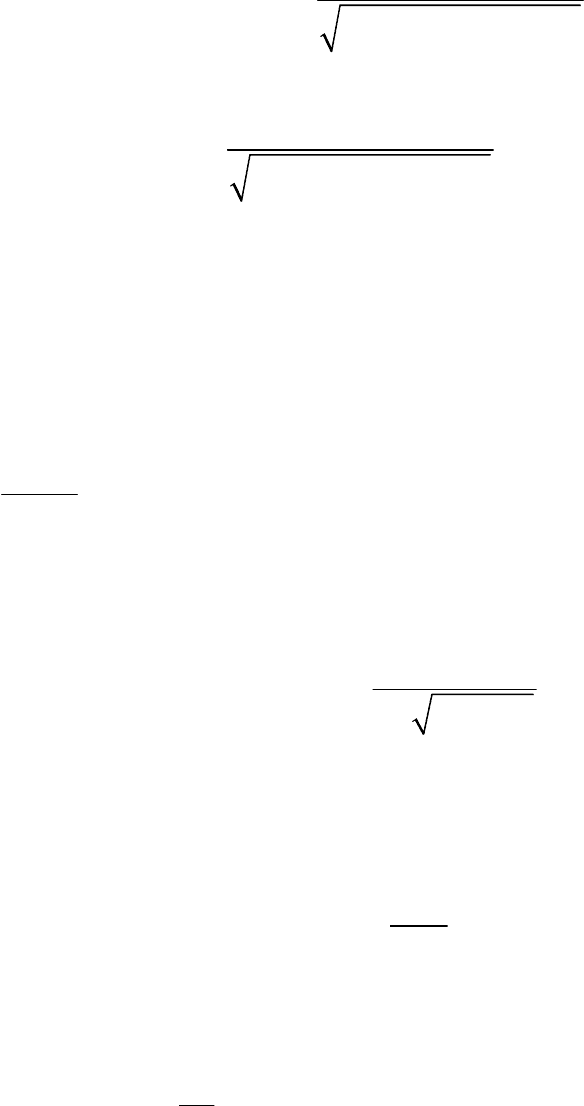
309
формуле
22 22
()4
h
A
kp np
=
−+
. (14)
Окончательно уравнение вынужденных колебаний будет иметь вид
2
22 22
sin( )
()4
h
qptδε
kp np
=+−
−+
.
Определим максимальную амплитуду вынужденных колебаний
.A
max
Рассмотрим подкоренное выражение в уравнении (14) и пред-
ставим, что
.pn4)pk()p(f
22222
+−=
Найдем экстремум этой функции.
22 2
11 1
()
2
()(
2
)
80
df p
kp p np
dp
=−−+ =.
Откуда
22 2 222
11
2, ()4( )
p
kn fp nkn=− = − .
Окончательно получим
max
22
()
2
h
A м
nk n
=
−
. (15)
Если частота свободных колебаний
k будет равна частоте воз-
мущающей силы
p
, то наступает резонанс
)
p
k
(
≈
.
Резонансная амплитуда определяется по формуле
max
<
2
рез
h
AA
np
= . (16)
Как резонансная, так и максимальная амплитуды зависят от ве-
личины коэффициента затухания
n , частоты свободных колебаний
и параметра
0
F
h
=
a
.
