Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

Other considerations on particle dynamics

653

2( )

vgxh=− + ,

(0)hx

− , (0) 0

. (10.2.63')

From (10.2.62'') it results (one introduces the sign minus, taking into account the

zone in which is the particle, Fig.10.15)

() ()

1/2

22 22

312 12

1 1 ...

xl xx l xx

⎡⎤⎡ ⎤

=− − + =− − + +

⎢⎥⎢ ⎥

⎣⎦⎣ ⎦

We assume that the length

l is very large and that the mass m is sufficiently great.

The pendulum has a small displacement from its position of equilibrium

Ω , oscillating

without initial velocity with respect to the Earth; in this case, it effects small oscillations

around the position of equilibrium, which is a stable one. We can thus state that the

ratios

/xl and

/xl are very small (we say, generally, that they are of order of

magnitude

0ε > , that is

/()xl ε

O ,

/()xl ε

O ); it results

(

)

1xl ε=− +

⎡⎤

⎣⎦

O ,

(

)

1hl ε=− +

⎡

⎤

⎣

⎦

O and

(

)

hx ε+=O . From (10.2.62''),

(10.2.63'), we can write

++=

11 22 3 3

0xx xx xx

222

123 3

2( ) ()xxx ghx ε++=− + = O ,

so that

()x ε

 O ,

()x ε= O ,

()x ε

 O ,

(

)

33 11 22

///xx l xx l xx l ε=− − =O

and then

(

)

x ε= O . The tension T being of the order of unity, the first two

equations (10.2.62') show that we have at least

()x ε

 O ,

()x ε= O .

Differentiating the relation (10.2.62'') once more with respect to time, we can write

(

)

(

)

222 2

3 3 123 1 1 2 2

(/) / (/) (/)xlx x x x l xlx xlx ε=− + + − − =      O , so that

x

()ε= O . Using the previous evaluations and observing that, in this case,

xl≅− , the

third equation (10.2.62') leads to

Tmg

≅

, (10.2.64)

the tension in the thread being approximately equal to that corresponding to the position

of equilibrium.

Returning to the first two equations (10.2.62'), we find the equations of motion in the

plane

− , tangent to the position of equilibrium Ω (which corresponds to small

oscillations around this stable position of equilibrium), in the form (we consider the

axes

xΩ and

xΩ parallel to the axes

Ox and

Ox , respectively; for the sake of

simplicity, we use the same notations for the co-ordinates)

112

2sin

xxx

ωλ=− +  ,

221

2sin

xxx

ωλ=− −  ; (10.2.65)

in a vector form, we get

−− ×

 

ρωρ, (10.2.65')

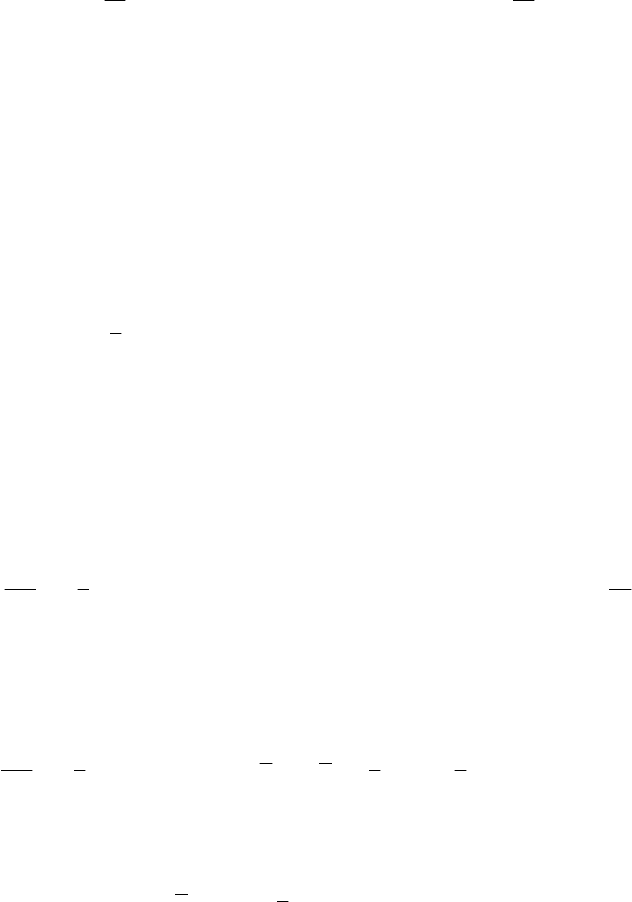
MECHANICAL SYSTEMS, CLASSICAL MODELS

654

where

333 3

sinωωλ

=iiω is the vector component of the rotation vector ω along

the local vertical, while

ρ is the position vector in the tangent plane. A vector product

ρ leads to (we have

0⋅=ρω )

()

333

2( ) 2( )

ddtt

ρ×= × =− × × =− ⋅ =−

   

ρρ ρρ ρ ω ρ ρρω ω,

wherefrom

ρ×+ =



ρρ ω

const=

JJJJG

C , (10.2.66)

corresponding to a first integral of moment of momentum; scalarly, we have

(

)

12 21 1 2

sinxx xx x x Cωλ−++ =

, constC

. (10.2.66')

In polar co-ordinates

,ρθ, we may express the first integrals (10.2.63'), (10.2.66') in the

form

(

)

222

2( )

gl h

ρθρ++ = −



sin Cρθ ρω λ



, (10.2.67)

characterizing thus the motion in the plane

xxΩ .

We introduce a system of axes

Ωξ ξ , movable with respect to the system

xxΩ ,

which is rotating about the local vertical

Ox with the angular velocity

sinωλ−=− iω (in the sense north-east-south-west, hence clockwise). Taking into

account (10.2.1), (10.2.1') and starting from the equation (10.2.65'), we can write the

equation of motion of the particle

P with respect to this last movable frame in the form

[]

33 33 3

2()()()2()

∂∂

=−− ×−−×−−×−×−−×

∂



ρρ

ρωρ ω ρ ω ω ρ ω

where

/ t∂∂ρ and

/ t∂∂ρ are the relative velocity and acceleration, respectively. We

notice that



0ω and

d/d / ( )tt

=∂ ∂ + − ×



ρρ ωρ, so that (we have

0⋅=ρω )

()

∂

=− + × × =−

∂

ρω ωρ ρ,

222

sin

ωωωλ=+ =+ . (10.2.68)

This is the equation of motion of a particle

P of mass m , attracted by the centre Ω

with an elastic force

(

)

sin

ωωλ−=−+

ρ ; (10.2.68')

Other considerations on particle dynamics

655

hence, the trajectory is an ellipse or a segment of a line (degenerate ellipse), fixed with

respect to the frame

Ωξ ξ (Fig.10.16). This ellipse is rotating with respect to the frame

xxΩ , linked to the Earth, about the local vertical, with the angular velocity

sinωωλ= , in the sense east-south-west-north (clockwise); hence, if the particle

pendulates in the plane

xPΩ , then this plane is rotating with the angular velocity

in the sense indicated above.

Figure 10.16. The Foucault pendulum. Elliptic trajectory in the tangent plane with

respect to the non-inertial frame of reference

Ωξ ξ .

If we change the variable

tθψω

− and notice that (because (/)t×∂ ∂ρρ

ρψ=



i , Fig.10.16)

(

)

(

)

(

)

22222

33 33

()2,, 2

dtt t

ρρω ωρψ

∂∂

=+×+ =++

∂∂



ρρ ρ

ρω ωρ

then we can express the first integrals (10.2.67) with respect to the frame

Ωξ ξ in the

form

(

)

222 22 2

sin 2 ( )

gl h

ρρψ ω λρ+++ =−



 ,

Cρψ



; (10.2.67')

we took into account that

()

22 22 8 7

sin 1 sin 1 10 ...10

gglg

llgl

ωλ ωλ

−−

⎛⎞

+=+ =+

⎡

⎤

⎜⎟

⎣

⎦

⎝⎠

O ,

in the first integral, as it will be seen further. As a matter of fact, by calculation it has

been obtained the term

(

)

22 2

/2singl ωλρ+ ; but by the mentioned approximation

MECHANICAL SYSTEMS, CLASSICAL MODELS

656

one has obtained a result corresponding to the elastic force (10.2.68'). Considering the

elastic force of the form

(/)mg l−

, we write the first integral

222 2

2( )

gl h

ρρψ ρ

+=−



 , (10.2.67'')

correspondingly. We have thus put into evidence the first integral of energy (the

potential energy corresponds to the conservative elastic force (10.2.68')) and the first

integral of areas.

The particle is launched from a position of rest

, of position vector

ρ (situated on

the

xΩ

-axis, because for

we have θψ

), with a zero initial velocity with

respect to the frame

xxΩ

linked to the Earth ( d/dt

, hence d/d 0tθ = for

0t =

); in case of a change of variable of the form

tθψω ϕ

−−

constϕ =

, we

start from an initial position

non-situated on the

xΩ

-axis. If

PxΩ∈

, then we

get

(0)ψω=



, so that the constant of areas is given by

sinC ρω ρω λ==

. The

initial velocity is

000

(/)t=∂ ∂ = ×v

ωρ, normal to

and of magnitude

(

)

000

sinv ωρ ρω λ ρψ== =



(Fig.10.16); it results, as well, (0) 0ρ = .

Analogously, one obtains the energy constant

222

/2 /hl l gρρω=− − . The first

integrals (10.2.67') become thus

(

)

()

222 222 22

ρρψ ωρρ ρω+++ −=



ρψ ρω=



. (10.2.67''')

We notice also that the initial position is one of the extremities of the major axis of the

elliptic trajectory. The ellipse is travelled through by the particle in an opposite

direction to that of the rotation of the frame

Ωξ ξ with respect to the frame

xxΩ

(counterclockwise).

In contradistinction to Foucault’s pendulum, in case of the spherical pendulum, (see

Chap. 7, Subsec. 1.3.7), in the hypothesis of small oscillations, the elliptic trajectory is

fixed; but, in general, the particle oscillates between two parallel circles, while the first

integral of areas shows that the meridian plane of the pendulum is rotating about the

vertical in the direction indicated by the initial velocity, which is the same with that in

which the movable ellipse, which approximates the projection of the particle on the

tangent plane

xl=− is travelled through. This result is obtained because the spheric

pendulum is considered with respect to a local (inertial) frame; but Foucault’s

pendulum is studied with respect to a local frame, considered to be non-inertial, taking

thus into account the influence of the Coriolis force.

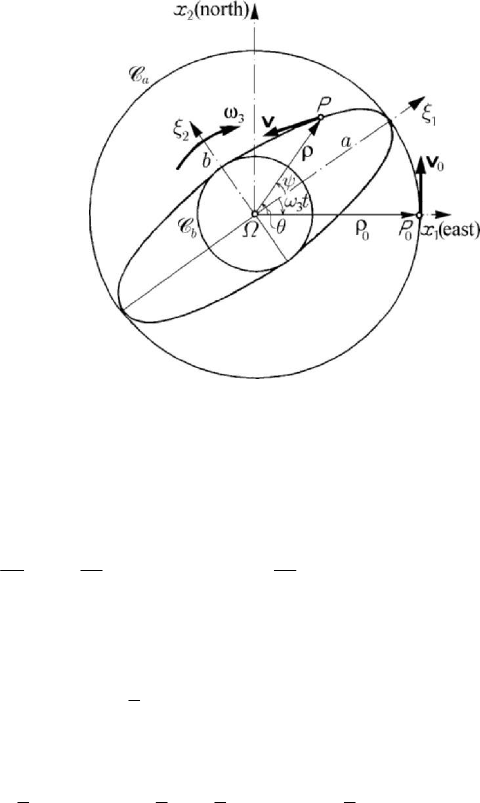
In case of Foucault’s pendulum, the semiaxes of the ellipse are

a ρ= ,

ρω ρω

ρω

== ≅

; (10.2.69)

the ratio

Other considerations on particle dynamics

657

=≅

(10.2.69')

is, in general, very small, and the eccentricity

()

1/2

287

1 1 1 ... 1 10 ...10

bl l

−

−−

⎛⎞

=−=+ =− +=−

⎜⎟

⎝⎠

O (10.2.69'')

is smaller than the unity, but very close to it.

The ellipse is travelled through in a period

ππ

τπ

== ≅

(10.2.70)

and effects a complete rotation north-east-south-west (clockwise) in an interval of time

equal to

sin

ππ

ωωλ

. (10.2.70')

From (10.2.69')-(10.2.70') it results

(10.2.71)

and we can state

Theorem 10.2.13 (Chevilliet). In the motion of Foucault’s pendulum, the ratio of the

two semiaxes (minor and major) of the ellipse of projection is equal to the ratio of the

period in which the ellipse is travelled through to the period of complete rotation of it.

Figure 10.17. The Foucault pendulum. The trajectory with respect to the inertial frame of

reference

Ox x

if 0ψ

≠



(a) and if 0ψ



(b), for 0θ



At the points for which

0ρ

 , the velocities are normal to the corresponding radii

vectors, the trajectory being normal to those radii and tangent to the circles with

Ω as

MECHANICAL SYSTEMS, CLASSICAL MODELS

658

centre, having as radii the above mentioned ones; if we make

0ρ

 in (10.2.67''') and

eliminate



, then we find again the semiaxes a and b given by (10.2.69). Indeed, in

its rotation, the ellipse is contained between the circles

C and

C of radii a and b ,

respectively. One observes that the semi-major axis

a does not depend neither on the

location on the Earth surface, nor on the initial conditions; but the semi-minor axis

depends on the latitude

λ , as well as on the initial conditions (radius

ρ ). Moreover,

the initial conditions play an important rôle, specifying the nature of the trajectory of

the particle with respect to the frame

Ωξ ξ (segment of a line or ellipse) and with

respect to the frame

xxΩ . Thus, for

ρρ

we obtain

ψω=



, hence 0θ =



, while

/ρρωω= leads to

(

)

333

///glψωω ω ω==+



, wherefrom

/glθω=



. The

trajectory of the particle with respect to the frame

xxΩ can be represented as in

Fig.10.17,a; the points of tangency to the circle

aρ

are cuspidal points ( 0θ =



while at the points for which

min

ρρ

the trajectory is tangent to the circle

bρ =

(

0θ ≠



). If 0ψ =



, then 0C

and the trajectory is a segment of a line, with respect

to the frame

Ωξ ξ ; hence, we get

θω

−



, the trajectory with respect to the frame

xxΩ having the form of a multifolium (in particular, quadrifolium) (Fig.10.17,b). In

case of other initial conditions (if

d/d 0tθ

≠

for 0t

) one obtains trajectories as in

Figs 10.18,a,b.

Figure 10.18. The Foucault pendulum. Trajectories with respect to the inertial

frame of reference

Ox x

for 0θ

≠



The numerical data in Foucault’s experiment have been

2.8 10 gm =⋅ and

6.7 10 cml =⋅ , Paris’ latitude being 48 50λ

′

° to which corresponds

9.809 10 cm/sg =⋅ ; from the formulae (10.2.70), (10.2.70') it results 16.42 sτ = ,

114458 s 31 hours 47 min 38 s 32 hoursT == ≅. These theoretical data have

been in very good concordance with the experiment; at the same time, the quantitative

evaluations previously made are justified. A thorough study can be found in the

dissertation of H. Kamerlingh Onnes (Groningen, 1879). In Cologne, at the latitude

Other considerations on particle dynamics

659

50 50 30λ

′

′′

=°

, Garthe has obtained (with

510 cml

⋅ ,

1.7 10 gm =⋅ and

310 cmr =⋅ ) a rotation of 11 38 51

′

′′

, the rotation observed experimentally being

11 37 40.8

′

′′

(hence, a very good concordance). In Bucharest, at the latitude

45λ =°, one obtains 121854 sT ≅ 33 hours 50 min 54 s

34 hours

≅

In the austral hemisphere, the ellipse is rotating in the sense east-north-west-south

(counterclockwise).

Because the theoretical results obtained starting from the hypothesis of rotation of

the Earth about the poles’ axis are in good concordance with the experimental ones, we

can state that the Earth is indeed rotating about this axis; moreover, the universal

attraction law which has been put in evidence – at the beginning – for cosmic bodies,

extends its validity for the phenomena at the Earth surface too. We mention that an

observer localized in an inertial frame (e.g., a heliocentric frame) would see the

pendulum oscillating only in the same plane (assuming that the trajectory of the particle

with respect to the frame

Ωξ ξ is a segment of a line), the Earth being in rotation with

respect to this plane.

These conclusions have a particular importance for the knowledge of our planet and

put in evidence the interest presented by Foucault’s experiment. We must mention also

that the motion of rotation of the Earth has been stated by astronomical observations,

before this famous experiment; but Foucault’s study puts theoretically in evidence the

motion of the Earth, astronomical observations being no more necessary (which cannot

be made if, for instance, the Earth would be covered by a thick stratum of clouds, as

Venus, the only planet which is rotating about its axis from west to east).

3. Dynamics of the particle of variable mass

There exist bodies the mass of which is variable in time; it can decrease (e.g., the

mass of a rocket, which is acted upon by a propulsive force due to the ejection of an

explosive material – fine particles, gas, internal liquid – emission phenomenon) or

increase (e.g., a planet on which fine cosmic particles of a nebula encountered in its

way are falling – capture phenomenon). We may consider also other examples, as: an

aerostat which lifts by throwing down the ballast over the border, the splinting of a

device processed at the lathe etc. In the case in which such a body can be modelled as a

particles arises the problem to obtain the equation governing this motion and to

integrate it in various particular cases.

3.1 Mathematical model of the motion. General theorems

To can set up a mathematical model of motion of a particle of variable mass, hence

to find a law of motion which may be reduced to Newton’s equation in case of a

constant mass, we start from a classical mathematical model, corresponding to a

discrete mechanical system, the general theorems (especially, the theorem of

momentum) allowing then to establish the equation of motion which is governing the

considered mechanical phenomenon. We may then state the corresponding general

theorems, which extend those of the particle of constant mass.

MECHANICAL SYSTEMS, CLASSICAL MODELS

660

3.1.1 Meshcherskiĭ’s model. Levi-Civita’s equations

We assume, in what follows, that the motion of a free particle

P of variable mass

()mmt= takes place by the detachment (emission) of some parts of it (it corresponds

the decrease of the mass); this phenomenon puts in evidence the apparition of internal

forces, which are called reactive forces. We assume thus that, at the moment of

detachment of some parts of the particle (in fact, the particle

P is a mechanical system

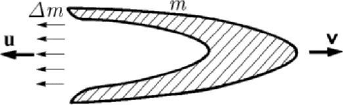
Figure 10.19. Meshcherskiĭ’s mathematical model of a particle of variable mass.

which is emitting particles, e.g., a rocket which is emitting particles of gas, Fig.10.19),

takes place a phenomenon analogous to that of collision. We consider the motion of the

particle with respect to an inertial (fixed, absolute) frame of reference, so that – at the

moment

t – it has the velocity ()tv and the momentum () ()tmt

Hv. In the

interval of time

tΔ , a part of mass m

−

Δ , 0m

> , is detached from the particle, with

the absolute velocity

u and with a relative velocity w with respect to a non-inertial

frame of reference, attached to the particle in motion; on the basis of the principle of

action and reaction, appears a reactive force

R (corresponding to a collision force in

the mentioned analogy). The momentum of the system formed by the particle without

the detached part (after emission) and the detached (emitted) part (see Chap. 11,

Subsec. 1.1.1) is given by

[

]

() ()( )tt m m m

′

Δ= −−Δ +Δ −ΔHvvu, where

′

Δ v

represents the variation of the velocity of the particle

P of variable mass, in the

interval of time

tΔ , due to the process of emission of a part of it. The considered

mechanical system is a closed one, so that we can apply the conservation theorem of

momentum (see Chap. 11, Subsec. 1.2.5), hence

()()mm mm

′

Δ+Δ−Δ=vvu v.

Neglecting the terms of higher order, we obtain

(/)( )mm

′

=Δ −vuv, determining

thus the variation of the velocity of the particle of variable mass

m , due to the emission

of mass

−

Δ . Introducing the influence of the given forces of resultant F too,

Newton’s equation gives

(/ )mt

′

Δ= Δ

vF . Finally, on the basis of parallelogram’s

principle, we may write

′

′′

Δ=Δ +Δvvv

, so that, dividing by t

and passing to the

limit for

→ , it results I.V. Meshcherskiĭ’s equation (we assume that, in the

interval of time

tΔ , the velocity v of the particle P has a continuous variation and is

not influenced by the collision effect due to the emission of mass, taking into account

the inertia of the mass of the particle and that, before the emission, the emitted mass had

the same velocity as the particle

)

()mm

+−



vF uv, 0m

 , (10.3.1)

obtained by him in 1897; it was found again in 1898 by K.E. Tsiolkovskiĭ and applied

to the study of the rockets with several steps. We can write this equation also in the

form

Other considerations on particle dynamics

661

()

==+



vHF u, 0m

 . (10.3.1')

Observing that the relative velocity of the emitted part with respect to a non-inertial

frame of reference, attached to the particle in motion, is given by

=−wuv, we can

introduce the reactive force

()mm

−=Ruvw, 0m

 , (10.3.2)

so that Meshcherskiĭ’s equation takes the form



vFR, 0m

 ; (10.3.1'')

we state thus (with respect to an inertial frame of reference)

Theorem 10.3.1 (Meshcherskiĭ). The product of the mass of a free particle of variable

mass by its acceleration is equal to the sum of the resultant of the given forces and the

reactive force which acts upon the particle.

In the case in which the mass of the particle

is increasing, due to a phenomenon

of capture of a mass

mΔ

, we can make an analogous study. Maintaining the

previous notations, we may write

()tm m

+ΔHvu, corresponding to the system

formed by the particle

and the mass

which is captured; as well, we have

()( )( )tt mm

′

+Δ = +Δ +ΔHvv. Using once more the conservation theorem of

momentum and the principle of the parallelogram and passing to the limit, it results

m=+



HF u

, 0m > , (10.3.3)

as well as

mm=+ =+



vF wFR, 0m > , (10.3.3')

the Theorem 10.3.1 remaining still valid.

In the study of capture of meteorites by a planet, T. Levi-Civita assumed that the

absolute velocity

u of the captured masses vanishes (the absolute quadratic mean

velocity of the captured cloud of particles is negligible with respect to the velocity of

the planet); the equation (10.3.3) becomes

()



vHF

, 0m > , (10.3.4)

obtaining thus Levi-Civita’s equation. We may state

Theorem 10.3.2 (Levi-Civita). If the absolute velocity of the masses captured by a free

particle of variable mass vanishes, then we can express the theorem of momentum as in

the case of a particle of constant mass.

The theorem is valid also in the case of emission of mass.

Analogously, if the relative velocity

w of the emitted masses vanishes (uniform

emission of particles in all directions, from a celestial body), then the equation (10.3.1'')

becomes

MECHANICAL SYSTEMS, CLASSICAL MODELS

662



, 0m

 , (10.3.5)

and we can state

Theorem 10.3.3 (Levi-Civita). If the masses emitted by a free particle of variable mass

have a vanishing relative velocity with respect to it, then Newton’s equation of motion

maintains its form.

Projecting Meshcherskiĭ’s equation on the co-ordinate axes, we get

iii

mx F R

+ , 1, 2, 3i

. (10.3.1''')

In particular, if the relative velocity of the masses emitted by the particle

P of

variable mass is directed along the tangent of unit vector

to its trajectory, the

magnitude of the velocity of the particle being constant in time, we can write (the

velocity

w is opposite to the velocity v )

mmwm

=− =−





vF F vτ ,



. (10.3.6)

Often, by a convenient change of variable, we may obtain remarkable forms for the

above equations. Let us suppose, for instance, that the absolute velocity

of the

masses emitted by a particle of variable mass vanishes. Meshcherskiĭ’s equation

(10.3.1) takes the form

−



vF v, (10.3.4')

corresponding to Levi-Civita’s equation (10.3.4). By the change of variable

()

= , (10.3.7)

we get, successively,

d1d

ddtmτ

222

d1d

=− +

 rr

;

replacing in the equation (10.3.3'), we can write, finally,

()

, (10.3.7')

obtaining thus an equation of motion, which has a form analogous to that of the

classical Newton equation.

3.1.2 Meshcherskiĭ’s generalized equation

In some cases, the motion of the free particle

of variable mass takes place with

simultaneous emission and capture of mass. We mention thus the turbo-jet airplanes