Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

Other considerations on particle dynamics

623

Dividing the relation (10.2.15) by

dt , we get

rrr r

TP P

∂

===⋅=+⋅

∂



Fv Fv

(10.2.16)

so that we may state

Theorem 10.2.6' (theorem of kinetic energy; second form). The derivative with respect

to time of the kinetic energy of a free particle in a non-inertial frame of reference is

equal to the power of the relative force which acts upon it in this frame (the sum of the

power of the resultant of the given forces which act upon the particle and the power of

the transportation force).

In case of a particle subjected to bilateral constraints, we apply the axiom of

liberation of constraints and introduce the constraint force

R ; the formulae (10.2.11),

(10.2.12), (10.2.14) - (10.2.16) take the form

∂

==+=+++

∂



HFRFFFR

, (10.2.11')

∂

==×+=+×++

∂

KrFRMrFFM() ( )

OOC



, (10.2.12')

()

() ( ) () () ( ) ( ) ()

OOOOOOCO

∂τ

τ = =τ +τ =τ +τ +τ +τ

∂



HFRFFFR

(10.2.14')

dd d d d d d d

FR FR

TW W WW W=+=++=⋅+⋅FrRr

ddd

=⋅ + ⋅ +⋅FrF rRr, (10.2.15')

rr r r r

∂

==⋅+⋅=+⋅+⋅

∂



F v Rv F v Rv

, (10.2.16')

so that we can state corresponding theorems. In case of holonomic and scleronomic

constraints we have

dd0

W =⋅ =Rr

, hence 0

⋅

=Rv .

Starting from the above results, we can find, in certain conditions, first integrals and

may state conservation theorems with respect to a non-inertial frame of reference. Thus,

using the theorems of Chap. 6, Subsec. 1.2.5, we obtain, for a free particle:

Theorem 10.2.7 (conservation theorem of momentum). The momentum (and the

velocity) of a free particle with respect to a non-inertial frame of reference is conserved

in time if and only if the relative force which acts upon the particle in this frame (the

sum of the resultant of the given forces which act upon the particle and the

complementary forces) vanishes.

Theorem 10.2.8 (conservation theorem of moment of momentum). The moment of

momentum of a free particle with respect to the pole of a non-inertial frame of

reference is conserved in time if and only if the moment of the relative force which acts

upon it in this frame (the sum of the moment of the resultant of the given forces which

act upon the particle and the moment of the complementary forces), with respect to the

same pole, vanishes.

Theorem 10.2.9 (conservation theorem of torsor). The torsor of the momentum of a

free particle with respect to the pole of a non-inertial frame of reference is conserved in

MECHANICAL SYSTEMS, CLASSICAL MODELS

624

time if and only if the torsor of the relative force which acts upon it in this frame (the

sum of the resultant of the given forces which act upon the particle and the

complementary forces), with respect to the same pole, vanishes.

Theorem 10.2.10 (conservation theorem of the mechanical energy). The mechanical

energy of a free particle with respect to a non-inertial frame of reference is conserved

in time if and only if the sum of the given forces which act upon the particle and the

transportation force is conservative.

The conditions in the latter theorem (in which the mechanical energy contains also

an energy due to the transportation force) are not so easy to fulfil. If the resultant

the given forces is a conservative one, which derives from a simple or from a

generalized potential, then we can write

dd( ) d

ETV

+=⋅Fr. (10.2.17)

In particular, if

′

=a0

(hence const

′





) and const=





, hence if the

transportation motion is a finite motion of rototranslation of constant velocities of

translation and rotation (the movable frame has a motion of rotation with a constant

angular velocity around an axis which passes through its pole, that one having a

rectilinear and uniform motion with respect to the fixed frame), we can write

dd()d(,,d)(,,d)

mm m m⋅=− ⋅=− ××⋅=− × = ×Fr a r r r rr r r

ωωωωω

()(d)d()

⎡

⎤

=×⋅×= ×

⎣

⎦

rr rωω ω

we obtain thus a first integral (called, sometimes, the generalized first integral of the

energy, because it is reduced to the first integral of the energy if

) of the form

()

ETV h=+= × +rω , consth

. (10.2.17')

In case of a particle subjected to constraints we get results analogous to those in

Chap. 6, Subsec. 2.1.3. If the constraints are holonomic and scleronomic, then the

relations (10.2.17), (10.2.17') maintain their form.

2.1.4 Inertial frames of reference. Galileo-Newton group

Starting from the equation (10.2.2), (10.2.2'), we will search the movable frames

(specified by the acceleration

′

a of the pole of the frame and by its angular velocity

) for which a free particle P is moving after the law

aF, (10.2.18)

hence after the same law as in the case of the fixed (inertial) frame. We notice that, in

this case, the sum of the complementary forces must vanish; hence, we must have

[

]

() ()2

′

−+=− +×+××+×=



aa a r r v 0

ωω ω (10.2.19)

Other considerations on particle dynamics

625

for any point at which the particle may be (for any

r ) and for any relative velocity

of it.

We assume that, starting from the same position vector

r , the particle P can have

the relative velocity

′

in one case of motion and the relative velocity

′′

in another

case of motion. Imposing the condition (10.2.19) in both cases and subtracting a

relation from the other, we find

()

′

′′

−=vv 0

for any

′

v and

′′

; it results that

we must have

= 0ω (hence,



too). Returning to the above condition, it follows

that

′

=a0

From the latter condition we see that one passes from the fixed frame to the movable

one by a transformation of space co-ordinates (to which a time transformation may be

added) of the form (6.1.42''), which forms a group with seven parameters. The

condition

0 shows that the movable frame can have only a finite geometric

rotation of the form (6.1.43), concerning its relative position with respect to the fixed

frame, so that the most general transformation which corresponds to the passing from a

frame to another one, modelling the motion of a particle in the form (10.2.18), is given

by (6.1.44) and forms the Galileo-Newton group with ten parameters, studied in Chap.

6, Subsec. 1.2.3. One can thus apply the Theorem 6.1.6 (of relativity) of Galileo, the

movable frame being – in this case – an inertial frame too, with respect to which the law

of motion maintains its form (acting only the given force and, eventually, the constraint

one). If we write the relation of transformation (6.1.44) for two particles

and

then we have

′

=++αrrvr,

′

rrvr,

ttt

′

+ ,

the tensor

corresponding to a finite rotation of the movable frame; we obtain thus

21 21

()

′′

−= −

rr rr, wherefrom

[][][][ ]

21 21 21 21 21 21

()() ()() ()()

′′

− = − = −⋅ −= −⋅−αααααrr rr rr rr rr rr

[

]

21 21 21

()()()=−⋅−=−δ rr rr rr,

δ being Kronecker’s tensor. Hence, the distance between two particles remains

invariant in a transformation of the Galileo-Newton group; the forces which depend

only on distances (e.g., the forces of Newtonian attraction) have the same property of

invariance. In this case, taking into account the invariance of the acceleration, it results

that the mass of the particle is invariant too (constant, property iii) of the mass; see also

Chap. 1, Subsec. 1.1.6).

If, in a non-inertial system of reference, we determine experimentally the sum

+FF of the complementary forces, then one calculate the quantities

′

and ω

which specify the motion of the frame (neglecting a rectilinear and uniform motion of

translation, which cannot be put in evidence by mechanical experiments). As a matter

of fact, by no experiment of physical (not only mechanical) nature a preferential inertial

(e.g., “fixed”) frame cannot be put in evidence, all inertial systems being thus

equivalent.

MECHANICAL SYSTEMS, CLASSICAL MODELS

626

2.1.5 Principle of equivalence

Let us suppose that the particle P is subjected to the action of a uniform

gravitational field (the terrestrial gravitational field)

Fg and let us consider the

motion with respect to a non-inertial frame of reference in rectilinear and uniform

accelerated motion of translation (hence, for which

′

ag,

0 ); in this case,

m=−Fg and

=F0, so that

F0, the equation of motion (10.2.2') leading thus

=a0. We notice that an observer, situated in an elevator which is moving in the

direction of the gravitation and is acted upon by a force equal to

mg , cannot perceive

the gravitational field (particularly, if he could not be in contact with the universe of the

exterior of the elevator); it is the case of imponderability, considered in Subsec. 2.1.2.

The mass plays two different rôles in the identity

′

ag; in the left member is

put in evidence the aspect of inertial mass (which leads to the inertial transportation

force), while in the right member appears the aspect of gravity mass (called heavy mass

too) (see also Chap. 1, Subsecs 1.1.6 and 1.2.1). This observation led A. Einstein to

state the principle of equivalence between the gravity mass and the inertial one in the

general relativistic model of mechanics; thus, the two properties of the mass represent

two different aspects of the same material quantity. This result has been confirmed by

the experiments performed by Eötvös and Zeeman, by Southern and Zeeman etc.

2.1.6 Relative equilibrium

The location

=rr is called position of relative equilibrium of a free particle P

(which is in relative rest with respect to a non-inertial frame of reference) if the

equation of motion (10.2.2), (10.2.2') with the initial conditions

()t =rr,

()

t =v0 admits as solution

()t

rr,

∀

≥ ; in this case, we have ()

t =v0,

()t =a0,

∀

≥ . It results

F0, so that

+=FFF0, (10.2.20)

and we can state (the condition (10.2.20) is sufficient too, because

=F0 leads to

=v0, the rectilinear and uniform motion with respect to the movable frame being

thus excluded)

Theorem 10.2.11 (theorem of relative equilibrium). A free particle is in relative

equilibrium (with respect to a non-inertial frame of reference) if and only if the sum of

the resultant of the given forces which act upon that particle and the transportation

force vanishes.

′

=a0

, =



ω 0 (the non-inertial frame has a finite motion of rototranslation with

constant velocities of translation and rotation), then the transportation force

()

−××

ωFr (10.2.21)

is a centrifugal one.

Other considerations on particle dynamics

627

In case of a particle subjected to bilateral constraints, the necessary and sufficient

condition of relative equilibrium (with respect to a non-inertial frame of reference)

reads

=+ + =FRFFR0, (10.2.20')

where

R is the constraint force.

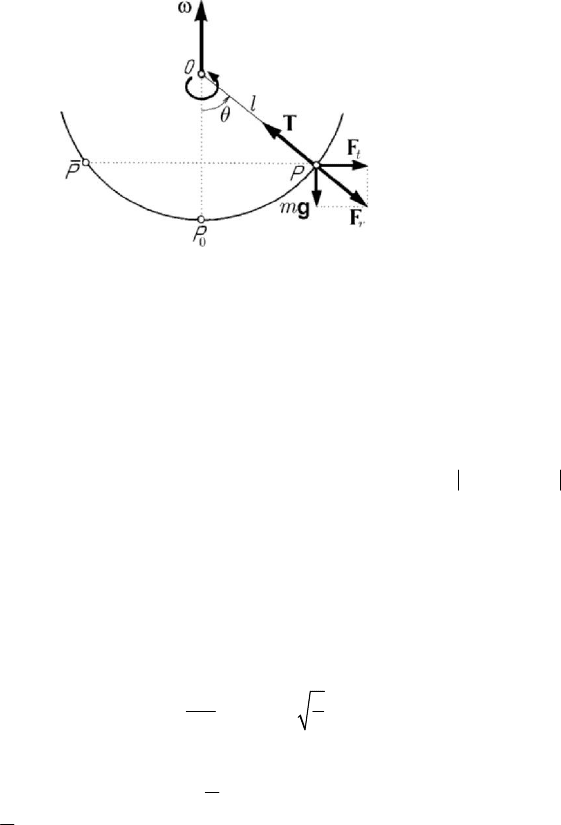
Figure 10.6. Heavy particle constrained to move on a circle in uniform rotation

about a vertical diameter of it.

Let us consider the case of a heavy particle

P of mass m , constrained to move on a

circle in uniform rotation about a vertical diameter of it, with the angular velocity

(along one of the axes of the inertial frame of pole

O ); for instance, let us suppose that

the particle

P is a small heavy sphere, situated at the end of a perfect inextensible

thread of length

l (Fig.10.6). We choose the non-inertial frame with the pole at O too,

the axis of which coincides with the rotation axis of the movable frame. The particle is

acted upon by the gravity force

mg , by the centrifugal force ()

××rωω

sinmlωθ= and by the constraint force T (the tension in the thread). Projecting the

equation of equilibrium (

+=gF T 0) on the normal to the force T and along

the direction of it, we get

cos sin

Fmgθθ

sin cos

TF mgθθ

The positions of relative equilibrium are given by

sin 0θ = ,

cos

= ,

ω∀> ; (10.2.22)

hence, excepting the point

P (which corresponds to 0θ

), we obtain two symmetric

positions of relative equilibrium

P and P . For

P it results the tension Tmg= ,

while for

P and P the tension is

Tmlω

Let be an ideal liquid in rest with respect to a vessel in uniform accelerated

translation with respect to an inertial frame of pole

′

; the non-inertial frame is linked

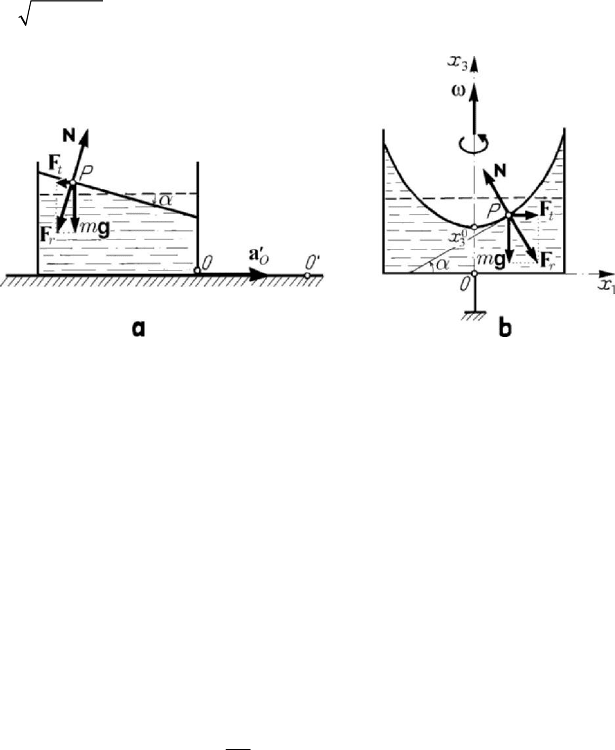
MECHANICAL SYSTEMS, CLASSICAL MODELS

628

to the vessel, the velocity of the pole

being

const

′





with respect to the pole O

′

=a0

, then the free surface of the liquid (in rest with respect to the fixed frame) is

a horizontal plane. A particle

, of mass m , of the free surface of the fluid

(Fig.10.7,a) is in equilibrium under the action of the gravity force

mg , of the

transportation force

′

=−Fa and of the constraint force N (normal to the

separation surface). If the liquid is in relative equilibrium with respect to the vessel in

motion of translation, then the free surface is a plane inclined with respect to the

horizontal one by an angle

α given by tan /

agα

′

, while the constraint force is

Nma g

′

=+.

Figure 10.7. Relative equilibrium of a liquid with respect to a vessel in uniform accelerated

translation (a) or in uniform motion of rotation about a vertical axis of symmetry (b).

If the vessel has a uniform motion of rotation about a vertical axis of symmetry,

linked to the fixed frame, the movable frame being connected to the vessel, then a

particle

, of mass m , of the separation surface of the fluid is acted upon by the

gravity force

mg , by the centrifugal force ()

−××

ωFr, of magnitude

Fmxω=

, and by the constraint force

N (Fig.10.7,b). Projecting the equation of

relative equilibrium (

m ++=gF N 0) on the tangent at P to the meridian curve of

the free surface, we get

cos sinmx mgωα α= ; observing that

tan d / dxxα = , it

results

31 1

d/d /xx xgω= , the meridian curve being a parabola of equation

(

)

220

313

/2xgxxω=+

. Hence, the free surface is an axial-symmetrical paraboloid of

equation

()

22 0

3123

xxxx

=++. (10.2.23)

As well, the constraint force is given by

/cosNmg α

Other considerations on particle dynamics

629

2.2 Elements of terrestrial mechanics

After a study of the influence of the transportation force (inclusive of the centrifugal

force) and of Coriolis’ force on the motion of a particle on Earth’s surface (using a

geocentric or a heliocentric frame), some phenomena due to non-inertial frames on the

Earth surface are considered. Thus, the phenomenon of tides is explained, the terrestrial

acceleration is calculated, the deviation of the plummet from the local vertical, the

deviation towards the east in free falling and Baer’s law are determined and the idea of

imponderability is explained; as well, Foucault’s pendulum, very important for the

knowledge of terrestrial motions, is presented. In particular, one obtains the case of

relative equilibrium.

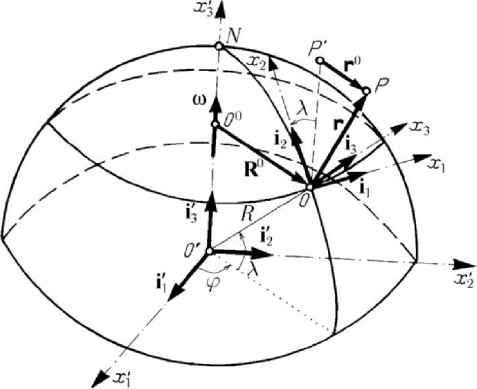
2.2.1 Geocentric and heliocentric frames

In the study of motion of a particle on the Earth surface, we considered till now that

the local frame of reference is inertial (absolute); we obtained thus the motion of the

particle with respect to this frame, where the motion of the Earth was not taken into

consideration (an approximation of the physical reality). Assuming that the Earth is

spherical, we choose the orthonormal frame with the pole at a point

O on the boreal

Figure 10.8. Motion of a particle with respect to a geocentric (inertial) frame of reference.

hemisphere; the

Ox -axis is tangent to the parallel of the point O , being directed

towards the east point, the

Ox -axis is tangent to the local meridian, being directed

towards the north, while the

Ox -axis is directed towards the ascendent local vertical

(the same direction as

′





, O

′

being the centre of the Earth (Fig.10.8). If a heavy

particle falls free from the height

h (sufficient great, without other influences) and if

we assume that the considered frame of reference is inertial, then the equations of the

rectilinear trajectory are

0xx

= ,

/2xhgt=− ; but, experimentally, it is seen

MECHANICAL SYSTEMS, CLASSICAL MODELS

630

that a deviation towards the east point, along the parallel (

≠

) takes place. This

deviation is, obviously, due to Earth’s motion of rotation (the local frame of reference is

non-inertial). The most simple frame which can be chosen as an inertial one is the

geocentric frame of reference (Ptolemy’s frame), assuming that the pole is at the centre

′

of the Earth; usually, the equatorial plane is taken as principal plane, the

′′

-axis

being directed towards the vernal equinoctial point (on the celestial sphere of radius

equal to unity, at the intersection of the equatorial plane with the ecliptic plane, which

contains the orbit of the Earth), while the

′

-axis is normal to that plane (hence, it is

the rotation axis of the Earth) (Fig.10.8). Practically, a system of stars considered

“fixed”, which allows to specify the axes of the considered frame, is used.

The local frame of reference is rigidly linked to the Earth, hence it has a motion of

rotation defined by the vector

, directed along the axis of the poles, from the south to

the north. We notice that a complete rotation of the Earth about its axis takes place in a

sidereal day, which is smaller than a mean solar day by

3 min 56 s; hence, a sidereal

day has

24 60 60 (3 60 56) 86164 s⋅⋅−⋅+ = (seconds of mean solar time), so that

the magnitude of the vector is given by

7.292 10 rad/ s

86164

−

=≅⋅ , (10.2.24)

the unit of time being the second. In the non-inertial frame of unit vectors

i ,

1, 2, 3j = , the rotation vector is given by

cos sinωλ ωλ

ii, (10.2.25)

where

λ ,

[

]

0, / 2λπ∈ in the boreal hemisphere and

[

]

/2,0λπ

∈

− in the austral

hemisphere, is the local latitude. The unit vectors of the axes of the two frames are

linked by the relations

112

sin cosϕϕ

′

−+iii,

2123

sin cos sin sin cosλϕ λϕ λ

′

′′

=− − +iiii

, (10.2.26)

3123

coscos cossin sinλϕ λϕ λ

′

′′

=++iiii

where

ϕ , [0,2 )ϕπ∈ , is the local longitude. Taking into account (A.2.36) and the fact

that the pole of the movable frame has a circular motion along the parallel of radius

cosR λ , where R is Earth’s radius, we get

0ω = ,

cosωϕλ

 ,

sinωϕλ

 ; (10.2.25')

observing that

ωϕ=  , the formulae (10.2.25') correspond to the expression (10.2.25)

previously obtained for the rotation vector, what was to be expected, taking into

account the results in Chap. 5, Subsec. 2.2.2.

Other considerations on particle dynamics

631

But there are some phenomena for which the use of a geocentric frame of reference

leads to results which are not in concordance with the physical reality; in this case, one

must choose another frame as inertial one, i.e. a heliocentric frame (Copernicus’ frame),

with the pole

′′

at the centre of mass of the Sun (very close to the centre of mass of

the solar system, which – as it will be shown in Chap. 11, Subsec. 1.2.5 – has a

rectilinear and uniform motion). The heliocentric frame may be ecliptic or equatorial, as

it has been shown in Chap. 1, Subsec. 1.1.4, its axes

′

′′′

′

′′′

′′ ′′

being

specified correspondingly. The geocentric frame previously considered is, in this case, a

non-inertial one, its axes having fixed directions (the corresponding rotation vector

′

is equal to zero); indeed, corresponding to Kepler’s first law, the Earth has also a

motion of revolution which is – in fact – a motion of translation.

If neither the heliocentric frame of reference cannot be considered to be inertial, then

one can choose a galactocentric frame a.s.o.

2.2.2 Motion of a particle at the Earth surface. Relative equilibrium

Let us consider, first of all, the case of a heliocentric frame (an inertial frame), the

geocentric one being non-inertial. The equation of motion (10.2.2') with respect to the

latter frame of reference is written in the form (neglecting the effect of the centrifugal

force due to the motion of revolution of the Earth; Coriolis’ force vanishes, because the

motion is plane)

′

′′′

−aF a, (10.2.27)

where

′

′′ ′′ ′





, while

′

F is the force which acts upon the particle

of mass m .

Let (

is, in fact, an acceleration)

()

mQ f CQ

=−





(10.2.28)

be the force of universal attraction by which a celestial body

C of centre C and mass

acts upon a particle Q of mass

. With respect to the heliocentric frame, the

equation of motion of an element of mass

d()d

mQVμ

of the Earth, situated at

the point of position vector

r , reads

() d () ()d

QV QQVμμ

′′

∑

where we have put into evidence the action of the celestial bodies

, 1,2,...j = ,

upon that element; but (

V is the volume of the Earth)

()

() d () d

QQEQEQ

QV QV m m

μμ

′′ ′′ ′′ ′′

===

∫∫

arra,

where we took into account the formula (3.1.3), which gives the position of the centre

of mass

′

of the Earth, so that we get

MECHANICAL SYSTEMS, CLASSICAL MODELS

632

() ()d

mQQVμ

′

′′

∑

∫

()d

mQVμ=

∫

Finally, the equation of motion (10.2.27) becomes

[

]

() () ()

EM P

mmPPmP

′

=+ + +

∑

aF f f f

() () () ()d

SM P

QQ Q QV

⎡⎤

−++

⎢⎥

⎣⎦

∑

∫

ff f , (10.2.29)

where

F is the resultant of the other forces which act upon the particle P (forces of

resistance of the medium, forces of friction, forces of electromagnetic nature etc.) and

where we have put into evidence the action of the Sun, of the Moon and of the other

planets

P ,

1,2,...j =

. Neglecting the action of the planets in comparison with the

action of the Sun and of the Moon, because of the great distances from these planets to

the Earth, and applying a mean value theorem, we can write, with a good

approximation,

[]

() () ()d

ESM

mOOQVμ

′

′′ ′ ′

∫

af f ,

so that

() ()

SM M

OOfOOfOO

OO O O

′

′′ ′ ′ ′′ ′ ′

=+ =− −

′′ ′ ′



 

af f , (10.2.28')

where

O is the centre of the Moon. The equations (10.2.29) become

[

]

[

]

() () ( ) () ( )

ESS MM

mmPmPOmPO

′′′

++ −+ −aF f f f f f . (10.2.29')

Observing that

()

′

′′

()

′

we may write

(

)

()

6.040 10

()

−

′

=≅⋅

′′ ′

()

3.379 10

()

−

′

⎛⎞

=≅⋅

⎜⎟

′

⎝⎠

where we took into account the relations

3.330 10

mm=⋅ , 81.301

mm≅ ,

2.348 10OO R

′′ ′

≅⋅, 60.336

OO R

′

≅ (in fact, the distance OO

′′ ′

put into