Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics
Подождите немного. Документ загружается.

Other considerations on particle dynamics
633
evidence is the distance from the centre
O
′
′
of the Sun to the centre of mass of the
mechanical system formed by the Earth and the Moon; but this latter centre is inside the
terrestrial surface, at approximative
/2ROO
′
′′
from the centre O
′
, so that it may
be identified, with a good approximation, with
O
′
). Hence, the influence of the forces
of attraction of the Sun and of the Moon can be neglected with respect to the force of
attraction of the Earth. Let us consider the forces
()
S
Pf and ()
M
Pf too. We will have
1
min
() ( )
SS
PP=ff
,
2
max
() ( )
SS
PP
=
ff
(Fig.10.9), as well as
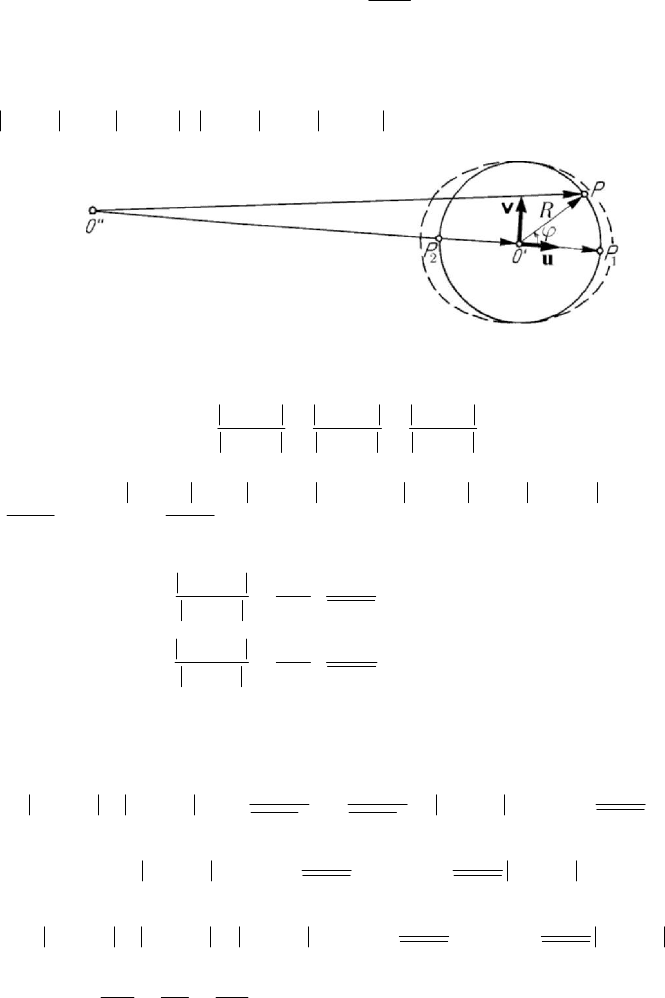
Figure 10.9. The influence of the forces of attraction of the Sun and of the Moon
with respect to the force of attraction of the Earth.
12
() () ()
() () ()
SSS
EEE
PPO
PPP
′
≅≅
fff
fff
;
analogously,
1
min
() ( )
MM
PP
=
ff and
2
max
() ( )
MM
PP
=
ff, so that
(
1
61.336
M
OP R≅
,
2
59.336
M
OP R≅
)
2
1
6
1
()
3.269 10
()
M
M
EE
M
P
m
R
Pm
OP
−
⎛⎞
=≅⋅
⎜⎟
⎝⎠
f
f
,
2
2
6
2
()
3.494 10
()
M
M
EE
M
P
m
R
Pm
OP
−
⎛⎞
=≅⋅
⎜⎟
⎝⎠
f
f
.
In fact, we are interested in the differences (components along
1
versOP
′
=
u )
1
22
1
() ()
MM
MM
M
M
mm
POf f
OP
OO
′
−+ =−+
′
ff
2
()1 1
M
M
R
O
OO
−
⎡
⎤
⎛⎞
′
=−+
⎢
⎥
⎜⎟
′
⎝⎠
⎢
⎥
⎣
⎦
f
()1 1 ... 2 ()
MM
MM
RR
OO
OO OO
⎡⎛ ⎞⎤
′′
≅−−+≅
⎜⎟
⎢⎥
′′
⎣⎝ ⎠⎦
ff
2
2
() () ()1 1
MMM
M
R
POO
OO
−
⎡
⎤
⎛⎞
′′
−+ = −−
⎢
⎥
⎜⎟
′
⎝⎠
⎢
⎥
⎣
⎦
fff
2()
M
M
R
O
OO
′
≅−
′
f
;
in this case (
21
OP OP OP≤≤)
MECHANICAL SYSTEMS, CLASSICAL MODELS
634
3
7
() ( )
2 1.120 10
()
MM
M
EE
M
PO
m
R
Pm
OO
−
′
−
⎛⎞
≤≅⋅
⎜⎟
′
⎝⎠
ff
f
.
Analogously, we get
(
)
3
8
() ( )
2 5.145 10
()
SS
S
EE
PO
m
R
Pm
OO
−
′
−
≤≅⋅
′′ ′
ff
f
.
In conclusion, to study phenomena connected to an isolated particle, situated on the
Earth surface, we can use – with a very good approximation – the equation
()
r
E
mmP
′
=
+aF f , (10.2.29'')
written with respect to a geocentric frame of reference, which is non-inertial.
Equating to zero the relative motion, we obtain the condition of relative equilibrium
(with respect to the Earth) in the form
()
E
mP
+
=Ff 0. (10.2.30)
Figure 10.10. Relative equilibrium of a particle with respect to the Earth.
Let be a movable frame of reference
123
Ox x x (non-inertial), rigidly linked to the
Earth, so that
OO
′
≡ and
33
Ox O x
′
′
≡ , its position being specified by the angle
θ
(Fig.10.10); we may write the equations of motion with respect to the new frame in the
form
() ( ) 2
r r
E
mmPmm m=+ −×−××− ×
ω
ωω ωaF f r r v, (10.2.31)
where ω is the rotation vector (
ωθ
=
), while OP
=
r . We notice that
3
ω
′
=ω i ,
where
ω is given by (10.2.24); using Rivals’ formula (5.2.6''') and neglecting
ω (the
angular velocity ω is, with a good approximation, constant, the variation in time of the
poles’ axis being negligible), we may write

Other considerations on particle dynamics
635
20
() 2
rr
E
mmPmmω=+ + − ×ωaF f r v, (10.2.31')
where
0
PP
′
=
r (Fig.10.10). The condition of relative equilibrium (with respect to the
movable frame) is given by
20
()
E
mPmω
+
+=Ff r0. (10.2.32)
If we choose the movable frame rigidly linked to the Earth, with the pole at a point
O on the Earth surface (Fig.10.8) (because the particle is in motion in the vicinity of
this pole), the equation of motion with respect to a local frame (non-inertial) becomes
20
() ( ) 2
r r
E
mmPm mω=+ + −× × − ×
⎡⎤
⎣⎦
ωω ωaF f R r v; (10.2.33)
we notice that the acceleration
O
′
a with respect to the frame
123
Ox x x
′
′′′
, considered to be
fixed, is given by
20
O
ω
′
=−
aR
, with
00
OO
=
R (the pole O has a uniform motion
along a parallel of the Earth, of radius
0
R
). In components, we may write (we assume
that the force
()
E
Pf is applied in the vicinity of the pole
O
, along the descendent
vertical of that pole, the gravitational field being uniform)
2
11 3 2 1
2(cos sin)mx F m x x m xωλ λω=− − + ,
[
]
2
22 1 3 2
2 sin sin ( )cos sinmx F m x m x R xωλωλ λ λ=− − + − , (10.2.33')
33 1
() 2 cos
E
mx F m P m xωλ
=
−+ f
[
]
2
32
cos ( )cos sinmxRxωλ λ λ++−.
In general, this system of equations cannot be exactly integrated; we must use
approximate methods of calculation, e.g. the method of the small parameter (after
Poincaré), developing the solution in a power series after that parameter (from (10.2.24)
it results that
Tεω= , where T is a time specific to the considered mechanical
phenomenon,
ε being a non-dimensional small parameter)
2
0
12
...εε
=
++ +rr r r . (10.2.34)
If we replace in (10.2.33') and identify the powers of the same order as
ε , we can write
successively
(0)
1
1
mx F= ,
(0)
2
2
mx F= ,
(0)
3
3
()
E
mx F m P=− f , (10.2.35)
(
)
(1) (0) (0)
13 2
2cos sinxx xλλ=− − ,
(1) (0)
21
2sinxxλ=− ,
(1) (0)
31
2cosxxλ= ,…
(10.2.35')
The approximation of nth order is obtained by quadratures, starting from the
approximation of (n-1)th order; obviously, the convergence of the solution must be also
verified. The approximation of order zero (10.2.35) corresponds to the neglect of the

MECHANICAL SYSTEMS, CLASSICAL MODELS
636
motion of rotation of the Earth. For instance, in case of initial conditions of the form
0
(0) =rr,
0
(0) =vv, we have
0
0
(0)
=
rr,
0
0
(0) =vv, (10.2.36)
1
(0)
=
r0,
1
(0)
=
v0,… (10.2.36')
a.s.o. If the initial conditions depend on
ω , then one uses systematically expansions in
power series with respect to the small parameter
ε and to each approximation are put
initial conditions which multiply the same power of
ε .
The condition of relative equilibrium with respect to the local frame
123
Ox x x is
written in the form
20
() ( )
E
mP mω++ −××=
⎡⎤
⎣⎦
Ff R r 0ωω . (10.2.37)
We put in evidence, in what follows, the influence of each term which appears in this
equation.
2.2.3 Acceleration of the centre of the Earth. Tide
The translation acceleration
O
′
′
′
a
of the centre O
′
of the Earth with respect to the
heliocentric frame
123
Oxxx
′′ ′′ ′′ ′′
is due, as we have seen, to the forces of attraction of the
Sun, of the Moon and of other planets (the latter ones may be neglected because of the
great distances from those planets to the Earth). The magnitude
O
a
′
′
′
of the acceleration
(due to the Sun and to the Moon) is given by
() ( )
OO O
aaSaM
′′ ′
′
′′′ ′′
=
+ , where
2
()
S
O
m
aS f
OO
′
′′
=
′′ ′
,
2
2
() ()
MM
OO
S
M
M
mm
OO
aM f aS
m
OO
OO
′′
′′ ′
⎛⎞
′′ ′′
==
⎜⎟
′
′
⎝⎠
;
taking
83 2
6.673 10 cm / g s
f
−
=
⋅⋅,
33
1.989 10 g
S
m =⋅ ,
25
7.347 10 g
M
m =⋅ ,
13
1.496 10 cmOO
′′ ′
=⋅
,
10
3.844 10 cm
M
OO
′
=⋅
, we obtain
()
O
aS
′
′
′
1
5.931 10
−
=⋅
2
cm/s (which leads to a force of 0.5931 dyne per 1 g mass) and ()
O
aM
′
′′
2
0.00559 ( ) 0.0033 cm/s
O
aS
′
′′
== (corresponding
0.0033 dyne per 1 g mass).
For a better approximation of the influence of that acceleration, let us return to the
equation (10.2.29'); we evaluate thus the magnitude of the force
[]
33
() ( )
SS
SS
mm mm
mP O f OPf OO
OP OO
′
′′ ′′ ′
−=− +
′′ ′′ ′
ff . (10.2.38)
Assuming that the Sun is at an infinite distance, hence that
OP OO
′′ ′′ ′
, the
component of this force along the unit vector
versOO
′
′′
=
u (Fig.10.9) is given by
Other considerations on particle dynamics
637
[]
()
22
() ( )
cos
SS
SS
u
mm mm
mP O f f
OO R OO
ϕ
′
−=− +
′
′′ ′′′
+
ff
(
)
2
2
11 cos
S
mm
R
f
OO
OO
ϕ
−
⎡⎤
=−+
⎢⎥
′′ ′
⎣⎦
′′ ′
(
)
2
112 cos ...
S
mm
R
f
OO
OO
ϕ
⎡
⎤
=−− +
⎢
⎥
⎣
⎦
′′ ′
′′ ′
,
wherefrom
[]
3
() ( ) 2 cos 2 ( ) cos
S
SS S
u
mm
R
mP O f R mO
OO
OO
ϕϕ
′′
−≅ =
′′ ′
′′ ′
ff f
, (10.2.39)
with
(
)
1
,OP OPϕ
′′
=
. But OP OO OP
′
′′′′′
=
+
, so that the force (10.2.38) reads
[]
33 3
11 1
() ( )
SS S
mP O fmm OO OP
OO OP OP
⎡
⎛⎞ ⎤
′′′′′
−= − −
⎜⎟
⎢
⎥
⎣
⎝⎠ ⎦
′′ ′ ′′ ′′
ff ;
but
22
2
2cosOP OO R OOR ϕ
′′ ′′ ′ ′′ ′
=++
, so that
(
)
3 3/2
2
12 cos
OO R R
OP OO OO
ϕ
−
′′ ′
⎛⎞
⎡⎤
=+ +
⎜⎟
⎢⎥
′′ ′′ ′ ′′ ′
⎣⎦
⎝⎠
()
(
)
2
2
3
1 3 cos 5 cos 1 ...
2
RR
OO OO
ϕϕ=− + − +
′′ ′ ′′ ′
.
Projecting on the unit vector
u
and neglecting the terms in
(
)
2
/ROO
′
′′
with respect to
/ROO
′′ ′
, we find again the component (10.2.39); the projection on the unit vector v
(normal to
u , Fig.10.9) is given by
[]
3
() ( ) sin ( ) sin
S
SS S
v
mm
R
mP O f R mO
OO
OO
ϕϕ
′′
−≅ =−
′′ ′
′′ ′
ff f
, (10.2.39')
the corresponding component being directed towards the diameter
21
PP .
Hence, the particle
P is acted upon, besides the gravity force ()
E
mPf , by a force
due to the attraction of the Sun. We have seen, at the preceding subsection, that this
force can be neglected; but, in case of a continuous mechanical system of great
dimensions, the contribution of the terms due to this force of attraction is added and
becomes noticeable, so that it must be taken into consideration. If such a mechanical
system is rigidly connected to the Earth, e.g. its solid crust, then the effect of the force
of attraction is not observed, but if this system is not rigidly linked to the Earth (the case
of seas and oceans or of fluid masses in the interior of the terrestrial sphere), then
appears the phenomenon called tide. The component along
u has extreme values for
0ϕ = (the face opposite to the Sun, for which the water is repulsed) and for ϕπ=
(the face towards the Sun, when the water is attracted) and we have (Fig.10.9)

MECHANICAL SYSTEMS, CLASSICAL MODELS
638
[]
extr
() ( ) 2 ( )
SS S
u
R
mP O mO
OO
′′
−≅±
′
′′
ff f
, (10.2.40)
the component along
v
vanishing in this case. The component along
u
is equal to zero
for
/2ϕπ=± , while the component along v has extreme values
[]
extr
() ( ) ( )
SS S
v
R
mP O mO
OO
′′
−≅
′
′′
∓ff f . (10.2.40')
In this zone, the particles of fluid are attracted by a greater force towards the Earth. At a
point on the Earth surface, the force of attraction is varying in time, because the angle
ϕ varies together with the rotation of the Earth. The extreme values of the magnitude
of this force (hence, the phenomenon of tide, the flood and the ebb, respectively) appear
twice in 24 hours (once when the Sun passes at the local meridian and once when it
passes at the opposite one). It is obvious that the level of the tides is greater at the
equatorial zone and tends to zero near the polar circle.
One can study the influence of the Moon too, obtaining analogous formulae; thus
[]
extr
() ( ) 2 ( )
MM M
u
M
R
mP O mO
OO
′′
−≅±
′
ff f , (10.2.41)
[]
extr
() ( ) ( )
MM M
v
M
R
mP O mO
OO
′′
−≅
′
∓ff f
. (10.2.41')
Introducing the numerical data mentioned above, we notice that
[
]
[]
[
]
[]
extr extr
extr extr
() () () ()
() () () ()
MM MM
uv
SS SS
uv
mP O mP O
mP O mP O
′
′
−
−
=
′′
−−
ff ff
ff ff
3
()
2.177
()
M
M
SS
MM
O
m
OO OO
Om
OO OO
′
′′ ′ ′′ ′
⎛⎞
===
⎜⎟
′
′′
⎝⎠
f
f
;
it results that the effect of the attraction force of the Moon on the tides is approximative
twice greater than that of the Sun, although the mass of the Moon is smaller than that of
the Sun, because it is closer to the Earth than the Sun.
2.2.4 State of imponderability
Let us consider the translation motion of a spatial vehicle, the mass centre
O
of
which describes an ellipse around the Earth. With respect to a non-inertial frame of
reference with the pole at
O
, we can write the equation of motion of a particle
P
of
mass
m , situated in the vehicle, in the form
[]
33
() ()
EE
r
EE
mm
mmPOmfOPfOO
OP OO
⎡
⎤
′
′
=+ − =+ − +
⎢
⎥
⎣
⎦
′′
aF f f F , (10.2.42)
Other considerations on particle dynamics
639
where
O
′
is the centre of mass of the Earth, the chosen fixed geocentric frame being
considered inertial; we have neglected the force of attraction of the spatial vehicle, as
well as the attraction forces of the Sun, of the Moon and of other planets, the equation
(10.2.42) being similar to the equation (10.2.28').
Observing that
OP OO OP
′′
=+
, we may also write
33 3
11 1
r
E
mfmm OOOP
OO OP OP
⎡
⎛⎞ ⎤
′
=+ − −
⎜⎟
⎢
⎥
⎣
⎝⎠ ⎦
′′ ′
aF
.
If
(
)
,OOOPϕ
′
=
, then we have
1/2
2
12 cos 1 cos ...
O P OP OP OP
OO OO OO OO
ϕϕ
⎡⎤
′
⎛⎞
=+ + =+ +
⎢⎥
⎜⎟
′′′ ′
⎝⎠
⎣⎦
,
so that
OP OO
′
′
≅
; on the other hand OP O P
′
. The equation of motion is thus
reduced to
r
m =aF. Assuming that the particle P is not in contact with the walls of
the cabin and that upon it there are not acting resistent forces of the medium, of an
electromagnetic or of another nature, due to certain facilities existing in the vehicle, it
results that
=F0, hence
r
=
a0 too; thus, the state of imponderability in the interior
of the spatial vehicle may be justified.
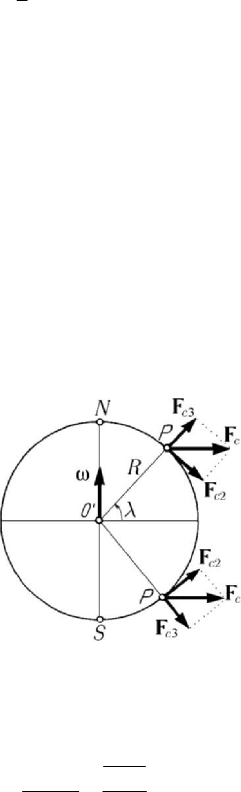
2.2.5 Centrifugal force
We have seen that the transportation force, in a motion with respect to the geocentric
frame of reference, contains – besides the force due to the acceleration of the Earth
centre and the force due to the angular acceleration vector
ω
, which can be neglected,
as we have mentioned before – also the centrifugal force (corresponding to the
centripetal acceleration)
20
()
c
mm=− × × =Frrωω ω
, (10.2.43)
in conformity to the results in Subsec. 2.2.2; this force is normal to the rotation vector
ω
, having the direction towards the exterior of the Earth. But, for particles at the Earth
surface, it is more convenient to use a local frame
123
Ox x x (Fig.10.8), so that we
obtain the centrifugal force
20
()
c
m ω=−××
⎡
⎤
⎣
⎦
FR rωω
, (10.2.44)
of components
2
11
c
Fmxω=
,
[
]
2
232
sin ( ) cos sin
c
Fm xR xωλ λ λ=− + − , (10.2.44')
[
]
2
332
cos ( )cos sin
c
Fm xR xωλ λ λ=+−.
MECHANICAL SYSTEMS, CLASSICAL MODELS
640
For the sake of simplicity, we assume that the particle is situated at the origin of the
local frame (
PO≡ ); it results (
2
cos
c
FmRωλ=
)
1
0
c
F = ,
2
2
1
sin 2
2
c
FmRωλ=− ,
22
3
cos
c
FmRωλ= , (10.2.44'')
where
λ is the local latitude (Fig.10.11).
As it can be noticed, the vector component
2c
F
(which vanishes at the equator and at
the poles, having an extreme value of
1.693
dyne per 1 g mass at the latitude of
45°
,
both in the boreal and in the austral hemispheres) is tangent to the meridian circle, being
directed towards the south in the boreal hemisphere and towards the north in the austral
one; hence, at any point on the Earth surface, this component has the tendency to
deviate the vertical direction (of the plummet) towards the equator. The vector
component
3c
F (which vanishes at the poles and has, at the equator, a maximal value of
3.386 dyne per 1 g mass, which represents 3.386/ 980.6 0.003453
≅
, hence
approximate
0.35%
from the weight of a mass of 1 g ) is along the local vertical
(along the radius of the Earth, considered to be spherical), being directed towards the
exterior of the Earth; this component has the tendency to decrease the effect of
attraction exerted by the Earth upon the considered particle.
Figure 10.11. Action of the centrifugal force on the Earth surface.
The ratio of the centrifugal force due to the motion of revolution of the Earth to the
centrifugal force due to its motion of rotation is given approximately by
(
)
2
1
0.176
365.25
OO
R
′′ ′
≅
;
the equation (10.2.27) and then the equation (10.2.33) are thus justified.
2.2.6 Deviation of the plummet from the local vertical
For a systematic study of the influence of the centrifugal force at the Earth surface,
we consider a particle
P , hanged up by a thread at the fixed point
Q
, rigidly connected
to the Earth (a plummet). The particle
P of gravity mass
g
m is acted upon by the
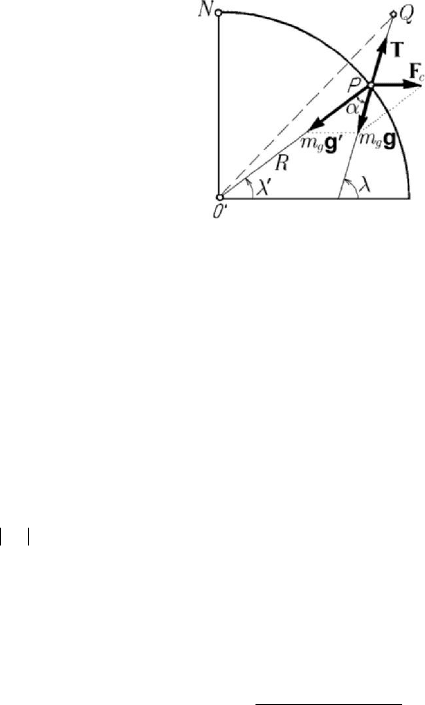
Other considerations on particle dynamics
641
terrestrial force of attraction
()
gg
E
mPm
′
=
fg, where
′
g is the gravity acceleration
(the theoretical acceleration) and by the tension
T in the thread. If the Earth would be
immovable, perfect spheric and with a distribution of mass with spherical symmetry,
then the particle
P would be on the line QO
′
, and the theoretical acceleration would
be the practical one (which is determined experimentally); but, due to the rotation of
the Earth, appears the centrifugal force
c
F too, so that the equation of relative
equilibrium (10.2.37) reads
gc
m
′
+
+=gTF 0. (10.2.45)
Figure 10.12. Deviation of the plummet from the local vertical.
Denoting
gcg
mm
′
+=gF g, where g is the terrestrial acceleration (the practical
acceleration), we obtain (Fig.10.12)
g
m
+
=gT 0
. (10.2.45')
The theoretical vertical
PO
′
is thus replaced by the practical vertical
QP
(the local
latitude being thus the astronomical latitude
λ , instead of the geographical latitude
λ
′
). In fact, a deviation of angle α (the angle between the theoretical vertical and the
practical one) of the plumb line is put into evidence.
Projecting the relation (10.2.45) on a direction normal to the practical vertical, we
get (
2
cos
c
i
mRωλ
′
=
F
, where
i
m is the inertial mass)
2
sin cos sin( ) 0
g
i
mg mRαωλλα
′′′
−+ +=
,
wherefrom (
/
g
i
kmm= )
2
22
sin cos
tan
cos
kR
gkR
ωλλ
α
ωλ
′
′
=
′
′
−
. (10.2.46)
The denominator of this expression is always positive, because the term
22
coskRωλ
′
22
3.386 cos cm/sk λ
′
=
is, in any case, less than
2
981 cm/sgg
′
≅≅
; hence,
tan 0α ≷ , so that 0α ≷ , as 0/2λπ
′
<
< or /2 0πλ
′
−
<<. In conclusion, the
MECHANICAL SYSTEMS, CLASSICAL MODELS
642
plummet is deviated from the theoretical local vertical towards the equator, as it was
shown in the preceding subsection. Differentiating the function (10.2.46), one can show
that
max
α is obtained for
2
2
cos 2
2
kR
gkR
ω
λ
ω
′
=
′
−
.
Taking into account the numerical data mentioned above, it results, with a very good
approximation,
cos 2 0λ
′
≅
, hence 45λ
′
≅
° ; in this case
2
max max
2
(tan )
2
kR
gkR
ω
αα
ω
≅≅
′
−
. (10.2.47)
If we notice that
(
)
222 2
cos 2gkR gkRωλ ω
′′′
−
, then we can also write
2
2
cos 1 cos
R
k
g
ω
αλ
′
≅−
′
,
2
sin sin 2
2
R
k
g
ω
αλ
′
≅
′
, (10.2.46')
the signs which are chosen corresponding to both hemispheres; the second of those
formulae played a particularly important rôle in the theory of mechanical systems, being
used to state experimentally the equality between the gravitational mass and the inertial
one. To this scope, Eötvös and Zeeman used a balance of torsion (Eötvös’s balance),
stating that, at any point of the Earth surface (and for all points having the same
latitude), one obtains the same angle
α for particles of different masses (an
approximation of
8
10
−
with respect to unity). On the basis of the mentioned formula, it
results
constk
=
. Hence, the gravity mass differs from the inertial one by a constant
factor
k , which can be taken equal to unity ( 1k
=
). Recent experiments of Dicke have
put in evidence this result with an approximation of
10
10
−
with respect to unity. As
well, they have been extended to the intimate structure of the atom.
If we take
1k =
in (10.2.47) and put
2
980.6 cm/sgg
′
≅≅ , we find
max
0.001730 radα ≅ or
max
556.92α
′
′′
≅
, hence the deviation of the plummet with
respect to the local theoretical vertical is at the most of six minutes, so that it can be
neglected.
2.2.7 Calculation of the terrestrial acceleration
From (10.2.45) and (10.2.45'), it results (we take 1k
=
)
2
cos vers
c
Rωλ
′′
=+
gg
F
, (10.2.48)
so that
22 22 242
2cos cosgg gR Rωλωλ
′
′′ ′
=− +
. (10.2.48')
Developing into series, we may write
