Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics
Подождите немного. Документ загружается.


Other considerations on particle dynamics
603
()
10
() ( )
i
m
n
ij
j
i
ij
f
xcxxδ
==
=−
∑∑
, (10.1.16'')
where
i
j
c
and
i
m are constants, while δ is Dirac’s distribution.
Taking into account the Theorem 10.1.2, we obtain the complementary constraint
force in the form
()
110
()
i
m
nn
j
c
ic ij i
iij
ttδ
===
== −
∑∑∑
RR β ; (10.1.17)
adding the solution corresponding to usual functions, it results the generalized
constraint force
()
110
() () ( )
i
m
nn
j
iiji
i
iij
ttf ttλδ
===
=+ −
∑∑∑
R ∇β . (10.1.17')
We may thus state (the result remains valid also in the case of two constraints)
Theorem 10.1.4 (theorem of the generalized constraint force). The generalized
constraint force which acts upon a particle subjected to holonomic and rheonomic
bilateral constraints is equal to the sum of the constraint force in the usual sense at the
moments in which that one is defined and the complementary constraint force due to the
moments of discontinuity and expressed by means of Dirac’s distribution and of its
derivatives.
This result shows that the operator
∇
, applied in the sense of the theory of
distributions, leads to a formula of the form
()
10
()
i
m
n
j
ij i
ij
f
fttδ
==
=+ −
∑∑
∇∇ β , (10.1.18)
where
123
(, , ;)
f
xxxt is a function of class
1
C , excepting the points of discontinuity of
the first species
i
tt= ,
1,2,...,in=
, and the symbol
∇
represents the operator ∇ in
the usual sense.
We notice that the number
i
m is indeterminate in the formulae (10.1.17), (10.1.17');
we make the same remark concerning the vectors
ij
β
. The significance of those
quantities is clear if we take into consideration the motion of the particle. Thus,
comparing the equation (10.1.14), (10.1.17') with the equation (10.1.9), we see that
1
1m = , while
0
10
m= vβ ,
0
11
m
=
r
β
; there are not other moments of discontinuity
unlike the initial moment.
We must also notice that, in order to ensure the existence and the uniqueness of the
solution, it is necessary to put supplementary conditions at the points of discontinuity.
Thus, returning to the example in Subsec. 1.1.1, (Fig.10.1), it is necessary to give,
besides the initial conditions at the point
A (at the moment 0t
=
), the velocity to the
MECHANICAL SYSTEMS, CLASSICAL MODELS
604
right of the point
B ; otherwise, the motion on the line segment BC remains
indeterminate. In conformity with the Cauchy-Lipschitz theorem, the force which acts
upon the particle must be of class
0
C ; just this condition is not satisfied at the point B .
To determine the motion on
BC , the initial conditions at B must be given (at the
moment
0
tt
=
); hence, one has to specify
0
(0)vt
+
(the direction of the velocity is
known). As we have seen, a relation of experimental nature between
0
(0)t −v and
0
(0)t +v is usually given.
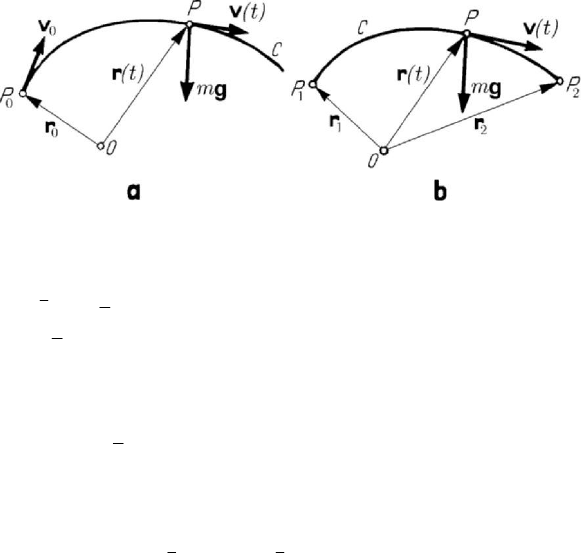
1.1.5 Motion of a heavy particle in vacuum. Bilocal problems
Let us consider the motion of a heavy particle in vacuum, acted upon by the force
m=Fg
, where
g
is the gravity acceleration. The corresponding Cauchy problem
consists in the determination of the position vector
()t
=
rr if the position vector
0
r
and the velocity
0
v at the initial moment
0
t
are given (see Chap. 7, Subsec. 1.2.1 too)
(Fig.10.3,a). We are in the case
const
=
F , so that the formula (10.1.12) allows to
write
Figure 10.3. Motion of a heavy particle in vacuum. Cauchy’s problem (a);
bilocal problem (b).
2
00000
1
()()() ()
2
ttt tt ttθ
++
=− +− +−r
g
vr
,
00000
()() () ()ttt tt ttθδ=− + − + −
+
v
g
vr
(10.1.19)
or
2
0000
1
()()()
2
ttt tt=− +− +r
g
vr, 0t ≥ . (10.1.19')
This result can be used to solve bilocal problems too; thus, if we have to determine
the motion of a heavy particle in vacuum, for which the conditions (Fig.10.3,b)
11
()t
=
rr,
22
()t
=
rr (10.1.20)
are fulfilled, then we may use as well a formula of the form (10.1.19), assuming that the
velocity at the initial moment
1
tt
=
is known. It results
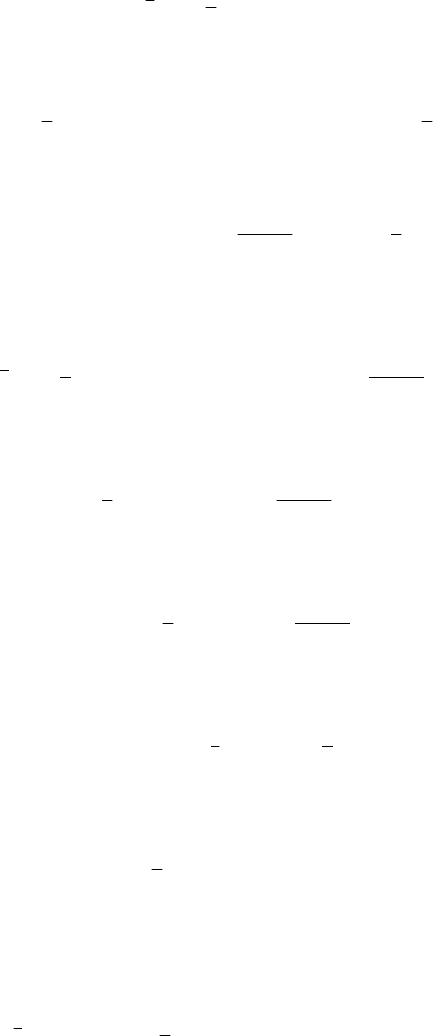
Other considerations on particle dynamics
605
2
11111
1
()()() ()
2
ttt tt ttθ
+
=− +− +−
+
r
g
vr.
If we put also the second condition (10.1.20), then we can write
2
221 211211
1
()() ()
2
tt tt ttθ
+
=− +− +−
+
r
g
vr
2
21 2111
1
()()
2
tt tt
=
−+−+
g
vr,
wherefrom
12121
21
11
()()
2
tt
tt
=−−−
−
vrr g;
we get thus the solution of the bilocal problem in the form
[]
1121 121 11
21
11
()()()( ) ()( )()
2
ttttttt tt tt
tt
θ
+
=− − −− + − −+−
−
++
rgrrr
(10.1.21)
or
[]
12 12 2 1
21
11
() ()() ()()
2
ttttt tttt
tt
=− − − + − + −
−
rgrr,
[
]
12
,ttt∈ .
(10.1.21')
The velocity is given by
12 21
21
11
() ( ) ( )
2
tttt
tt
⎡⎤
=− + + −
⎢⎥
−
⎣⎦
vgrr,
[
]
12
,ttt
∈
. (10.1.21'')
Let us consider also the case of the mixed bilocal problem for which the boundary
conditions
11
()t
=
rr,
22
()t
=
vv (10.1.22)
are put. If the velocity at the initial moment
1
tt
=
would be known too, then we could
write
11111
()() () ()ttt tt ttθδ=− + − + −
+
vgvr;
if we put now the second bilocal condition (10.1.22), then it results
221 1
()tt=− +vgv, wherefrom
1221
()tt
=
−−vv g. The trajectory of the particle
is thus given by the relation
1121 1211
1
()()()( )() ()
2
ttt tt tt tt ttθ
++ +
⎡⎤
=− − − − +− + −
⎢⎥
⎣⎦
rgvr (10.1.23)

MECHANICAL SYSTEMS, CLASSICAL MODELS
606
or by the relation
121 121
1
() ( )(2 ) ( )
2
tttttttt
=
−− −−+− +rgvr,
[
]
12
,ttt
∈
. (10.1.23')
The velocity reads
22
() ( )ttt=− +vgv,
[
]
12
,ttt
∈
. (10.1.23'')
1.2 General theorems
In the following, we introduce some mechanical quantities (moment, moment of
momentum, work, kinetic energy, impulse of the force, impulse of the moment of the
force) in the frame of the theory of distributions. This allows the statement of the
general theorems corresponding to motions with discontinuous characteristics or to the
case of elastic collisions.
1.2.1 Momentum. Moment of momentum. Work. Kinetic energy
The momentum
() ()tmt
=
Hv (10.1.24)
of a particle is a continuous function in the considered interval of time
[
]
,tt
′′′
,
excepting the moments
i
t
, 1,2,...,in
=
, where appear discontinuities of the first
species. The jump of the momentum at the moment of discontinuity
i
t
is given by
[
]
() ( 0) ( 0)
ii i i
mmt tΔ= = +− −HV v v , (10.1.24')
being expressed by means of the velocity at the same moment.
We introduce also the quantities
()d
t
t
tt
′′
′
∫
F ,
()d
t
t
tt
′′
′
∫
F , ()d
t
c
t
tt
′′
′
∫
F , (10.1.25)
which represent the impulse of the generalized force, of the force in the usual sense and
of the complementary force, respectively, in the time interval
[
]
,tt
′
′′
; we have adopted
classical notations for the first and the third of these quantities, to have a uniform
symbolism, although the respective integrals have not sense, in general, from the point
of view of the theory of distributions. Observing that
11
d()d
nn
tt
c
ii i
tt
ii
tmtttmδ
′′ ′′
′′
==
=−=
∑∑
∫∫
FV V
, ttt
′
′′
<
< ,
and taking into account (10.1.5'), we may write
1
()d ()d ( )
n
tt
i
tt
i
tt tt
′′ ′′
′′
=
=+Δ
∑
∫∫
FF H, (10.1.26)
Other considerations on particle dynamics
607
wherefrom we state
Theorem 10.1.5 (theorem of impulse of the generalized force). The impulse of the
generalized force which acts upon a particle, in a certain time interval, is equal to the
sum of the impulse of the force in the usual sense, which acts upon that particle, in the
same time interval, and the sum of the jumps of the momentum of the particle,
corresponding to the moments of discontinuity.
In case of the problem considered in Subsec. 1.1.1 we may write (
0t
′
= ,
0
tt
′′
=
)
0
0
121
0
()d sin ( )
t
tt mgt mα=+−
∫
Fuvv.
The moment of momentum of a particle is introduced by means of the relation
[
]
() () () () ()
O
ttttmt=× =×KrHr v; (10.1.27)
its jump at the moment of discontinuity
i
t
is given by
() ()(0) ()(0) () ()()
ii i i i iii i
O
mt t mt t mt tΔ= ×+− ×−= ×=×ΔKrv rv rVrH
(10.1.27')
and is expressed with the aid of the jump of the momentum (or of the jump of the
velocity) at the same moment.
We introduce also the quantities
(())d
t
O
t
tt
′′
′
∫
MF ,
(())d
t
O
t
tt
′′
′
∫
MF , (())d
t
c
O
t
tt
′′
′
∫
MF , (10.1.28)
which represent the impulse of the moment of the generalized force, of the moment of
the force in the usual sense and of the moment of the complementary force, respectively,
in the time interval
[
]
,tt
′′′
. In general, the first and the third of these integrals have no
sense from the point of view of the theory of distributions; but we adopted classical
notations, so as to have a uniform symbolism. Starting from the relation (10.1.5'), we
can write
( ( ))d ( ( ))d ( ( ))d
ttt
c
OOO
ttt
tt tt tt
′′ ′′ ′′
′′′
=+
∫∫∫
MF MF MF
and are led to
1
(())d (())d ( )
n
tt
i
OO O
tt
i
tt tt
′′ ′′
′′
=
=+Δ
∑
∫∫
MF MF K ; (10.1.29)
thus, we may state
Theorem 10.1.6 (theorem of impulse of the moment of the generalized force). The
impulse of the moment with respect to a given pole of the generalized force, which acts
upon a particle, in a certain time interval, is equal to the sum of the impulse of the
moment with respect to the same pole of the force in the usual sense, which acts upon

MECHANICAL SYSTEMS, CLASSICAL MODELS
608
that particle, in the same time interval, and the sum of the jumps of the moment of
momentum of the particle, corresponding to the moments of discontinuity.
In case of the problem in Subsec. 1.1.1, we can write
[]
00
0
21
00
() ()d () ()d ( ) ( )
tt
ttt ttttm×=×+×−
∫∫
rF rF r vv
0
2
0
() ()d ( )
t
tttABm=×+×
∫
rF v,
assuming that the point
A is chosen as pole of the position vectors.
The work effected by the force
()tF in the interval of time
[
]
,tt
′
′′
is given by
() d()
t
t
Wtt
′′
′
=⋅
∫
Fr
; (10.1.30)
we introduce the notations
() d()
t
F
t
Wtt
′′
′
=⋅
∫
Fr,
() d()
t
F
t
Wtt
′′
′
=⋅
∫
Fr, () d()
c
t
c
F
t
Wtt
′′
′
=⋅
∫
Fr, (10.1.31)
where
F
W is the work of the generalized force ()tF ,
F
W is the work of the force in
the usual sense
()tF and
c
F
W is the work of the complementary force ()
c
tF , in the
time interval
[
]
,tt
′′′
. The first and the third of these integrals have no sense from the
point of view of the theory of distributions; but for the uniformity of the symbolism we
adopt these classical notations. Taking into account (10.1.5'), we may write
c
FF
F
WWW
=
+ , (10.1.31')
obtaining thus
Theorem 10.1.7 (theorem of work). The work of the generalized force which acts upon
a particle in a certain time interval is the sum of the work of the force in the usual
sense, which acts upon that particle, in the same time interval, and the work of the
complementary force, which acts upon the same particle in the considered time
interval.
The kinetic energy of the particle is given by the relation
2
1
()
2
Tmvt=
. (10.1.32)
If
i
t is a moment of discontinuity, then we may write the relations
2
2
00
11
lim ( ) lim ( ) ( 0)
22
ii
i
tt tt
Tt m vt mv t
→± →±
⎡⎤
==±
⎢⎥
⎣⎦
(10.1.32')
hence, there results that the moments of discontinuity of the velocity are the moments of
discontinuity of the kinetic energy too. We obtain, as well,
Other considerations on particle dynamics
609
22
1
() ( 0) ( 0)
2
iii
T mvt vtΔ= +− −
⎡
⎤
⎣
⎦
. (10.1.32'')
1.2.2 General theorems in case of motions with discontinuous characteristics
The second principle of mechanics takes the form
[]
dd
() () ()
dd
tmt t
tt
==FvH
(10.1.33)
in the frame of the theory of distributions; if discontinuities (in the usual sense) do not
appear, then it becomes
[]
dd
() () ()
dd
tmt t
tt
==
FvH. (10.1.33')
We notice that
1
dd
() () ( ) ( )
dd
n
ii
i
tt tt
tt
δ
=
=+Δ−
∑
HH H ,
where the jump of the momentum is given by (10.1.24'); taking into account also the
relation
1
()( )
n
c
ii
i
ttδ
=
=Δ −
∑
FH , (10.1.34)
which gives the complementary force, we find the relation
d
() () () ()
d
c
ttt t
t
==+HFFF
, (10.1.35)
being thus led to
Theorem 10.1.8 (theorem of momentum). The derivative with respect to time, in the
sense of the theory of distributions, of the momentum of a free particle is equal to the
generalized force which acts upon that particle.
As we have seen in Subsec. 1.1.4, if the particle is subjected to bilateral constraints,
then we must introduce the generalized constraint force (in the sense of the theory of
distributions)
()tR , given by
() () ()
c
tt t=+RRR, (10.1.36)
where
()tR is the constraint force in the usual sense, while ()
c
tR is the
complementary constraint force due to the discontinuities. In this case, the theorem of
momentum takes the form

MECHANICAL SYSTEMS, CLASSICAL MODELS
610
d
() () ()
d
ttt
t
=+HFR
. (10.1.35')
The complementary constraint force is expressed in the form
11
() () ( )
nn
c
ic i i
ii
ttmttδ
==
== −
∑∑
RR V.
Returning to the problem in Subsec. 1.1.1, we notice that the constraint force at the
point
B is given by
00
21
()( )()mtt m ttδδ=−=−−RV vv .
If we have
1k =
in the relation (10.1.2) (perfect elastic collision), then it results
21
=vv; the jump of the constraint force will have as direction the internal bisectrix
of
ABC , while the trajectory will be tangent to the external bisectrix. If
0k =
(perfect plastic collision), then we have
2
=
v0
(the second limit case).
If the velocity and the acceleration are continuous functions (in the usual sense), then
we can write the theorem of moment of momentum in the form
d
() () () ( ())
d
OO
ttt t
t
=× =
KrFMF.
But if the velocity and the acceleration have discontinuities of the first species, then we
notice that the moment of momentum
()
O
tK and its derivative in the sense of the
theory of distributions have the same moments of discontinuity; we may write
1
dd
() () ( ) ( )
dd
n
ii
OO O
i
tt tt
tt
δ
=
=+Δ−
∑
KK K ,
where the jump of the moment of momentum is given by (10.1.27'). In this case, we get
d
( ) ( ( )) ( ( )) ( ( ))
d
c
OO O O
tt t t
t
==+KMFMFMF
, (10.1.37)
the moment of the complementary force being given by
11
(()) ()( )( ) ( )( )
nn
c
iii ii
OO
ii
t t tt ttδδ
==
=×Δ−=Δ−
∑∑
MF r H K
. (10.1.38)
In this case, we can state
Theorem 10.1.9 (theorem of moment of momentum). The derivative with respect to
time, in the sense of the theory of distributions, of the moment of momentum with
respect to a given pole of a free particle is equal to the moment, with respect to the
same pole, of the generalized force which acts upon the respective particle.

Other considerations on particle dynamics
611
Introducing the generalized force too, in case of a particle subjected to bilateral
constraints, the theorem of moment of momentum takes the form
d
( ) ( ( )) ( ( ))
d
OO O
tt t
t
=+KMFMR. (10.1.37')
In the classical case (in the usual sense), the theorem of kinetic energy has the finite
form
() ()WTt Tt
′
′′
=
− .
For the derivative with respect to time of the kinetic energy we may write
1
dd
() () ( ) ( )
dd
n
ii
i
Tt Tt T t t
tt
δ
=
=+Δ−
∑
,
where the jump of the kinetic energy, corresponding to the moment of discontinuity
i
t
,
is given by (10.1.32''). Using the relation (10.1.31), we obtain
1
d
()d ( ) ( )d
d
n
tt
ii
F
tt
i
WTtt Tttt
t
δ
′′ ′′
′′
=
=+Δ−
∑
∫∫
,
wherefrom
1
() () ( )
n
i
F
i
WTtTt T
=
′′ ′
=−+Δ
∑
. (10.1.39)
We notice thus that the complementary work is just the jump of the kinetic energy at the
respective moment of discontinuity. We may state
Theorem 10.1.10 (theorem of kinetic energy in finite form). The work of the
generalized force which acts upon a particle in a certain interval of time is equal to the
sum of the difference between the kinetic energy at the final moment and the kinetic
energy at the initial one and the sum of the jumps of the kinetic energy of that particle,
corresponding to the moments of discontinuity.
In case of the problem considered in Subsec. 1.1.1, we have
()
0
22
0
21
0
1
sin d ( ) sin
2
t
F
WmgrTmgAB mvvαα=+Δ=+−
∫
;
if
1k = (perfect elastic collision), then the jump of the kinetic energy vanishes.
1.2.3 General theorems in case of elastic collisions
Starting from the notion of generalized force and of impulse of the generalized force,
we introduce the notion of percussion of a particle, by means of the definition formula

MECHANICAL SYSTEMS, CLASSICAL MODELS
612
00
lim ( )d
t
t
tt
tt
′′
′
′′ ′
−→+
=
∫
PF, (10.1.40)
where the limit is considered in the sense of the theory of distributions. Obviously,
neither in this case the integral written above has not sense from the point of view of the
theory of distributions; but we use this symbolism, to be closer to the classical one. We
assume, as well, that the time interval
[
]
,tt
′
′′
contains only one moment of
discontinuity
0
t and is thus that tt ε
′
′′
−
< , 0ε > arbitrary. In this case, we have
not to do with usual forces, but with generalized ones, more precisely, the distribution
0
()ttδ − appears; thus, the phenomenon of collision is no more introduced in
mechanics as a special phenomenon, but as a usual one, where the principles of
mechanics are applied in the conditions enounced in Subsec. 1.1.2.
Using a mean value theorem, we may write
00
lim ( )d
t
t
tt
tt
′′
′
′′ ′
−→+
=
∫
F0,
()
00
lim ( ) d
t
O
t
tt
tt
′′
′
′′ ′
−→+
=
∫
MF 0.
Hence, the impulse of the force and the impulse of the moment of the force in the usual
sense are quantities which can be neglected with respect to the impulse of the
complementary force and of the moment of the complementary force due to the
discontinuities, respectively; it results
0
00
lim ( )d
t
t
tt
tt m
′′
′
′′ ′
−→+
=
∫
Fv,
()
00
00
lim ( ) d ( )
t
O
t
tt
tt m
′′
′
′′ ′
−→+
=×
∫
MF r v,
where
0
r is the position vector corresponding to the moment of discontinuity, while
0
v
is the jump of the velocity, corresponding to the same moment. The Theorem 10.1.8
takes the form
0
()
Δ
=HP, (10.1.41)
so that we may state
Theorem 10.1.11 (theorem of momentum). The jump of the momentum of a free
particle at a moment of discontinuity is equal to the percussion which acts upon that
particle at the same moment.
Using the Theorem 10.1.9 and the notation (10.1.40), we get
00 00
() ()
O
Δ=×Δ=×KrHrP; (10.1.42)
thus, we state
Theorem 10.1.12 (theorem of moment of momentum). The jump of the moment of
momentum with respect to a given pole of a free particle (which is equal to the moment
with respect to that pole of the jump of the momentum of the particle) at a moment of
discontinuity is equal to the moment with respect to the same pole of the percussion
which acts upon that particle at the same moment.
