Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

572

the case in which

0k > the particle moves along the hyperbola branch which

surrounds the centre of attraction

′

(Fig.9.10,a), while, if 0k

, then the particle

moves along the other hyperbola branch (Fig.9.10,b); in each of the mentioned cases,

the other branch of the hyperbola leads to

(as in the case in Fig.9.2,b). We notice

that

min

/(1 ) ( 1)rpeae c

+= −< for 0k > and

min

/( 1)rpe

− (1 )ae=+

c> if 0k

; the apsidal point is reached only once by the particle during the motion

along the trajectory. Taking into account (9.2.23'), it results the remarkable form (for

0k > )

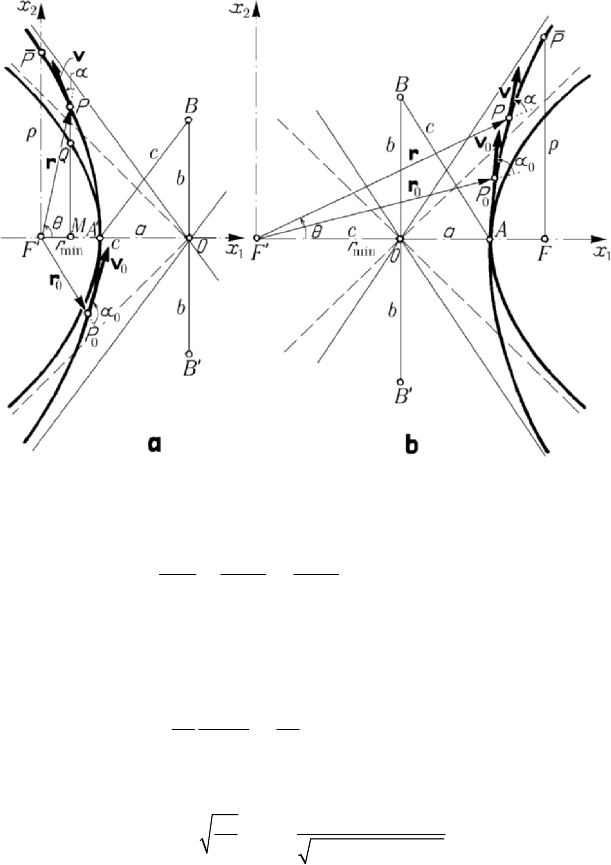
Figure 9.10. Hyperbolic motion due to the potential () /Ur k r

Case

0k > (a); case 0k

(b).

mv fmM fmM

−=

(9.2.23

)

for the conservation theorem of mechanical energy.

The law of motion along a hyperbola branch is given by the equation (9.2.10). The

relations (9.1.1') and (9.2.23') allow to write (for

0k > )

2kah

()

222

hp h

Cae

==−

−

min

(1)rae

− ,

wherefrom

222

(1)

()

aae

ρρ

−

+−

∫

;

Newtonian theory of universal attraction

573

the change of variable

(cosh 1)ae uρ =− leads to

(cosh 1)d

tt a e u u

=+ −

∫

Finally, we obtain the equation

sinh ( )euuntt

−

=−,

(9.2.24)

analogous to Kepler’s one for the elliptic motion,

n being given by (9.2.17); in this

case, the parameter

(,)u

∈

−∞ ∞ corresponds to the parametric equations

coshxOM a u==−

sinhxMQa u==

of the rectangular hyperbola with the

same centre

O and the same semiaxis a (Fig.9.10,a). Taking into account the relations

(cosh 1)rae u=−, cosh cosaucrθ

−

(9.2.25)

and the equation of the hyperbola, we get the Cartesian co-ordinates (Fig.9.10,a)

(cosh)xae u=− ,

1sinhxae u=− .

(9.2.25')

It results

cosh

cos

(cosh 1)

ca u

ae u

−

(9.2.25'')

wherefrom we obtain the relation between the angle

θ and the parameter u in the form

tan tanh

212

θ +

−

(9.2.26)

One can use also the equation (9.2.16) to study the motion of the particle along the

trajectory; we have

0γ < , because 1e > . In this case

()

arg tanh

γη

=−

−

∫

;

by the change of variable

(

)

tanh /2uγη

−

= , we may write

()

3/2

( ) (sinh ) (sinh )

(1) 1

tt e uu e uu

pee

−= −= −

+−−

−

obtaining thus an equation equivalent to the equation (9.2.24).

MECHANICAL SYSTEMS, CLASSICAL MODELS

574

In the particular motion on a rectangular hyperbola we have

, so that pa= ,

while

()

(

)

()

tan /2 1 2 tanh / 2uθ =+ .

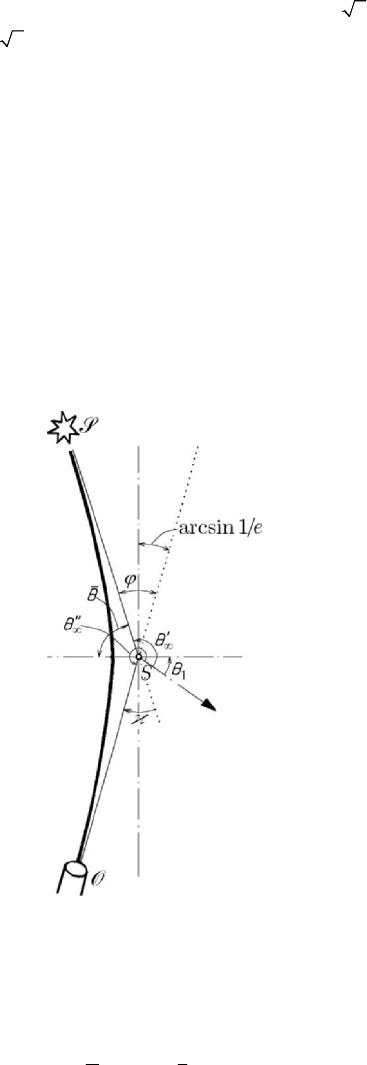
2.1.6 Deviation of the light ray

Starting from observations, it was stated that a light ray coming from a star

S far

off, its path passing in the vicinity of the Sun

S , is deviated; its final direction (for the

observer

O ) makes an angle ϕ with its first direction. We consider thus the trajectory

of a photon, assuming that this one, modelled as a particle, has a mass. The photon

describes a conic in its motion in the gravitational field of the Sun. Assuming that the

photon passes very close to the surface of the Sun (Fig.9.11), we may take

6.96 10 mr =⋅ , corresponding to Sun’s radius (any point of the trajectory may be

taken as initial position, in particular the apsidal point); as well,

310 m/sv =⋅ (the

velocity of light in vacuum), while

210 gM =⋅ (Sun’s mass). The inequality

2rv fM> is satisfied, so that the trajectory of the photon is an arc of hyperbola.

Figure 9.11. Deviation of the light ray.

From the equation (9.2.6) it results that the two asymptotes are specified by the

equation

1cos( )0e θθ+−=, which has always solutions, because

1e >

. The

angles

∞

, corresponding to the two asymptotes, are given by

(

)

arcsin

2 e

θθ

∞

=± + ;

(9.2.27)

Newtonian theory of universal attraction

575

we may write (Fig.9.11)

arcsin

2 e

θθ

∞

′

=++

arcsin

2 e

θθ

∞

′′

=+ −

(9.2.27')

too. We notice that each asymptote makes an angle equal to

(

)

arcsin 1/ 1/ee≅ with

the imaginary axis of the hyperbola; hence, the angle made by the two asymptotes,

equal to the angle

ϕ , corresponding to the deviation of the light ray, is given by

2arcsin

≅ .

(9.2.27'')

However, this formula could be obtained also by using the results in Chap. 8, Subsec.

1.2.1 concerning the phenomenon of diffraction. In our case, the diffraction angle

(Fig.9.11) is given by

[

]

22()2()πθ π πθθ π θθ

∞∞

′′

=− + =− + − − = − −



;

from

(

)

sin /2 cos( ) 1/eθθ

∞

′

=−=−



it results 2/e

≅

−



, the angle of

diffraction being negative, because the centre

S (the Sun) is of attraction. We notice

that

ϕ=



Because at the apsis the velocity is normal to the radius vector (which starts from

S ), we have

/2απ= ; in this case, from (9.2.7') it results (e is of an order of

magnitude

10 )

00 00

rv rv

MfM

=−≅

(9.2.28)

We may write

ϕ ≅

;

(9.2.28')

numerically, we obtain

0.87 sϕ ≅

Astronomical observations of great precision made during the total solar eclipses (for

the first time in May 1919), to may “catch” the light ray coming from the star

S, have

put in evidence a double angle (

1.74 sϕ

≅

), obtaining thus a new non-concordance of

the Newtonian model with the physical reality (besides the secular displacement of

Mercury’s perihelion, see Subsec. 2.1.4). However, one cannot be sure if these non-

concordances are due to Newton’s laws or to the Newtonian theory of gravitation (or to

both mathematical models); some direct improvements of those models did not lead to

convenient results, excepting the invariantive model built up by O. Onicescu (see Chap.

21, Sec. 3.2). These contradictions disappear in the frame of the general theory of

relativity elaborated by A. Einstein.

MECHANICAL SYSTEMS, CLASSICAL MODELS

576

2.1.7 Parabolic motion

If 0h = (we can have only 0k > , e.g., kfmM

), then the trajectory of a particle

acted upon by a Newtonian force of attraction is a parabola. Observing that

1e =

, the

equation (9.2.5') takes the form (Fig.9.12)

(

)

xpx=− −

(9.2.29)

in the parabolic motion; the distance to the pericentre is given by

Figure 9.12. Parabolic motion due to the potential () /Ur k r

22 2

00 0

min

sin

22 2

MfM

== =

(9.2.29')

The conservation theorem of mechanical energy takes the form

mv fmM

(9.2.30)

The formula (9.2.10) leads to

ρρ

−

∫

wherefrom we get

() /2

tt rprp

=+ + −

(9.2.31)

Newtonian theory of universal attraction

577

The equation (9.2.6) becomes (we consider the most general case in which

0θ ≠ and

use the true anomaly

ψθθ=−)

(

)

1tan

1cos 2 2

2cos

ppp

===+

(9.2.29'')

so that

(

)

tan 1 tan

2232

ψψ

=+ +

(9.2.31')

Starting from (9.2.9'), we obtain

()

1d2/d

Mp tηη+=

; observing that

(

)

tan /2ηψ= , we find again the above results. Using the co-ordinates

cosxrψ= ,

sinxrψ= , we get the Cartesian parametric equations of the trajectory

()

x η=−

xpη

(9.2.29''')

The equation (9.2.31') has only one real root

(

)

tan /2ψ for a given

. The moment

is obtained for

0t =

; if

, then one cannot have 0ψ

, so that the particle

starts from the initial position and describes an arc of parabola towards infinity, without

passing through its vertex.

2.1.8 Motion of comets

Newton’s research has been extended also on the comets known at his time,

especially on the Halley comet, appeared in 1680; he assimilated thus the trajectories of

the comets to very elongated ellipses, to which Kepler’s laws may be applied. Based on

Halley’s observations, Newton concluded that in case of comets too we have

/constCp= , being thus led to the same law of universal attraction. Hence, the law

of motion is that obtained in Subsec. 2.1.2, and the motion of a comet may be also a

parabolic one; corresponding to the results of the preceding subsection, the Sun is at

one of the foci, as it was shown by Newton. The theorem of areas may be applied too.

The co-ordinates which specify the parabolic trajectory of a comet are

,, ,it

Ωω and

the perihelion distance

/2p , hence only five independent parameters.

2.2 Problem of artificial satellites of the Earth and of interplanetary

vehicles

Using the results obtained in the preceding subsection, we consider, in what follows,

the problem of the artificial satellites of the Earth and of the interplanetary vehicles; we

may thus put in evidence the cosmic velocities, the conditions of non-returning on the

Earth, the conditions to become a satellite, and the conditions to escape in the cosmic

space. As well, we make the study of the orbit of an artificial satellite.

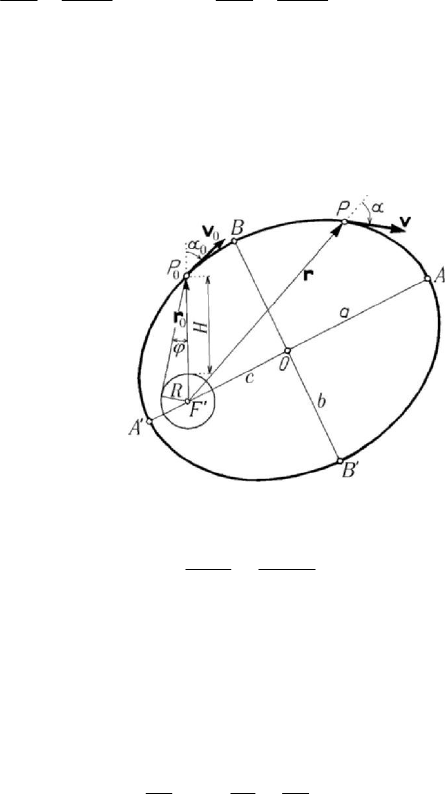
MECHANICAL SYSTEMS, CLASSICAL MODELS

578

2.2.1 Theory of artificial satellites of the Earth. Conditions to become a satellite

The general theory presented in Subsec. 2.1.2 may be used to study the launching

and the motion of the artificial satellites of the Earth. To this goal, we assume that the

Earth is a sphere of radius

R , its mass being distributed with spherical geometry. If M

is the mass of the Earth, in conformity with the formula (1.1.85) we may write

MgR= . In this case, the conservation theorem of mechanical energy takes the form

mv mgR

−=

mgR

=−

rRH

+ ;

(9.2.32)

we assume that the satellite

P , modelled as a particle of mass m , is unbound from the

launching rocket at the height

H from Earth’s surface, along the local vertical, at the

point

P of position vector

r , the initial velocity being

v (Fig.9.13). To obtain thus a

satellite of the Earth, the trajectory of the particle

P must be an ellipse; in this case

0h < , so that the initial velocity fulfils the condition

Figure 9.13. Launching of an artificial satellite of the Earth.

22gR gR

rRH

(9.2.33)

The particle

P becomes a satellite if, supplementary, the distance to the perigee is at

least equal to the radius of the Earth (

min

rR≥ ). Taking into account the results in

Subsec. 2.1.3, we must have

(1 )aeR

−

≥ , wherefrom 1/eRa

≤

− . Because 0e ≥ ,

one must have

aR≥ too; associating the inequality (9.2.33) to (9.2.12'''), we have

finally,

rgRr

−≤ <

(9.2.33')

obtaining thus inferior and superior limits for the initial velocity.

Newtonian theory of universal attraction

579

Taking into account the first relation (9.2.12'), we may express the condition

(1 )aeR−≥ in the form /(1 )peR

≥ or /1pR e

−

≥ too; the first inequality

(9.2.33') ensures that

pR≥

(because, in this case 0e ≥ ), so that we may also write

()

/1pR e−≥. The first relation (9.2.7') leads to

(

)

11cot

ppp

⎛⎞

−≥ −+

⎜⎟

⎝⎠

;

using the relation (9.2.7), we get then

222

00 0

sin

gR R

⎛⎞

−≥−

⎜⎟

⎝⎠

(9.2.34)

Because

1/ 1/Rr≥ , it results that we must have

22 2

sinrRα ≥ too, wherefrom

sinrRα ≥ ; (9.2.34')

this relation states that the support of the velocity

v cannot pierce the Earth’s sphere

(at the limit, it may be tangent to it (Fig.9.12)). We notice that the relation

()

22 2

00 0

2( )

sin

Rr R

rr Rα

−

≥−

−

takes place; indeed, bringing to the same denominator, we read

00 00 0

( sin ) 2 sin (1 sin ) 0Rr Rrααα−+ −≥

The equality can take place only in case of a launching from the surface of the Earth,

tangent to it. From (9.2.33')-(9.2.34') it results

22 2

()

sin

Rr R

rgRr

−

≤<≤

−

(9.2.35)

in this case. These inequalities represent the conditions to become a satellite; the first

and the last inequality correspond to the non-returning on the Earth (to the escape from

the Earth), while the second inequality corresponds to the transformation of the body

launched from the surface of the Earth in a satellite of that one (elliptic trajectory).

If the satellite enters on the orbit under an incidence angle

/2απ

, then the

conditions (9.2.35) become (the last inequality is verified because

≤

)

00 0

RR R

rR r gR r

≤<

(9.2.35')

MECHANICAL SYSTEMS, CLASSICAL MODELS

580

while in the case in which

≅

, hence

≅

(the launching point is very close to

the surface of the Earth), we get

2gR v gR≤< .

(9.2.35'')

2.2.2 Cosmic velocities

The inequalities (9.2.35'') may be written in the form

III

vvv

≤

< , (9.2.36)

where we have introduced the first and the second cosmic velocities, respectively, given

vgR= ,

II I

22vgRv==;

(9.2.37)

taking

9.81 m/sg = and

6.38 10 mR =⋅ , we get

7.905 km/sv

and

11.179 km/sv = .

In general, the velocities for which a terrestrial body becomes a celestial one are

called cosmic velocities. The two velocities put here in evidence are called special

cosmic velocities. The first special cosmic velocity (the circular cosmic velocity)

represents the smallest velocity by which a body can be launched from the surface of

the Earth (tangent to it) without returning on the Earth; the second special cosmic

velocity (the parabolic cosmic velocity) is the greatest velocity by which a body may be

launched from the surface of the Earth so that to remain a satellite of it. Any cosmic

velocity contained between the two mentioned velocities leads to an elliptic trajectory.

A cosmic velocity equal to

v leads to a parabolic trajectory, while a cosmic velocity

greater than

v leads to a hyperbolic one. In the latter cases, the celestial body so

created can no more be a satellite of the Earth, having a non-bounded trajectory in the

interplanetary space; eventually, it can be captured by another celestial body in the

proximity of which may pass its trajectory.

The numerical results thus obtained have a certain degree of approximation; indeed,

we should take into account the whole system of particles which are involved in motion

(see Chap. 11 too), as well as the resistance of the atmosphere (on a trajectory of

200-300 km , till the satellite enters in the interplanetary space, where the resistance of

the air is negligible). In this order of ideas, if the entrance on the trajectory takes place

at a height

H (measured along the local vertical), then the conditions (9.2.35') lead to

(9.2.36) too, in the form

III

vvv≤<, with

III

00 0

(/)2

( ) 1 / (1 / )(1 /2 )

vvv

rRrRrHRHR

===

++ ++

()

(

)

319

432

⎡

⎤

=≅−+

⎢

⎥

⎣

⎦

(9.2.37')

Newtonian theory of universal attraction

581

(

)

II II II

RHH

vv v

rRR

⎡

⎤

== ≅−+

⎢

⎥

⎣

⎦

(9.2.37'')

Taking, e.g.,

210 mH =⋅ , we get

(1 0.02355 0.00059)

vv=− +

0.977v≅

7.723 km/s= and

II II

(1 0.01570 0.00037)

vv=− +

0.985v

≅

11.011 km/s= ,

hence velocities somewhat smaller. In general, we should take

()

II I

22 2

00 0

sin

(1 / ) (1 / ) sin 1

Rr R

vv v

rr R

HR HR

−

++ −

⎡

⎤

⎣

⎦

;

(9.2.37''')

obviously, the angle

α cannot be chosen arbitrarily, because the quantity under the

radical sign must be positive.

Returning to the conservation theorem of mechanical energy (9.2.32) and assuming

that a body (modelled as a particle) is launched from the Earth surface (

rR= ), we

may write

mv mgR

mgR

−=−

;

(9.2.38)

it results

(

)

(

)

22 22

21 1

vv gR vv

=− − =− − .

(9.2.38')

A particle can reach the point

P , at a distance r from the centre of the Earth

(Fig.9.13), with a velocity

≠

, only if

(

)

II II

RRR

vv v

rrr

⎡

⎤

≥− ≅− +

⎢

⎥

⎣

⎦

(9.2.39)

For instance, if

60rR= (the distance from the centre of the Earth to the centre of the

Moon), then we obtain

(1 0.00833 0.00003)vv≥− +

0.992 11.090 km/sv

≅

= .

In general, the cosmic velocities corresponding to an arbitrary celestial body, of mass

m , are given by

II I

vv= ,

(9.2.40)

where

r is the distance from the interplanetary vehicle to the centre of the considered

celestial body. These formulae are useful to establish the conditions in which a body

which is launched from the Earth surface and reaches a certain distance from another

celestial body (Moon, Sun etc.) becomes a satellite of that one or continues its