Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

552

From the formula (9.1.12) too, it results that the force obtained by applying the

operator gradient vanishes at infinity as

1/r . So, in the study of the solar system (the

motion of the planets around the Sun) one can neglect the action of other celestial

bodies, those ones being situated at distances practically infinite with respect to the

distances of the planets to the Sun or between them.

The properties i)-iv) characterize the Newtonian potential. Indeed, if there exists

another potential

()U

′

r which has these properties, then () ()UU

′

−

rr is a harmonic

function in the whole space, vanishing at infinity; from the theorem of maximum of

harmonic functions it results that the two potentials differ by a constant, which –

obviously – is equal to zero.

1.2.2 Potential of simple stratum of a homogeneous sphere

In case of a homogeneous sphere, the potential of simple stratum is given by the

surface integral

()

μ=

∫

r , R

−r

(9.1.13)

where the equation of the sphere

S of radius

ξ reads

ξξ

. Because of spherical

symmetry, the potential depends only on the distance from the attracted particle to the

centre of the sphere, so that

()UU

r , rOP==

JJG

r . Choosing the point P on the

Ox -axis and using spherical co-ordinates (colatitude θ and longitude ϕ ) for Q ∈ S ,

we may write (

222

2cosRr rξξθ=+− )

22 22

00 00

sin d d

sin d

() d

2cos 2cos

rr rr

ππ

ξ θθϕ

θθ

μμϕ

ξξθ ξξθ

+− +−

∫∫ ∫ ∫

()

00 0

000

2cos 2

ξξθ πμξ

πμξ ξ ξ

+−

==+−−

000

4 for ,

4 for ;

πμ ξ

πμξ ξ ξ

πμ ξ

⎧

−≤−

⎪

=−≤≤

⎨

⎪

≥

⎪

⎩

observing that the total superficial mass is

4m πμξ= , it results

for exterior to the sphere ,

() ()

const otherwise.

UUr

⎧

⎪

⎨

⎪

⎩

(9.1.14)

Newtonian theory of universal attraction

553

We can thus state that a particle situated outside the homogeneous sphere

S is

attracted towards its centre as if the whole superficial mass of attraction would be

concentrated at this point (corresponding to the property iv) in the preceding

subsection); if the particle is situated on the sphere or in its interior, no force of

attraction is acting upon it. The potential

()U r is harmonic ( 0U

= ) in the whole

space and vanishes at infinity.

We notice also that

/Un∂∂ has a jump by passing through the surface S (the

normal derivative is equal to

4πμ

−

if P tends to S from the exterior and is equal to

zero for

P tending to S from the interior), although ()U r is a continuous function in

the whole space.

1.2.3 Volume potential of a homogeneous sphere

The volume potential of the homogeneous sphere

(0, )S ξ is given by (9.1.8''); with

the same observations as at the preceding subsection, we may write (we use spherical

co-ordinates

,,ξθϕ too; for P at the interior of the sphere S we make a separate

integration, as

0 rξ≤≤ or as

r ξξ

≤

≤ )

22 22

00 0

sin d d d sin d

() d d

2cos 2cos

rr rr

πξ π

ξθξθϕ θθ

μμϕξξ

ξξθ ξξθ

+− +−

∫∫∫ ∫ ∫ ∫

()

drr

πμ

ξξ ξξ=+−−

∫

2 for interior to the sphere ,

otherwise.

πμ ξ

πμ

⎧⎛ ⎞

−

⎜⎟

⎪

⎝⎠

⎨

⎪

⎩

Observing that the total mass is

4/3m πμξ=

, it results

3 for interior to the sphere ,

() ()

otherwise.

UUr

ξξ

⎧⎡ ⎤

⎛⎞

−

⎜⎟

⎪

⎢⎥

⎪

⎝⎠

⎣⎦

⎨

⎪

⎩

(9.1.15)

As in case of the potential of simple stratum, a particle situated outside the

homogeneous sphere

S is attracted by its centre as if the whole mass would be

concentrated at this point (Newton’s modelling of the celestial bodies as particles is

thus justified). The potential

()U r and its derivatives of first order are continuous

functions in the whole space; the derivatives of second order of this potential have

discontinuities by crossing the surface

S and U

is given by (9.1.10). For numerical

computations we may take

6.37827 10 mξ =⋅.

MECHANICAL SYSTEMS, CLASSICAL MODELS

554

In case of a homogeneous spherical stratum of mass

m , contained between two

spheres

S and

S of centre O and radii

ξ and

ξξ

, respectively, we can use the

parallelogram principle (independence of the action of forces), obtaining thus

(

)

()

2 for interior to the sphere ,

()

for exterior to the sphere ,

πμ ξ ξ

πμ

ξξ

−

⎧

⎪

⎨

−=

⎪

⎩

(9.1.16)

where

m is the mass of the spherical stratum. We are led to the same mechanical

conclusions as above.

We notice that we can obtain the same results for the volume potential starting from

the equation (9.1.10) written in spherical co-ordinates (

(

)

(

)

1/ (d/d ) d/drrrrΔ=

in case of spherical symmetry, corresponding to the formula (A.2.42')). For instance, in

case of the volume potential of the sphere

(0, )S ξ we have

d()

⎛⎞

⎜⎟

⎝⎠

wherefrom

() /Ur C r C=+,

,constCC

; from (9.1.12) it results that

Cm=

0C =

1.2.4 Potential of the terrestrial spheroid

In a better approximation, the Earth must be considered as a spheroid. Taking into

account the Maclaurin series in Subsec. 1.2.1, the volume potential is given by

() (cos )()d

UPV

ξψμξ

∞

∑

∫∫∫

r ,

(9.1.17)

for a particle

in the exterior of the Earth attractive mass. Corresponding to the first

two Legendre polynomials, we notice that (the mass of the Earth and its static moment

with respect to a plane normal to

and passing through the pole

– centre of the

Earth)

()d

Vmμξ =

∫∫∫

, cos ( )d 0

Vξψμξ

∫∫∫

;

the third Legendre polynomial leads to

() ()

22 2 2

3cos 1 ( )d 2 3sin ( )d 2 3

VVII

ξ ψ μξ ξ ψ μξ−=− =−

∫∫∫ ∫∫∫

where

I is the polar moment of inertia of the Earth with respect to its centre, while I

is the axial moment of inertia with respect to OP . Choosing the principal axes of

inertia

2O and 3O in the equatorial plane and the axis 1O along the axis of the Earth (so

that

123

III>>), we may write (we use the formulae (3.1.23) and (3.1.82''))

Newtonian theory of universal attraction

555

123

IIII=++ and

222

11 22 33

I InInIn

=++, where

n , 1, 2, 3i

, are the

direction cosines of the straight line

with respect to these axes; in spherical co-

ordinates, we have

cosn θ=

sin cosn θϕ

sin sinn θϕ

, so that

(

)

(

)

(

)

222 22

12 3

2 3 1 3 cos 1 3sin cos 1 3sin sin

III I I

θθϕθϕ−= − + − + −

()

123

1 3 cos sin cos 2

III

θθϕ

⎛⎞

=− − − −

⎜⎟

⎝⎠

Calculating the principal moments of inertia of the Earth, we get

231

()/10/3III

−

−<

; in this case, we may assume that

II≅ (which

corresponds to the spheroidal model accepted for the Earth). Thus, we deduce

(

)

() () ( ) cos

UUr II

θ==+ − −r ,

(9.1.18)

where

m is the mass of the Earth.

In case of the spherical model of the Earth, we find again the result in the preceding

subsection (formula (9.1.15)).

For a more exact result, one may use the polynomial

(cos )P ψ too.

These results are very important in the study of the motion of artificial satellites of

the Earth.

2. Motion due to the action of Newtonian forces of attraction

We have seen that, in the classical model of mechanical systems, the celestial bodies

are subjected only to the action of internal forces (forces of Newtonian attraction). This

allows a study of the motion of planets, of artificial satellites of the Earth, of

interplanetary vehicles, as well as of other types of motion at the atomic level etc. We

notice that we will study, e.g., the motion of a celestial body (modelled as a particle)

with respect to another celestial body, considered as fixed, hence the motion of a

particle subjected to the action of a central force.

2.1 Motion of celestial bodies

After a general study of the motion of a particle acted upon by a central force of the

nature of a Newtonian attraction force (elliptic, hyperbolic or parabolic trajectories), we

will consider the motion of planets and comets; we put in evidence the deviation of the

light ray too.

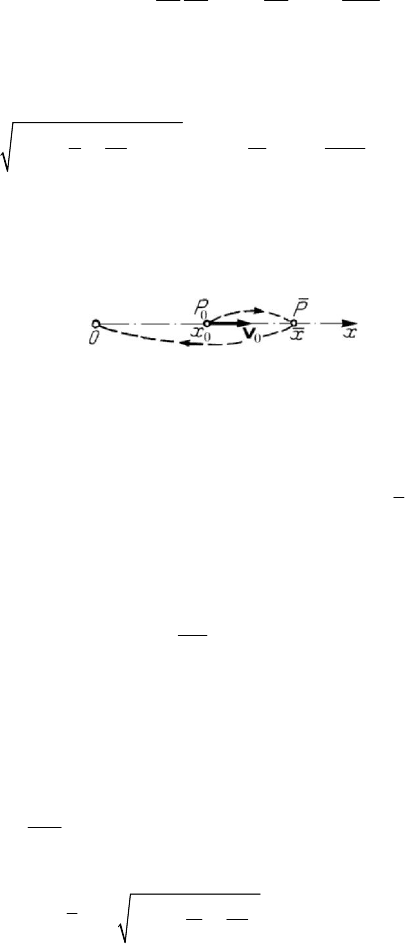
2.1.1 Rectilinear motion due to the action of a Newtonian force of attraction

If the initial velocity

v is directed along

JJJG

r , where

P is the initial position,

then (as we have seen in Chap. 8, Subsec. 1.1.2) the trajectory of the particle

P is

rectilinear; it is assumed that there exists a centre of attraction at

O (a particle of mass

M ), the particle P of mass m being subjected to a force of Newtonian attraction

MECHANICAL SYSTEMS, CLASSICAL MODELS

556

mMOP x=−

JJG

F (we choose the corresponding trajectory as Ox -axis). The

equation of motion

dd d

vx v mM

mx mv m mv f

xt x

== = =−





leads to

/2 /mv fmM x h=+, hence to a conservation law of mechanical energy, h

being the energy constant; the initial conditions (

(0)xx

(0)vv

) allow to write

2vfM v

⎛⎞

=± − +

⎜⎟

⎝⎠

mfM

⎛⎞

=−

⎜⎟

⎝⎠

(9.2.1)

We assume that

0x > (the positive direction of the Ox -axis is towards the initial

position); one cannot have

, from the mechanical point of view. One takes the

sign ± before the radical as

0v ≷ .

Figure 9.4. Rectilinear motion due to the action of a Newtonian force of attraction.

0v ≤

, then the particle comes near to the point

( d/d 0xt

) with a velocity

increasing in absolute value, which tends to infinity for

00x →+. If

0v >

, then

the particle moves away from the point

(d/d 0xt> ); if

0h ≥

, then the particle

tends to infinity, while if

it stops at the point of abscissa 2/xfMh

− , where

the velocity changes of sign and returns, as in the foregoing case (Fig.9.4).

Modelling the Earth as a particle of mass

and denoting

, where R is the

radius of the Earth, approximated as a sphere, the condition

0h ≥

leads to

≥

(9.2.2)

where we took into account (9.2.1). Introducing numerical values, we find that a

particle from the Earth surface must be launched up along the local vertical with an

initial velocity

vv≥ (

11.2 km/sv

≅

being the second cosmic velocity, see

Subsec. 2.2.2) so as not to return on the Earth; obviously, the resistance of the air has

been neglected.

In case of a particle which falls on the Earth without initial velocity from the initial

position

xx OP== , we obtain the velocity at the Earth surface (the falling

velocity)

2vfM

⎛⎞

=− −

⎜⎟

⎝⎠

;

(9.2.3)

Newtonian theory of universal attraction

557

xRH=+, HR , and if we take into account Torricelli’s formula (7.1.17),

then we find again the formula (1.1.85). Also from (9.2.1), one obtains the falling time

dd1

RR x

xx R

vxx

==− =

−

⎛⎞

−

⎜⎟

⎝⎠

∫∫ ∫

(9.2.3')

2.1.2 Curvilinear motion due to the action of a Newtonian force of attraction.

Newton’s problem. Runge-Lenz vector

Starting from the results obtained in Sec. 1.2, we may consider the motion of a

particle in a field of central forces given by a potential of the form

()

;

(9.2.4)

thus, the Newtonian gravitational field is of attraction (

0kfmM

> ), while the

Coulombian one (specified by (1.1.84'')) may be an attractive or a repulsive field,

depending on the relative signs of the charges in interaction (

0k >

0k <

respectively).

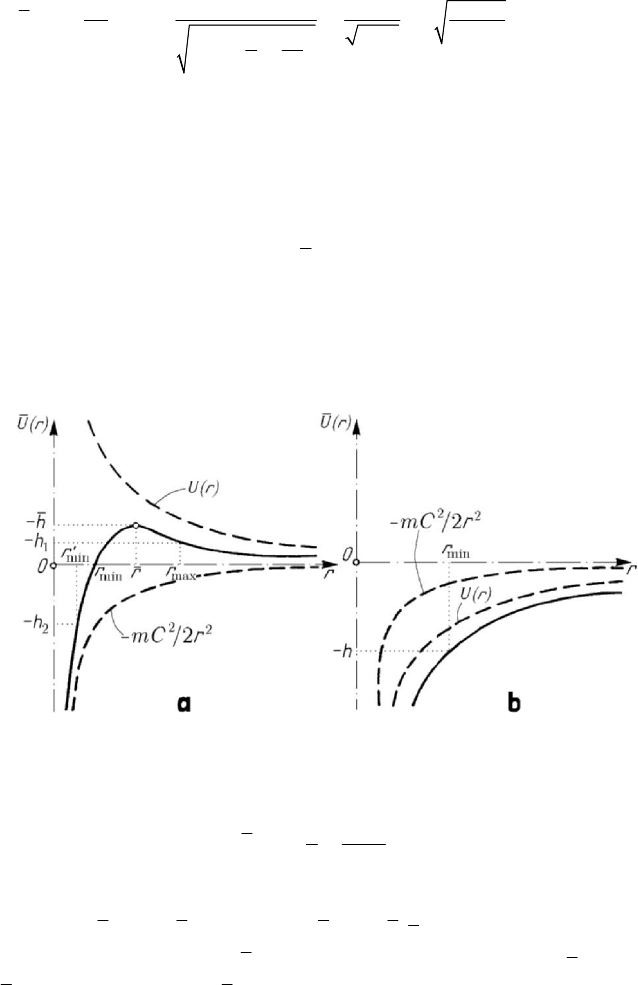
Figure 9.5. Apparent potential: attractive (a); repulsive (b).

We introduce the apparent potential (8.1.6') in the form

()

kmC

=−

In case of a potential of attraction (

0k > ), we represent the apparent potential in

Fig.9.5,a. At

()Ur h=− corresponds

max

()UUr= , the orbit being circular; an

elementary calculus shows that

/2hkmC=− , with an orbit radius

/rmCk= .

()Ur h≥− ,

0 hh<− <− , then the orbit is contained in the circular annulus of

MECHANICAL SYSTEMS, CLASSICAL MODELS

558

radii

min

r and

max

r , being a closed curve (in conformity to Bertrand’s theorem). For

()Ur h≥− ,

0h−<, we get a unbounded orbit with a pericentre at a distance

min

′

from the centre of attraction. In case of a repulsive potential (

), we represent the

apparent potential in Fig.9.5,b; for

()Ur h≥− , 0h

−

< , there result only unbounded

orbits of pericentres at the distance

min

r from the repulsive centre.

Let us consider now the case of a Newtonian potential of attraction. We choose the

Ox -axis so as to be an apsidal line; the formulae (8.1.6'), (8.1.6'') lead to the equation

of the trajectory in polar co-ordinates in the form (we take

0θ

)

min

24 2 2

d(1/ )

kmC

kh k

mC mC mC

⎛⎞

−+

+−−

⎜⎟

⎝⎠

∫∫

arccos

−

where we took into account that

min

corresponds to 0θ

. We obtain thus the

equation (9.1.1) of a conic, with

= ,

mC h

=+ .

(9.2.5)

Figure 9.6. Curvilinear motion due to the action of a Newtonian force of attraction.

In Cartesian co-ordinates, there results (we notice that

cosxrθ

) (Fig.9.6)

22 2

12 1

()0xx exp

−−=;

(9.2.5')

the conic pierces the co-ordinate axes at the points

min

(,0)r and (0, )p , obtaining thus

a geometric interpretation for the parameter of the conic too. Taking into account the

eccentricity, it is seen that the trajectory is an ellipse, a parabola or a hyperbola as

0h < , 0h

or 0h > , respectively; in particular, if

/2hkmC=−

, then we have

0e = , so that the ellipse is a circle.

Newtonian theory of universal attraction

559

We may obtain an equivalent form of this result starting from Binet’s equation

(8.1.4). Introducing the force of Newtonian attraction

/FfmMr=− , where M is

the mass of the attractive particle, we get the equation

(

)

d1 1

+= ,

wherefrom

cos( )

θ=−+,

,CC

being two scalar integration constants; with the notations

/Cep

C θ=

/pC fM=

, we find again the equation of the conic with respect to the focus

F and

an axis inclined by

θ towards the apsidal line, in the form

1cos( )

e θθ

+−

(9.2.6)

If we put the initial conditions at the moment

as in Chap. 8, Subsec. 1.1.1, then

we may express the conic parameter in the form

22 2

00 0

sinrv

MfM

(9.2.7)

We use the conditions (8.1.4'') to determine the eccentricity

e and the angle

θ ,

obtaining thus

1cos( )

θθ+−=,

sin( ) cot

θθ α−= ,

wherefrom

000

1cot1 2

sin

pp pp

⎛⎞

=−+ =+ −

⎜⎟

⎝⎠

22 2

00 0 00

sin

rv rv

fM fM

⎛⎞

=+ −

⎜⎟

⎝⎠

000 0 0

00 0

cot sin cos

tan( )

sin

prv

rv fM

ααα

θθ

−= =

−

(9.2.7')

Hence, the trajectory is an ellipse, a parabola or a hyperbola as

2rv fM< , as

2rv fM= or as

2rv fM> , respectively. The genus of the conic depends thus

MECHANICAL SYSTEMS, CLASSICAL MODELS

560

only on the initial distance to the centre of attraction (radius

r ), on the intensity of this

centre (mass

M ) and on the magnitude of the initial velocity (velocity

v ), but does

not depend on the direction of this velocity (angle

α ). For the condition 0e = , it

results (

/2απ= , so that

sin 1α

)

00 00

rv rv

fM fM

⎛⎞

−

=−

⎜⎟

⎝⎠

;

hence, the orbit is circular if

rv fM= . These conditions are equivalent to those

previously obtained, because the energy constant (the mechanical energy at the initial

moment) is given by

/2 /hmv fmMr=−

The angle

(, )α = ) rv (see Fig.8.1) is given by (

rCθ



)

tan

rCr

vrrr r

θθ

α ====





;

(9.2.8)

taking into account (9.2.6) we may also write

tan

sin( )

θθ

−

(9.2.8')

We denote

θθ= too, because for

θθ

we obtain

min

/(1 )rpe

+ , hence the

pericentre. The angle

ψθθ=− is called true anomaly, representing the angular

distance of the particle with respect to the pericentre.

From the law of areas it results

dddCt r rθψ==; taking into account the

equation of the conic

/(1 cos )rp e ψ=+ and its parameter

/pC fM= , we may

also write

3/2

(1 cos )

CfM

With the notation

tan

= ,

(9.2.9)

we obtain

cos

−

so that the law

()tηη= , hence the law ()tψψ

too, is given by the differential

equation with separate variables

Newtonian theory of universal attraction

561

(

)

()

3/2

(1 )

ηη

γη

−

(9.2.9')

which will be integrated taking into account the nature of the conic.

The formula (8.1.6''') allows to find the law of motion of the particle along the

trajectory in the form

min

kC h

−+

∫

(9.2.10)

In the study of Newton’s problem we used till now two first integrals, corresponding

to the conservation of the moment of momentum (a vector first integral, equivalent to

three scalar first integrals) and to the conservation of the mechanical energy (a scalar

first integral), respectively; hence, it results that the trajectory is a plane curve and that

one can determine the motion on it (from the first integral of areas, which is a

component of the first integral of moment of momentum, or from the first integral of

mechanical energy). The formula (8.1.6'') or Binet’s equation may be replaced by a

third first integral specific for a field of Newtonian attraction. In case of a central force

versF=Fr, (,;)FF t=



rr , we may write, starting from Newton’s equation

() ()

OOO

mm F

trr

×= × =×= ××

  

rK rK K r rr

where we took into account the conservation theorem of moment of momentum

(



); it results (we notice that rr

⋅



rr , in conformity to the formula (A.1.12))

(

)

() ()() ()

FF r

rFrr rF

tr r r

×=××= ⋅−= −=− −

⎡⎤

⎣⎦







rK r rr rrr r r r r

so that

(

)

()

ttr

×=−



Hence, if

constrF=

(in the above considered case

/FfmMr=−

), then we may

introduce the vector

=× −



rKR

(9.2.11)

called the Runge-Lenz vector, which is conserved in time along the trajectory of the

particle (

d/dt = 0R , hence const

JJJJG

), being a vector first integral of the motion,

equivalent to three scalar first integrals. One obtains thus seven scalar first integrals