Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

562

which are not independent (we may have at the most six independent first integrals for a

single particle). Observing the scalar product

⋅

=KR (two zero mixed products),

it results that the Runge-Lenz vector, applied at the pole

O of attraction, is contained in

the plane of the motion (because

⊥

KR ,

const

JJJJG

). Using the two previous first

integrals, we can write (

⊥



)

(

)

222

() 2

mC h

×= = +



rK rK ;

it results then (

()()

OOO

mmK×⋅=×⋅=



rK r rrK

)

(

)

2222

()2()

OOO

mM fmM f m M

×− =× − × ⋅+



rK rK rK

(

)

2 22 222 2 222

22 2

mM M

mC h f mC fmM mCh fmM

=+− +=+

so that

mMe

R ,

(9.2.11')

where we have introduced the eccentricity (9.2.5) (

kfmM

). Choosing the

Ox -axis

along the Runge-Lenz vector and denoting

(,)θ

) rR , we may write

cosr θ⋅=rRR ; as well, ()

mMr

⋅

=× ⋅−



rrK r

KmfmMr=−

mC=

mMr− . Equating the two expressions of the scalar product and taking into

account (9.2.7), (9.2.11'), we find again the equation (9.1.1) of the conic. The Runge-

Lenz vector allows thus to determine the equation of the trajectory on an algebraically

way, its direction being from the centre of attraction to the pericentre.

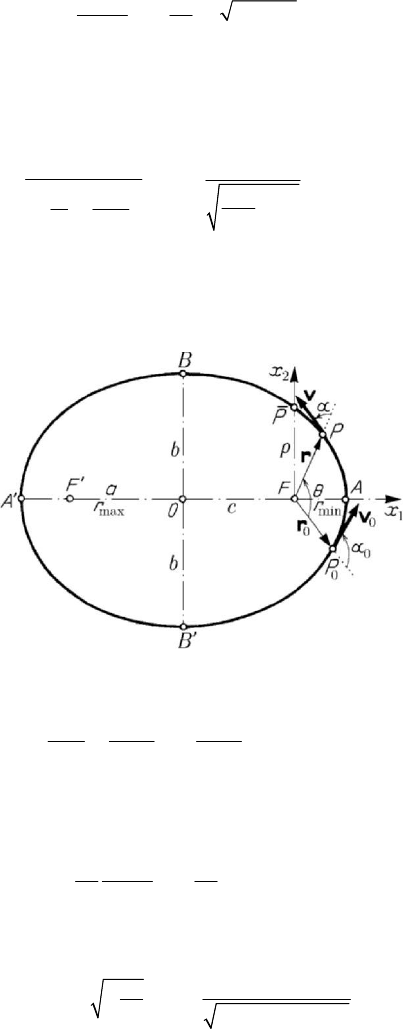
2.1.3 Elliptic motion. Kepler’s equation

0h <

, then the trajectory of the particle acted upon by a force of Newtonian

attraction (we can have only

0k >

, e.g., kfmM

) is an ellipse; in the elliptic motion

we write the equation (9.2.5') in the form

(

)

22 2 2

12 1

12ex x pex p−++= (we have

01e≤<). We notice that we may write this equation also in the form

()

xae

= ;

(9.2.12)

the semiaxes (Fig.9.7)

==−

−

==−

−

(9.2.12')

and the focal distance

Newtonian theory of universal attraction

563

pe ke

cae a b

== =−= −

−

(9.2.12'')

are thus put in evidence. We mention that, for a given potential (

k is given), the semi-

major axis of the ellipse depends only on the mechanical energy constant

h . We may

express the semiaxes of the ellipse by means of the initial conditions in the form

⎛⎞

−

⎜⎟

⎝⎠

00 0

sin

−

;

(9.2.12''')

thus, we notice that

a does not depend on the direction of the initial velocity (Fig.9.7).

From (9.2.12') it results that the conservation theorem of mechanical energy may be

written in the remarkable form

Figure 9.7. Elliptic motion due to the potential () /Ur k r

mv fmM fmM

−=−

(9.2.12

)

To can determine the law of motion along the ellipse, we use the equation (9.2.10).

From (9.1.1') and (9.2.12'), it results

2kah=− ,

()

222

hp h

Cae

=− =− −

−

min

(1 )rae

− ,

so that

22 2

(1 )

()

ae a

ρρ

−

=+−

−−

∫

;

by a change of variable

(1 cos )aeuρ =− , we may write

MECHANICAL SYSTEMS, CLASSICAL MODELS

564

(1 cos )d

tt a e uu

=+ − −

∫

wherefrom we get Kepler’s equation

(sin)

tt a ue u

=+ − .

(9.2.13)

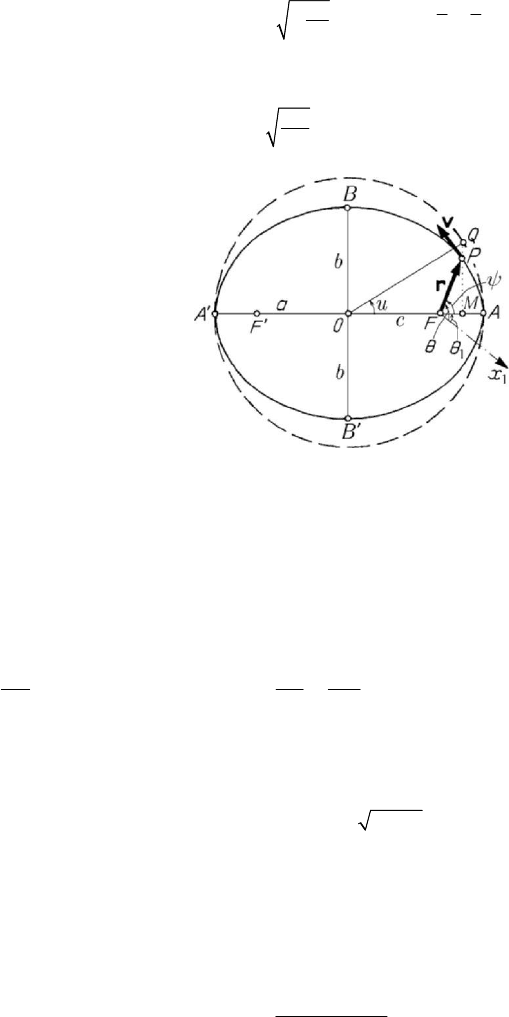
Figure 9.8. Elliptic motion in Kepler’s representation.

We assume now that, in general, the

Fx -axis does not coincide with the apsidal line

(

0θ ≠ , Fig.9.8),

ψθθ=− being the true anomaly. The equation of the conic takes

the form

(

)

222

(1 cos ) / /re pbaacaaceψ+===−=−, where we used the

notations (9.1.2), (9.1.2''); if we take into account the above change of variable, then we

have

cos ( )/ coscr area uψ+=−=. The ordinate of the point

meets the

director circle of the ellipse at

Q ; if

uQOF= , then we notice that

cos cosOQ u a u= is given by cosOF FM c r ψ+=+ , hence just the expression

obtained above. The angle

u has thus a simple geometric interpretation and is called

eccentric anomaly. The Cartesian co-ordinates of the ellipse are easily obtained in the

form (with respect to the axes in Fig.9.7)

(cos )xa ue=−,

1sinxa e u=− ,

(9.2.14)

where we took into account the relations

(1 cos )ra e u=− , cos cosaucrψ

+ .

(9.2.14')

One gets also

cos

(1 cos )

auc

aeu

−

;

(9.2.14'')

observing that

Newtonian theory of universal attraction

565

1cos 1cos 1 1cos

1 cos 1 cos 1 1 cos

ac u e u

−+−+−

+−+−+

we obtain, finally, the relation which links the eccentric anomaly to the true anomaly in

the form

tan tan

21 2

ψ +

−

(9.2.15)

Considering the equation (9.2.9'), we may write (

0γ

≠

)

(

)

() ()

22 2

ηη

γγ

γη

γη γη

⎛⎞

=+−

⎜⎟

⎝⎠

∫∫ ∫

;

an integration by parts leads to

() ()

22 22 2 2

dddd

222

11 1 1

ηη ηη η η η

γη γη γη γη

γη γη

=+ =+ −

++ + +

∫∫ ∫∫

so that, finally, we have

(

)

()

22 2

11 11

ηη

γγ

γη γη

γη

⎛⎞ ⎛⎞

=− ++

⎜⎟ ⎜⎟

⎝⎠ ⎝⎠

∫∫

Thus, the equation (9.2.9') can be integrated in the form

322 2

11 1

() 1 1

(1 ) 1 1

ηη

γγ

γη γη

⎡

⎤

⎛⎞ ⎛⎞

−= − ++

⎜⎟ ⎜⎟

⎢

⎥

++ +

⎝⎠ ⎝⎠

⎣

⎦

∫

()

222

(1 ) 1 1 1

ηη

γη γη

⎛⎞

=−

⎜⎟

+− + +

⎝⎠

∫

(9.2.16)

We notice that

01e≤<

, so that

01γ

≤

; it results

()

arctan

γη

∫

By the change of variable

tan( / 2)uγη

, we find the equation

()

3/2

( ) ( sin ) (1 sin )

(1 ) 1

tt ue u e u

pee

−= − = −

+−

−

equivalent to Kepler’s equation (9.2.13).

MECHANICAL SYSTEMS, CLASSICAL MODELS

566

The particular case of circular motion (

) has been considered in the preceding

subsection; Kepler’s equation (9.2.13) puts thus in evidence a uniform motion.

2.1.4 Keplerian motion. Kepler’s laws

In the case in which the centre of attraction

S of mass M , considered to be fixed, is

the Sun, the particle in motion (with respect to the centre

S ) being a planet P , we

have to do with the solar system. Analogously, one may consider the motion of a

satellite of a planet with respect to that one, e.g., the motion of the Moon with respect to

the Earth. We are in the case of the elliptic motion, considered above. Kepler’s laws,

enounced in Subsec. 1.1.1 as a synthesis of astronomical observations, are obtained

now as a mathematical consequence of the Newtonian model of the considered

mechanical system. The results thus obtained allow us to state

Theorem 9.2.1 (Kepler, I). The motion of a planet around the Sun is an elliptic one, the

Sun being at one of the foci.

Theorem 9.2.2 (Kepler, II; the law of areas). In the motion of a planet around the Sun,

the radius vector of it describes equal areas in equal times.

In celestial mechanics, the notation

kfM

ma a

(9.2.17)

is used, so that Kepler’s equation may be written in the form

sin ( )ue u ntt

−

=−.

(9.2.13')

We notice that to a variation

2π of the true anomaly there corresponds the same

variation of the eccentric anomaly

u . Kepler’s equation (9.2.13') leads to the period T

in which the planet

P travels through the whole ellipse, hence effects a motion of

revolution (the radius vector describes the whole area of the ellipse) in the form

nfM

π==

;

(9.2.17')

it results that

n represents the circular frequency (called the mean motion too). We

may also write

(9.2.17'')

stating thus (the ratio

Mπ

depends only on the mass of the Sun)

Theorem 9.2.3 (Kepler, III). In the motion of planets around the Sun, the ratio of the

square of the revolution time to the cube of the semi-major axis is the same for all

planets.

The eccentricity

e of the orbits of the nine planets of the solar system (recently, a

tenth planet has been discovered) is, in general, very small as it results from the

Newtonian theory of universal attraction

567

mean

30 km/sv ≅ ). For the Moon, satellite of the Earth, we can make analogous

observations, the corresponding eccentricity being

0.066e

; the point of the orbit

which is the closest to the Earth is called perigee, while the point which is the most

distant is called apogee.

Table 9.1

Planet e

Mercury 0.2056 Mars 0.0933 Uranus 0.0471

Venus 0.0068 Jupiter 0.0484 Neptune 0.00855

Earth 0.0167 Saturn 0.0558 Pluto 0.2486

During the time, it was stated, by astronomical observations, with perfectionate

instruments, that the theorems enounced above correspond to the reality only with a

certain approximation. For instance, by the above calculation, one has obtained a

immobile perihelion, while the observations put into evidence a displacement of this

point of the planetary orbit, displacement which is more sensible for a planet close to

the Sun, which has a great eccentricity; especially, Mercury has a secular displacement

43.5'' of its perihelion, which has been put in evidence in 1859 by U.-J.-J. Leverrier.

To eliminate the non-correspondence between the theory and the observation, an

improvement of the mathematical model of Newtonian attraction law has been

attempted, by introducing an additional term or an exponent other than 2 at the

denominator; as well, it has been admitted the existence of a planet not discovered yet.

In this order of ideas, Weber modelled the phenomenon by introducing a non-

conservative force of universal attraction of the form

()

rrr

⎡⎤

=− +

⎢⎥

⎣⎦

FF, constc

(9.2.18)

but did not obtain satisfactory results concerning the deviation of Mercury’s perihelion.

Analogously, G. Armellini proposed a law of the form

[

]

rε=+FF, constε

, (9.2.18')

to may explain the existence of circular orbits. In both cases,

F is a force of Newtonian

attraction given by (9.1.7), (9.1.7'). But these non-concordances could be eliminated

only in the frame of a non-classical model of mechanics: the relativistic model.

Table 9.1, in which the planets are put in the order of the distances to the Sun. We

notice thus that, excepting Mercury and Pluto, the planets at the smallest and at the

greatest distance to the Sun, respectively, the other planets (the Earth included) have an

almost circular orbit; the closest to a circular is the orbit of Venus. The pericentre of the

orbit is called perihelion (denoted by

π ), while the apocentre is called aphelion

(denoted by

α ). Corresponding to the Theorem 9.2.2, a planet has the maximal velocity

at the perihelion and the minimal one at the aphelion; between those points the velocity

has a monotone variation. For instance, the Earth has the velocity

30.27 km/sv

the perihelion and the velocity

29.27 km/sv

at the aphelion (we take

MECHANICAL SYSTEMS, CLASSICAL MODELS

568

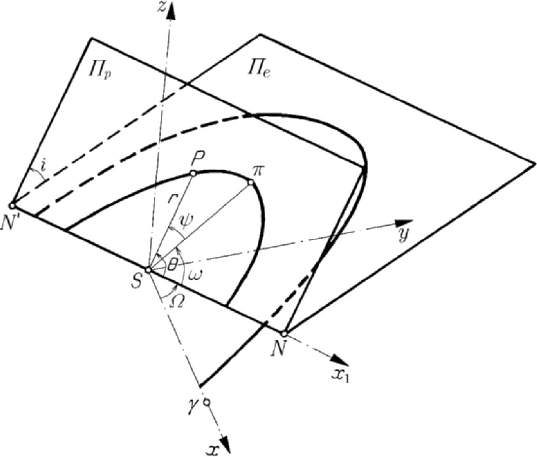
The elliptic motion of a planet is defined in space by six parameters, called the

elements of the elliptic motion. Using an ecliptic heliocentric frame, we take as

reference plane the ecliptic plane

Π (which contains the orbit of the Earth), denoted as

the

Sxy -plane (SF≡ ). The Sx -axis passes through the first point of Aries (the

vernal point)

γ (on the celestial sphere of radius equal to unity, at the intersection of a

plane parallel to the equatorial plane of the Earth, passing through the centre of mass of

the Sun, and the ecliptic plane), corresponding to the spring equinox, while the

Sy -axis

passes, e.g., through the point corresponding to the summer solstice; the

Sz -axis is

directed towards the boreal pole of the ecliptic. The plane

Π of the planet P orbit

intersects the ecliptic plane at the line of nodes

′

( N and N

′

are on the celestial

Figure 9.9. Elements of the elliptic motion of a planet.

sphere;

N is the ascending node from which z passes from negative values to positive

ones, while

′

is the descending node from which z passes from positive values to

negative ones); this plane is specified by the angle

SNγΩ

, called the longitude of

ascending node, and by its inclination

i with respect to the ecliptic plane (Fig.9.9).

Choosing

SN as

Sx -axis, we may specify the point π by

NSπωθ== (the

argument of perihelion); the angle

Ωω

(obtained by summing two angles in

different planes) is called the longitude of perihelion. The position of the ellipse is thus

given in its plane. The magnitude of the orbit is then put in evidence by the semi-major

axis

a and the eccentricity e . Finally, the motion along the ellipse is characterized by

the period

2/Tnπ= (the period of the revolution motion) and by the moment

= (the moment at which the planet P passes through the perihelion). Hence, the

Newtonian theory of universal attraction

569

elements of the elliptic motion are

,, , ,iaeΩω

and t

; these six elements may be

determined by measuring three directions from the Earth to the planet

P , from three

successive locations on the ecliptic.

We return now to Kepler’s equation (9.2.13'), written in the form

sinue u τ−=,

()nt tτ

− ,

(9.2.13'')

where

τ is the mean anomaly. The solution of this equation is of the form ()uuτ= ;

let us consider the function

()uττ

too. For

,uu

∈

, we may write

2121 21

() () (sin sin)uuuueuuττ−=−− − ; but

[

]

2 1 21 21 21 21

sin sin 2 sin ( )/ 2 2 ( )/ 2u u uu uu uu uu−≤ − ≤− =−=−

and

01e≤<, so that

() ()uuττ> . Hence, ()uτ is a continuous function on \ ;

the inverse function

()u τ exists and is uniform and continuous. Hence, there exists

only one continuous function

()uuτ

which verifies Kepler’s equation; in particular,

for

mτπ= it is seen that ()um mππ

, 0,1,2,...m

Let us consider the series expansions

sin ( ) sin

uamττ

∞

∑

cos ( ) cos

ub bmττ

∞

∑

with the Fourier coefficients

sin ( )sin d

aum

τττ

∫

cos ( )dbu

ττ

∫

cos ( )cos d

bum

τττ

∫

b being the mean value of cos ( )u τ on the interval

[

]

0, π . We notice that

sin ( )sin d sin ( )cos cos ( )cos dum um umu

ππ

τττ ττ ττ=− +

∫∫

[]

cos( ) cos( ) d

um um u

ττ=++−

∫

[][]

{}

cos ( 1) sin cos ( 1) sin d

mumeu mumeuu

=+−+−−

∫

[]

() ()

JmeJme

+−

cos ( )cos d cos ( )sin sin ( )sin dum um umu

ππ

τττ ττ ττ=+

∫∫

[]

() ()

JmeJme

−+

=−,

MECHANICAL SYSTEMS, CLASSICAL MODELS

570

[]

cos ( )d cos ( ) 1 cos ( ) duueuu

ππ

ττ τ τ=−

∫∫

(

)

sin sin 2

22 2

uu u e

=−+ =−

where we took into account Kepler’s equation (9.2.13'') and have introduced Bessel’s

functions of order

m defined in the form

( ) cos( sin )d

Jx mux uu

=−

∫

;

(9.2.19)

using the recurrence relations

[

]

2() () ()

mJ x x J x J x

−+

=+,

2() () ()

Jx J x J x

−+

=−,

(9.2.19')

we may, finally, write

sin ( ) ( )sin

uJmem

ττ

∞

∑

cos ( ) 2 ( )cos

uJmem

ττ

∞

=− +

∑

(9.2.20)

The relations (9.2.14') and (9.2.13'') lead to

11d

() 1 2 ( )cos

reJmem

ττ

∞

=+ −

∑

(9.2.21)

() 2 ( )sin

uJmem

ττ τ

∞

∑

(9.2.21')

Introducing the notation

−−

==<

+−

(9.2.22)

and observing that Euler’s formula

ecosisin

ϕϕ

=± leads to tan ϕ

(

)

(

)

2i 2i

i1 e /1 e

ϕϕ

=− + , we may write the relation (9.2.15) in the form

tan tan

ψλ

−

(9.2.15')

wherefrom

−

;

(9.2.15'')

Newtonian theory of universal attraction

571

applying now the logarithmic operator and taking into account the series expansion

ln(1 )

∞

−=−

∑

, 01x

≤

< ,

and Euler’s formula, we get, finally,

() () 2 sin ()

umu

ψτ τ τ

∞

∑

(9.2.22')

We have thus put in evidence the polar co-ordinates

()rrt

and ()tψψ= of the

planet

P in the plane of the orbit, as well as the eccentric anomaly ()uut= (solution

of Kepler’s equation) as function of the time

/tt nτ

+ .

2.1.5 Hyperbolic motion

The trajectory of the particle acted upon by a Newtonian force of attraction is a

hyperbola if

0h > (we may have 0k > , e.g., kfmM

, or 0k

, when we have

only

0h > ); in the hyperbolic motion, the equation (9.2.5') takes the form (we have

1e > )

(

)

1ex−

2xpex p−− =−. The equation reads

()

xae

−

(9.2.23)

too, where we have introduced the semiaxes (Fig.9.10)

−

(9.2.23')

and the focal distance

pe k e

cea a b

== = = +

−

;

(9.2.23'')

we notice that, for a given potential (

k is given), the semi-major axis of the hyperbola

depends only on the mechanical energy constant

h . The semiaxes of the hyperbola may

be expressed with the aid of the initial conditions in the form

⎛⎞

−

⎜⎟

⎝⎠

sin

−

;

(9.2.23''')

as in case of the elliptic motion,

a does not depend on the direction of the initial

velocity. The inclinations of the asymptotes are

/12/ba e C mh k±=±−=± . In