Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics
Подождите немного. Документ загружается.


MECHANICAL SYSTEMS, CLASSICAL MODELS
592
2
1
21
1
mC n h
e
π
⎛⎞
′
=−=
⎜⎟
⎝⎠
−
;
as well
22
00
dd2pmCmCnh
ππ
θ
ϕψπ===
∫∫
.
Finally, we get
mC n= = ,
2
2
2
1
()
n
e
nn
=−
′
+
, ,nn
′
∈
` ,
(9.2.60)
where
34
1.0545919 10 J s
2
h
π
−
== ⋅ ⋅=
(9.2.61)
is the rationalized Planck’s constant (in the SI-system, in joule-seconds). The first
relation (9.2.60) determines the magnitude of the ellipse, because (see the relations
(9.2.7) and (9.2.12') too)
() ()()
22
2222
22 22 2 2 2
0000
()
1/1 1
nn
CmCn
a
ee m ee eme me
′
+
====
−−−
=
=
,
(9.2.62)
while the second relation (9.2.60) specifies its form.
Taking into account (9.2.58) and (9.2.59), the kinetic energy is given by
()
2
2
2
222 2
22
11d
1
22 d
2
r
p
mmCr
Trr p
mr
rr
θ
θ
ψ
⎡
⎤
⎛⎞
⎛⎞
=+= += +
⎜⎟
⎜⎟
⎢
⎥
⎝⎠
⎝⎠
⎣
⎦
()
22
2
22
1
cos
2
1
mC e
e
ae
ψ
+
⎛⎞
=+
⎜⎟
⎝⎠
−
,
while the potential energy reads
()
22
00
2
(1 cos )
1
ee
Ve
r
ae
ψ=− =− +
−
;
the mechanical energy results in the form
() ()()
22 2
22
00
22 22
11 cos
2
11 11
mC e e mC
ETV e e
a
ae e aeae
ψ
⎡
⎤
+
⎛⎞
=+= − + −
⎢
⎥
⎜⎟
−− −−
⎝⎠
⎣
⎦
,
so that, taking into account (9.2.62), we get

Newtonian theory of universal attraction
593
24
00
2
1
22
()
eme
E
a
nn
=− =−
′
+
=
.
(9.2.63)
From this basic formula in the theory of lines spectra, we see that on a stationary
trajectory with the quantic numbers
n and n
′
the mechanical energy is constant.
Considering two stationary trajectories of indices 1 and 2, the principle iii) shows
that the emitted energy has a frequency given by
21
hEEν =− (if
22 11
nn nn
′′
+>+, then
21
EE> ); we obtain Ritz’s law
22
11 22
11
()( )
R
nn nn
ν
⎡
⎤
=− −
⎢
⎥
′′
++
⎣
⎦
,
(9.2.64)
where
4
0
3
4
me
R
π
=
=
(9.2.64')
is Rydberg’s constant.
We notice that the quantic numbers appear only in the combination
nn
′
+ , so that
we may consider that we have only one quantic number, called principal quantic
number (as only one degree of freedom would be quantified). The relation (9.2.64)
emphasizes the lines spectrum of the hydrogen, with the various series obtained on an
experimental way (Balmer, Fowler etc.).
Chapter 10
OTHER CONSIDERATIONS ON PARTICLE
DYNAMICS
To complete the study of a mechanical system, which can be modelled by only one
particle, we present some problems with a special character; we consider thus the
motion with discontinuity, the motion of the particle with respect to a non-inertial frame
of reference, as well as the motion of the particle of variable mass.
1. Motion with discontinuity
In the mathematical modelling of the motion of a particle we assumed, in general,
that the vector
r has derivatives of the first and the second order (its components are
functions of class
2
C ); as well, we assumed that the force (,;)t
=
FFrr is continuous
with respect to the position vector, the velocity and the time. In this case, we have seen
that the equations of the problems that are put may be integrated with certain boundary
conditions and in certain conditions of existence and uniqueness.
But, in case of many mechanical phenomena, the conditions of continuity mentioned
above are not fulfilled; such phenomena cannot be easily integrated in the classical
schemata based on usual functions. There appears thus the necessity to extend
Newtonian mechanics and to complete its mathematical model with the aid of the
methods of the theory of distributions. We establish thus the general equation of motion
with discontinuity of a particle, stating then the general theorems corresponding to this
motion.
1.1 Particle dynamics
After some general considerations concerning the trajectory, the velocity, the
acceleration and the force, we establish, in what follows, the fundamental equation of
motion for a free particle, as well as for a particle subjected to constraints. A special
attention is paid for the motion of the heavy particle in vacuum.
1.1.1 General considerations
One of the mechanical phenomena which needs the introduction of methods of the
theory of distributions is (as it was seen in Chap. 5, Subsec. 1.2.6) that in which the
position vector is a continuous function, while the velocity and the acceleration have
discontinuities of the first species at
0
tt
=
, i.e.
00
(0)(0)tt
−
≠+vv and
00
(0)(0)tt−≠ +
vv.
595
MECHANICAL SYSTEMS, CLASSICAL MODELS
596
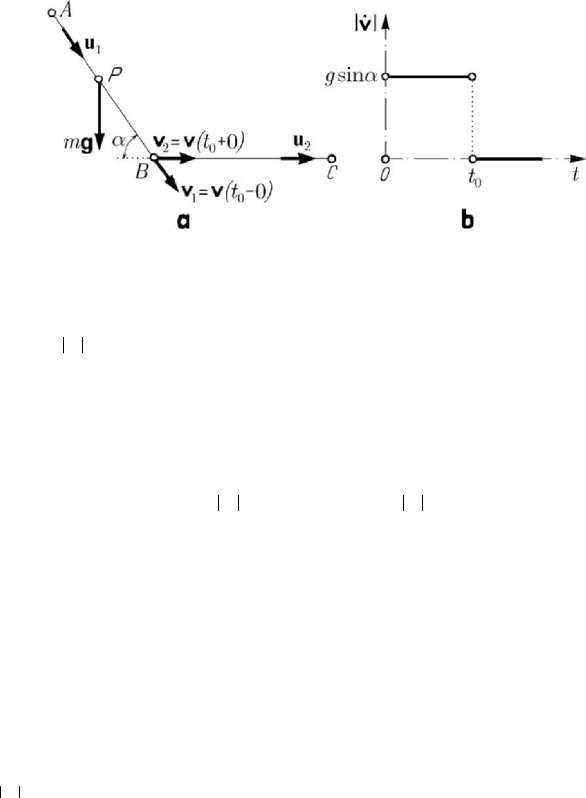
A simple example of such a mechanical phenomenon is the motion of a heavy
particle
P on a trajectory ABC (a broken line, Fig.10.1,a), assuming, for the sake of
simplicity, that it is frictionless; in fact, the character of the mechanical phenomenon
does not change if the friction is taken into consideration. As it is easy to see, the
trajectory of the particle
P is represented by a continuous function, formed by two
segments of a line
AB and BC ; we notice that the function which represents the
trajectory has not derivatives of first and second order at
B , so that we cannot
determine the velocity, the acceleration and the constraint force at this point. We
assume that at the moment
0t
=
the particle is at A and that at the moment
0
tt= it
reaches
B ; in this case, the acceleration modulus may be written in the form
Figure 10.1. Particle in motion on a broken line. Trajectory (a);
the acceleration modulus vs time (b).
[]
0
0
0
sin for 0 ,
sin 1 ( )
0 for ,
gtt
gtt
tt
α
αθ
≤
<
⎧
⎪
=−−=
⎨
>
⎪
⎩
v
(10.1.1)
where
g is the gravity acceleration (Fig.10.1,b), while θ is Heaviside’s function. A
discontinuity of the first species is thus put into evidence, because, at the moment
0
tt= , we may write
0
0
lim sin
tt
g α
→−
=
v
,
0
0
lim 0
tt→+
=
v
.
We notice also that, besides the discontinuity of the modulus, the acceleration has also a
discontinuity in direction; thus, the acceleration vector has a discontinuity of the first
species at the moment
0
tt= , given by
0
11
0
lim ( ) sin
tt
tgα
→−
=
=
va u
,
0
0
lim ( )
tt
t
→+
=
v0
, (10.1.1')
where the unit vector
1
u specifies the line AB and is directed corresponding to the
motion of the particle. The modulus of the velocity reads, in this case,
[]
0
00
00
sin for 0 ,
sin ( ) ( )
sin for ,
gt t t
gttkttt
kgt t t
α
αθ
α
≤
<
⎧
⎪
=−−−=
⎨
>
⎪
⎩
v
(10.1.2)

Other considerations on particle dynamics
597
where
k , 01k≤≤, is a coefficient of restitution. Corresponding to the principle of
inertia, the velocity of the particle on
BC must be equal to the velocity at the right of
B , hence equal to
0
(0)t +v . But this velocity is not known, so that it remains non-
determinate on
BC . To solve the problem, we assume that at the point of discontinuity
takes place a phenomenon of collision; hence, we assume that the magnitude of the
velocity at the right is proportional to its magnitude at the left, that is
00
(0) (0)tkt
+
=−vv. (10.1.3)
If the coefficient of restitution is equal to unity (
1k
=
), then the collision at B is
perfect elastic and the magnitude of the velocity is a continuous function. Usually, this
is the hypothesis that is assumed, although it is not the only possibility. Indeed,
independent of the modulus of the velocity on the segment of a line
BC , specified by
the unit vector
2
u , directed corresponding to the motion, the velocity vector has a
discontinuity of the first species at
B , because
0
00
11
0
lim ( ) ( 0) ( 0)
tt
tt vt
→−
=
−= − =vv uv
,
0
00
22
0
lim ( ) ( 0) ( 0)
tt
tt vt
→+
=
+= + =vv uv
;
(10.1.4)
Figure 10.2. The collision model for a particle in motion on a broken line.
The velocity modulus vs time.
1
v is the velocity of the particle P at B on AB , while
2
v is the velocity of the same
particle at
B on BC . In Fig.10.2 is drawn the diagram of the modulus of the velocity
as a function of time (the line segments
ON and NQ for 1k
=
, the line segments
ON and NQ
′′
for 01k<< and the segments ON and NQ
′
′′′
for 0k = , the case
of a plastic collision).
The study of problems of the kind considered above needs the introduction of
various mechanical quantities in the frame of the theory of distributions.
1.1.2 Trajectory. Velocity. Acceleration. Force. Principles of mechanics
Starting from the equation
()t
=
rr of the trajectory, we introduce the velocity
() ()tt=
vr and the acceleration () () ()ttt
=
=
avr as continuous functions of t in
the interval
[
]
,tt
′′′
, excepting a finite number of discontinuities of the first species at
MECHANICAL SYSTEMS, CLASSICAL MODELS
598
the moments
i
tt= ,
i
ttt
′′′
<<
,
1,2,...,in
=
. In these conditions, the jump
i
V of
the velocity, given by (5.1.34'), allows to introduce the complementary acceleration
()
c
ta in the form (5.1.34''); adding the acceleration in the usual sense ()t
a to this
acceleration, we obtain the acceleration in the sense of the theory of distributions
()ta
(the formula (5.1.34''')), corresponding to the Theorem 5.1.2 of the generalized
acceleration.
Taking into account Newton’s law (1.1.89), we introduce the notations
() ()tmt=Fa,
() ()tmt=
Fa
, () ()
cc
tmt
=
Fa, (10.1.5)
where
()tF is the generalized force (in the sense of the theory of distributions),
()tF
is the force in the usual sense, while ()
c
tF is the complementary force due to the
discontinuities; the relation (5.1.34''') becomes
() () ()
c
tt t=+FFF. (10.1.5')
We thus state
Theorem 10.1.1 (theorem of the generalized force). The generalized force (in the sense
of the theory of distributions), which acts upon a particle, is equal to the sum of the
force in the usual sense and the complementary force (due to discontinuities), which act
upon the same particle.
In this case, one can affirm that by introducing the generalized accelerations and
forces, as well as by using the derivatives in the sense of the theory of distributions, the
second principle of mechanics, given by the formula (1.1.89), may be used in the frame
of this theory too.
In what concerns the principle of inertia, we assume that for the generalized force
=F0 we have =a0, that is
1
() ( )
n
ii
i
ttt
=
+
−=
∑
aV 0
. (10.1.6)
Considering the arbitrary fundamental function
()tϕ , the support of which does not
contain the moments
i
t , 1,2,...,in
=
, the relation (10.1.6) leads to
(
)
(), ()ttϕ =
a0,
wherefrom we deduce that the function
()t
a vanishes everywhere, excepting
eventually at the moments
i
t . Let be now a fundamental function ()tϕ , the support of
which contains only the moment
i
t ; we obtain ()
ii
tϕ
=
V0, so that
i
=V0.
Proceeding in the same manner for
1,2,...,in
=
, we may write
i
=V0,
1,2,...,in= , ; replacing in (10.1.6), it results ()t
=
a0, hence the particle has a
rectilinear and uniform motion. In conclusion, the principle of inertia (which represents
a criterion by which we may know if upon a particle is acting a force) can be enounced
in the classical form.
The other three principles of mechanics may be applied as in the case of the classical
model.
Other considerations on particle dynamics
599
1.1.3 Basic equation of motion
The motion of a particle is modelled by the second principle of Newton. We consider
thus the equation of motion (6.1.22), where
()tF is the generalized force (10.1.5') and
the differentiation takes place in the sense of the theory of distributions; we assume that
()tr is defined for t ∈ . This represents one of the methods to express the equation
of motion in distributions; the boundary conditions must be separately specified.
If we wish to include the boundary conditions in the equation of motion, then we use
another procedure. We start from the same equation of motion (6.1.22), but the force is
that in the usual sense
F ; differentiating in the usual sense too, we write
2
2
d
() ()
d
mtt
t
=
rF
,
0
tt> . (10.1.7)
We assume that, at the initial moment
0
tt
=
, the position vector and the velocity are
given by
0
r and
0
v , respectively (initial conditions of Cauchy type). We introduce a
new function
()rt , defined for
t
∈
by the relation
0
00 0
0
for ,
() ( )() for ,
() for ;
tt
tttt tt
ttt
θ
⎧
<
⎪
⎪
=− = =
⎨
⎪
>
⎪
⎩
0
rrr
r
(10.1.8)
the velocity reads
0
00 0
0
for ,
() ( ) () for ,
() for .
tt
tttt tt
ttt
θ
⎧
<
⎪
⎪
=− = =
⎨
⎪
>
⎪
⎩
0
vvv
v
(10.1.8')
We notice thus that
0
r and
0
v are the jumps of the position vector and of the velocity,
respectively, at the initial moment
0
tt
=
. Differentiating successively the distribution
corresponding to the function (10.1.8), we get the velocity and the acceleration of the
particle in the form
00
dd
() () () ( )
dd
ttttt
tt
δ==+−
vrrr ,
2
2
0000
22
dd
() () () ( ) ( )
dd
ttttttt
tt
δδ==+−+−
arrv r
.
The first of these relations corresponds to the distribution defined by (10.1.8'); as well,
the velocity and the acceleration in the usual sense have been put into evidence.
Replacing in the equation (10.1.7) and assuming that, besides the moment of
MECHANICAL SYSTEMS, CLASSICAL MODELS
600
discontinuity
0
tt= , may appear also other moments of discontinuity, which introduce
the complementary force
()
c
tF , we can write the basic equation of mechanics in the
form
2
0000
2
d
() () ( ) ( )
d
mttmttmtt
t
δδ=+ −+ −
rF v r
, (10.1.9)
where the generalized force
()tF is given by (10.1.5), (10.1.5').
By means of the formula (A.3.33'), we may write a fundamental particular solution
of the operator
22
d/dt in the form
() ()Et t t tθ
+
=
= ; (10.1.10)
in this case, the solution of the equation (10.1.9) is given by
0000
1
() () () ( ) ( )t tt t tt tt
m
θδδ
⎡
⎤
=∗ + −+−
⎢
⎥
⎣
⎦
rFvr
,
wherefrom it results
00 0 0
1
() () ( ) ( )ttt tt tt
m
θ
++
=∗+−+ −rFvr
. (10.1.11)
If
()tF is a locally integrable function, then we may write
00 0
0
1
() ( ) ( )d ( )
t
tt tt
m
τττ=− +−+
∫
rFvr
,
0
tt≥ . (10.1.11')
In particular, if
0
() constt ==
FF ,
c
=
F0, then we get
2
00 00 00
1
() () () ()
2
ttt tt tt
m
θ
++
=− +− +−rFvr; (10.1.12)
this relation may be expressed also in the form
2
00 000
1
() ( ) ( )
2
ttt tt
m
=− +−+rFvr
,
0
tt≥ . (10.1.12')
In the case in which
(,;)t=
FFrr, the basic equation remains, further, of the form
(10.1.9), the force in the sense of the theory of distributions having, obviously, this
general character. To solve this equation one can no more use the method given above,
because one must take into account the new form of the differential equation of motion.

Other considerations on particle dynamics
601
1.1.4 Case of a particle subjected to constraints
In case of a particle subjected to constraints, these ones must be eliminated by
introducing constraint forces. Let us thus consider the case of a particle subjected to a
single holonomic and rheonomic bilateral constraint (the case of two constraints may be
studied analogously), expressed in the form
123
(, , ;) 0
f
xxxt
=
, where the function
f
is piecewise defined in the form
123 123
1
(, , ;) (, , ;)
n
i
i
f
xxxt f xxxt
=
=
∑
; (10.1.13)
we denoted
123 1
123
1
( , , ; ) for ( , ),
(, , ;)
0 for ( , ),
ii
i
i
i
i
f
xxxt t t t
fxxxt
ttt
−
−
∈
⎧
⎪
=
⎨
∉
⎪
⎩
(10.1.13')
assuming that
0
12 1
...
n
n
ttt t t
−
<<<< < for the moments of discontinuity.
Eliminating the constraint and introducing the generalized constraint force
()tR ,
the equation of motion of the particle, considered now as a free one, reads
2
2
d()
() ()
d
t
mtt
t
=+
r
FR
, (10.1.14)
where, for the sake of simplicity, in the generalized force
()tF we have introduced also
the sum
0000
() ()mttmttδδ−+ −
vr, which is of the nature of a complementary
force.
The generalized constraint force
()tR may be expressed by the relation
1
() ()
n
i
i
tt
=
=
∑
RR
, (10.1.15)
where
()
i
tR are the generalized constraint forces given by
() () ()
i
iic
tt t=+RRR. (10.1.15')
We denoted by
()
i
tR the constraint forces in the usual sense, which correspond to the
moments
1
(,)
i
i
ttt
−
∈
, 1,2,...,in= , and are expressed in the form
() () ()grad
i
ii
ii
ttf tfλλ==R ∇ , (10.1.15'')
where
()
i
tλ is a scalar, ∇ is Hamilton’s operator and
1
i
f
C∈ ; as well, ()
ic
tR are
complementary constraint forces, corresponding to the moments of discontinuity
i
t ,

MECHANICAL SYSTEMS, CLASSICAL MODELS
602
0,1,2,...,in=
. The constraint forces in the usual sense are directed, in the intervals of
definition, along the normals to the surfaces
123
(, , ;) 0
i
f
xxxt
=
, considered as rigid at
the moment
1
(,)
i
i
ttt
−
∈ . On the intersection lines of these surfaces, that is on the lines
corresponding to the moments
i
t , these forces cannot be determined by means of the
expressions (10.1.15'').
To obtain a unitary expression of the generalized constraint force
()
i
tR , we use the
equation of motion (10.1.14), written in the form
2
2
d
() () ()
d
tttm
t
≡+− =
r
FR 0F ; (10.1.14')
this equation may be written everywhere, excepting the points which correspond to the
moments
i
t . We introduce also the moments of discontinuity if we replace the equation
(10.1.14') by the equation
1
1
()()
i
n
m
i
i
tt t
+
=
−
=
∏
F 0
,
i
m
∈
, (10.1.14'')
which, obviously, may be written for
t
∈
. In the frame of the usual functions, the
solution of the equation (10.1.14'') is (10.1.14'); to obtain a generalized solution, we
assume that
()tF can be a distribution and we consider the equation (10.1.14'') in the
sense of the theory of distributions. Thus, the solution in distributions of the equation
(10.1.14'') includes, as a particular case, the solution (10.1.14') too.
To can make a study of the equation (10.1.14''), there are necessary some results
concerning the structure of the distributions with punctual support. In this order of
ideas, we state
Theorem 10.1.2. A distribution ()
f
x of a single variable satisfies the equation
()() 0Pxfx
=
, (10.1.16)
where
()Px is a polynomial, if and only if that one is expressed in the form
1
()
110
() ( ) ( )
k
m
sr
kj
ii j
k
ikj
f
xcxx cxxδδ
−
===
′
=−+ −
∑∑∑
. (10.1.16')
Here,
i
x , 1,2,...,is= , are the simple roots of the polynomial ()Px , while
k
x
′
,
1,2,...,kr= , represent the multiple roots, the multiplicity order of which is
k
m ; the
quantities
i
c and
k
j
c are constants, while δ is Dirac’s distribution.
As well, we can state
Theorem 10.1.3. If the support of the distribution ()
f
x is formed by the points
i
x ,
1,2,...,in= , then ()
f
x is of the form
