Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics
Подождите немного. Документ загружается.


Other considerations on particle dynamics
613
Let
′
v and
′′
v be the velocities of the particle before and after collision,
respectively; we can write the theorem of momentum (10.1.41) in the form
0
()mm
′
′′
=
−=vvvP. (10.1.43)
A scalar product of this relation by
′
′
v leads to
2
()mv m
′
′ ′ ′′ ′′
−
⋅=⋅vv Pv or
0
TTT
′′ ′ ′′
−+=⋅Pv, where (
0
′
′′
=
−vvv)
2
1
()
2
Tmv
′′
=
,
2
1
()
2
Tmv
′′ ′′
=
,
22
00
11
()
22
Tm mv
′′ ′
=−=
vv (10.1.44)
are the kinetic energy before and after collision and the kinetic energy of the lost
velocities, respectively. The variation of the kinetic energy is given by
0
()TTT
′
′′
Δ
=−; (10.1.44')
thus, we may write
00
()TT
′
′
Δ
+=⋅Pv (10.1.45)
and we can state
Theorem 10.1.13 (theorem of kinetic energy). The sum of the variation of the kinetic
energy of a free particle at a moment of discontinuity and the kinetic energy of the lost
velocity at the same moment is equal to the scalar product of the percussion which acts
upon the particle by the velocity after that moment of discontinuity.
If the relation
0
′
′
⋅
=Pv (10.1.46)
takes place, which can happen, e.g., if the velocity of the particle vanishes after
collision, then we obtain the relation
00
() 0TT
Δ
+=, (10.1.47)
so that we may state
Theorem 10.1.14 (Carnot). If, in the motion of a free particle subjected to collision, the
condition (10.1.46) is fulfilled, then the sum of the variation of the kinetic energy of that
particle at a moment of discontinuity and the kinetic energy of the lost velocity at the
same moment is equal to zero.
A scalar product of the relation (10.1.43) by
′
v leads to
2
()mmv
′
′′ ′ ′
⋅
−=⋅vv Pv
or to
0
TTT
′′ ′ ′
−−=⋅Pv, wherefrom
00
()TT
′
Δ
−=⋅Pv; (10.1.45')
we may thus state

MECHANICAL SYSTEMS, CLASSICAL MODELS
614
Theorem 10.1.13' (analogous to the theorem of kinetic energy). The difference between
the variation of the kinetic energy of a free particle at a moment of discontinuity and
the kinetic energy of the lost velocity at the same moment is equal to the scalar product
of the percussion which acts upon this particle by its velocity before that moment of
discontinuity.
If, in particular,
0
′
⋅
=Pv , (10.1.46')
it results
00
()TT
Δ
= . (10.1.47')
Thus, we state
Theorem 10.1.14' (analogous to Carnot’s theorem). If the condition (10.1.46') is
fulfilled, in the motion of a free particle subjected to collision, then the variation of the
kinetic energy of that particle, at a moment of discontinuity, is equal to the kinetic
energy of the lost velocity at the same moment.
Summing the relations (10.1.45) and (10.1.45'), we get
0
1
() ( )
2
T
′
′′
Δ=⋅+
Pv v, (10.1.48)
so that it results
Theorem 10.1.15 (Kelvin). The variation of the kinetic energy of a free particle at a
moment of discontinuity is equal to the scalar product of the percussion which acts
upon the particle by the semi-sum of both the velocities before and after the
phenomenon of discontinuity.
Subtracting (10.1.45') from (10.1.45), we get
00
11
()
22
T
′′ ′
=⋅−=⋅
Pv v Pv
; (10.1.48')
we may thus write
Theorem 10.1.15' (analogous of Kelvin’s theorem). The kinetic energy of the lost
velocity of a free particle at a moment of discontinuity is equal to half of the scalar
product of the percussion which acts upon the particle by the jump of the velocity at the
moment of discontinuity.
The phenomenon of collision will be studied in detail in Chap. 13, §1, where the
corresponding mathematical model is better put in evidence in case of a mechanical
system which is not reduced to only one particle.
Other considerations on particle dynamics
615
2. Motion of a particle with respect to a non-inertial frame of
reference
The results obtained till now concerning the motion of a particle are using the
fundamental law of Newton, written with respect to an inertial frame of reference.
Taking into account that not all frames are inertial (or cannot be approximated to
inertial ones), it is necessary to perform a study of the motion of a particle with respect
to a non-inertial frame (starting, e.g., from a geocentric or heliocentric frame); we
obtain thus important results concerning terrestrial mechanics too.
2.1 Relative motion. Relative equilibrium
Starting from the results obtained in Chap. 5, Sec. 3.1, concerning kinematics of the
relative motion of a particle, we make, in what follows, a study of dynamics of the
relative motion of that particle; in particular, we get results for the relative equilibrium
of it. The application of general theorems leads to the law of motion with respect to a
movable frame; one can thus specify the set of inertial frames which forms the Galileo-
Newton group. As well, we put in evidence the general theorems and conservation
theorems of mechanics and the principle of equivalence.
2.1.1 Dynamics of the relative motion of a particle
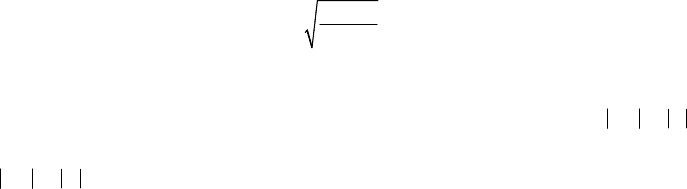
Let be an inertial frame of reference
123
Ox x x
′
′′′
, which is considered to be fixed, and
a non-inertial frame (movable frame)
123
Ox x x
in motion with respect to the fixed one.
Newton’s law (1.1.89) for a particle
P
is written with respect to an inertial frame (in
absolute motion); in Chap. 5, Sec. 3.1 we have seen that the absolute motion is obtained
by the composition of the relative motion and the transportation one (a vector
composition for the velocities, while for the accelerations one must add the Coriolis
acceleration too). Starting from the formula (5.3.5) of composition of the accelerations
and multiplying both members by the mass
m , we can write
ar
t
C
mmmm=++aaaa, where ,,
r
t
C
aaa are the transportation, relative and
Coriolis accelerations, respectively, given by (5.3.4). Taking into account the equation
of motion of a free particle (
a
m
=
aF, where
F
is the resultant of the given forces),
we get
r
t
C
m
=
++aFFF, (10.2.1)
where
[
]
()
tt
O
mm
′
=− =− + × + × ×
Fa a r r
ω
ωω ,
2
r
CC
mm
=
−=−×Fa v
ω
(10.2.1')
are complementary forces (the transportation force and the Coriolis force,
respectively); these forces are added to the given force
F and allow writing the
equation of motion in a non-inertial frame of reference. We notice that the forces
t
F
and
C
F depend on
O
′
a and
ω
, hence on the acceleration of the movable frame pole and
MECHANICAL SYSTEMS, CLASSICAL MODELS
616
on the rotation vector of this frame with respect to the fixed (inertial) one, respectively;
hence, the motion with respect to a non-inertial frame can be determined only starting
from an inertial one.
The complementary forces are called also inertial forces because their magnitude is
proportional to the inertial mass; these forces are applied to the particle in motion
(unlike the forces of inertia (6.2.11) which are applied to the agent which provokes the
motion). The inertial forces are real ones with respect to an observer linked to a non-
inertial frame of reference; e.g., the centrifugal force, which appears in a motion of
rotation, is a transportation force.
Introducing the relative force
r
t
C
=
++FFFF, (10.2.2)
we may write the equation (10.2.1) in the form
rr
m
=
aF, (, ;)
rrr
t
=
FFrv ; (10.2.2')
we put initial conditions of Cauchy type
00
()t
=
rr,
0
0
()
rr
t =vv (10.2.2'')
and notice that one can use all the results given in Chap. 6, stating thus
Theorem 10.2.1 (theorem of the relative motion). The equation of motion of a particle
with respect to an inertial frame of reference maintains its form with respect to a non-
inertial one if the given force is replaced by the force relative to the latter frame.
As well, we state
Theorem 10.2.2 (theorem of the relative force). The relative force (with respect to a
non-inertial frame of reference) is equal to the sum of the given force and the
complementary forces (the force of transportation and the Coriolis force) with respect
to an inertial one.
In case of a particle subjected to bilateral constraints, we use the axiom of liberation
of constraints, introducing the constraint force
R . The equation of motion (10.2.1)
becomes
r
t
C
m
=
++ +aFFFR; (10.2.1'')
taking into account (10.2.2), we may also write
rr
m
=
+aFR (10.2.2''')
too. We notice that the Theorems 10.2.1 and 10.2.2 remain still valid.
Thus, the problem of motion with respect to a non-inertial frame of reference may be
reduced to a corresponding problem with respect to an inertial frame, chosen
conveniently (with respect to which the Newtonian model of mechanics is verified with
a sufficient good approximation).
Other considerations on particle dynamics
617
2.1.2 Particular cases of non-inertial frames of reference
Let us consider first of all the case of a non-inertial frame of reference in a motion of
translation with respect to an inertial one; hence, we assume that
=
0
ω
. In this case,
the equation of motion is (
t
O
m
′
=
−Fa,
C
=
F0)
r
O
mm
′
=
−aF a. (10.2.3)
We assume, in particular, that the particle
P is acted upon by its own weight
(
m=Fg), so that we can write
r
O
′
=
−aga. (10.2.4)
In the case in which
O
′
ag we have the elevator problem. If
O
′
a has the same
direction as
g (it is directed towards the centre of the Earth), then the particle P seems
to be lighter (
r
O
′
=−aga), while if
O
′
a has a direction opposite to that of g
(
r
O
′
=+
aga), then the particle seems to be heavier. In particular, if the elevator is in a
free falling (
O
′
=
ag), then the apparent weight of the particle with respect to it
vanishes; we are in the case of imponderability.
Moreover, let us suppose that
const
O
′
=
a . If, for instance, the particle is in free
falling (
0
0v = for 0t = ) from a height h with respect to the floor of the elevator
(
0x = , the Ox -axis of unit vector i along the ascendent vertical), we get, in the
movable non-inertial frame,
()
2
/2
O
xgat h
′
=
−+ +, so that the falling time is given
by
2
O
h
T
ga
=
′
+
, (10.2.5)
assuming that
0
O
ga
′
+> (
OO
a
′
′
=
ai, with 0
O
a
′
> , of an opposite direction to that of
the gravitation
g=−gi, or with 0
O
a
′
<
, of the same direction but with
O
′
<
ag).
If
0
O
ga
′
+=, then the particle is immobile, while if 0
O
ga
′
+
< ( 0
O
a
′
< with
O
′
>
ag), then the particle goes up along the vertical Ox with respect to an observer
linked to the movable frame. If
0
O
a
′
=
, then the movable frame becomes an inertial
one, finding again the usual laws of falling.
Another important particular case is that of a non-inertial frame of reference in
motion of rotation with respect to a fixed
3
Ox
′
-axis (
OO
′
′
=
=va0,
3
ω= iω ,
()tωω= , Fig.10.4). The transportation force is given by ( OP P P
′′
=+
r
0
OP
′
=+
r )
00
() ( )
t
mm m m=− × − × × =− × − × ×
Fr rr rωωω ω ωω
020
3
mmωω=− × +
ir r
,
(10.2.6)
MECHANICAL SYSTEMS, CLASSICAL MODELS
618
corresponding to Rival’s formula (5.2.6'''), and the Coriolis force by
3
22
rr
C
mmω=− × =− ×Fviv
ω
. (10.2.6')
In case of a uniform rotation (
=
0
ω
), we have
20
t
mω=Fr
. (10.2.6'')
Figure 10.4. Non-inertial frame of reference in motion of rotation with respect to a fixed axis.
Assuming that the particle
P is moving in the
13
Ox x -plane (with respect to the non-
inertial frame) and taking into account (10.2.6), (10.2.6'), we may write the equation of
motion (10.2.1) in components, in the form
2
11 1
mx F m xω=+
,
21 1
02Fmx mxωω
=
−−
,
33
mx F
=
;
observing then that
ωθ=
and replacing
1
x by r and
3
x by z , we find again the
equations of motion of the particle in cylindrical co-ordinates (6.1.26), with respect to a
fixed (inertial) frame.
By composition of the two particular cases considered above, one can obtain the case
of a non-inertial frame of reference in a finite motion of rototranslation with respect to
an inertial one. In the case of a non-inertial frame of reference in an arbitrary motion
with respect to an inertial one, one may use the results obtained in Chap. 5, Subsec.
2.3.1 concerning the instantaneous helical motion.
If the forces do not intervene explicitly in the relative motion, then the composition
of motions can be reduced to the composition of velocities. Let be thus the case of a
non-inertial frame in motion of translation with respect to an inertial one, with the
velocity
O
′
v ; if the particle has a relative velocity
r
v , then the composition of the
velocities leads to
r
O
′′
=+
vv v. Assuming that the velocities
O
′
v and
r
v are collinear
(e.g., a boat which is moving with the velocity
r
v along a river, the velocity of
which with respect to the riversides is
O
v
′
), we have
r
O
vv v
′
′
=
+ (the boat is moving
Other considerations on particle dynamics
619
in the same direction as the river) or
r
O
vvv
′
′
=
− (the boat is moving in a direction
opposite to that of the river).
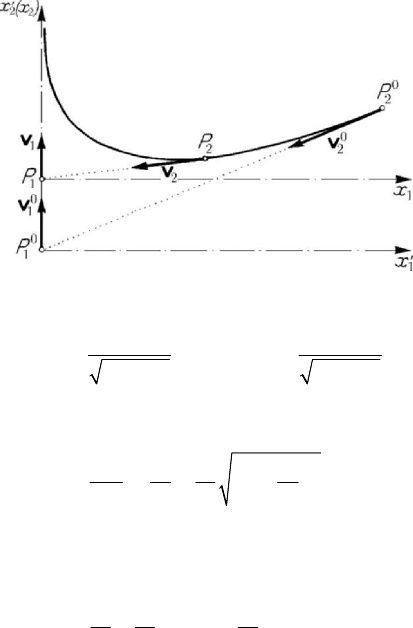
As well, we mention the meeting problem of a particle
1
P , which has a rectilinear
and uniform motion of velocity
1
v , and a particle
2
P , which has a curvilinear and
uniform motion of velocity
2
v ; the latter velocity will be collinear with the vector
21
PP
, tangent to the trajectory of the particle
2
P , which has to be determined
(Fig.10.5). We choose an inertial frame of reference
0
112
Pxx
′
′
, linked to the initial
position
0
1
P of the particle
1
P , and a non-inertial frame
112
Px x , linked to a location of
the particle
1
P in uniform translation with respect to the first frame; in fact, this second
frame is inertial too, its motion being specified by the equations (we assume that the
two particles start from the points
0
1
P and
0
2
P , respectively, at the initial moment
0t = )
11
xx
′
= ,
21 2
xvtx
′
=+
. Observing that
22 21
versvPP=
v , we get the
differential equations, which determine the trajectory of the particle
2
P in the movable
frame, in the form (
2
v has the components
1
x and
2
x )
Figure 10.5. The meeting problem of two particles.
21
1
22
12
vx
x
xx
=−
+
,
22
21
22
12
vx
xv
xx
=− −
+
;
dividing member by member the two equations (eliminating the time
t ), it results
2
221 2
112 1
d
1
d
xxv x
xxv x
⎛⎞
=+ +
⎜⎟
⎝⎠
.
Observing that
2 1 21 1 1 21
d/d / (/d)d(/)x x xx x x xx
=
+ and integrating, we can
write the equation of the trajectory with respect to the movable frame in the form
(
)
(
)
12 12
//
11 1
2
2
vv vv
xx x
x
aa
−
⎡
⎤
=−
⎢
⎥
⎣
⎦
. (10.2.7)

MECHANICAL SYSTEMS, CLASSICAL MODELS
620
Eliminating
22
12
xx+ between the two differential equations, we may write
11212
()(/)xvxxx=+ ; taking into account the previous observation, as well as
(10.2.7), it results
22
12 1
11 1 1
11
ddd d
xx
txxx
vx v x
⎛⎞⎛⎞
=−=−
⎜⎟⎜⎟
⎝⎠⎝⎠
(
)
(
)
(
)
12 12
//
11 1
d
22
vv vv
xx x
a
aa a
−
⎡⎤
=− +
⎢⎥
⎣⎦
,
wherefrom, assuming that
12
vv
≠
,
12 12
//
11
1
12 12
(/) (/)
2
vv vv
xa xa
x
tt
vv vv
−
⎡
⎤
=− −
⎢
⎥
+−
⎣
⎦
. (10.2.7')
Calculating
11
()xxt= and then
22
()xxt
=
, we obtain the motion of the particle
along the trajectory. The equation of the trajectory with respect to the fixed frame is of
the form
12 12
//
11
21
21
12 12
(/) (/)
2
vv vv
xa xa
vx
xvt
vv vv
−
′′
′
⎡
⎤
′
=+ +
⎢
⎥
+−
⎣
⎦
. (10.2.7'')
The constants
a and t are specified by (10.2.7), (10.2.7') with the initial conditions
00
11 1
xx x
′
==
,
00
222
xxx
′
==
, for
0t
=
. For
1
0x → we have
2
0x → , tt→ if
12
vv< and
2
x →−∞, t →∞ if
12
vv> . As a consequence, if
12
vv< , then the
particle
2
P meets the particle
1
P at the moment tt
=
, at the point of co-ordinates
1
0x
′
= ,
21
xvt
′
= with respect to the inertial frame. But if
12
vv> , then the two
particles do not meet. The distance between them is given by
2
22
21 1 2
PP x x
=
+ , so that
(
)
(
)
(
)
(
)
12 12 12 12
// 1/1/
11 1 1 1
21
22
vv vv vv vv
xx x x x
a
PP
aa a a
−+−
⎡⎤⎡ ⎤
=+= +
⎢⎥⎢ ⎥
⎣⎦⎣ ⎦
; (10.2.8)
the minimum of this distance is obtained for
21
/2
12
1
12
vv
vv
xa
vv
−
⎛⎞
=
⎜⎟
+
⎝⎠
, (10.2.8')
so that
21
/2
112
2
1min
22
12
12
vv
av v v
PP
vv
vv
−
⎛⎞
=
⎜⎟
+
⎝⎠
−
(10.2.8'')

Other considerations on particle dynamics
621
at the moment
()
21
/2
12 1 2
22 22
12
12 12
2
vv
av v v v
tt
vv
vv vv
−
⎛⎞
=+
⎜⎟
+
⎝⎠
−−
. (10.2.8''')
If
12
vvv==, then we get the equation of the trajectory with respect to the movable
frame
22
1
2
2
xa
x
a
−
=
, (10.2.9)
the motion being specified by
(
)
2
11
1
ln
22
xx
a
tt
va a
⎡
⎤
=− +
⎢
⎥
⎣
⎦
; (10.2.9')
as well,
22
1
21
2
xa
PP
a
+
=
. (10.2.9'')
The two particles do not meet; the minimal distance between them is obtained for
1
0x =
at the moment t →∞ and is equal to /2a .
The particle
1
P
can be a man (master) and the particle
2
P
his dog.
2.1.3 General theorems in the relative motion
Let be a free particle P of mass m , the position of which is specified by the vector
′
r with respect to an inertial (fixed) frame of reference
123
Ox x x
′
′′′
and by the vector r
with respect to a non-inertial (movable) frame
123
Ox x x ; starting from the relation
O
′′
=+
rr r, where
O
′
r is the position vector of the pole of the non-inertial frame with
respect to the inertial one, and using the relations in Chap. 5, Sec. 3.1, we find the
relation
r
O
′
′
=++×
vv v rω , where
ω
is the angular velocity vector (the rotation
vector) of the movable frame. We obtain thus the relation between the momenta with
respect to the two frames in the form
O
mm
′
′
=
++×HH v r
ω
, (10.2.10)
with
r
m=Hv. Using the relation (A.2.37) between the absolute and the relative
derivatives of a vector, we can write
d
() ( )
d
rr
O
mmm m
tt
′
∂
′
=+× + +×+×+×
∂
HH
va r v rωωωω
,
wherefrom, taking into account (6.1.45) and (10.2.1'), (10.2.2), it results

MECHANICAL SYSTEMS, CLASSICAL MODELS
622
r
t
C
t
∂
===++
∂
H
HFFFF. (10.2.11)
However, this result was to be expected, taking into account (10.2.2'); we may state
Theorem 10.2.3 (theorem of momentum). The derivative with respect to time of the
momentum of a free particle, in a non-inertial frame of reference, is equal to the
relative force which acts upon the particle in that frame.
Analogously, we obtain
() ( )
O
r
t
OOC
tt
∂
∂
==×=×=+×+
∂∂
K
KrHrFMrFF
, (10.2.12)
where, taking into account (10.2.1'), we notice that
2
() ()( )
t
O
mr
′
×= ⋅ − − +⋅ ×
⎡⎤
⎣⎦
rF rr a r rωωωω; (10.2.13)
thus, we state
Theorem 10.2.4 (theorem of moment of momentum). The derivative with respect to time
of the moment of momentum of a free particle, in a non-inertial frame of reference, with
respect to its pole, is equal to the moment of the relative force which acts upon the
particle in that frame (the sum of the moment of the resultant of the given forces which
act upon the particle and the moment of the complementary forces), with respect to the
same pole.
The Theorems 10.2.3 and 10.2.4 lead to the relation
()
() ( ) () () ( )
O
r
t
OOOOOC
t
∂τ
τ = =τ =τ +τ +τ
∂
H
HFFFF
, (10.2.14)
obtaining thus
Theorem 10.2.5 (theorem of torsor). The derivative with respect to time of the torsor of
the momentum of a free particle, in a non-inertial frame of reference, with respect to its
pole, is equal to the torsor of the relative force which acts upon the particle in that
frame (the sum of the torsor of the resultant of the given forces which act upon the
particle and the torsor of the complementary forces), with respect to the same pole.
It results, as well,
(
)
2
dd d d d d d d
2
r
t
rr
t
FF
m
TvWWW===+=⋅=⋅+⋅FrFrFr
(10.2.15)
because, taking into account (10.2.1'), we have
dd0
C
FC
W
=
⋅=Fr; we may thus
state
Theorem 10.2.6 (theorem of kinetic energy). The differential of the kinetic energy of a
free particle with respect to a non-inertial frame of reference is equal to the elementary
work of the relative force which acts upon it in this frame (the sum of the elementary
work of the resultant of the given forces which act upon the particle and the work of the
transportation force).
