Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

Other considerations on particle dynamics

643

224

1 cos sin 2 ...

gR R

ωω

λλ

′′

=− + +

′′

′

, (10.2.49)

obtaining thus the terrestrial acceleration

g (the practical acceleration), as a function of

the gravity acceleration

′

(the theoretical acceleration), at any latitude on the Earth

surface; replacing

R by Rh

, we get g as function of the altitude h from the sea

level too. The terms which contain

()

/Rgω

′

can be, in general, neglected. Thus, we

obtain, with a good approximation, the relation which links the terrestrial acceleration

to the gravity one

1cos

⎛⎞

′

=−

⎜⎟

′

⎝⎠

. (10.2.50)

At the poles (

/2λπ

′

=±

) we have gg

′

; in reality, this equality is approximate,

because the Earth is not a sphere, but a spheroid and the distribution of masses is only

approximately with spherical symmetry. At the equator (

0λ

′

), at the sea level, we

get

⎛⎞

′

=−

⎜⎟

′

⎝⎠

; (10.2.50')

we notice that this result is an exact one, corresponding also to the formula (10.2.48').

Besides, the maximal difference

′

−

is obtained at the equator. Numerically, we

have

23 2

/ 3.4636 10 1/288.717 1/289 (1/17)Rgω

−

′

≅⋅≅ ≅=

, where we have

considered the Earth as a sphere of radius

6.371 10 cmR =⋅ and we have assumed

that

978.1 cm/sgg

′

≅≅ . Hence, if the Earth would be rotating about its axis with

an angular velocity of

17 1.240 10 rad/sω

−

≅⋅ , the particles situated at the equator

would be weightless.

In reality, the formulae obtained above have a certain degree of approximation, due

to the model of sphere assumed for the Earth. If one takes into account that the Earth is

a spheroid (e.g., in the classical theory of Clairaut), then one obtains the possibility to

determine the gravity acceleration

′

corresponding to a parallel on the Earth surface;

the theoretical acceleration

g may be thus calculated. As a matter of fact, even using

the formulae (10.2.48)-(10.2.50) one cannot obtain

g without knowing g

′

; but one can

state that the difference

0gg

′

−> is sufficiently small.

Using a model closer to the physical reality, one can establish the formula

980.60509 2.5028 cos 2 0.0003ghλ=− −, (10.2.51)

which gives the terrestrial acceleration in

cm/s , as a function of the geographical

latitude

λ (the practical latitude) and of the height h in cm , over the sea level. We

MECHANICAL SYSTEMS, CLASSICAL MODELS

644

find thus, at the sea level (

978.1 cm/s

g = at the equator (result used

before) and

983.1 cm/s

g = at the poles. At the latitude 45λ =° (which

corresponds with a good approximation for Bucharest too) one obtains

980.6 cm/sg

= which represents the mean of the extreme values of the terrestrial

acceleration. We notice that

(

)

/ 0.0050989

ggg

−

= , so that the theoretical

acceleration has a variation of maximum

0.5% .

Projecting the relation (10.2.45) on the practical vertical

QP (Fig.10.12), we get

cos cos cos( )

mg mg mRαωλλα

′′′

=− +

;

if we put

mm= , neglect the angle α with respect to λ

′

, and take

cos 1α ≅

, then

we find again the formula (10.2.50) for

Observing that

cosgg α

′′

⋅=gg

, the formula (10.2.48) leads to

22 242

2cos cosgg gg Rαω λ

′

′′

+− =

;

taking into account (10.2.48'), we find

cos 1 cos

αλ

′

⎛⎞

′

=−

⎜⎟

′

⎝⎠

, (10.2.52)

relation which puts into evidence the degree of approximation of the formula (10.2.50)

(approximation

cos 1α ≅

). We may then also calculate (we take further into

consideration the relation (10.2.48'))

sin sin 2 sin 2

RgR

ggg

ωω

αλ λ

′

; (10.2.52')

as a matter of fact, this relation could be obtained as projection of the relation (10.2.45)

on a normal to the theoretical vertical

′

(Fig.10.12). The relations (10.2.52),

(10.2.52') are exact, in comparison with the relations (10.2.46') and correspond to the

relation (10.2.46) (for

1k = ). As well, the calculation of the angle

max

α for 45λ

′

=°

is justified too.

The formula (10.2.52) is an exact one in the frame of the spherical model used for

the Earth. Eliminating

Rω between (10.2.52) and (10.2.52'), we find the relation

sin

sin( )

λα

′

, (10.2.53)

which is exact too. As a matter of fact, this result may be obtained by projecting the

relation (10.2.45) on a normal to the centrifugal force

F (Fig.10.12).

Other considerations on particle dynamics

645

2.2.8 Deviation towards the east in the free falling of a heavy particle

Let us return to the equations of motion of a heavy particle at the Earth surface

(10.2.33'), where we take

F0, and let us put ()

Pgg

′

≅f , corresponding to

the results of the preceding subsection. The first approximation (10.2.35) with the

initial conditions (10.2.36) leads to

(0)

xvtx=+,

(0)

xvtx=+,

(0)

20 0

xgtvtx=− + +

. (10.2.54)

Assuming that the particle is falling from a height

h with the velocity

v from a point

of the local vertical (in what follows, by local vertical we mean only the theoretical

vertical, directed towards the centre of the Earth, considered to be spheric), we take

0xx==,

xh= ; in case of a free falling (

v0), the motion takes place as

the Earth would be fixed (in a first approximation the motion of rotation of the Earth is

neglected).

In a second approximation, the equations (10.2.35') with the initial conditions

(10.2.36') allow to write

()

(1)

3002

cos sin cos

xgt v v tλλλ=+−,

(1)

sinxvtλ=− ,

(1)

cosxvtλ= .

Remaining at this approximation (hence, neglecting

ω as well as higher powers of

ω ), we get the solution

()

300200

12311

( ) cos sin cos

xt gt v v t vt xωλ λ λω=+− ++

02 0 0

21 22

() sinxt v t vt xωλ=− + + , (10.2.54')

(

)

0200

31 33

() cos

xt v gt vt xωλ=−++

which contains also the influence of the motion of rotation of the Earth (in a first

approximation).

In case of a free falling of a heavy particle along the local vertical (

=v0) from the

height

h , we get

cos

xgtωλ=

xgth

−+; (10.2.55)

the results in Subsec. 2.2.1 are thus completed with a component in the positive

direction of the

Ox -axis. Hence, the heavy particle in free falling does not describe the

descendent vertical, but an arc of semicubic parabola

232

()cos

xhx

λ=−

, (10.2.55')

MECHANICAL SYSTEMS, CLASSICAL MODELS

646

and reaches the Earth after an interval of time

2/thg= with a deviation towards the

east (corresponding to

0x > , Fig.10.8) equal to

3/2

1max

cos

δλ==

. (10.2.55'')

Considering the mean value

980.6 cm/sg =

and taking into account (10.2.24), we

obtain

6 3/2

2.195 10 coshδλ

−

=⋅ , (10.2.55''')

where

h is taken in cm , the deviation being obtained in the same units. The

experimental verifications have put in evidence a good concordance with the theoretical

results. Thus, in 1831, Reich has made experiments in the mines of Freiburg (to avoid

the influence of the wind and of the other influences at the Earth surface), at a latitude

51λ =° and a falling height

1.585 10 cmh

⋅ ; the average value

exp

2.83 cmδ =

of 106 experiments has been in good correspondence with the theoretical result

2.76 cmδ = . We notice that for a height

10 cmh

one has 2.195 cosδλ

, and

the deviation is obtained in cm; e.g., at Bucharest (

45λ

° ) one has 1.55 cmδ = . At

the poles (

/2λπ=± ) we get 0δ

. The maximal deviation takes place at the equator

(

0λ = ,

978.1 cm/sg =

) and is given by

63/2

2.198 10 hδ

−

⋅ (δ and h in cm );

hence,

max

2.20 cmδ ≅ in free falling from

10 cm 100 mh

= .

If we launch a heavy particle along the ascendent local vertical (

=r0,

0vv==,

0v > ), we get

302

cos cos

xgt vtωλωλ=−,

xgtvt=− + ; (10.2.56)

the component

vgtv=− + of the velocity along the vertical vanishes at the moment

/tvg

′

= , for which we get

()

xt v

′

()

() cos 0

xt v

′

−<,

()

() cos 0vt v

′

−<.

The rotation of the Earth about its axis leads thus to a deviation towards the west of the

particle. Taking the position and the velocity at the moment

′

as initial conditions and

studying further the motion of the particle, we find that it takes place also in a plane

normal to the local meridian; the particle returns on the Earth at the moment

22/ttvg

′′ ′

at the point of co-ordinates

()xt

′

(

)

(4/3) /gω−

()

cosv λ

2()xt

′

= 0

() 0xt

′′

= , tangent at the vertical of this location (

() 0vt

′′

= ,

Other considerations on particle dynamics

647

()vt v

′′

=− ); it results further a deviation towards the west, equal to that obtained in

case of the ascendent motion (unlike the case of the free falling, the influence of the

velocity

() 0vt

′

< takes place).

In case of an approximation of higher order, when terms in

ω intervene too, it is

necessary to take into account the variation of

g with the height, as well as the force of

attraction of the Moon.

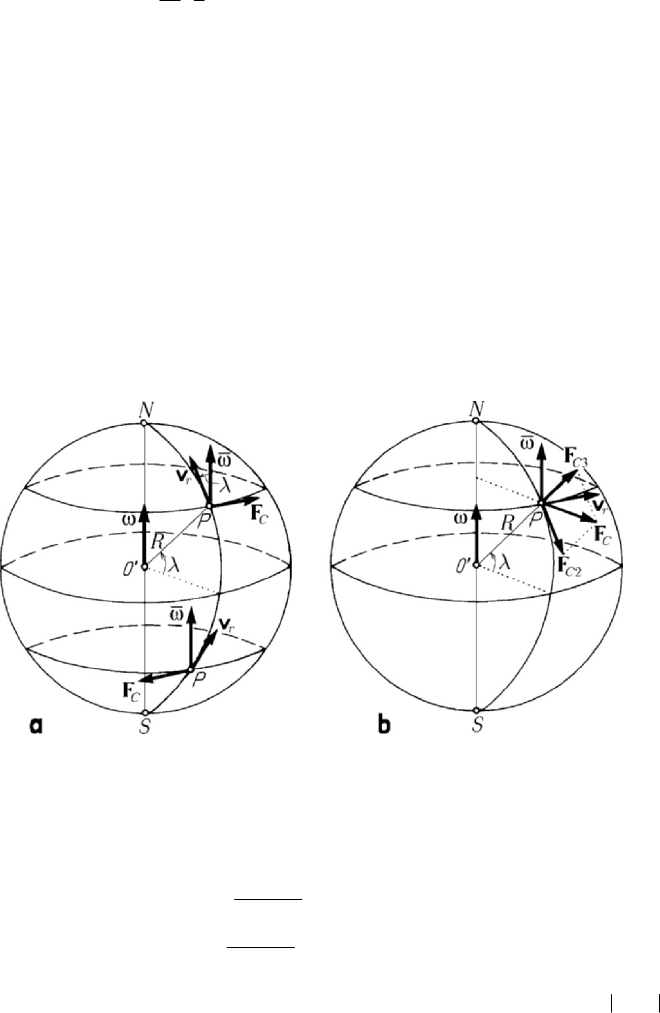
2.2.9 Coriolis’ force. Baer’s law

The deviation along a tangent to the local parallel, considered in the preceding

subsection, is due to the action of Coriolis’ force

−×Fv

. The equations of

motion of the heavy particle (10.2.33') read (with respect to the local frame of

reference, Fig.10.8)

12 3

2( sin cos)xx xωλ λ=−   ,

2sinxxωλ

−  ,

2cosxgxωλ

−+  ,

(10.2.57)

in the absence of the centrifugal force; integrating, with the initial conditions

(0) =rr

(0) =vv

, we can write

(

)

(

)

[

]

000

122 33 1

2sin cosxxx xx vωλ λ=− −− + ,

(

)

211 2

2sinxxxvωλ

−− + , (10.2.57')

(

)

3113

2cosxgt xx vωλ

−+ − + .

This system of linear differential equations can be easily integrated; as a matter of fact,

eliminating

x and

x between the first equation (10.2.57) and the last two equations

(10.2.57'), we get

(

)

220 0 0

11 1 2 3

442cos2sincosxx xgt v vωωωλωλ λ+=+ + − . (10.2.57'')

By integration, it results

()

(

)

00 0

132 1

1cos

( ) cos sin (1 cos 2 ) sin 2

xt v v t v t

λλ ω ω

ωω

⎡⎤

=− − − − −

⎢⎥

⎣⎦

cos

(10.2.58)

Replacing in the last two equations (10.2.57') and integrating, we obtain also the

solutions

()

(

)

00 0

232 1

sin cos

( ) cos sin sin 2 (1 cos 2 )

xt v v t v t

λλ

λλω ω

ωω

⎡⎤

=− − + − −

⎢⎥

⎣⎦

()

200 0

23 2

sin 2

cos cos sin

tvvtx

λλ λ−+ ++

(10.2.58')

MECHANICAL SYSTEMS, CLASSICAL MODELS

648

()

(

)

00 0

332 1

cos cos

() cos sin sin2 (1 cos2 )

xt v v t v t

λλ

λλω ω

ωω

⎡⎤

=−+−−

⎢⎥

⎣⎦

()

200 0

23 3

sin

sin cos sin

tvvtx

λλ λ−+ ++

(10.2.58'')

With the aid of the series expansions

sin 2 2 (2 ) /6 ...tt tωω ω

−+,

cos2 1 (2 ) /2 ...ttωω=− + and neglecting the terms in

ω or of higher degree, we

find again the solution (10.2.54'), obtained in the preceding subsection; as a matter of

fact, in the following considerations we will use this solution, which puts in evidence

(from a qualitative point of view), in a simpler way, various mechanical phenomena.

If we assume that the heavy particle is launched in a meridian plane (

0x = ), then

we take

=r0 and

0v = ; we obtain

()

3002

123

( ) cos sin cos

xt gt v v tωλω λ λ=+−

, (10.2.59)

so that the particle is deviated from the initial plane. As well, if the particle is launched

in a plane normal to the local meridian (

r0 and

), it results

() sinxt v tωλ=− , (10.2.59')

hence a tendency of deviation from this plane.

Let us consider the motion in a plane tangent to the Earth sphere (

0x = ) at the

considered location (we take

r0 and

); we can write (with respect to the

local frame of reference, Fig.10.8)

3020

121

() cos sin

xt gt v t vtωλωλ=++

02 0

21 2

() sinxt v t vtωλ=− + , (10.2.60)

(

)

() cos

xt v gtωλ=−

We notice that

2cosgvωλ

(taking into account (10.2.24), we have

2cosgvωλ> , even if the component

v of the initial velocity is equal to the second

cosmic velocity); it results

() 0xt

. Hence, the particle remains on the Earth surface

and we may assume that the motion (in the vicinity of the initial position with respect to

the Earth sphere) takes place in the tangent plane

. A constraint force N

(normal to the tangent plane, hence along the local vertical), which impedes the particle

to leave the plane

0x = is also acting in this case. The theorem of kinetic energy

(10.2.16') allows to write

Other considerations on particle dynamics

649

(

)

rrr

mv m

⋅+⋅=gv Nv ,

so that

const

= (result which can be accepted with a good approximation).

We can thus express the components of the velocity in the form

() cosvt v α= ,

() sinvt v α= , where ()tαα

is the angle made by the velocity

v with the

Ox -

axis. Replacing in one of the first two equations (10.2.57) (where we make

0x = ),

we find, after identification,

2sinαωλ

− ; hence,

() 2 sinttααωλ

− . (10.2.61)

Thus, we get

Theorem 10.2.12 (Baer’s law). In the boreal hemisphere, the angle α decreases,

corresponding to a deviation towards the right of the heavy particle, while in the

austral hemisphere the angle

α increases, corresponding to a deviation towards the

left of it.

Figure 10.13. Action of the Coriolis force upon a particle on the Earth surface: launching along

the tangent to the meridian (a); launching in the boreal hemisphere

along the tangent to the parallel towards the east (b).

Taking into account (10.2.61), one can show, by integration, that

() sin( 2 sin )

2sin

xt tαωλ

ωλ

=− − ,

() cos( 2 sin )

2sin

xt tαωλ

ωλ

=−,

so that the trajectory of the particle is circular; the radius of the circle is

/2 sinv ωλ

and is very great (we take into account (10.2.24)) and we can approximate it by its

tangent at the initial moment.

MECHANICAL SYSTEMS, CLASSICAL MODELS

650

We notice that, with respect to the gravity force, we have

2 / 2 / 1.487 10

rr r

mmgvg vω

−

×≤≅⋅vω , where

is expressed in m/s ; it

results that Coriolis’ force may be, in general, neglected in case of a particle subjected

to relative small velocities.

Let us consider, in particular, the case in which the particle

P is launched in the

boreal hemisphere, along the tangent to the meridian, e.g., towards the north

(Fig.10.13,a); in this case, Coriolis’ force will be directed towards the east, tangent to

the parallel which passes through

P , having the magnitude 2sin

Fmvωλ

. From

(10.2.59) we obtain a deviation towards the east given by

302

() cos sin 0

xt gt vt

ωλω λ

+>.

If the particle

would be moving along the meridian towards the south point, then the

Coriolis’ force would be directed towards the west. In both cases corresponds a

deviation towards the right, in conformity to Baer’s law. In the austral hemisphere, the

phenomenon is symmetric to that of the boreal hemisphere, with respect to the

equatorial plane; thus, if the relative velocity is directed towards the north point, then

Coriolis’ force will be directed towards the west. Coriolis’ force vanishes at the equator

and is maximal at the poles (

max

Fmvω

); starting from one of the poles, the

deviation will always take place towards the west. Thus, after a time

, the distance

will be travelled through, corresponding a linear deviation

vtω and an angular

deviation equal to

vt vt tωω= , hence equal to the angle by which the Earth is

rotating in that interval of time. Hence, a projectile launched from a pole has a

rectilinear trajectory; its apparent deviation is due to the fact that the Earth is rotating.

Thus, after 1 min 30 s one obtains an angular deviation of

0.0065628

rad, hence of

approximative

22 34

′′′

, which cannot be neglected.

The effect of Baer’s law is considerable in case of great continuous mechanical

systems. For instance, the right bank of the rivers which run from the south towards the

north or from the north towards the south, in the boreal hemisphere, is caving more then

the left bank; we mention thus the rivers at the north of Asia (which run from the south

to the north), which have the tendency of displacement towards the east. Due to the

Coriolis force too, at the railway lines which are directed approximately along a

meridian, being travelled through in a unique direction, the rail at the right is subjected

to a greater wear (the east rail if the direction of circulation is from the south to the

north or the west one in case of a circulation in the opposite direction). As well, the

trade winds are directed towards the equator; the colder air (hence, heavier) tends to

replace the warmer one (hence, lighter) in the boreal hemisphere from the north towards

the south, while in the austral hemisphere from the south towards the north. Indeed, the

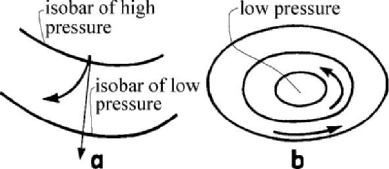
wind is a mass of air in motion; in the absence of the Coriolis force, the direction of the

motion corresponds to the gradient of the atmosphere pressure (from a high pressure to

a low one, normal to the isobar lines). The intervention of the Coriolis force leads to a

deviation towards the west (Fig.10.14,a) for the boreal hemisphere. In the state of

equilibrium, the configuration of the wind is stationary; Coriolis’ force is in equilibrium

with the forces due to the pressure, so that the wind becomes parallel to the isobar lines.

Other considerations on particle dynamics

651

A zone of low pressure surrounded by isobar lines forms a cyclone. Due to Coriolis’

force, the wind is circulating around the cyclone, counterclockwise in the boreal

hemisphere (Fig.10.14,b) and clockwise in the austral one.

Figure 10.14. Formation of trade winds (a) and of cyclones (b) in the boreal hemisphere.

Let us study now the case in which the particle

P is launched, in the boreal

hemisphere, along the tangent to the parallel, e.g., towards the east (Fig.10.13,b); in this

case, the Coriolis’s force is contained in the meridian plane and is normal to the poles’

line, being directed towards the exterior of the Earth (the same direction as the

centrifugal force) and having the magnitude

Fmvω

. We decompose the force

F in two components: the force

F along the ascendent local vertical, which has the

tendency to make smaller the weight of the particle, and the force

F , tangent to the

meridian and directed towards the south, which has the tendency to deviate the particle

in that direction (in conformity to the formula (10.2.59')); if the particle

P is launched

in the austral hemisphere, towards the east too, then to the component

F of Coriolis’

force corresponds a deviation towards the north (hence, in both cases, towards the

equator). In the case in which the particle is launched towards the west, in any of the

two hemispheres, Coriolis’ force and its components have an opposite direction; thus,

the component

F has the tendency to augment the weight of the particle, while the

component

F leads to a deviation towards the poles (towards the north in the boreal

hemisphere and towards the south in the austral one).

The effects of the Coriolis’ force can be put into evidence at the atomic level too.

Thus, the polyatomic molecules have an aggregate motion of rotation, while the atoms

oscillate around their positions of equilibrium; hence, the atoms are in relative motion

with respect to a frame rigidly linked to the molecule. The Coriolis’ forces are non-

zero, leading to a displacement of the atoms in a direction normal to that of the original

oscillations.

2.2.10 Foucault’s pendulum

Let us consider the motion of a heavy particle on a fixed sphere at the Earth surface

in the boreal hemisphere; the spherical pendulum thus obtained is called the Foucault

pendulum, after Léon Foucault, who made a famous experiment with such a pendulum

in 1815, at the Pantheon, in Paris. We assume that the particle

P (in fact a spheric

ball), of mass

m , is hanged up at the end of a flexible and inextensible thread, of length

l , fixed at the pole O of the local (non-inertial) frame of reference. The equation of

motion is written in the form

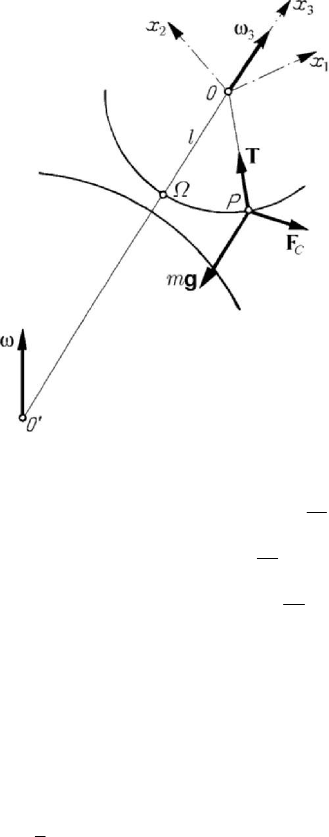
MECHANICAL SYSTEMS, CLASSICAL MODELS

652

mmm

−×+a

, (10.2.62)

where

T is the tension in the thread (the constraint force arises because the particle is

constrained to stay on the sphere of centre

O and radius l ) and where the influence of

the centrifugal force has been neglected with the respect to Coriolis’s force (

ω has

been neglected with respect to

ω ). In components, we obtain (Fig.10.15)

Figure 10.15. The Foucault pendulum.

()

123

2sincos

mx m x x T

ωλ λ=−−  

2sin

mx m x T

ωλ=− −  , (10.2.62')

2cos

mx mg m x T

ωλ=− + −  ;

the relation of holonomic and scleronomic constraint

2222

123

0xxxl

+−= (10.2.62'')

is added to these equations. The elementary work of the constraint force is, in this case,

equal to zero, so that the theorem of kinetic energy (10.2.15') leads to

(

)

ddd

mv m mg x=⋅=−gr , (10.2.63)

wherefrom we get the first integral of energy