Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics
Подождите немного. Документ загружается.


Other considerations on particle dynamics
673
We notice that one may write the relation (10.3.29) also in the form
d
dd ( )
m
TW T
m
=+ ⋅−
Hu ; (10.3.29')
introducing the relative velocity
=
−wuv and the reactive force m
=
Rw, it results
2
ddd
2
R
v
mWW
⎛⎞
=+
⎜⎟
⎝⎠
, (10.3.29'')
too, where
dd
R
W =⋅Rr
is the elementary work of the reactive force. Thus, we state
Theorem 10.3.12' (theorem of kinetic energy; second form). The product of the mass of
a particle of variable mass by the differential of its kinetic energy, assuming that it has
a mass equal to unity, is equal to the sum of the elementary work of the resultant of the
given forces which act upon the particle and the elementary work of the reactive force.
Dividing by
dt , we may also write
2
d
d2
R
v
mPP
t
⎛⎞
=+
⎜⎟
⎝⎠
, (10.3.29''')
so that we can state
Theorem 10.3.12'' (theorem of kinetic energy; third form). The product of the mass of
a free particle of variable mass by the derivative of its kinetic energy with respect to
time, assuming a mass equal to unity, is equal to the sum of the power of the resultant
of the given forces which act upon the particle and the power of the reactive force.
In the case in which the absolute velocity of the masses emitted or captured is equal
to zero (
=
u0), we obtain
2
1
ddd
2
TvmW+=
(10.3.30)
or
1
d( ) dmT W
m
=
; (10.3.30')
if the relative velocity of these masses vanishes (
=
w0, hence
=
uv
), then it results
2
1
ddd
2
TvmW−=
, (10.3.31)
as well as
2
dd
2
v
mW
⎛⎞
=
⎜⎟
⎝⎠
(10.3.31')
or

MECHANICAL SYSTEMS, CLASSICAL MODELS
674
2
d
d2
v
mP
t
⎛⎞
=
⎜⎟
⎝⎠
. (10.3.31'')
One can thus state corresponding theorems for the two problems of Levi-Civita.
If the absolute velocity u of the emitted or captured masses is normal to the velocity
v of the particle (
0⋅=uv ), then we get the same results as in the case =u0.
3.2 Motion of a particle of variable mass in a gravitational field
We present, in what follows, the motion of a particle of variable mass in a
gravitational field; we mention, especially, the motion along a vertical, in vacuum or in
a resistent medium, in case of a linear or exponential variation of mass. As well, we
consider the motion of a particle in a fixed plane (the external ballistics problem).
3.2.1 Tsiolkovskiĭ’s second problem
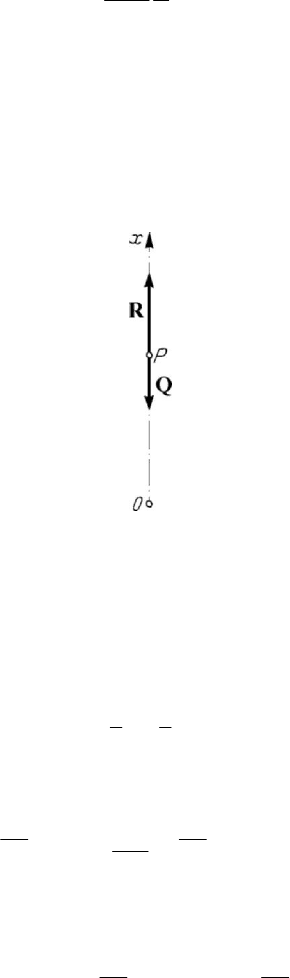
Let be a free particle
P
of variable mass, which is moving along the local vertical;
in Tsiolkovskiĭ’s second problem one assumes that the particle, of weight
mg , is
launched up with an initial velocity
0
v , at the moment
0t
=
, the relative velocity
const=
J
JJJJG
w of the emitted masses being descendent (in this case, the reactive force is
directed towards up, because
0m
<
, Fig.10.21). Taking the
Ox
-axis along the
ascendent vertical, we may write Meshcherskiĭ’s equation (10.3.1'') in the form
(neglecting the air friction)
Figure 10.21. Tsiolkovskiĭ’s second problem.
mv mg mw
=
−−
or in the form
d
ln ( )
d
vgw ft
t
=− −
;
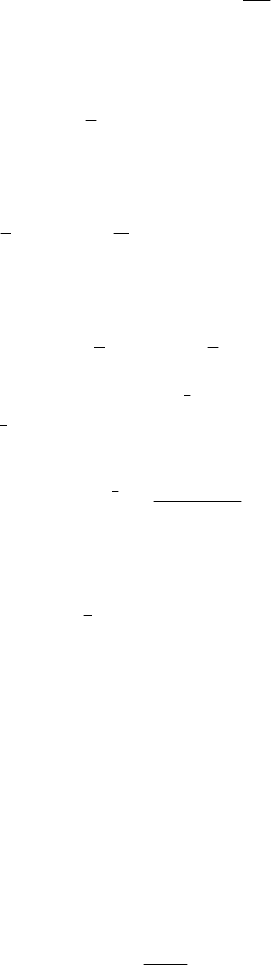
Other considerations on particle dynamics
675
taking into account the conditions at the initial moment
0t
=
(
0
mm
=
,
0
=vv), it
results the velocity
0
0
() ln
m
vt v gt w
m
=−+
, (10.3.32)
the position of the particle
P being given by ( (0) 0x
=
)
2
0
0
1
() ln ( )d
2
t
xt gt vt w f ττ=− + −
∫
. (10.3.32')
In case of a linear variation of mass, given by (10.3.12), we obtain
[]
2
0
1
() (1 )ln(1 )
2
w
xt gt vt t t t
ααα
α
=− + + − − + , (10.3.33)
while in case of an exponential variation of mass of the form (10.3.12'), we have
22
0
11
()
22
xt gt vt wtα=− + + . (10.3.33')
The particle reaches a height for which
() 0vt
=
; in case of the motion given by the
law (10.3.33'), we get
0
/( )tv g wα=−, so that
2
0
()
2( )
v
hxt
gw
α
==
−
. (10.3.34)
If
/gwα = , then one observes that
0
vv
=
, the motion being uniform (relative
equilibrium), while if
/gwα > , then the reactive force is greater than the weight.
From the expression of the time
t it results /gwα
<
, so that the particle is moving in
a field of acceleration
0gwα
−
> ; one observes thus that the formula (10.3.34)
corresponds to Torricelli’s formula (7.1.17).
3.2.2 Motion of a particle of variable mass along a vertical, in a field of Newtonian
attraction
As above, we consider the motion in vacuum of a particle
P of variable mass along
the local vertical, with an initial velocity
0
v , directed towards up, assuming an
exponential variation of mass, of the form (10.3.12'); we suppose that the particle is
acted upon by a Newtonian force of attraction, in inverse proportion to the square of the
distance between the particle and the centre
O of the Earth. Meshcherskiĭ’s equation of
motion (10.3.1'') reads
2
0
2
gR
mv m mw
x
=− −
,
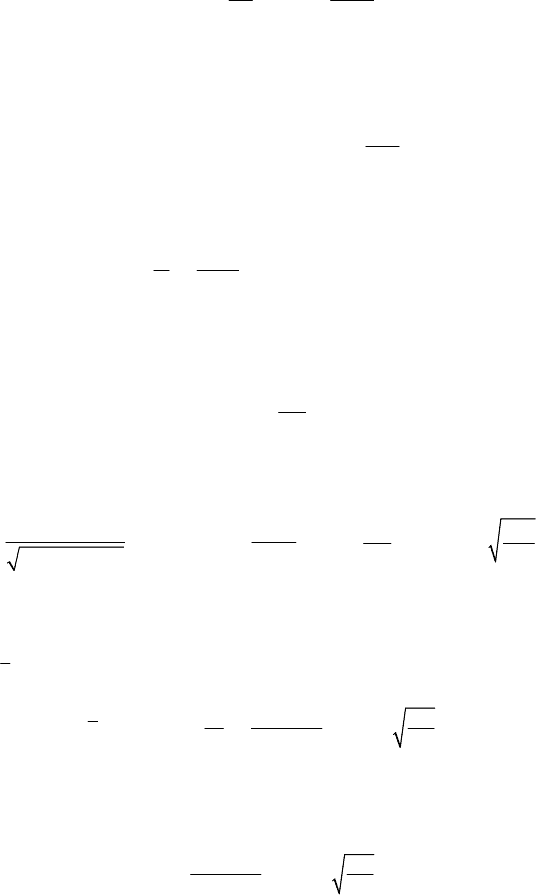
MECHANICAL SYSTEMS, CLASSICAL MODELS
676
where
0
g is the gravity acceleration at the Earth surface (at the sea level), for xR= ,
the
Ox -axis being along the ascendent vertical. Taking into account the variation of
mass, we obtain (
d/dvxt= )
2
0
2
d
d
gR
v
vw
x
x
α=−
and, integrating with respect to
x , with the condition
0
vv
=
for xR
=
, the velocity
is given by
(
)
0
22
0
2( )
gR
vv xRw
x
α=+ − − . (10.3.35)
By a change of variable
(1 )xR z
=
+ , we can write
()
23
1
1
1
R
zz z
xz
==−++
+
O
,
where we neglect
3
z and higher powers for heights x relative small. The relation
(10.3.35) becomes
()
22 3
00
0
21
w
vv gRz z z
g
α
⎛⎞
=+ −++
⎜⎟
⎝⎠
O ,
wherefrom (we notice that
d/dvRzt
=
)
2
d
d
z
t
zz
λ
αβ
=
++
,
2
0
0
2
v
gR
α =
,
0
1
w
g
α
β
=
−
,
0
2g
R
λ =
. (10.3.36)
If we take
xR= , hence 0z
=
for 0t
=
, and if we assume that
0
0v = , hence
0α = , then we get, by integration,
2
(1 cosh )/ 2 sinh ( / 2)ztβλβλ=− = ; the
height
xxRRz=− = with respect to the Earth surface is given by
00
22
0
sinh sinh
22
wg g
t
xR R t
gR
α
λ
β
−
==
. (10.3.36')
Denoting by
1
t the time in which the active line segment is travelled through, its
length results in the form
00
2
1
0
sinh
2
wg g
hRt
gR
α
−
= , (10.3.37)
the velocity at its end being given by
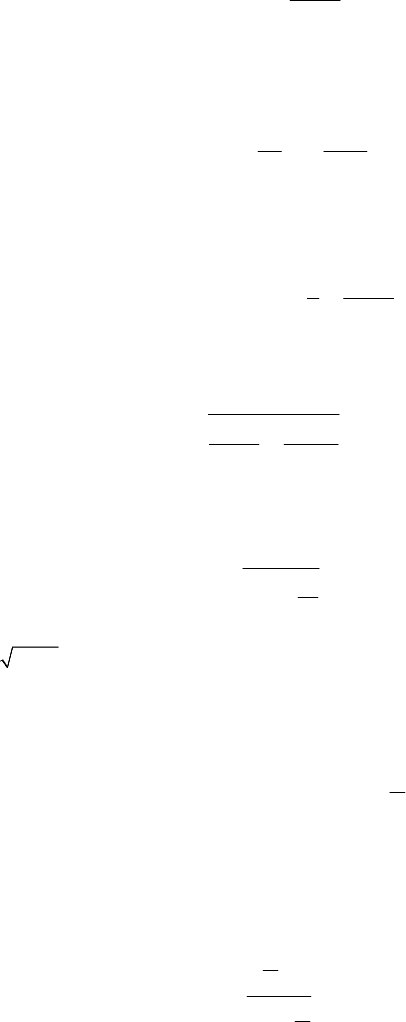
Other considerations on particle dynamics
677
(
)
0
2
1
2
gR
vhw
Rh
α=−
+
. (10.3.37')
The motion of the particle
P along the passive segment of a line is governed by the
equation (with
11
()mmt= )
2
0
11 1
2
d
d
gR
v
mv mv m
x
x
==−
,
which leads to (with the condition
1
vv
=
for xRh
=
+ , at the end of the active
segment of a line)
(
)
22 2
0
1
11
2vv gR
xRh
=+ −
+
;
for
0v = we obtain the total height HxR
=
− , given by
2
1
2
0
1
1
2
HR
v
Rh
gR
=
−
−
+
. (10.3.37'')
In case of an instantaneous combustion (
0h
=
), we have
2
1
2
1
0
2
v
H
v
g
R
=
−
; (10.3.37''')
if
0
1
2vgR , then we find again Torricelli’s formula, corresponding to the case of
the particle of constant mass.
The study may be performed for an arbitrary
x too.
Let us consider now for the mass of the particle
P a linear variation of the form
00
1
(1 ) 1
t
mm t m
t
αβ
⎛⎞
=−= −
⎜⎟
⎝⎠
,
where
00
1
()/mmmβ
=
− ,
1
m being the mass at the end of the active segment (at the
end of the combustion,
1
tt= ) while
0
1
mm
−
is the consumed mass. The equation of
motion reads
1
1
1
w
t
vg
t
t
β
β
=
−
−
,
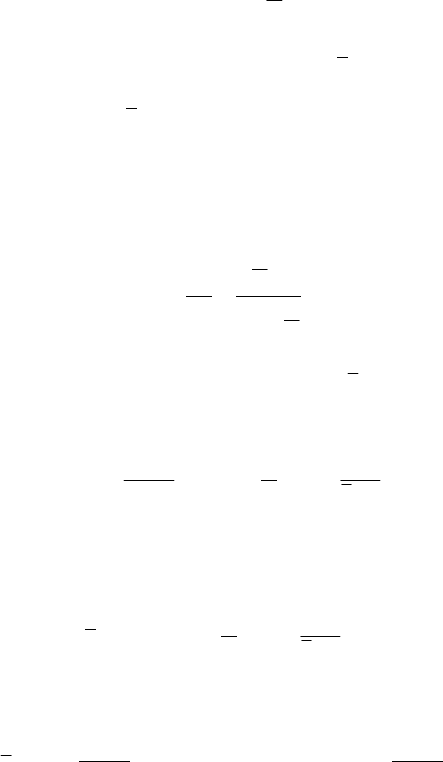
MECHANICAL SYSTEMS, CLASSICAL MODELS
678
where
22
0
/ggRx= is the gravity acceleration,
0
gg
=
taking place for xR= (at
the Earth surface – sea level). Assuming, at the beginning, that
0
constgg
=
= , we
obtain
0
1
ln 1
t
vw gt
t
β
⎛⎞
=− − −
⎜⎟
⎝⎠
;
at the end of the active segment, we may write (
11
()vt v
=
)
0
11
ln(1 )vw gtβ
=
−−−, (10.3.38)
this formula being used in external ballistics.
If we take into account the variation of
g
with the altitude, then we have to integrate
the equation
2
1
0
2
1
0
1
w
t
R
xg
t
x
t
β
β
+
−=
−
,
observing that we can consider
00
() ( )mmft mfx==
, it results (we have
d/dxvvx= )
2
2
0
1
1
d
22
()
Rh
R
Rx
vg R w
Rh t
f
x
β
+
⎛⎞
=−+
⎜⎟
+
⎝⎠
∫
, (10.3.39)
where
1
vv
=
and xRh=+ for
1
tt
=
. Integrating, analogously, the equation of
motion for which one takes, with approximation,
0
gg
=
, we read
2
0
1
1
d
22
()
Rh
R
x
vghw
t
f
x
β
+
=− +
∫
; (10.3.39')
subtracting one formula from the other, it results, finally,
[]
22
2
22
000
11 1
2ln(1)2
hh
vv g w gt g
Rh Rh
β=+ = −+ +
+
+
, (10.3.38')
where we took into account (10.3.38). We get thus the velocity at the end of the active
segment, as a function of the altitude at the respective moment. We notice that in the
formula (10.3.39') it has been taken the same function
()xxt
=
to express the mass
variation
0
()mmft= as in the formula (10.3.39), which can be assumed only as a
first approximation.
The acceleration at the end of the combustion (for
1
tt
=
we have
1
gg= ) reads
Other considerations on particle dynamics
679
1
1
1
w
g
t
β
γ
β
=
−
−
. (10.3.40)
3.2.3 Rectilinear motion of a particle of variable mass in a resistent medium
Let us, further, consider the motion of a particle
P
of variable mass along the local
vertical, with an initial velocity
0
v , directed towards up in a resistent medium; we
assume that the mass is varying in time after the linear law (10.3.12). Meshcherskiĭ’s
equation of motion (10.3.1'') is written in the form (the resistance
Q and the relative
velocity
w
are directed opposite to the motion, Fig.10.22)
Figure 10.22. Rectilinear motion of a particle of variable mass in a resistent medium.
()mv Q v mw
=
−−
. (10.3.41)
If the magnitude of the resistance is proportional to the velocity (
0
Qmkv=
,
constk =
) and if we take, in general,
0
()mmft
=
, we obtain
0
kf
vvw
f
f
+
+=
,
wherefrom
dd
() ()
()
() e e d
()
tt
kk
ft ft
ft
vt C w t
ft
−
⎡
⎤
∫∫
=−
⎢
⎥
⎣
⎦
∫
, constC
=
. (10.3.42)
Observing that
() 1
f
ttα=− and by the initial condition
0
(0)vv
=
, we get
(
)
/
0
() (1 )
k
ww
vt v t
kk
α
αα
α
=− − +; (10.3.42')
integrating once more and taking
(0) 0x
=
, we obtain
MECHANICAL SYSTEMS, CLASSICAL MODELS
680
(
)
()/
0
1
() 1 (1 )
k
ww
xt t v t
kk k
αα
αα
α
α
+
⎡
⎤=+ − −−
⎣
⎦
+
. (10.3.42'')
If the magnitude of the resistance is proportional to the square of the velocity
(
2
0
Qmkv=
), then one integrates the equation
2
(1 )tv w kvαα−=−
,
by separating the variables; we put the initial condition
(0) 0v
=
and get
2/
2/
1(1 )
1(1 )
kw
kw
t
w
v
k
t
α
α
α
α
α
−−
=
+−
. (10.3.42''')
For
/kw α sufficiently great, we can take, with a good approximation, /vwkα≅ .
In aerodynamics one obtains
0
/2mk b Aρ
=
, where b is the aerodynamical
coefficient,
ρ is the air density, while A is a characteristic area of the body, modelled
as a particle; one obtains thus an approximative expression of the velocity in the form
0
0
2 Gw
v
bgA
α
ρ
=
, (10.3.43)
where
0
G and
0
g are the weight of the particle and the gravity acceleration at the
initial moment
0t = , respectively.
Let us consider now the projection on a horizontal line of the motion of a particle of
variable mass in a resistent medium (we take the
Ox -axis in the horizontal plane). We
assume that
2
Q
Qkv= and
2
P
Pkv= , where P is the lift (the ascensional force); if
Q
k and
P
k
are proportional to the air density, then the ratio /
PQ
kk=
is
independent on this density. It must be, permanently, an equilibrium between the
weight of the particle and the lift (
mg P
=
), so that the equation of motion (10.3.41)
reads
1
gw
v
t
α
α
=− +
−
,
where we considered a linear variation of the mass too. In the case in which
constx = ,
we get, by integration (with the initial condition
0
(0)vv
=
),
0
() ln(1 )
g
vt v t w tα=− − −
; (10.3.44)
integrating once more (with
(0) 0x
=
), it results
2
0
() ( ) (1 )ln(1 )
2
gw
xt v wt t t tαα
α
=+− + − −
, (10.3.44')

Other considerations on particle dynamics
681
hence the equation of motion of the particle on the active segment of a line. These
results allow to solve also some interesting problems of optimum.
3.2.4 The balloon problem
A problem in the frame of those studied above is that of a balloon of weight
m
g
,
which rises along the vertical by a continuous throwing of the ballast over the border.
We assume that the balloon is acted upon by an ascensional force
A , corresponding to
Archimedes’ theorem (hence, a force equal to the weight of a volume of air
corresponding to that of the balloon), and by the resistance of the air, the magnitude of
which is in direct proportion to the square of the velocity (
2
()Qv kv= ,
constk =
).
The equation of motion along the ascendent vertical reads
2
mx mg A kx mw=− + − + , (10.3.45)
hence it is a differential equation of the first order of Riccati’s type in
()xt , which may
be integrated by two quadratures if a particular integral is known.
If, e.g., the condition that the motion of the balloon be uniform is put
(
0
xv= ,
0
constv = ), then we get an equation with separate variables, which leads to
(with
constw = and the initial condition
0
(0)mm
=
)
()
2
0
//
0
() 1 e e
gt w gt w
Qkv
mt m
g
−−
−
=−+
. (10.3.45')
If the ballast
()Mt is thrown in a sufficiently long time, so that the factor
/
e
gt w−
be
practically zero for
() 0Mt → together with t →∞, then we have
(
)
2
00 0
/mM Qkvg−=− ,
0
(0)MM
=
, and the relation (10.3.45') leads to
/
0
() e
gt w
Mt M
−
= ; (10.3.45'')
hence, if the mass of the ballast varies after an exponential law, then the ascensional
motion of the balloon is uniform.
3.2.5 External ballistic problem
Let us consider a more general case of motion of a heavy particle
P
of variable
mass in the air, at the Earth surface. We assume that the trajectory is a plane curve (see
Subsec. 3.1.6 too), the particle being acted upon by the weight
m
g
, by the reactive
force
Rm==Rwτ ,
0m
<
(
τ
is the unit vector of the tangent to the trajectory in
the direction of the motion) and by the resistance
Q=−Q τ
, with
2
00
(/2) ( / )Qb Avρρρ= (Fig.10.23), where b is the aerodynamical coefficient, ρ
and
0
ρ represent the density of the air at a given height and at the Earth surface,
respectively, while
A is a characteristic area of the body modelled as a particle. We
notice that we can take, in general,
3
()( )bvxψϕ
=
, so that

MECHANICAL SYSTEMS, CLASSICAL MODELS
682
3
( )()QKhxfv= ,
0
1
2
KAρ=
,
33
0
() ()hx x
ρ
ϕ
ρ
= ,
2
() ()
f
vvvψ= . (10.3.46)
Denoting by
θ
the angle made by the tangent to the trajectory with the
1
Ox
-axis, we
have
1
cos /xvθ
=
,
3
sin /xvθ
=
so that we may write the equations of motion along
the considered axes in the form
1
13
( )()
x
Km
xhxfvw
mmv
⎡⎤
=− +
⎢⎥
⎣⎦
,
3
33
( )()
x
Km
xg hxfv w
mmv
⎡
⎤
=− − +
⎢
⎥
⎣
⎦
.
(10.3.47)
In Frenet’s frame of reference, of unit vectors
,
τ
ν , it results
Figure 10.23. The external ballistic problem.
3
sin ( )() 0
Km
vg hxfv w
mm
θ++ +=
,
2
cos cos 0
v
gvg
R
θθ θ
−
+=+=
, (10.3.47')
where we took into account the definition relation of the curvature radius
1/ d /d /Rsvθθ=− =−
. These equations are used in the external ballistics of the
projectiles of variable mass.
3.3 Mathematical pendulum. Motion of a particle of variable mass in
a field of central forces
The classical problems of the dynamics of a particle can be taken again in the case of
a particle of variable mass. In the following, we consider the mathematical pendulum of
variable mass and the motion of a particle of variable mass in a field of central forces.
3.3.1 Mathematical pendulum of variable mass
Let be a particle
P of variable mass and weight m
g
, constrained to move on a
circle of radius
l and centre O , situated in a vertical plane (Fig.7.9). We assume that
the motion takes place in vacuum, the absolute value of the emitted masses vanishing
