Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics
Подождите немного. Документ загружается.


Other considerations on particle dynamics
683
(
=u0). Observing that vlθ
=
, where ()tθθ
=
is the generalized co-ordinate which
specifies the location of the particle, the theorem of kinetic energy, written in the form
(10.3.30), leads to
()
22 22
11
ddsind
22
ml l m mglθθ θθ+=−
;
if we exclude the case of equilibrium (
0θ
≠
), then it results
2
sin 0
m
m
θθωθ++ =
,
2
g
l
ω
=
, (10.3.48)
obtaining an equation which generalizes the classical equation (7.1.38') of the
mathematical pendulum.
Writing the equation of motion
m
=
++
vFRR, m
=
− Rv, (10.3.49)
in projection on the principal normal, we obtain the magnitude of the constraint force
R
in the form (with the direction towards the pole O )
2
22
cos cos cos
vv
R m mg mg mg
lgl
θ
θθ θ
ω
⎡
⎤
⎛⎞
⎛⎞
=+ = + = +
⎢
⎥
⎜⎟
⎜⎟
⎝⎠
⎝⎠
⎢
⎥
⎣
⎦
. (10.3.49')
If the variation of mass is after an exponential law of the form
0
e
t
mm
α
= ,
constα = , then the equation (10.3.48) becomes
2
sin 0θαθω θ
+
+=
; (10.3.48')
it has thus the same form as the equation of the pendulum of constant mass in a resistent
medium, for which the resistance is proportional to the velocity (see Chap. 7, Subsec.
1.3.3).
In case of small oscillations around a stable position of equilibrium (
0θ = ) we can
take
sin θθ
≅
, and the equation (10.3.48) becomes linear
2
0
m
m
θθωθ
+
+=
. (10.3.48'')
Meshcherskiĭ considered the case of a mass with linear variation. Thus, if the mass
has a variation of the form
0
(1 )mm tα
=
− ,
0α >
, the equation (10.3.48) reads
2
0
1 t
α
θθωθ
α
−
+=
−
. (10.3.50)
By a change of variable
(1 ) /tταωα=− , one obtains Bessel’s equation

MECHANICAL SYSTEMS, CLASSICAL MODELS
684
2
2
d1d
0
d
d
θθ
θ
ττ
τ
+
+=
, (10.3.50')
the solution of which is written by means of Bessel’s function of the first species and of
order zero in the form
2
0
22
0
() () (1)
2(!)
n
n
n
n
CJ
n
τ
θτ τ
∞
=
==−
∑
; (10.3.50'')
we get
()
0
0
0
(1 )
()
Jt
t
J
ω
α
α
θθ
ω
α
⎡
⎤
−
⎣
⎦
=
, (10.3.50''')
with the initial condition
0
(/)θω α θ
=
for 0t
=
.
Figure 10.24. Mathematical pendulum of variable mass.
If the mass has a variation after the law
0
(1 )mm tα
=
+ ,
0α >
, then one obtains
the equation
2
0
1 t
α
θθωθ
α
+
+=
+
; (10.3.51)
in fact, Meshcherskiĭ has considered the equation (
0β > )
2
0
1 t
β
θθωθ
α
+
+=
+
, (10.3.51')
which has a somewhat more general character. By a change of variable
(1 ) /tταωα=+ and of function
()/2
(1 )t
βα α
ϑθ α
−
=+ , we obtain Bessel’s
equation

Other considerations on particle dynamics
685
22
22
d1d
10
d
d
n
ϑϑ
ττ
ττ
⎛⎞
++−=
⎜⎟
⎝⎠
,
2
n
βα
α
−
= , (10.3.51'')
which can be integrated with the aid of Bessel’s functions
n
J
±
, as n is an integer or a
fraction; in particular, if
βα
=
, then we find again the preceding result (changing the
sign, from
α
−
to α ).
In the general case in which
≠
u0, the theorem of kinetic energy, written in the
form (10.3.29) leads to
2
sin sin( )
mm
u
mml
θθωθ θϕ++ = −
. (10.3.52)
where
ϕ is the angle made by the absolute velocity u with the
Ox
-axis (Fig.10.24).
Analogously, one can study the motion of the mathematical pendulum in a resistent
medium.
3.3.2 Motion of a particle of variable mass in a field of central forces
We consider the motion of a particle of variable mass
()mmt
=
, 0m < , acted
upon by a central force, for which the relative velocity of the emitted masses vanishes
(
=w0). It is assumed that the central force is of attraction, its magnitude being in
inverse proportion to the square of the distance to the fixed point and in direct
proportion to the square of the mass; the equation of motion corresponding to the
Theorem 10.3.3 is written in the form
3
m
r
=−
rr; (10.3.53)
this situation may occur, for instance, in the study of the motion of a particle of variable
mass with respect to another particle having the same mass, both particles being acted
upon by forces of Newtonian attraction with a gravity constant equal to unity (
1
f
= ).
In conformity to the results in Subsec. 3.1.6, the trajectory is a plane curve.
Projecting on the co-ordinate axes
k
Ox , 1, 2k
=
, the equations of motion read
3
0
kk
m
xx
r
+=
, 1, 2k
=
,
222
12
rxx
=
+ ; (10.3.53')
by a change of function and of variable
p
kk
xmξ= , 1, 2k
=
, dd
q
mtτ
=
, (10.3.54)
where
,pq
∈
` must be determined, these equations become
2
2122
2
dd
(2 ) ( 1)
d
d
kk
pq pq p
k
mpqmmppmm
ξξ
ξ
τ
τ
++−−
++ +−
121
3
0
k
pp
k
pm m m
ξ
ξ
ρ
−−+
++ =
,
1, 2k
=
,
222
12
ρξξ
=
+
.
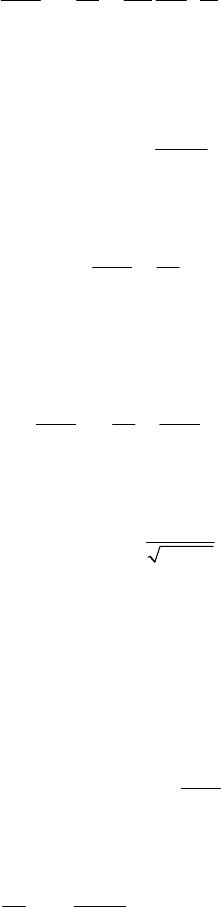
MECHANICAL SYSTEMS, CLASSICAL MODELS
686
For the sake of simplicity, we put
20pq
+
=
,
221pq p
+
=− +
, obtaining
1p =−
,
2q = ; the above equations take the form
(
)
2
2
2332
d
11d1
0
dd
k
k
m
mt
ξ
ξ
τρ
⎡⎤
++ =
⎢⎥
⎣⎦
, 1, 2k
=
. (10.3.54')
We suppose, after A.S. Lapin, that
22
d(1/ )/d 0mt
=
, hence that the law of mass
variation is of the form
0
1
m
m
t
α
=
−
, 0α > ; (10.3.55)
the equations of motion read
2
23
d
0
d
kk
ξξ
τρ
+
= , 1, 2k
=
, (10.3.55')
in this case. If, after MacMillan, we put
22234
0
d(1/ )/d /4mt m mα=− , constα = ,
the equations of motion become
2
2
23 4
0
d
1
0
d4
k
k
m
ξ
α
ξ
τρ
⎛⎞
+− =
⎜⎟
⎝⎠
, 1, 2k
=
, (10.3.56)
corresponding a law of mass variation of the form
0
1
m
m
t
α
=
−
, 0α > . (10.3.56')
Let us consider now the case of two particles P and P
′
of masses ()mmt= and
constm
′
= , respectively, acted upon by Newtonian forces of attraction, with a gravity
constant equal to unity (
1
f
=
). Assuming that the absolute velocity of the emitted
masses vanishes (
=u0) and using the law of mass variation (10.3.55), we can write
the vector equation of motion of the particle
P with respect to the particle P
′
(chosen
as origin) in the form
3
mm
mm
r
′
=− −
vrv; (10.3.57)
the corresponding scalar equations read
3
0
1
kk k
m
xx x
t
r
α
α
′
++ =
−
, 1, 2k
=
,
222
12
rxx
=
+ . (10.3.57')
By a change of function and variable
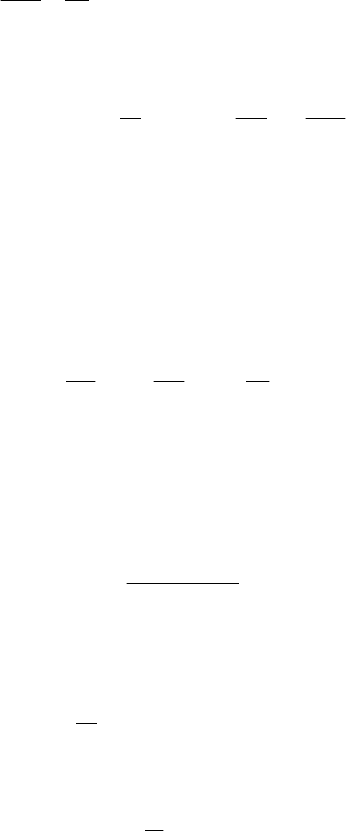
Other considerations on particle dynamics
687
2
(1 )
kk
xtαξ=− , 1, 2k
=
,
3
d(1 )dttατ=− , (10.3.58)
we are led to the equations
2
23
d
0
d
k
k
m
ξ
ξ
τρ
′
+=
,
1, 2k
=
,
222
12
ρξξ
=
+
(10.3.58')
if we notice that
2
33
2
dd
d
(1 ) (1 )
dd
d
kk
tt
tt
ξξ
αα
τ
⎡⎤
−−=
⎢⎥
⎣⎦
;
we see that the equations (10.3.58') are of the same form as the equations (10.3.53').
Consequently, we can replace the study of the particle
P of variable mass ()mmt= ,
in the plane
12
Ox x , by the study of a particle Π of constant mass constm
′
= in the
plane
12
Oξξ ; the particle Π is the image of the particle P . Multiplying the equation
(10.3.58') by
d/d
k
ξτ, summing with respect to k and integrating, we get the first
integral of energy for the image particle
22
12
dd
22
dd
m
h
ξξ
ττρ
′
⎛⎞⎛⎞
+=+
⎜⎟⎜⎟
⎝⎠⎝⎠
, (10.3.59)
where
h is an integration constant (the energy constant).
We can make also a direct study of the system of equations (10.3.57'). Taking into
account (10.3.58), we may write the first integral (10.3.59) in the form
(
)
22 2 22
12 1122
(1 ) 4 (1 )( ) 4tx x txxxx rααα α−++−++
2
2(1 )
2
mt
h
r
α
′
−
=+
. (10.3.60)
Multiplying the equation (10.3.57') by
j
x , making successively 1k = ,
2j =
and
2k = , 1j
=
, and subtracting, it results
12 12 12 12
d
(1 ) ( ) ( )
d
t xxxx xxxx
t
αα−−=−− ,
wherefrom (we choose conveniently the integration constant)
12 12
(1 )
C
xx xx t
m
α−=−
, constC
=
; (10.3.60')
we obtain this result also if we make
0λ
=
in the relation (10.3.27') and express the
areal velocity in Cartesian co-ordinates (if
=
u0, then the condition λ=uv, ≠v0,
leads to
0λ
=
). We obtain thus two first integrals, which make easier the integration
of the system of equations (10.3.57').

MECHANICAL SYSTEMS, CLASSICAL MODELS
688
Integrating the third relation (10.3.58) and using the condition
0τ
=
for 0t = (the
same origin on the time-axis both for the particle and its image), we get
2
//1(1 ) 1 2tταα=−−
⎡⎤
⎣⎦
, wherefrom (1/2, )τ
∈
−∞, corresponding ( (,1/)t α∈−∞ )
(
)
11
1
12
t
α
ατ
=−
+
. (10.3.61)
From (10.3.58), it results that, at the initial moment, the particle
P coincides with its
image
Π ; at a certain moment τ (to which corresponds t by the relation (10.3.61)),
the straight line which connects the particle
P to its image Π passes through the
centre of attraction
O . As well, we notice that
2
(1 )
12
rt
ρ
αρ
ατ
=− =
+
. (10.3.61')
Figure 10.25. Motion of a particle
P
of variable mass in a field of central forces.
Elliptical (a) and parabolical (b) trajectory of the image II.
Using the results obtained in Chap. 9, Subsec. 2.1.2, we can state that the image
Π
describes an ellipse, a parabola or a hyperbola as
0h
<
, 0h
=
or 0h > , respectively.
Let us assume that the trajectory of the image
Π is an ellipse, travelled through,
beginning from the point
00
PΠ
≡
(at the moment 0tτ
=
= ), in a period equal to T ;
at the moment
τ , the image of the particle is at Π , while the particle is at P , with
r ρ< (Fig.10.25,a). After a period T , the image of the particle will coincide
with
0
Π , while the particle reaches the location
1
P of radius vector
2
0
11
(1 )rr tα=−
0
/(1 )rTα=+,
0
00
rOP ρ==, at the moment
(
)
1
11/12 /tTαα=− +
. Further, in its motion along the elliptical trajectory, the
particle starts from the position
1n
P
−
and reaches the position
n
P in an interval of time
1
11 1
12
12( 1)
n
n
tt
nT
nT
α
α
α
−
⎡
⎤
−= −
⎢
⎥
+
+−
⎣
⎦
, (10.3.62)

Other considerations on particle dynamics
689
and the distance
1
n
n
PP
−
is given by
[]
0
11
2
(1 2 ) 1 2( 1)
nn
nn
Tr
PP r r
nT n T
α
αα
−−
=−=
++−
. (10.3.62')
It is easy to see that the particle
P approaches the centre of attraction O along a spiral,
the motion being periodical and asymptotically damped towards this centre; the
distance between two successive turns becomes smaller in an interval of time which
becomes smaller too.
If the trajectory of the image
Π is an arc of parabola, then the motion starts from the
point
00
P Π
≡
for which
00
r ρ
=
and, while the image Π describes the arc of
parabola till the point
Π
∞
(τ →∞ and 1/ 0t α→−), the particle P reaches the
centre
O , the tangent to the trajectory passing through Π
∞
(Fig.10.25,b). For
1/2 0τα→− + we have t →−∞; the image Π will tend to the position
lim
Π ,
while the particle
P tends to P
∞
along a curve which meets the straight line
lim
OΠ at
the very same point. In fact, we can assume that the motion starts at
P and tends to O ;
thus, the motion of the particle is aperiodic and strongly damped.
The case in which the image
Π of the particle describes a branch of hyperbola leads
to an analogous result.
3.4 Applications of Meshcherskiĭ’s generalized equation
In some important problems for technics, in which the variation of mass takes place
both by emission and capture, one must use Meshcherskiĭ’s generalized equation in the
form (10.3.8')-(10.3.9'); in what follows, we consider the motion of the aircraft with jet
propulsion as well as the motion of a propelled ship.
3.4.1 Motion of an aircraft with jet propulsion
The displacement of an aircraft with jet propulsion takes place by capture of the air
and then by eliminating it. To study the motion of such an aircraft modelled as a
particle of variable mass, we assume that: i) the change of location of the mass centre of
the aircraft with respect to its case, due to the fuel consumption, is negligible; ii) one
neglects the motion of the air masses in the interior of the aircraft; iii) the relative
velocities of the captured and emitted masses are considered to be collinear with the
velocity of the mass centre of the aircraft. In this case, the motion is rectilinear, along
the
Ox -axis, and the equation (10.3.8) reads
mv F m w m v
−
+
−
=− −
, 0m
−
<
, 0m
+
> , (10.3.63)
assuming that the relative velocity of the emitted masses is constant (
const
−
=
J
JJJJG
w ) and
is directed opposite to the motion, and that the absolute velocity of the captured masses
vanishes (
+
=u0). In technics, it is considered that the rates of flow of capture and
emission are constant, verifying the relation
mmγ
−
+
=
−, where
1γ ≥
characterizes
the variation of mass due to the combustion of the mixture fuel-air; the equation
(10.3.63) becomes (we denote
ww
−
=
)

MECHANICAL SYSTEMS, CLASSICAL MODELS
690
2
0
v
mv m k v m w
γ
−
⎛⎞
=− − −
⎜⎟
⎝⎠
, (10.3.63')
where we assumed that the resistance of the air is proportional to the velocity, in a
horizontal flight. Taking into account the above hypotheses, we may take
0
mmα
−
=− ,
0
/mmαγ
+
= , so that, taking into account (10.3.11) too, it results
0
(1 )mm tλ=−,
1
10
λα
γ
⎛⎞
=
−>
⎜⎟
⎝⎠
. (10.3.64)
The equation of motion reads
(1 )tv w vλασ−=−
,
2
k
α
σ
λ
=
+ , (10.3.63'')
wherefrom, with the initial condition
0
(0)vv
=
, it results
(
)
/
0
() (1 )
ww
vt v t
σλ
αα
λ
σσ
=− − − ; (10.3.65)
observing that
/1σλ , and 11tλ
−
< , we obtain the limit velocity
lim
2
ww
v
k
αγα
σ
αγ
==
+
. (10.3.65')
Integrating with respect to time and using the initial condition
(0) 0x = , we may
write
0
()/
() (1 ) 1
()
wv
w
xt t t
λσ λ
ασ
α
λ
σλσλσ
+
−
⎡
⎤=+ − −
⎣
⎦
+
. (10.3.66)
The length of the active segment of a line is thus determined.
3.4.2 Motion of a propelled ship
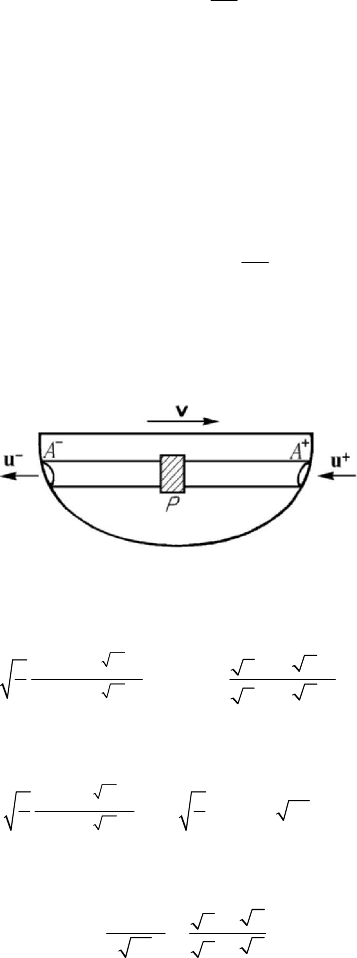
Analogously, we can study the motion of a propelled ship which has a displacement
by absorption of water at its prow with the aid of a pump
P and by elimination of it
with a great velocity at its poop (Fig.10.26). If we put the pump to work and if we
neglect the mass of the consumed fuel, then we may assume that the mass of the ship
remains practically equal to
0
m , so that it can be modelled as a particle of variable
mass, for which the instantaneous variation of the captured mass is equal to the
instantaneous variation of the emitted mass. We consider that the pipe through which
circulates the water is horizontal and that at the initial moment
0t
=
the velocity of the
ship is
0
vw
+
<
; we study the motion of the ship in the interval of time in which its
velocity increases from
0
v to w
+
. If the water is absorbed through a section of area
Other considerations on particle dynamics
691
A
+
and is eliminated through a section of area A
−
, then the flux is the same
(
wA wA
+−
−
+
= ), wherefrom
wwσ
−
+
=
,
A
A
σ
+
−
= ; (10.3.67)
the mass of water absorbed in a unit of time is thus equal to the mass of water
eliminated in the same interval of time (
mA mAμμ
+
−
−
+
=
). The equation (10.3.10'')
leads to
2
00
()mv mkv wA w wμ
−
−−
+
=− + −
,
wherefrom (we denote
ww
+
=
)
22
vkvqw=− +
,
0
qA
m
μ
+
= ; (10.3.68)
the resistance of the air is considered to be proportional to the square of the velocity.
The velocity of the ship does not decrease (
0v >
) if
0q >
, hence if 1σ > (the area
of the absorption section must be greater than the area of the exit section).
Figure 10.26. Motion of a propelled ship.
By integration, we get
2
2
1e
1e
qkwt
qkwt
qC
vw
k
C
−
−
−
=
+
,
0
0
qw kv
C
qw kv
−
=
+
, (10.3.68')
with the initial condition
0
(0)vv
=
; if
0
0v
=
, then we have ( 1C
=
)
()
2
2
1e
tanh
1e
qkwt
qkwt
qq
vwwqkwt
kk
−
−
−
==
+
. (10.3.69)
In this case, the necessary time for the velocity
v of the ship be equal to w is given by
1
ln
2
qk
T
qkw q k
+
=
−
. (10.3.69')
APPENDIX
The appendix contains elements of vector calculus, as well as notions on the field
theory and on the theory of distributions. These results are presented without
demonstration or with a concise one, representing a review of known results or
complements of such results.
1. Elements of vector calculus
In the following, we deal with vector analysis and with exterior differential calculus;
the notions of vector calculus can be found in several chapters of the work and are
linked – especially – to the systems of forces. For a better understanding of the
principal properties of the vectors and taking into account that we apply techniques of
vector calculus to the study of mechanical systems in an Euclidean three-dimensional
space
3
E , we consider the vectors in the vector three-dimensional space
3
L , introduced
in Chap. 1, Subsec. 1.1.2, using oriented segments of line as geometric representations
of them; their tensor properties have been emphasized in Chap. 3, Subsecs 1.2.2 and
1.2.3. However, some results which will be given hold in a n-dimensional vector space
n
L too.
1.1 Vector analysis
A free, bound or sliding vector is a function of the independent variable
[
]
0
1
,ttt∈
if the parameters which determine it are functions of this variable. In general, we
suppose that we have to do with free vectors; however, the results obtained are valid
also for the other types of vectors, excepting special cases. Let be the vector
()t=VV , ()
ii
VVt
=
, 1, 2, 3i
=
, (A.1.1)
with respect to an orthonormed frame of reference; thus, various operations which will
be defined in connection with the vector
V correspond to operations effected on its
components in a system of orthogonal Cartesian co-ordinates or – eventually – in
another system of co-ordinates. In the following, we deal with functions or vector
mappings
()tt→ V , in the mentioned case, in which a single variable is involved, as
well as in the case in which they depend on several variables. Without many details, the
results known for scalar functions may be adapted for vector ones.
693
