Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics
Подождите немного. Документ загружается.

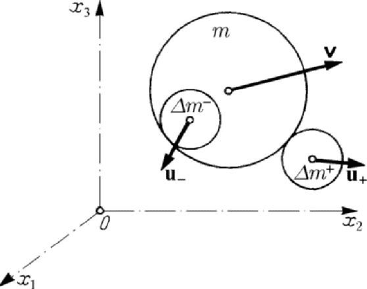
Other considerations on particle dynamics
663
(the captured particles of air are evacuated together with the products of the combustion
in the motor), the jet-propelled ships, the captive balloons (the ballast is thrown and the
connecting cable is lengthened) etc., which can be modelled as particles of variable
mass. Assuming that, in the interval of time
t
Δ
, the particle P loses (emits) a mass
m
−
−Δ , which has the absolute velocity
−
u , and captures a mass m
+
Δ
, which has an
absolute velocity
+
u , using the results previously obtained and the principle of the
parallelogram, we can develop a unitary theory, writing the Meshcherskiĭ generalized
equation in the form (Fig.10.20)
Figure 10.20. Mathematical model for Meshcherskiĭ’s generalized equation.
()()mm m
−+
−
+
=+ − + −
vF u v u v, 0m
−
<
, 0m
+
> . (10.3.8)
Introducing the reactive force (in general, it accelerates the motion of the particle,
especially if its direction is close to that of the velocity
v
)
()mm
−
−
−− −
=−=Ruvw, 0m
−
<
, (10.3.9)
due to the process of emission, and the braking force (in general, it brakes the motion of
the particle, especially if its direction is close to the direction of the velocity
v )
()mm
+
+
++ +
=−=Ruvw, 0m
+
> , (10.3.9')
due to the process of capture, we may write the equation (10.3.8) in the form
m
−
+
=
++
vFR R. (10.3.8')
We notice that, in general, the processes of emission and capture are independent one of
the other and independent of the mass
()mt of the particle
P
. In the case in which the
particle is not free, being subjected to constraints, the corresponding constraint forces
must intervene.
In particular, if only a process of emission takes place, then we obtain
m
−
=
+
vFR, (10.3.10)

MECHANICAL SYSTEMS, CLASSICAL MODELS
664
while in case of only a process of capture, we have
m
+
=
+
vFR
; (10.3.10')
in both equations intervenes an instantaneous variation of mass, which can be
independent of the mass
()mt . If the instantaneous variation of the captured mass is
equal to the instantaneous variation of the emitted mass (
mm
−
+
−
= ), it results
()mm
−
−
+
=
+−
vF u u, (10.3.10'')
where the difference of velocities between the parentheses corresponds, in fact, to a
relative velocity. We notice that the mass
m of the particle at the moment t is given
by
0
mm m m
+
−
=++, 0m
+
> , 0m
−
<
; (10.3.11)
in case of a process of emission, we have
0m
+
=
, so that
0
mm m
−
=+ and
mm
−
=, 0m < , while in case of a process of capture 0m
−
= , hence
0
mm m
+
=+, mm
+
=, 0m > . Thus, we can write the equation (10.3.10'') in the
form
()mm
−
+
=
+−
vF u u, (10.3.10''')
obtaining an equation of the form (10.3.1).
The equations of motion established above, in the frame of the Newtonian model of
mechanics, can be used if a law of variation of mass as function of time is given, in
general of the form
0
()mmft
=
, (0) 1
f
=
, (10.3.11')
0
m being the initial mass at the moment 0t
=
(considered to be the beginning of the
process of mass variation). We mention – especially – the case in which
()
f
t is a
linear function and the reactive force is constant
() 1
f
ttα=− ,
0
Rmwmwα
=
−= , constα
=
, (10.3.12)
and the case in which
()
f
t is an exponential function, the relative acceleration being
constant and the reactive force variable
() e
t
f
t
α−
= ,
1 m
Rww
mm
α=− =
,
0
e
t
Rmw
α
α
−
= ,
constα
=
. (10.3.12')
Reciprocally, if the relative acceleration
/Rm is constant, then the law of variation of
mass is exponential and if, instead the sign – we take the sign + in the formulae
(10.3.12), (10.3.12'), then one obtains the results corresponding to the phenomenon of
capture.

Other considerations on particle dynamics
665
3.1.3 Inverse problem of dynamics of the particle of variable mass
In the direct problem (the first fundamental problem) of a free particle of variable
mass, the given and the reactive force, as well as the braking force (hence, the law of
mass variation) which act upon the particle are given, and one must determine its
trajectory. In the inverse problem (the second fundamental problem), the motion of the
particle is known and the law of mass variation is given and one must determine the
forces which act upon the particle, or the forces which act upon the particle are given
and the law of mass variation must be determined. Obviously, one can imagine various
types of mixed problems.
Let us consider, e.g., the motion of a heavy particle of variable mass along the local
vertical, in a resistent medium; choosing the ascendent vertical as axis, we can write
Meshcherskiĭ’s equation in the form
0
()mv mg m g v mwϕ
=
−− −
,
where
0
()mg vϕ is the resistance of the medium. Taking into account (10.3.11'), we get
f
vgfgfwϕ=− − −
.
Assuming now that the motion of the particle is known, being given by
()xxt= , we
can calculate
()vvt= and than (()) ()vt tϕϕ
=
; observing that ()wwt= and
denoting
()
()
vt g
pt
w
+
=
,
()
()
gt
qt
w
ϕ
=
, (10.3.13)
it results the linear differential equation of first order
() ()() () 0
f
tptftqt
+
+=
, (10.3.13')
which, by integration, reads
()d ()d
() e ()e d
pt t pt t
f
tCqtt
−
∫∫
⎡
⎤
=−
⎣
⎦
∫
, (10.3.13'')
the law of mass variation being thus determined. First of all, let us suppose that the
motion is in vacuum (
() 0vϕ
=
). If
0
constvv
=
= , then it results
() / constpt g w== and () 0qt
=
, while () e
pt
f
tC
−
= ; taking into account
(10.3.11'), we find an exponential law for the mass variation
0
e
g
t
w
mm
−
=
. (10.3.14)
If
00
vatv=+,
0
va=
, then we get, analogously,
MECHANICAL SYSTEMS, CLASSICAL MODELS
666
0
0
e
ag
t
w
mm
+
−
= , (10.3.14')
result which is a generalization of the previous one. Let us suppose now that the motion
takes place in a resistent medium, for which
()vkv
γ
ϕ
=
,
constγ =
. If
0
constvv== , then we obtain
0
() consttkv
γ
ϕ ==
and () / constpt g w==,
0
() / constqt kgv w
γ
==; it results, finally,
(
)
()
000
000
e1 1e 1 e
gg g
tt t
ww w
mm kv m kv mkv
γγγ
−−
⎡⎤
=+−=+−
⎢⎥
⎣⎦
. (10.3.14'')
If
00
vatv=+
,
0
va=
, we get
(
)
00
()tkatv
γ
ϕ
=
+ and
00
00
() e ( ) e d
ag ag
tt
ww
kg
f
tCatvt
w
γ
+
+
−
⎡
⎤
=−+
⎢
⎥
⎣
⎦
∫
;
for
1γ =
(resistance proportional to the velocity) we may write
(
)
{}
0 00
0
00 0
00
e1 1e e
ag ag ag
ttt
www
aw
kg
mm v at
ag ag
+++
−
⎡
⎛⎞ ⎤
=+−−−
⎜⎟
⎢
⎥
++
⎣
⎝⎠ ⎦
0
000
00 00
00 00
1e
ag
t
w
aw mkg aw
kg
mv vat
ag ag ag ag
+
−
⎡⎛ ⎞⎤ ⎛ ⎞
=+ − − − +
⎜⎟ ⎜ ⎟
⎢⎥
++ ++
⎣⎝ ⎠⎦ ⎝ ⎠
.
(10.3.14''')
3.1.4 Motion of a particle of variable mass in absence of given forces.
Tsiolkovskiĭ’s first problem
In absence of given forces, the equation of motion of a free particle
P of variable
mass becomes
mm
=
=
vwR. (10.3.15)
In Tsiolkovskiĭ’s first problem, the relative velocity w , of constant magnitude, is along
the tangent to the trajectory and opposite to the velocity v ; we can thus write
w
mm
v
=−
vv
. (10.3.15')
Let us suppose that the motion is rectilinear, along the
Ox -axis; in a scalar form, we
have
mv mw
=
−
. (10.3.15'')
Taking into account (10.3.11') and integrating with respect to time, we get
lnvwfC=− + ,
constC =
; we obtain Tsiolkovskiĭ’s formula
0
0
ln
m
vv w
m
=+ , (10.3.16)

Other considerations on particle dynamics
667
with the initial condition
0
(0)vv
=
. Let us take a zero initial condition (
0
0v = ) and
let
0
mm= be the total mass emitted till the moment t ; introducing Tsiolkovskiĭ’s
number
0
()/Zmmm
=
− , we may write the velocity at a given moment in the form
ln(1 ) 2.3 log(1 )vw Z w Z=+≅ +. (10.3.16')
This formula allows to obtain some conclusions particularly important in practice.
Thus, the velocity of the particle of variable mass at the end of the active segment (the
end of the process of emission, hence of the combustion in a rocket) is as greater as the
relative velocity of emission is greater; this velocity increases logarithmically with
Tsiolkovskiĭ’s number (in fact, with the ratio of the mass at the initial moment to the
mass at the final moment) and does not depend on the variation law of mass (it does not
depend on the régime of work of rocket’s motor). Hence, to obtain velocities as great as
possible of the particle of variable mass at the end of the process of emission, it is more
advantageous to increase the relative velocity of the evacuated masses than to increase
Z (the reserve of fuel). The motor of the rocket must be improved and the fuel must be
conveniently chosen.
If the relative velocity (of emission) changes of direction, remaining constant in
modulus (reactive braking), when the particle
P reaches the velocity
1
v , then is put the
problem to determine the supplementary reserve of mass, necessary to equate to zero its
velocity
2
v (for the landing of the rocket). Let us suppose that at the velocity
0
11
ln( / )vwmm= the mass of the particle is
1
m ; we can write
1
21
2
ln 0
m
vvw
m
=
−=,
where
2
m is the mass of the particle which corresponds to
2
0v = . It results
0
112
//mm mm
=
or
()
2
0
212
//mm mm= . If
122
()/Zmmm
′
=
− is
Tsiolkovskiĭ’s number which defines the total reserve of mass, then we can write
2
1(1)ZZ
′
+=+ , wherefrom
(2)ZZZ
′
′
=
+ ; (10.3.17)
we obtain thus the total reserve of mass necessary to landing as function of
Tsiolkovskiĭ’s number at the end of the driving line segment.
Observing that
d/dvxt= , starting from (10.3.16), and taking into account
(10.3.11'), we can write
00
0
ln ( )d
t
xx vtw fττ=+ −
∫
. (10.3.18)
In the particular case in which the relative velocity of emission vanishes (
0w = ), it
results a uniform motion (
00
xx vt
=
+ ). If the mass has a linear variation of the form
(10.3.12), then we get

MECHANICAL SYSTEMS, CLASSICAL MODELS
668
[]
00
(1 )ln(1 )
w
xx vt t t t
ααα
α
=+ + − − + , (10.3.18')
while if the mass has an exponential variation of the form (10.3.12'), then we obtain
2
00
1
2
xx vt wtα=+ + ; (10.3.18'')
the parameter
α is called unit mass of consumption and characterizes the consumption
of mass with respect to the initial mass. In the first case, the reactive force is constant
and is given by (10.3.12), while in the second case the relative acceleration of emission
is constant and the reactive force has an exponential variation, being given by
(10.3.12').
3.1.5 Theorem of momentum
Starting from Meshcherskiĭ’s equation (10.3.1), we can extend the general theorems
of mechanics to the dynamics of the free particle of variable mass; we mention that the
generalized Meshcherskiĭ equation does no more lead to interesting results.
The equation of motion (10.3.1) leads to the formula (10.3.1') or to the formula
(10.3.3) and we may state (with respect to an inertial frame of reference)
Theorem 10.3.4 (theorem of momentum). The derivative with respect to time of the
momentum of a free particle of variable mass
()mmt
=
is equal to the sum of the
resultant of the given forces which act upon the particle and the product of the
derivative with respect to time
m of the mass of the particle, which characterizes its
variation, by the absolute velocity of the emitted or captured mass (
0m < corresponds
to the phenomenon of emission, while
0m > corresponds to the phenomenon of
capture).
We notice that the product
m u is of the nature of a force (different from the reactive
force definite by the relation (10.3.2)).
By integration with respect to time, for
[
]
12
,ttt
∈
, we obtain
22
11
212211
() () ()d ()()d
tt
tt
t t m m tt mt ttΔ= − = − = +
∫∫
HH H v v F u
22
11
()d ()d ()
tm
tm
tt tmt=+
∫∫
Fu (10.3.19)
and may thus state
Theorem 10.3.5 (theorem of variation of momentum). The variation of the momentum
of a free particle of variable mass in a given interval of time is equal to the sum of the
impulse of the resultant of the given forces which act upon it and the impulse of the
mass emitted or captured in the same interval of time.
If the absolute velocity of the emitted or captured masses vanishes (
=u0), then we
find again the Theorem 10.3.2, and the formula (10.3.19) is reduced to the formula
(6.1.45'').
If the absolute velocity u is constant in time (
0
=
uu), then we get

Other considerations on particle dynamics
669
2
1
22 11
()d
t
t
mm tt−=−
∫
ww F,
0
11
=
−wuv,
0
22
=
−wuv, (10.3.19')
where we have introduced the relative velocities
w
at the initial and at the final
moment, respectively.
If the relative velocity w vanishes (
=
uv), then we may write
22
11
22 11
()d ()d ()
tm
tm
m m tt tmtΔ= − = +
∫∫
Hv v F v . (10.3.19'')
In the case in which the resultant of the given forces vanishes (
=F0) the formula
(6.1.45'') leads to a conservation theorem of momentum (
11 22
mm
=
vv); assuming that
the initial moment is
1
0t = , while the final moment is t , we may write
0
00
1
()
()
m
t
mft
==vvv
(10.3.20)
too, the velocity being of constant direction. In general, we can write a scalar first
integral if the projection (component) of the sum
m
+
Fu along a fixed direction
vanishes; if
m
+
=Fu0, (10.3.21)
then we obtain a conservation theorem of momentum. Let us express the given force in
the form
=Fa, where a is a vector component of the acceleration
v ; the above
condition takes the form
mm
+
=au0. Hence, taking into account (10.3.11''), we can
state
Theorem 10.3.6 (conservation theorem of momentum). The momentum of a free
particle of variable mass is conserved in time if and only if the masses emitted or
captured are moving after a law given by the relation
()tλ=ua,
1
()
(d/d )ln
t
tf
λ =−
. (10.3.21')
In fact, integrating once more, we get a new vector first integral, corresponding to
the motion law of the particle.
From the formula (6.1.45''), we obtain
0
21 21
()mm tt
−
=−vvF (10.3.22)
if
0
const==
J
JJJJG
FF
.
3.1.6 Theorem of moment of momentum. Theorem of areas
Starting from the relation (10.3.1') or from the relation (10.3.3) and by means of a
vector product at left by
r , we get

MECHANICAL SYSTEMS, CLASSICAL MODELS
670
[]
d
() ()
d
OO
mm
t
×==+×
rvKMru
,
O
=
×MrF (10.3.23)
and we state
Theorem 10.3.7 (theorem of moment of momentum). The derivative with respect to
time of the moment of momentum of a free particle of variable mass, with respect to a
given pole, is equal to the sum of the moment of the resultant of the given forces which
act upon it and the moment of the product of the derivative with respect to time of the
mass of the particle, which characterizes its variation, by the absolute velocity of the
mass emitted or captured, with respect to the same pole.
By integration with respect to time, for
[
]
12
,ttt
∈
, we get
21222111
() () ( ) ( )
OO O
tt m mΔ= − =× −×KK K r vr v
22
11
()d () ()d ()
tm
O
tm
tt t tmt=+×
∫∫
Mru. (10.3.24)
If the absolute velocity of the masses emitted or captured vanishes (
=u0), then this
formula is reduced to the formula (6.1.46'') and we can state
Theorem 10.3.8. If the absolute velocity of the emitted or captured masses by a free
particle of variable mass vanishes, then we may express the theorem of moment of
momentum as in the case of a particle of constant mass.
If the moment of the resultant of given forces vanishes (
O
=
M0) too, then we
obtain a conservation theorem of the moment of momentum (
22 2 11 1
mm
×
=×rv rv).
Assuming that the initial moment is
1
0t
=
, while the final one is t , and introducing
the areal velocity given by (5.1.16), we may also write
0
00
1
()
()
m
t
mft
==
Ω
ΩΩ; (10.3.25)
hence, the areal velocity is of constant direction. In general, we obtain a scalar first
integral if the projection (component) of the sum
()
O
m
+
× Mr u on a fixed direction
vanishes. If
()m×+ =rF u 0, then we obtain a conservation theorem of moment of
momentum. We notice that, if a relation of the form (10.3.21) takes place, then we can
write not only a conservation theorem of momentum, but a conservation theorem of
moment of momentum (
const
O
==
J
JJJJG
KC ) too. As in the case of the particle of
constant mass, the trajectory of the particle
P of variable mass is plane and it results
1
2m
=
CΩ . (10.3.26)
Because
()mmt= , we can no more write a theorem of areas. We may state
Theorem 10.3.9. To conserve the moment of momentum of a free particle of variable
mass, it is sufficient that the emitted or captured masses move after a law given by the
relation (10.3.21').

Other considerations on particle dynamics
671
The relation (10.3.23) may be written also in the form
d
() ( )2 ( )
d
mm m m
t
×= ×==×+×
rv rv rFrwΩ
. (10.3.26')
We have
const ( ) ( )m=⇔×+×=×+=
J
JJJJG
rFr w r F R 0Ω
;
hence, we can state
Theorem 10.3.10 (conservation theorem of areal velocity). In case of a free particle of
variable mass, the areal velocity with respect to a given pole is conserved only and only
if the sum of the moment of the resultant of the given forces which act upon the particle
and the moment of the product of the derivative with respect to time of the particle
mass, which characterizes its variation by the relative velocity (with respect to the
particle) of the emitted or captured mass, with respect to the same pole, vanishes.
We can mention some particular cases in which a conservation theorem of areal
velocity takes place, hence a theorem of areas too. Thus, if the resultant
F
of the given
forces is a central one, passing through the pole
O
, and if the support of the relative
velocity
=−wuv passes through the same pole, then it results const=
J
JJJJG
Ω
; in
particular, we can have
=
w0 (hence,
=
uv) or
=
F0. One obtains the same result
if the resultant
F of the given forces equilibrates the reactive force R .
In the case in which the absolute velocity u of the emitted and captured masses is
collinear with the velocity
v
of the particle P of variable mass ( λ
=
uv), ()tλλ= ,
the force
F being a central one, we may write the theorem of moment of momentum in
the form
d
() ()
d
mm
t
λ×=×rv r v;
introducing the areal velocity, we find
(1)
m
m
λ=−
Ω
Ω .
Because
Ω
and dΩ are collinear vectors, it results that ()t
Ω
and (d)tt+Ω are
collinear vectors at any moment
t , the areal velocity
Ω
being thus a vector of constant
direction; hence, the trajectory of the particle
P is a curve contained in a plane which
passes through the fixed pole
O . A scalar product of the relation obtained above by Ω
leads to (we notice that ΩΩ⋅=
ΩΩ )
(1)
m
m
Ωλ Ω=−
;
denoting
Ω= u
Ω
, vers=u
Ω
, we can write ΩΩ=+
uuΩ , wherefrom, taking into
account the above relations, we get
=
u0 or const=
J
JJJJG
u , hence the same conclusion as
above. Integrating and using polar co-ordinates in the plane of motion, we have

MECHANICAL SYSTEMS, CLASSICAL MODELS
672
d
(1)
2
2e
m
m
rC
λ
Ωθ
−
∫
=
=
. (10.3.27)
If
constλ = , then it results
21
2 rCm
λ
Ωθ
−
=
=
; (10.3.27')
for
1λ = we find again the previous result, in which the areal velocity is conserved.
This case is encountered in the external ballistics of the particle of variable mass.
As in the particular case of constant mass, the Theorems 10.3.4 and 10.3.7 allow us
to write
() () ( )
OOO
mτ=τ+τ
HF u (10.3.28)
and to state
Theorem 10.3.11 (theorem of torsor). The derivative with respect to time of the torsor
of a free particle of variable mass, with respect to a given pole, is equal to the sum of
the torsor of the resultant of the given forces which act upon it and the torsor of the
product of the derivative with respect to time of the particle mass, which characterizes
its variation, by the absolute velocity of the emitted or captured mass, with respect to
the same pole.
Obviously, the condition (10.3.21) leads to a conservation theorem of torsor.
Starting from (10.3.1'') and (10.3.26'), we may write
() () ()
OOO
mτ=τ+τ
vFR, (10.3.28')
where
R is the reactive force.
3.1.7 Theorem of kinetic energy
Starting from Meshcherskiĭ’s relation (10.3.1) or (10.3.3') and with the aid of a scalar
product by
ddt=rv, we can write
2
dd d dmvm m⋅+ =⋅+⋅vv Fruv
;
introducing the kinetic energy
2
/2Tmv=
and the elementary work of the given
forces
ddW =⋅Fr, it results
2
1
ddd d
2
TvmWm
+
=+⋅ ur, (10.3.29)
so that we may state
Theorem 10.3.12 (theorem of kinetic energy). The sum of the differential of the kinetic
energy and the semiproduct of the differential of mass by the square of the velocity of a
free particle of variable mass is equal to the sum of the elementary work of the resultant
of the given forces which act upon the particle and the elementary work of the product
of the derivative with respect to time of the particle mass, which characterizes its
variation, by the absolute velocity of the emitted or captured mass.
