Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

xii

Passing by non-significant details, one presents some applications connected to

important phenomena of nature, and this also gives one the possibility to solve

problems of interest from the technical, engineering point of view. In this form, the

book becomes – we dare say – a unique outline of the literature in the field; the author

wishes to present the most important aspects connected with the study of mechanical

systems, mechanics being regarded as a science of nature, as well as its links to other

sciences of nature. Implications in technical sciences are not neglected.

Starting from the particle (the simplest problem) and finishing with the study of

dynamical systems (including bifurcation, catastrophes and chaos), the book covers a

wide number of problems (classical or new ones), as one can see from its contents. It is

divided in three volumes, i.e.: I. Particle mechanics. II. Mechanics of discrete and

continuous systems. III. Analytical mechanics.

The book uses the known literature, as well as the original results of the author and

his more than fifty years experience as a Professor of Mechanics at the University of

Bucharest. It is devoted to a large circle of readers: mathematicians (especially those

involved in applied mathematics), physicists (particularly those interested in mechanics

and its connections), chemists, biologists, astronomers, engineers of various specialities

(civil, mechanical engineers etc., who are scientific researchers or designers), students

in various domains etc.

7 January 2006

P.P. Teodorescu

Chapter 1

NEWTONIAN MODEL OF MECHANICS

The mathematical models of mechanics, the first basic science of nature, are shortly

presented in this chapter; stress is put on the notion of mechanical system.

Considerations concerning the units are made and some results concerning the theory of

homogeneity and similitude are given. Using these introductory notions, one can pass to

a mathematical study of the mechanical systems.

1. Mechanics, science of nature. Mechanical systems

All the phenomena of nature are characterized by motion; this is an essential property

of matter, having infinity of aspects. For instance, the motion can be mechanical,

physical, chemical and biological; there correspond various sciences of nature. Among

them, mechanics studies the objective laws of the mechanical motion of material bodies,

the simplest form of motion of matter; we will deal with such a study in what follows.

The scientific study of matter has put in evidence its existence in the form of physical

systems. The simplest physical system is the substance, which is met in nature in the

form of material body; we will consider these bodies in their real form, as well as in

their idealized form of discrete systems of particles (atoms, molecules, usual bodies,

planets etc.) or of continuous systems (solids, fluids), under the denomination of

mechanical systems.

Mathematics plays a very important rôle in the study of a science of nature.

Mechanics has been the first science of nature which was strongly mathematicized, by

considering various mathematical models, which have been proved to correspond to the

surrounding reality. To mechanical systems there correspond thus mathematical models

of organized matter, having certain properties of structure, form etc. The development

of mechanics has been thus much influenced by the use of a strong mathematical tool;

as a matter of fact, we observe that mechanics also played an important rôle in the

introduction and development of many mathematical notions.

1.1 Basic notions

Introducing the notions of system and mathematical model, we consider the main

systems and models of such kind used in mechanics; we put thus in evidence the

hypotheses that are introduced and the basic notions which appear. The object of study

of mechanics is thus emphasized. We must point out that the notions which will be

introduced are basic notions; these ones cannot be defined with the aid of other notions,

and they must be described by their various properties, obtaining thus the considered

mathematical models.

MECHANICAL SYSTEMS, CLASSICAL MODELS

1.1.1 Notion of system. Notion of mathematical model

In the study of a science of nature, more and more the connection between the

modern methods of the theory of systems and the mathematical modelling of this

science is put into evidence. One must first of all lighten the notion of system, which

may be different from that suggested by the usual language; on the other hand, this

notion must be used always when one has to do with complicated phenomena, the

search of which is proved to be difficult. At the same time, one must take into

consideration the possibility of coupling characteristic phenomena from various

sciences of nature (mechanics, physics, chemistry, biology etc.).

A system is defined by a set of elements (component parts), which influence

(condition) each other (which interact), on which external influences (actions,

denominated input) take place, and the actions of which towards the exterior (towards

other systems) are denominated output. One obtains thus the schema

Input

⎯

⎯⎯⎯→

Output

⎯

⎯⎯⎯→

Among the most important properties of a system we must mention its change

(transformation, motion), as well as the possibility to be influenced (conducted) by a

convenient choice of the inputs (forces). In classical mechanics, the connection between

the influences (actions) exerted on the system and the changes of the latter one is called

dynamics of systems. It is understood that these considerations refer first to mechanical

systems; but, in general, taking into account the connection between various systems,

dynamics of systems is an interdisciplinary science.

To study these systems, following problems are put: i) the construction of the

mathematical model corresponding to a given system; ii) the study of the model thus

created (putting into evidence the properties of the system); sometimes, because of the

difficulties of the considered problems, one cannot give a complete solution to the

problem of motion and one emphasizes only some of its properties or one can give only

approximate solutions (e.g., by linearizing non-linear phenomena); iii) the choice of the

main (dominant) inputs, which govern the considered phenomena; iv) the simulation of

the behaviour of the considered system; one can thus put in evidence the deficiencies of

the chosen model as well as of the considered inputs, improving then the model and the

inputs. We will deal particularly with the first two problems in our study, accidentally

with the third one and less with the fourth one.

Usually, by model we understand an object or a device artificially created by men,

which is similar in a certain measure with another one, the latter being an object of

search or of practical interest. The scientific notion of model constitutes a possibility of

knowledge of the surrounding reality, consisting in the representation of the

phenomenon to be studied with the aid of a system artificially created. Hence, the most

general property of a model is its capacity to reflect, to reproduce things and phenomena

of the objective world, their necessary order and their structure.

From the very beginning, the models can be divided in two great classes: technical

(material) models and ideal (imaginary) models; this classification is made considering

the construction of the models as well as the possibilities by which the objects to be

studied may be reproduced.

Set of elements in

continuous

Newtonian model of mechanics

The technical models are created by man, but they do exist objectively, independent

of his conscience, being materialized in metal, wood, electromagnetic fields a.s.o. Their

destination is to reproduce for a cognitive goal the object to be studied, to put in

evidence its structure or certain of its properties. The model can maintain or not the

physical nature of the object which is studied or the geometrical similitude to this one.

If the similitude is maintained, but the model differs by its physical nature, we have to

do with analogic systems. E.g., electrical models may reproduce processes analogous to

those encountered in mechanics, qualitatively different, but described by similar

equations. These models, as others of the same kind, take part in the class of

mathematical models.

One can construct such models, for instance, to study the torsion of a cylindrical

straight bar of arbitrary simply or multiply connected cross section. If the bar is

isotropic, homogeneous and linear elastic (subjected to infinitesimal deformations), then

the phenomenon is governed by a Poisson type equation in B. de Saint-Venant’s theory.

L. Prandtl showed that the same partial differential equation is met in case of a

membrane which rests on a given contour and is subjected to an interior constant

pressure; if this contour is similar to the frontier of the plane domain corresponding to

the cross section of the straight bar, then we obtain a correspondence of the boundary

conditions, hence the classical membrane analogy (or of the soap film). One uses also

other analogies for the same problem, i.e.: electrical modelling, modelling by optical

interference, hydrodynamical modelling a.s.o.

Another type of technical models used in mechanics corresponds to the intuitive

notion of model. Various elements of construction are performed partially or in totality

at a reduced scale, obtaining thus results concerning the maximal stresses and strains

which appear. These models can be built of the same material as the objects to be

studied or of other materials, so that quite difficult problems of similitude must be

solved.

Generally, the ideal models are not materialized and – sometimes – they neither can

be. From the viewpoint of their form, they can be of two types.

The models of first order are built by using intuitive elements, which have a certain

similitude with the corresponding elements of the real modelled phenomenon; we

observe that this similitude must not be limited only to space relations, but can be

extended also to other aspects of the model and of the object (for instance, the character

of the motion). The intuitiveness of these models is put into evidence first of all by the

fact that the models themselves, formed by elements sensorial perceptible (plates,

levers, tubes, fluids, vortices etc.), are intuitive, and – on the other hand – by the fact

that they are intuitive images of the objects themselves. Sometimes, these models are

fixed in the form of schemata.

The models of second order are systems of signs, their elements being special signs;

logical relations between them form – at the same time – a system, being expressed also

by special signs. In this case, there is no similitude between the elements of the model

and the elements of the corresponding objects. These models do not have intuitiveness

in the sense of a spatial or physical analogy; they have not, by their physical nature,

nothing in common with the nature of the modelled objects. The models of second order

reflect the reality on the basis of their isomorphism with this reality; we suppose a one-

to-one correspondence between each element and each relation of the model. These

models reproduce the objects under study in a simplified form, constituting thus – as all

models – a certain idealization of the reality.

MECHANICAL SYSTEMS, CLASSICAL MODELS

The types of ideal models mentioned above can be considered as limit cases. In fact,

there exist ideal models that have common features to both types of models which have

been described; they contain systems of notions and axioms which characterize

quantitatively and qualitatively the phenomena of nature, for instance representing

mathematical models. Such models are extremely important and their systematic use

has led to the great development of mechanics of deformable bodies in the last time.

The basic dialectical contradiction of the model (the model serves to the knowledge

of the object just because it is not identical with the latter one) is useful, for instance to

put into evidence the properties of continuous deformable media. In fact, a model

contains more information about the object if it is closer to it. But physical reality is

very complicated; the solving of the contradiction is realized by the use of a sequence of

models, more and more complete, each one having its contribution to the knowledge of

the real continuous deformable media. We try to put into evidence just this process of

continuous improvement of the models in general mechanics as well as in mechanics of

continuous deformable media, process that constitutes the main tenor of the

development of mechanical systems.

In general, after adopting a model, it is absolutely necessary to compare the results

obtained by theoretical reasoning to physical reality. If these results are not satisfactory

(sometimes it happens to be between some limits, which can be sufficiently close), then

it is necessary to make corrections or to improve the chosen model. In fact, on this way,

mechanics, the theory of mechanical systems developed itself, the word “model” being

more and more used by researchers dealing with this science of nature.

1.1.2 Vectorial modelling of mechanical quantities. Vector space

A great part of the quantities which appear in mechanics are mathematically

modelled as vector quantities; in fact, the concept of vector appeared together with the

development of mechanics. We will thus introduce the notion of vector space, a space

of mechanical quantities, by considering three types of vectors useful in the study of

mechanical systems, i.e.: free vectors, bound vectors and sliding vectors.

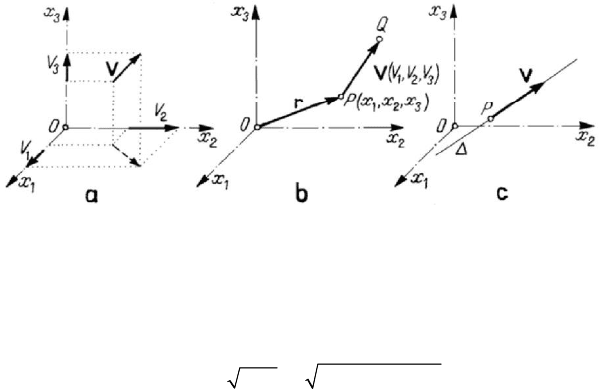
The free vector is a mathematical entity characterized by direction and modulus

(magnitude). The direction includes all straight lines parallel one to each other, as well

as a sign; in case of opposite signs, the directions are opposite. It is denoted by

(sometimes

→



); the modulus of this vector will be

V V

, ≥ 0V (it is

denoted also by

V , and it is called the norm of the vector).

We fix a right-handed frame of reference, formed by an origin

and by three

orthogonal axes

=,1,2,3,

Ox i in the Euclidean three-dimensional space

E . We

mention that by a right-handed frame of reference we understand that one for which an

observer situated along the axis

Ox , in its positive sense, sees the superposition of the

axis

Ox onto the axis

Ox , after a rotation of angle /2π in the positive sense (from

right to left, the right-hand rule); we admit that

(, , ) (1,2,3)ijk ,

(1.1.1)

the indices

,,ijk taking the distinct values 1, 2, 3 in the given order or after a cyclic

permutation of them. Projecting the free vector

V on the axes (we use the definition

Newtonian model of mechanics

that will be given later, in this subsection), we obtain its canonical co-ordinates

=,1,2,3

Vi (Fig.1.1,a); these co-ordinates have a certain sign, as the direction of the

Figure 1.1. Free (a), bound (b) and sliding (c) vectors.

projections coincides or not with the direction of the co-ordinate axes (which are

directed axes), and constitute an ordered triplet of numbers, which entirely characterize

the free vector. We can write

⎛⎞

===++

⎜⎟

⎝⎠

∑

1/2

2222

123

iii

V V VV VVV,

(1.1.2)

where we use Einstein’s convention of summation, in conformity with which the double

existence of an index (called dummy index) in a monomial indicates the summation with

respect to this index. An index, which appears only once, will be a free index; in the

frame of the adopted convention, an index cannot appear three times.

The bound vector is a mathematical entity, characterized by direction, modulus

(magnitude) and point of application (origin). In the frame of reference

123

Ox x x , the

point of application

P (the origin of the vector) is given by the position vector

123

(, , )xxx (which is also a bound vector, the point of application of which is the

origin

); the point Q represents the extremity of the vector (Fig.1.1,b). A bound

vector

V PQ

JJG

is characterized by the bound vector r and the free vector V , hence

by two ordered triplets of numbers (

x and

,1,2,3

Vi ). Thus, PQ

JJG

is a directed

(oriented) segment; we notice that

JJG

is the opposite directed segment.

The sliding vector is a mathematical entity, characterized by direction, modulus

(magnitude) and support (the vector lies on an axis

Δ , without mentioning the point of

application, but having the possibility to slide along this axis). From the mathematical

point of view, a sliding vector will be characterized also by two ordered triplets of

numbers (

x and =,1,2,3

Vi ), between which there exists a certain relation, hence by

five independent numbers (a sixth number is necessary to can have the position of the

point of application

P on the axis Δ , with respect to an origin chosen on it, to obtain a

bound vector) (Fig.1.1,c).

We say that between two vectors

V and W of the same type there exists a relation

of equality if they are characterized by the same elements (direction, modulus, point of

application, support) or the same canonical co-ordinates. For instance, for the free

MECHANICAL SYSTEMS, CLASSICAL MODELS

vectors

(

)

V and

()

W we can write

=VW,

VW,

1, 2, 3i

;

(1.1.3)

for the sliding vectors we must have also the same support, while for the bound vectors

the same point of application. We mention following properties (

V , W and U are

vectors):

VV (reflexivity);

ii)

⇔=VW WV (symmetry);

iii)

VW, =⇒=WU VU (transitivity)

valid for each type of vector.

If we bound two equal free vectors to two distinct points of application, then we

obtain two bound vectors, which are equipollent.

Let be vectors

V and

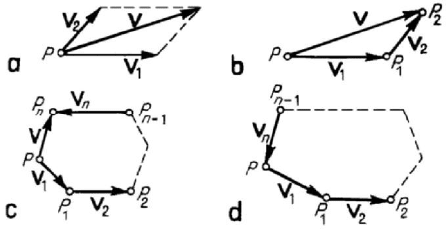
V ; the sum

+VV V

(1.1.4)

is a vector for which the direction and modulus are given by the diagonal of the

parallelogram constructed by means of these vectors, admitting that they are applied at

Figure 1.2. Addition of two vectors (a, b). Addition of n vectors:

non-vanishing resultant (c); vanishing resultant (d).

the same point (Fig.1.2,a). The above given definition corresponds to free vectors, to

bound vectors (if they have the same point of application), as well as for sliding vectors

(if their supports are concurrent). The sum can be obtained also by closing a triangle,

the first two sides of which are

V and

V (Fig.1.2,b); this observation can be used to

construct the sum of

n vectors (Fig.1.2,c)

+++VV V V

... .

(1.1.5)

We can write also Chasles’ relation

−

=+ ++

112 1

...

PP PP P P P P

JJJG JJJG JJJJG JJJJJJJG

(1.1.5')

Newtonian model of mechanics

The resultant

V closes the vectors’ polygon (a skew polygon in

); if this

polygonal line is closing, then the resultant vanishes (Fig.1.2,d). We mention following

properties:

=+VV VV

12 21

(commutativity);

ii)

()

(

)

+=++VVV VVV

123 123

(associativity).

The inequalities

−≤+≤+VV VV VV

12 12 12

≥VV

(1.1.6)

result from Fig.1.2,b.

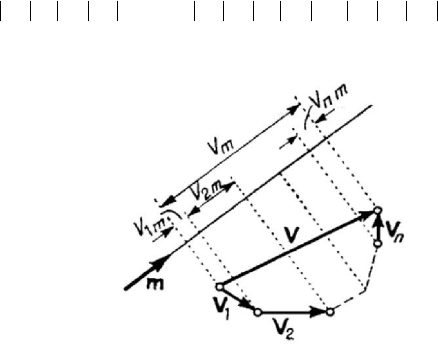
Figure 1.3. Projection of a vector on a directed axis.

Let

V be the projection of vector

V ,

1,2,...,in, on an directed axis, of sliding

vector

m , while

V is the projection of vector V on the same axis (by projection of a

bound vector

JJG

on a directed axis we understand the length of the directed segment

''PQ

JJJG

of this axis, limited by planes normal to the given axis, passing through points P

and

Q ; this length is a positive number if

(

)

<m,/2PQ π

JJG

)

and negative in the

contrary case). We observe that (Fig.1.3)

+++

...

mnm

VV V V;

(1.1.7)

if the vectors’ polygon is closing, then the sum of the projections on an axis vanishes.

Thus, for the sum of two vectors one obtains the canonical co-ordinates

VV V,

1, 2, 3i .

(1.1.8)

We say that vector

V is equal to zero

(1.1.9)

if and only if

MECHANICAL SYSTEMS, CLASSICAL MODELS

= 0

1, 2, 3i , or

;

(1.1.9')

in this case, the properties

=+ =V00V V

(1.1.9'')

are verified.

We observe that the law of internal composition of vectors (addition of vectors,

introduced above) is essential to define them; we must complete the definition given in

this subsection, because there exist quantities which can be represented by directed

segments, but which do not verify such a law of composition, so that they are not

vectors in the sense considered above (for instance, the finite rotation of a rigid solid

about an axis).

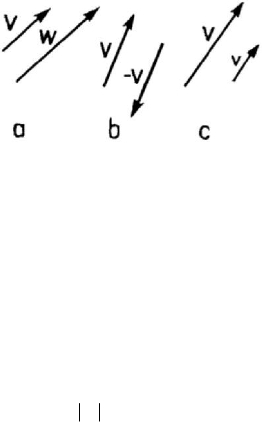
Figure 1.4. The product of a scalar by a vector.

The scalar is a mathematical entity, characterized by sign and modulus (magnitude);

hence, it is a number.

The product of a scalar

λ by a vector V is a vector (Fig.1.4,a)

WVλ ,

(1.1.10)

which has the same direction as

V if > 0λ or an opposite direction if < 0λ , and the

modulus

WVλ

(1.1.10')

In the particular case

−1λ , we obtain the vector

−

V , which has the same

modulus as

V , but an opposite direction (Fig.1.4,b); this vector verifies relation

(

)

−=VV0.

(1.1.11)

As a consequence, the subtraction of two vectors is also an addition

(

)

−

=+−VV V V

12 1 2

(1.1.12)

We mention following properties:

(

)()

==VVV

12 21 12

λλ λλ λλ (associativity);

ii)

()

+=+VV V

12 12

λλ λλ (distributivity with respect to addition of scalars);

iii)

()

+= +VV VV

12 12

λλ λ (distributivity with respect to addition of vectors).

Newtonian model of mechanics

The product (1.1.10) vanishes

(

)

V0λ if and only if

0λ or =V0.

We observe that two vectors

V and W have the same (or an opposite) direction

(they are collinear, even if they have not the same support) if and only if they verify a

relation of the form (1.1.10) or of the form

=VW0λμ ,

≠

,0λμ .

(1.1.13)

Let be a vector

V . We denote by

a vector which has the same direction as V , but

of modulus equal to unity (Fig.1.4,c); this vector is called the unit vector (versor) of

and is denoted by

vVvers .

(1.1.14)

We may write

versVV===VVvVv.

(1.1.14')

The unit vectors of the co-ordinate axes

Ox are denoted by

i ,

1, 2, 3j .

Let be the set of free vectors

{}

V , for which an operation of internal composition

(addition of vectors) is defined, so that the sum of two elements of this set is an element

of the same set; this operation is associative and admits an inverse.

Vector

0 is the neutral element, which verifies relations (1.1.9''), while vector −V is

the inverse of

V , verifying relation (1.1.11); these vectors belong to set

{}

V . Hence,

the set of free vectors

{}

forms an Abelian (commutative) group (the operation of

internal composition of vectors is commutative).

Because in the set

{}

V was defined also the operation of multiplication of one of its

elements by a scalar (external composition), this set constitutes a three-dimensional

vector space (the linear space

L ). Analogously, one can introduce also the n-

dimensional vector space

L .

1.1.3 Space. Time

Space and time are basic notions, which appear in a mathematical model of

mechanics. To study the mechanical motion, representations of space and time are

necessary; so, in classical mechanics, the physical space is the three-dimensional

Euclidean space

E , while time is assimilated also to a Euclidean space, but to a

unidimensional one

. It was thus admitted that material bodies have three dimensions

(e.g., length, width and height); but if the bodies to be studied are reduced to two

dimensions or to only one dimension, so that they may be modelled in such a form, then

we use a two-dimensional Euclidean space

E or a unidimensional one

E ,

respectively. The geometric models for space and time used in classical mechanics

reflect thus properties of real space and time, as objective forms of existence of matter.

In a classical model of mechanics, the space is considered infinite, continuous,

homogeneous, isotropic and absolute, being independent of matter. Material bodies are

immersed into space, where they fill a certain position with respect to other objects of

the material world; they have also a certain extent. One can thus say that the space