Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

()

=+ −

∑

rr rr

() ()

mμμ δ ,

(1.1.71'')

where the sign “tilde” corresponds to

the differentiation in the usual sense,

μ is the

density corresponding to a continuous system,

m are the masses of n particles of

position vectors

r ,

= 1,2,...,in

, while δ is the Dirac distribution.

The density of a particle of mass

m and position vector

r is thus given by

(

)

−rrr

() mμδ ;

(1.1.72)

in the case of a discrete mechanical system we have

()

=−

∑

rrr

()

mμδ,

(1.1.72')

while for a continuous mechanical system we obtain

()

(1.1.72'')

The function

≥r() 0μ is continuous at least partially; in general, if no confusion is

possible, then we omit the sign tilde. Obviously, we can introduce also the notion of

mean density

mean

()

(1.1.72''')

where

Δm is the mass of a finite volume element

V (Fig.1.14); there results

Δ→

mean

() lim ()

μμ.

(1.1.72

)

The mass is given by

dMV

Ω

μ=

∫

(1.1.73)

for an arbitrary mechanical system, the integral being a

Stieltjes integral; in case of a

discrete mechanical system, we have

∑

(1.1.73')

while for a

continuous mechanical system we may write

()d

MVμ=

∫

(1.1.73'')

Newtonian model of mechanics

the integral being a

Riemann integral

(

)

μμ.

In this last case, the density varies from one point to another one, and the continuous

mechanical system is

non-homogeneous; in the case in which the density μ is the same

for all the points of the continuous medium, this one is

homogeneous (besides, in this

case all its mechanical and physical properties are the same in any points) and we may

write

MVμ .

(1.1.73''')

We remark that, in general, the results obtained for a discrete mechanical system may

be enounced also for a continuous mechanical system by replacing the sign

∑

by the

sign

∫

. Thus, two types of mathematical models of mechanics have been put in

evidence, i.e.

the discrete model and the continuous model. We mention that one can

construct also other more sophisticated mathematical models, for example

quasi-

continuous models

(continuous models which take in consideration the discrete

structure of matter); the above general considerations remain valid also in this case. One

can study also mathematical models which start from the discrete character of material

bodies; with the aid of a sufficient great number of particles, they introduce statistical

methods of computation, using

aleatory variables.

1.1.9 The principle of mass conservation

The geometric support of a continuous mechanical system can vary in time

()

= ()VVt. The formula (1.1.73'') is of the form

()

123

()

,,;d

MxxxtVμ=

∫

(1.1.74)

where

()

xxt

= 1, 2, 3j , and

123

ddddVxxx. By a change of variables of the

form

()

000

123

,,;

x xxxxt,

1, 2, 3i ,

(1.1.75)

the Jacobian

J of the transformation being different from zero

()

123

000 0

123

det det 0

xxx

xxx x

⎡⎤

∂

≡≡≠

⎢⎥

∂∂

⎣⎦

(1.1.75')

it follows that

MJVμ=

∫

(1.1.74')

where

()

xxt, = 1, 2, 3j ,

()VVt, =

000

123

d dddV xxx correspond to the

initial moment

t . If we write the formula (1.1.74) for

tt, and if we take into

MECHANICAL SYSTEMS, CLASSICAL MODELS

account (1.1.74'), admitting that the function under the integral sign is continuous and

choosing the domain

V arbitrarily, then the principle of mass conservation leads to

Jμμ,

(1.1.76)

where

()tμμ and =

()tμμ . This is d’Alembert’s condition of mass continuity.

One observes from (1.1.76) that

μ is a relative scalar, i.e. a scalar density, the

denomination given to such a quantity being thus justified.

If at any moment we have a relation of the form

1J or

μμ, then the motion

is incompressible (or the body is incompressible).

One may also put the condition of mass conservation (invariance), equating to zero

the derivative of the mass (1.1.74') with respect to time; one obtains

()

(

)

dd d

dd dd

JV J V

tt tt

μμ==+

∫∫

We notice that we may write (see Chap. 2, Subsec. 1.2.3)

⎡

⎤⎡⎤

∂∂

∂

⎢

⎥⎢⎥

∂

∂∂

⎣

⎦⎣⎦

det det

tt t

00 0

ijk lmn

xx x

∂

⎛⎞

=∈∈

⎜⎟

∂

∂∂ ∂

⎝⎠

00 0 00 0 00 0

jjj

ikikik

ijk lmn

mn mn mn

lll

xvx

xxv

vxx

xx x xx x xx x

∂∂∂

⎛⎞

=∈∈ + +

⎜⎟

∂∂ ∂ ∂∂ ∂ ∂∂ ∂

⎝⎠

where we used the formula (2.1.36''), corresponding to the development of a

determinant; if we interchange indices

i and

and indices l and m with each other,

respectively, in the second sum, and indices

i and k , and indices l and m with each

other, respectively, in the third sum, and if we take into consideration the properties of

Ricci’s tensor, then we obtain

00 0 00 0

d1 1

d2 2

jpj

ik i k

ijk lmn ijk lmn

mn mn

xx x xx x

∂

∂∂

=∈∈ =∈∈

∂

∂∂ ∂∂∂

where we expressed the components of the velocity of a point of the mechanical system

as functions of the co-ordinates

x ,

1, 2, 3j . Taking now into account the relation

(2.1.37'), it follows that

∂

tx x

where we have introduced the velocity components of a point of the mechanical system

Newtonian model of mechanics

∂

===

∂

 ,

1, 2, 3j ;

(1.1.77)

we obtain thus

Euler’s formula (here and in what follows, see App., §2)

= v

div

(1.1.78)

which is verified in any point of a continuous mechanical system and by any particle in

motion; this relation may be written also in the form

= v

ln div

(1.1.78')

Returning to the derivative of the mass

M with respect to time, which we equate to

zero, we can write

(

)

div d 0

μ=+ =

∫

v ,

where the volume

V is arbitrary. If the function under the integral sign is continuous,

then we may write

the condition of mass continuity in Euler’s form

div 0

(1.1.79)

Observing that

∂∂

=+ ⋅=+⋅

∂∂

grad grad

tt tt

μμ μ

μμ

(

)

+⋅vvvdiv div gradμμ μ,

we obtain the condition (1.1.79) also in the form

()

∂

vdiv 0

(1.1.79')

If the density is constant at any time, we obtain

vdiv 0 ,

(1.1.78'')

hence, the field of velocities is

solenoidal (the velocities form a field of curls). The

relation (1.1.79) can be expressed also in the form

ln div 0

(1.1.79'')

MECHANICAL SYSTEMS, CLASSICAL MODELS

The relations (1.1.78') and (1.1.79'') lead to

()

ln 0

;

hence, the product

Jμ is constant at any moment, being equal to

μ (corresponding to

the initial state). We return thus to the condition of mass continuity given by

d’Alembert. The forms in which the principle of mass conservation may be expressed

are thus obtained.

The transformation relation (1.1.75) puts in evidence the position vector

()

000

123

,,xxx , corresponding to the initial position

, and the position vector

()

123

,,xxx , corresponding to the actual position (an arbitrary moment t ); this

relation may be written in the vector form

(

)

rrr

;t .

(1.1.75'')

If the continuous mechanical system

S is immersed into the domain D of the volume

V in the actual state, then we admit that one may pass continuously from

D to D , by

means of the geometric transformation (1.1.75); we admit also that the inverses of these

functions

()

123

xxxxx

1, 2, 3i

(1.1.75''')

are univocally determined (in particular,

(

)

0000

123

,,;

xxxxxt= ). The functions

(1.1.75''') are univocally determined, at least in a neighbourhood of the considered point,

if and only if the functions (1.1.75) are of class

()CD and the Jacobian (1.1.75') does

not vanish in this domain. This hypothesis is known as the

continuity axiom, which

expresses the

indestructibility of matter. A domain to which corresponds a finite

positive volume cannot be transformed in a domain of zero or infinite volume; this

implies also the

impenetrability of matter. The motion (1.1.75) or (1.1.75''') transforms

each domain in a domain, each surface in a surface and each curve in a curve. We admit

that the domain

D is limited by a sufficiently regular surface

S , which verifies, for

instance, conditions of the Lyapunov type. The equations (1.1.75) lead to the surface

S ,

which is the frontier of the domain

D and the image of

S by this transformation; this

surface also verifies conditions of Lyapunov’s type.

We admit that the variables

x ,

1, 2, 3i , corresponding to the domain

D (in the

initial state), are independent variables, and call them

Lagrange co-ordinates (or

material co-ordinates); this denomination was given because, in the phenomenon to

study, a point of the continuous mechanical system is followed in its motion. They are

referential co-ordinates; indeed, they give the position of the point with respect to the

initial state, considered as a frame of reference. In such a formulation, the co-ordinates

of the domain

(the material continuum in the actual state) are the unknown functions

of the problem, which must be determined. As well, we may consider variables

x ,

= 1, 2, 3i , as independent variables, calling them Euler co-ordinates (or spatial

Newtonian model of mechanics

co-ordinates); one has given this denomination because, at a point in space, there are

observed points of the continuous mechanical system which pass through this spatial

position in their motion. The unknown functions can be, for instance, the components of

the velocity at this point.

1.1.10 Classification of bodies

We have seen at Subsec. 1.1.8 that bodies can be modelled as mechanical systems

(discrete or continuous). In the case in which the mutual distances of all pairs of points

of a mechanical system remain invariant in time, we say that we have to do with a

non-

deformable mechanical system

(in particular, a rigid solid, which is a non-deformable

continuous medium); otherwise, we have to do with a

deformable mechanical system (in

particular, a

deformable continuous medium).

The deformable continuous media may be

deformable solids (which change little

their form under external loads, for instance under the action of forces) or

fluids (which

change very much their form, taking the form of the surrounding bodies, under the

action of external loads). The fluids may be

liquids (which change little their volume) or

gases (which change very much their volume, being expansive). The boundaries of

these classical types of continuous deformable media cannot be perfectly settled (as one

could expect from the definitions given above), because there exist media which have

simultaneously, for instance, properties of a solid body as well as properties of a liquid

one (in the same physical conditions).

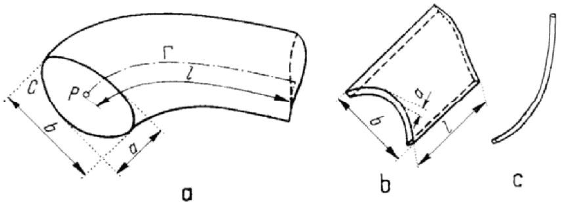
Figure 1.15. Curved bar (a). Thin walled bar (b). Thread (c).

In what concerns the deformable solids, one can put in evidence the properties

elasticity (if the causes which have led to the deformation of the solid cease their

action, then this one returns to its initial form; the deformation is reversible),

plasticity

(if, after moving off the causes which have led to the phenomenon of deformation, one

obtains a permanent deformation) and

viscosity (variation of the deformation as a

function of time); we mention thus elastic solids, elastoplastic solids, viscoelastic solids,

elastoviscoplastic solids a.s.o. The fluids can have also properties of elasticity and

viscosity, justifying thus the affirmation made above concerning bodies which can have

simultaneously properties corresponding to the two states of aggregation.

We mention also that a fourth state of aggregation of matter has been put in evidence:

the plasma. This is a state of the matter at high temperature; it is piecewise

electroconductive and in average neutral. Matter is thus a mixture of particles (some of

them have a positive or negative electric charge, and other ones are neutral), which are

MECHANICAL SYSTEMS, CLASSICAL MODELS

directed along the force lines of a magnetic field. The plasma is thus a deformable and

electroconductive continuous (or discrete) medium (for instance, a gas piecewise or

totally ionized).

If the body does not change its volume during the motion, then we say that it is

incompressible; this is an approximation of the physical reality. In general, the bodies

are compressible. We make now a classification (a modelling) of the deformable solids

according to their dimensions.

Thus, the bodies which have a dimension (the length) much more longer than the

other two dimensions (corresponding to the cross section) are called

bars. We will give

a constructive definition of this notion. Let be a curve

Γ (the axis of the bar) of finite

length

. In the plane normal to

at the point

∈

P Γ

, let us consider a closed curve

C , bounding a plane domain D (the cross section of the bar); we suppose that the

centre of gravity of the domain

D is at the point P . If the point P describes the curve

, then the curve

, which may be deformable, generates a surface, the boundary of a

three-dimensional domain, support of a body called

bar (Fig.1.15,a). Corresponding to

its axis, a bar may be

straight or curved; the last one can be a three-dimensional curved

bar

or a plane curved bar. The two (mean) dimensions a and

of the cross-section are

considered of the same order of magnitude, with the condition

,ab l . If all three

dimensions are of different order of magnitude

(

)

abl , we have to do with thin

walled bars

(Fig.1.15,b). Finally, if the two dimensions of the cross-section are

completely negligible with respect to the length of the bar, so that this one be perfectly

flexible and torsionable (without opposition to bending or torsion), then we obtain a

thread (Fig.1.15,c).

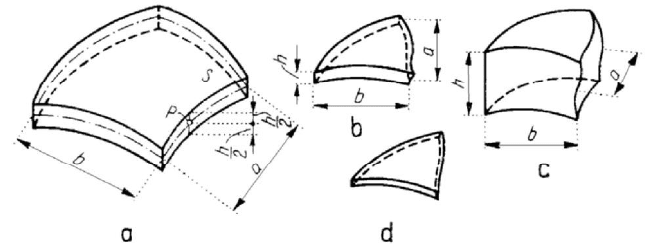
Figure 1.16. Plate (a). Thin plate (b). Plate of mean thickness (or thick plate) (c). Membrane (d).

The body, a dimension (the thickness) of which is much smaller than the other two

dimensions (corresponding to the middle surface) is called a

plate. Let be given an

arbitrary surface

S (the middle surface of the plate) of finite area. Along the normal to

S at a point ∈PS, let us consider a segment of length h (the thickness of the plate),

the middle of which is on

S , at the same point P . If the point P describes the surface

S , then the extremities of this segment, which may be of variable length, generate two

surfaces, boundary of a three-dimensional domain, support of a body called

plate

(Fig.1.16,a). Corresponding to the form of the middle surface, the plates may be

plane

(denominated simply

plates) or curved (denominated shells). The ratio between the

Newtonian model of mechanics

(mean) dimensions

a and b of the middle surface and the thickness h of the plate

leads to:

thin plates (for

,hab

) (Fig.1.16,b), plates of mean thickness and thick

Figure 1.17. Block.

plates

(for which < ,hab) (Fig.1.16,c). We observe that one cannot make a very good

delimitation between these categories of plates; they depend on the possibilities of

computation of the states of stress and strain, and can be different from case to case.

Finally, if the thickness

h is completely negligible with respect to the other two

dimensions, so that the plate is perfect flexible, then we obtain a

membrane (Fig.1.16,d).

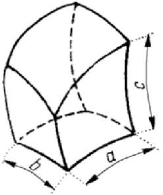
The bodies for which all three dimensions

a ,

and c are of the same order of

magnitude are called

blocks (Fig.1.17).

Generally, the real bodies have as supports finite three-dimensional domains. But we

will consider also infinite domains, the study of which present a special interest; indeed,

such domains are ideal models for real cases which one may often encounter in practice

or may be used as intermediary steps in solving problems for other domains.

1.1.11 Force. Field. Classification and representation of forces. Internal forces

Another element appearing in the mathematical modelling of a mechanical

phenomenon is the cause which yields the mechanical motion, being mentioned in

previous subsections. From a mechanical point of view, bodies are acting one on the

other and often it is difficult to put in evidence the physical nature of such an action; in

general, it received the name of

force. This denomination, resulting from the action of

the human being on the external world, gets a special meaning in mechanics; it is a

measure for the transmission of motion. The origin of forces is not always of

mechanical nature, but the goal of mechanics is not to determine their nature; mechanics

admits that forces are given.

Taking into account the property of inertia of a material point, its natural state is the

state of rest or uniform rectilinear motion; the force is the cause which is changing this

state. It appears thus the connection between the force and the variation of the velocity

(or of the momentum). We have seen in Subsec. 1.1.6 that the momentum is a measure

of the mechanical motion, remaining constant if the mechanical system is not acted

upon by another mechanical system (e.g., the case represented by relation (1.1.26)); if

the mechanical system is subjected to such an action, then appears a variation of the

momentum, hence a variation of the velocity (an acceleration). Thus, the force

applied to a point of the mechanical system is a vector quantity (as well as the variation

of the momentum to which it corresponds). From the experiments, it follows that – in

the most general case – the force may be modelled by a bound vector of the form

MECHANICAL SYSTEMS, CLASSICAL MODELS

(

)

FFrv;;t ,

(1.1.80)

where

r is the position vector of the point of application (belonging to the mechanical

system), while

v is its velocity; in components, we have

()

123123

,,,,,,;

FFxxxvvvt,

1, 2, 3i .

(1.1.80')

The force corresponds to the interaction of bodies and is emphasized in various

manners; thus, we distinguish between

contact actions and actions at distance. The

action of a homogeneous sphere, which is in collision with another homogeneous sphere

(case considered in Subsec. 1.1.6), is a contact action. The force by which the Earth acts

upon material bodies, in such a way that they fall on it, represents an action at distance.

Such an action at distance is called a

field. In general, a field is a domain D of the

space, which constitutes a zone of influence of a mechanical system

S or of a certain

mechanical phenomenon; in the presence of

S , the domain D acquires a special state,

so that the evolution of any other mechanical system, which has properties permitting to

be influenced by

D and passing through D , is changed. For instance, by its property

of mass or of electrical charge, a body generates a gravitational or an electric field,

respectively; any other body, which passes through such a field, is influenced in its

motion. In a continuous model of mechanics, the action of such a field upon a

mechanical system is characterized by a force; it is supposed that this action is

instantaneously propagated (otherwise, one must introduce a factor of delay in the

mathematical modelling of the phenomenon). So, we do not introduce in computation

the real action, which took place with a time lag. In a non-classical model, the

hypothesis of propagation step by step is used; indeed, the experience shows that no

action is propagated instantaneously. In fact, the hypothesis of the instantaneous

propagation corresponds to the hypothesis of the universal (absolute) time.

Modelling the force by a bound vector (1.1.80) (it is characterized by direction,

intensity (modulus) and point of application, properties corresponding to an intrinsic

definition of such a mathematical entity), this one will enjoy all the properties of bound

vectors (for instance, the summation of vectors). So, the action of two forces applied at

a point of the mechanical system

S can be replaced by the action of only one force

applied at the same point, along the diagonal of the parallelogram formed by the

mentioned forces; the reciprocal of this affirmation is, obviously, true: the action of a

force at a point can be replaced by the action, at the very same point, of two forces

representing the sides of the parallelogram, the diagonal of which is the given force.

Attaching to each point (of position vector

r ) of a domain D a vector F , at any

moment, we obtain a

field of forces of the form (1.1.80). If

does not depend

explicitly on

()

∂∂==FF0/ t



, then the field of forces is called stationary. In fact,

for any field and any mechanical phenomenon, which have this property, the same

denomination is used.

Because the forces are modelled by bound vectors, we may consider also

systems of

forces

(discrete systems) in action upon a mechanical system (discrete or continuous),

which will be modelled by systems of bound vectors; obviously, all the results obtained

for these systems of vectors may be used for the corresponding systems of forces. Let

{}

≡=F , 1, 2,...,

inF be such a system of forces; it corresponds rigorously to a

Newtonian model of mechanics

discrete mechanical system. In the case of a continuous mechanical system, the support

of which is the domain

, the system F represents only an approximate modelling of

the physical reality. If the subdomain

⊂ DD , to which the load is transmitted, has

negligible dimensions with respect to the dimensions of the domain

D , its localization

can be punctual; in this case, the load is called

concentrated (or punctual). If at least one

of the dimensions of the subdomain

D cannot be neglected, the load is called

distributed (or continuous); one considers that it is transmitted continuously to the

respective subdomain. We may thus define

linear, superficial or volume loads, the

intensity of which is proportional to the elements of line, area or volume, respectively.

A distributed load constitutes a vector field, the geometric support of which is the

subdomain to which the load is transmitted.

The forces acting upon a mechanical system may be

external forces, which can

represent the action of other systems on the given one (eventually the action of systems

of non-mechanical nature, e.g., temperature fields, electromagnetic fields, fields of

radiation etc.), or

internal forces, which represent the action of certain points of the

given system upon other points of the same system (these forces can also be of non -

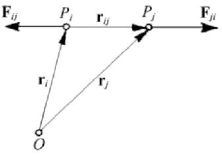
mechanical nature). Let be the points

P and

P of the given system; the force

F will

represent the action of the point

P upon the point

P , having the support

(

ij i j

PPλ

JJJG

, λ scalar). We introduce also the internal force

F , defined analogously;

these forces appear always as a pair and are linked axiomatically by the relation

(Fig.1.18)

Figure 1.18. Internal forces

ij ji

= −FF.

=FF 0

ij ji

(1.1.81)

1.1.12 Conservative forces

Upon a mechanical system (discrete or continuous) can act a field of forces, which

may be conservative or non-conservative.

The conservative forces (which derive from a

potential) are modelled by conservative vectors, expressed in the form

==∇=Fi

grad

UUU,

FU,

(1.1.82)

where

()

123

() , ,UU Uxxx is the force function (potential function or

potential). One can have

()

(

)

123

;,,;UU t Uxxxt in the representation (1.1.82);

the function is called

quasi-potential, and the forces are quasi-conservative in this case.