Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

582

trajectory not being affected by a decisive influence; thus, if the velocity of the

interplanetary vehicle is less than the second cosmic velocity of a celestial body in the

vicinity of which it passes at the distance

r , then the vehicle is captured by the

respective celestial body.

2.2.3 Study of conditions to become a satellite

One can obtain a graphical image of conditions to become a satellite by introducing

the non-dimensional variables

ξ =−=≥

gR v

⎛⎞

⎜⎟

⎝⎠

;

(9.2.41)

the conditions (9.2.35), to which we associate also the first condition (9.2.33'), take the

form

12 2

(1 ) (1 ) sin 1

ξξ

ξξα

−

≤≤<

++ −

⎡⎤

⎣⎦

(9.2.42)

with

sin

≥−

(9.2.42')

In a system of co-ordinate axes

Oξη we draw the arcs of rectangular hyperbola

γ and

γ of equations (Fig.9.14)

−

;

(9.2.43)

the domain

D , the points (, )ξη of which verify the conditions (9.2.42) to become a

satellite, is contained between these curves and the axes

Oη ( 0ξ ≥ ) and Oξ ( 0η > ).

To specify this domain we draw also the curves

()γγα

of equation

(1 ) (1 ) sin 1

ξξα

+−

⎡

⎤

⎣

⎦

(9.2.43')

Because

[]

2(1 )sin2

(1 ) (1 ) sin 1

ξξ α

ξξα

=−

++ −

it results that

d/d 0ηα< for

(0, /2)απ

∈

d/d 0ηα

for

/2απ= and

d/d 0ηα> for

(/2,)αππ∈ . Hence, if

α increases from

0α

(without that

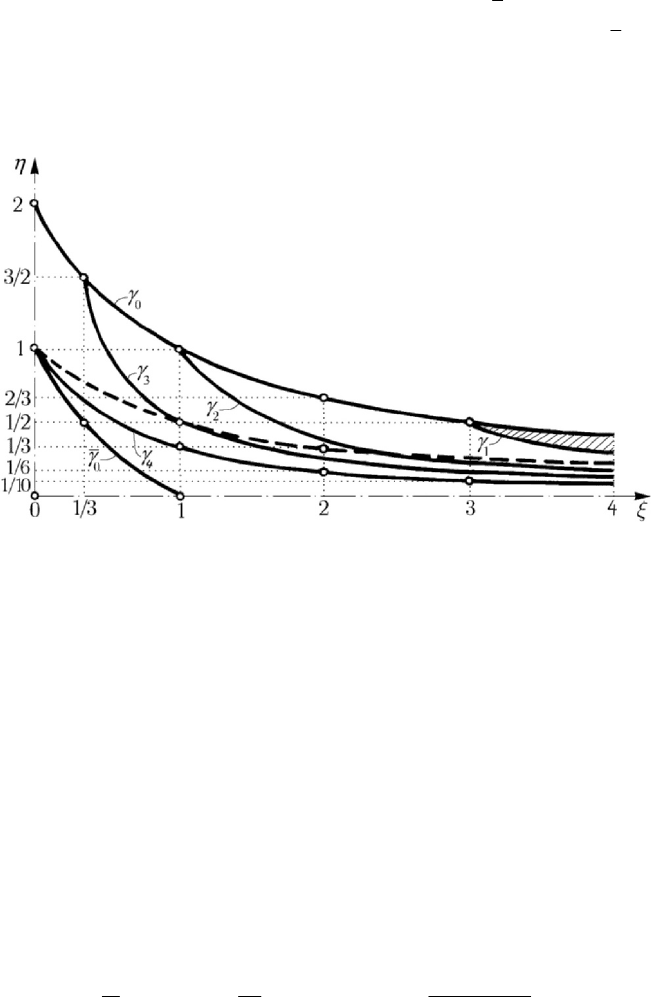
Newtonian theory of universal attraction

583

value), then the curve

()γα goes down till a position corresponding to

/2απ= ;

then

()γα goes up together with the increasing of

α . We notice that

() ( )γα γπ α=−. The curves

()γα are over the curve

, so as it was to be

expected (only the curve

(/2)γγπ

has a common point with the curve

). The

domain

()DDα

for which exists the possibility to become a satellite (a height H

being given, there corresponds a lot of possible initial velocities

v ) is contained

between the curves

γ and

()γα (without the frontier

γ ), which are piercing at the

Figure 9.14. Graphic representation of the conditions to become a satellite in the Oξη - plane.

points of co-ordinates

cotξα= ,

2sinηα= . In Fig.9.14 are drawn the curves

(/6)γγπ= ,

(/4)γγπ= ,

(/3)γγπ

and

(/2)γγπ

(the domain

(/6)D π for which one gets a satellite is hatched). The maximal such domain is

(/2)D π and is contained between the curves

γ and

γ , being bounded by the axis

0ξ =

. Indeed, only in this case we may have

; if

/2απ

≠

, then a possibility

to become a satellite takes place only for

cotξα> .

(9.2.44)

The condition (9.2.42') is included in the condition (9.2.44) because

(1 sin )/ sinαα−

cot α< .

The trajectory of the satellite is a circle if the eccentricity vanishes (

0e =

); taking

into account (9.2.7), (9.2.7') and observing that

MgR= , we must have

simultaneously

⎛⎞

−=

⎜⎟

⎝⎠

cot 0

22 2

00 0

sinrv

MECHANICAL SYSTEMS, CLASSICAL MODELS

584

It results that

/2απ= ,

//vgRRr= . With the notations introduced above, we

may write

;

(9.2.45)

this arc of rectangular hyperbola (contained in the maximal domain

(/2)D π ),

represented by a broken line in Fig.9.14, specifies the velocity

v by which a vehicle

must be launched in the space from a given height

H so that to become a satellite of

the Earth, having a circular trajectory.

An analogous study has been effected by L. Dragoş, using the non-dimensional

variables

/rR and

/vgR.

Figure 9.15. Graphic representation of the conditions to become a satellite

in the

OXY - plane.

A graphical interpretation of the conditions to become a satellite may be obtained in

the hodographic plane too; following a study made by C. Iacob (who used the

dimensional co-ordinates

cosv α and

sinv α ), we introduce the non-dimensional

co-ordinates

000

cos cos cos

ααηα== =,

000

sin sin sin

ααηα== =

(9.2.46)

of the extremity of the position vector

/vv. The conditions (9.2.35) to become a

satellite take the form

Newtonian theory of universal attraction

585

ξξ

−

≤+<

(2 )

ξξ

+−≥

(9.2.47)

to which we associate the condition (9.2.42'); we took into account the notation

(9.2.41). The first inequalities show that the point

(,)XYP must be in the interior of

the circular annulus, bounded by the circles

C and

C of radii

(1 )/(1 )ρξξ=− + and

2/(1 )ρξ=+, respectively, or on the internal frontier

of it (Fig.9.15). As well, this point must be interior to the hyperbola

H of equation

(regions of the plane which do not contain the origin

)

βα

−

(9.2.48)

and of semiaxes

2/(1 )αξξ=+ and 2/(1 )(2 )βξξ=++; the foci (0, )γ and

(0, )γ− are specified by 2(1 )/(2 )γξξ=+ +. The asymptotes of the hyperbola

make an angle

ϕ given by cot (2 )ϕξξ=+ with the

-axis.

If we draw a tangent from the launching point

to the Earth sphere, then we notice

that the angle

ϕ is just the angle made by this tangent with the straight line

′

(Fig.9.13). The condition (9.2.42') leads to

cot (2 )αξ ξ

≤

+ , so that

cot cotαϕ≤

;

hence,

αϕ≥

(the point (,)XYP must be in the interior of the asymptotes’ angle,

which contains the hyperbola

H, condition which is fulfilled together with the second

condition (9.2.47)). If

αϕ

(the point (,)XYP being in the interior of the

asymptotes’ angle, which does not contain the hyperbola

H ), then the trajectory of the

vehicle launched from the Earth surface pierces the Earth sphere immaterial of the

launching velocity. These conditions are easily justified in Fig.9.15.

We have

ρβρ<<. Hence, one can launch satellites of the Earth from a given

height

H , that is for a given ξ , if the initial velocity

v and the direction of the

launching

α are so that the point (,)XYP be in the interior of the domain D

bounded by arcs of hyperbola

H and arcs of circle

C (the hatched regions in Fig.

9.15). The points

+−

PPP and

−

P of intersection of the hyperbola H with the

circle

C have the co-ordinates

2/(1 )X ξξ

±+

2/(1 )Y ξ

±+

. The angle

formed by the OY -axis with the semi-lines O

P and O

−

P is given by

arctanαξ= ; it results that the launching angle

α depends on ξ , hence on the

launching height

H , and that we must have

[

]

/2 , /2απ απ α

∈

−+.

The point

(

)

0,1/ 1 ξ+ corresponds to a circular trajectory.

The discussion has been made for

0Y > ; for 0Y

one obtains analogous results

and a trajectory symmetric to the first one.

In conclusion, if the point

(,)XYP belongs to the interior of the circle

C , then

the trajectory is an ellipse (if

∈

PD, then the trajectory does not intersect the Earth’s

MECHANICAL SYSTEMS, CLASSICAL MODELS

586

sphere), if the point

P is on the circle

C , then the trajectory is a parabola, while if the

point

P belongs to the exterior of the circle

C , then the trajectory is an arc of

hyperbola. A supplementary study is necessary to see if these arcs of parabola or of

hyperbola intersect the Earth’s sphere.

2.2.4 Study of the satellite orbit

As we have seen in Subsec. 2.2.2 too, in a more exact theory we must take into

account the resistance of the atmosphere. As well, we must notice that the Earth is

neither spherical, nor homogeneous, so that the potential created by it is only with a

certain approximation equal to the potential of a particle situated at the mass centre of

the Earth and at which would be concentrated its whole mass; we may use with a better

approximation the formula (9.1.18) for the potential

()Ur of the terrestrial spheroid.

The equation of motion reads (

m is the satellite mass)

grad

mfm Umψ=−av,

(9.2.49)

where we have introduced the resistance

()

mtψ=−Rv, () (())tvtψψ= . In

spherical co-ordinates we can write (see Chap. 5, Subsecs 1.1.3 and 1.2.4)

222

sin

rr r f r

θθϕ ψ

∂

−− = −

∂



  

()

222 2

sin 2

rr f r

θθϕψθ

∂

−=−

∂





()

22 22

sin sin

rfr

θϕ ψ θϕ

∂

=−

∂

.

(9.2.49')

The terrestrial spheroid has properties of axial symmetry, so that

/0U ϕ

∂

∂=; the

third equation (9.2.49') leads thus to the first integral

()d

22 22

000

sin sin e

ψτ τ

θϕ θ ϕ

−

∫



(9.2.49'')

with

()rrt= ,

()tθθ= ,

()tϕϕ

. In particular, if the satellite is launched in

a meridian plane (

0000

() sin 0vt r

θϕ

= ), then sin 0vr

θϕ

= , hence

constϕ = ; thus, the satellite continues its motion in the meridian plane. In this case,

the equations of motion are

rr f r

θψ

∂

−= −

∂



 

()

rf r

θψθ

∂

=−

∂



(9.2.50)

If, in a first approximation, we take

/0U θ

∂

∂= , then we get a second first integral

(

()tθθ=



)

Newtonian theory of universal attraction

587

()d

ψτ τ

θθ

−

∫



(9.2.50')

which shows that the areal velocity

/2rΩθ=



has an exponential variation.

The spherical co-ordinates

()tθθ

and ()tϕϕ

of the satellite S being

determined, the problem to specify the orbit co-ordinates on the celestial sphere of

radius equal to unity is put. We choose a geocentric frame of reference (which we

assume to be inertial) with the origin at the Earth centre

P ; the principal plane is the

equatorial one and the

Px -axis is contained in this plane, being directed towards the

first point of Aries

γ (the vernal equinoctial point) (at the intersection of the equatorial

plane with the ecliptic plane, which contains the trajectory described by the Earth); the

Oz -axis is normal to this plane (it is the rotation axis of the Earth). The line of nodes

PN is specified by the angle Ω in the plane Pxy ; the plane of satellite’s orbit, which

passes through

PN , is inclined on the principal plane by the angle i . The position S

of the satellite is – in this case – given by

arcuNS

(Fig.9.16). Applying the

formulae of spherical trigonometry to the spherical triangle

NS S

′

, rectangular in S

′

we get the relations

Figure 9.16. Trajectory of a satellite.

cot tan sin( )i θϕΩ=−, cos sin cos( )u θϕΩ

− ,

(9.2.51)

which give the angles

i and u . We mention also the relation

sin sin cosiu θ

. (9.2.51')

2.3 Applications to the theory of motion at the atomic level

The motion of a particle electrically charged, e.g. of an electron in the vicinity of an

atomic nucleus, must be studied in the frame of the quantic model of mechanics;

however, one can obtain many interesting and useful results in the frame of the

Newtonian model too. After presenting the classical model of the atom, based on

MECHANICAL SYSTEMS, CLASSICAL MODELS

588

Hertz’s oscillator, we pass to the study of Bohr’s atom; by this occasion, we put in

evidence Ritz’s law too, which characterizes the lines spectrum of hydrogen.

2.3.1 Hertz’s oscillator. Classical model of the atom

If an electric charge

ee ε=  , where

e is the rationalized electric charge,

is the permittivity of the vacuum, while

 is a coefficient of rationalization ( 1= in

case of a non-rationalized system and

4π

 in case of a rationalized one, e.g., the

SI-system), passes from a condenser coat to another one (a rhythmical variation of the

armatures’ polarity by an alternative variation of the tension applied upon them), then

one obtains an experimental device which emits electromagnetic waves, equivalent to a

linear oscillator dipole of moment

000

/pp exε

= , where x is the elongation,

called Hertz’s oscillator. This device emits (i.e. it loses) energy in the form of

spontaneously radiated energy, expressed by the power

222

Pp ex

  ,

(9.2.52)

where

c is the velocity of light propagation in vacuum; the upper line indicates the

mean value. Starting from the equation of motion (8.2.23), we may write

242

xxω= ;

taking into account the form (8.2.24) of the solution and observing that

cos ( )d

ωϕ

−

∫

we obtain

2442

8xaπν= , where a is the amplitude, while ν is the frequency given

by (8.2.6'). It results

224

(9.2.52')

Thus, by radiation, a quantity of mechanical energy

d/dEt P

− is lost from the

mechanical energy

E given by (8.2.23''). We can write d/dEt Eγ

− , wherefrom

−

= ,

γ =

(9.2.53)

γ being the radiation constant; as it was shown by Max Planck, one obtains thus a

damping effect.

The classical model of the atom is an oscillator of Hertz, that is an electron which

oscillates around a position of equilibrium, where there is an atomic nucleus. But this

mechanical system loses permanently energy, as we have seen above; because of this

damped motion, after a sufficiently long (but finite) time, the electron falls towards the

nucleus. Such a model of atom is labile and does not correspond to the reality; but it can

be considered as satisfactory for a great lot of physical phenomena.

Newtonian theory of universal attraction

589

We notice that

EKa= , constK

; taking into account (9.2.53), it results also

for the amplitude a variation of the form

γ−

= ,

(9.2.54)

which characterizes a damped motion. Hence, the equation of motion of the electron

quasi-elastically linked in the atom should be of a corresponding form.

F is the force which arises under the influence of the atomic radiation, acting

upon the oscillator itself and damping its motion, then we are led to the equation of

motion

mx m x Fω+= ; multiplying by x , we obtain d/dEtFx= 

(

)

232

2/3ecx=−  (where we considered the non-averaged power), with

(

)

222

/2Emvmxω=+

. Taking into account (9.2.52) and observing that

d( )/dxxxt=   xx−  , we may write

Fx xx xx

=−

    ;

assuming that the period

T is sufficiently small, the second term may be neglected

with respect to the first one and we can take

 .

(9.2.55)

We obtain thus the equation of motion of the electron quasi-elastically linked to the

atom in the form

mx m x x

−=  .

(9.2.56)

Introducing the radiation constant

γ =

(9.2.53')

the equation (9.2.56) becomes

0xxx

ωω

γγ

−

−=  .

(9.2.56')

Choosing a solution of the form

()

xt e

= , we find the condition

3224

0γχ ω χ ω−−=

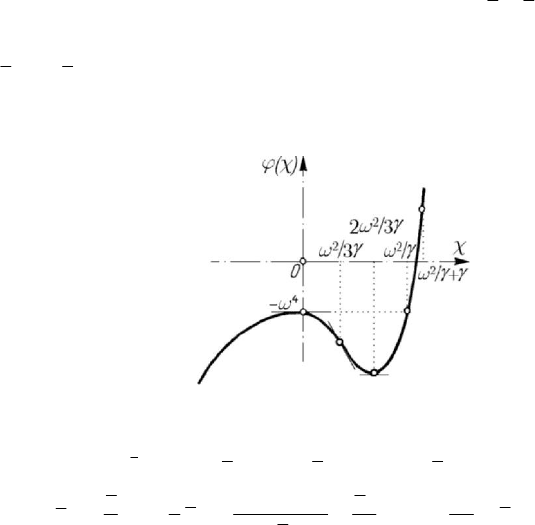
. Let us introduce the function

3224

()ϕχ γχ ωχ ω=− −

; we

notice that

()ϕ −∞ = −∞ ,

(0)ϕω

− , ()ϕ

∞

=∞. As well, d/dϕχ

3γχ=

2ωχ− ,

22 2

d/d 6 2ϕχ γχ ω=−. We obtain the graphic representation in Fig.9.17.

MECHANICAL SYSTEMS, CLASSICAL MODELS

590

We have thus only one real root of the form

/ωγγ

, (0, )γγ

∈

, because

(

)

/ϕω γ ω=− ,

(

)

(

)

2222

/2ϕω γ γ γ ω γ+= + ; the other two roots are

/2 iγω−± (the sum of the roots is

/ωγ). Hence, the general integral of the

equation (9.2.56') is of the form (we use the other two Viète’s relations between the

roots and the coefficients)

Figure 9.17. Graphic of the function ()ϕχ.

() e ( cos sin ) e

xt A t B t C

γω

ωω

′

−

=++, (0, )γγ

∈

222

γγω

ωωγ

γγ ω

=+= −

ωγ

′

+ .

(9.2.57)

The phenomenon corresponds to damped oscillations, so that one can take

0C = .

2.3.2 Bohr’s atom. Ritz’s law

The classical model of the atom gives some useful information with a sufficient good

approximation for some physical phenomena, but it is invalidated by other physical

phenomena, e.g. the spectral emissions (in the form of lines spectra). In 1913, Niels

Bohr, starting from Rutherford’s conception, which considers a model similar to that of

the solar system, develops a new model of the atom. Assuming the existence of a

central nucleus, formed by positive charges, and of electrons with negative charges,

attracted correspondingly to Coulomb’s law (1.1.84''), one obtains a mechanical system

in motion after Kepler’s laws. As a consequence of the lose of energy, on a way

analogous to that presented in the previous subsection, we are led to the motion of the

axis of the elliptic trajectory, hence to the possibility of falling of the electron towards

the nucleus (the so-called atomic catastrophe). To avoid such a phenomenon in the

mathematical model, N. Bohr completed it with following principles: i) The electrons

describe elliptic trajectories around the nucleus, after Kepler’s laws, without lose of

energy by radiation; from the set of all possible trajectories, these ones are stationary,

characterized by quantic conditions. ii) In conformity to the quantification conditions,

the integral of the generalized momentum corresponding to each generalized co-

ordinate (to each degree of freedom) along the complete trajectory must be an

integer multiple of Planck’s universal constant

6.626196 10 erg sh

−

⋅⋅ for the

Newtonian theory of universal attraction

591

stationarity trajectories. iii) The emission of radiations takes place only if the electron

“jumps” from a stationary trajectory on another stationary trajectory, due to an external

excitation.

In case of a single electron which moves around a nucleus, Bohr’s model

corresponds to the atom of hydrogen. We consider thus the motion of a particle of mass

m , which has a negative electric charge and moves around a positive centre of

attraction being acted upon by a Coulombian force which derives from the potential

/kr, 0k > . In our case,

/ke e ε==  , where

1.6021917 10 Ce

−

=⋅ (in

coulombs) is the electric charge in the SI-system; the coefficient

ε in (1.1.84'') is, in

this case, equal to unity.

Taking into account (9.2.6) and (9.2.12'), we may write the equation of the elliptic

trajectory in the form

(

)

1cos

e ψ

−

(9.2.58)

ψθθ=−

being the real anomaly. Because the kinetic energy is given by

(

)

222

/2Tmr rθ=+



, we define the generalized momenta corresponding to polar co-

ordinates by

pmr

∂



pmrmrmC

θψ

∂

== = =

∂





(9.2.59)

where

C is the constant of areas. The stationarity trajectories are thus specified by the

quantification conditions

pr nh

′

∫

dpnh

ψ =

∫

, ,nn

′

∈

` ,

(9.2.59')

where

h is Planck’s constant; the integrals are calculated along the complete trajectory

(for the first integral,

r varies from

min

r to

max

r and again to

min

r ). Observing that

()

dsin

dd1 d

(1 cos )

mr r m ma e

ψψ ψψ

⎛⎞

==−

⎜⎟

⎝⎠





22 22

sin sin

(1 cos ) (1 cos )

mr mC

ψψ

ψψ ψ

ψψ



we may write

sin sin cos d

1cos 1cos

(1 cos )

pr mCe mCe

ππ

ψψψψ

ψψ

⎛⎞

==−

⎜⎟

⎝⎠

∫∫ ∫

tan

1d arctan 2

1cos

mC mC

ψπ

⎛⎞

=−= −

⎜⎟

−

⎝⎠

−

∫