Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

532

where we take into account that the point

O is a stable position of equilibrium, the

force which acts upon the particle being directed towards this point (hence, it is equal to

F− ); we notice that the tension

T is of the form

()kl l

−

, assuming that the

thread is tensioned beginning with a length

2l , for which the initial tension is zero, so

that

kl T> . Because

() 2

xxxαβ=+ , we have () 12 0

xxβ

′

> for 0x > ;

hence, the arc characteristic is strong.

In the considered case, the force

F is conservative (

2()Vx x xαβ=+), so that

we may use the results in Chap. 6, Subsec. 2.2.4 and Chap. 7, Subsec. 2.3.4; we obtain

thus the first integral

224

vxxhαβ++=,

ha aαβ=+,

(8.2.85')

where

a is the maximal elongation, for which 0v

. The period is given by

() ()

24 2 2

1sin

hxx a

αβ αβ θ

−+ + +

∫∫

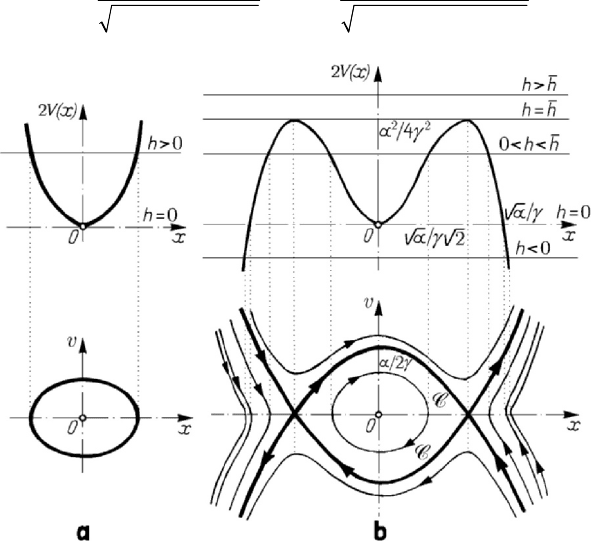
Figure 8.52. Motion of a particle situated at the middle of an elastic thread. Phase trajectories.

Diagrams 2()Vx vs

and v vs

: case

0β >

(a); case

0β

(b).

where we have made the substitution

sinxa θ

. If

0β >

(strong spring, case

considered above), then the frequency increases (the period decreases) together with the

amplitude; the motion is periodic, the phase trajectories being closed for any initial

conditions for which

0h ≥ (Fig.8.52,a).

Dynamics of the particle in a field of elastic forces

533

0βγ=− < (soft spring, weak characteristic), then the period increases together

with the amplitude; the potential energy has two maxima and a minimum (Fig.8.52,b).

For

/4hh αγ== one obtains the separation curve C, formed by arcs of parabola

(,) 2 2 0Pxv v xγγ α≡− +=,

(,) 2 2 0Pxv v xγγ α

≡

+−=.

For

hh> the phase trajectories cover the whole phase plane. For 0 hh<<

(

aαγ> ) one obtains closed phase trajectories, interior to the curve C, and open

curves, exterior to that one, while for

(

aαγ< ) there are only open phase

trajectories; the motion is periodic only for the closed curves, in initial conditions for

which

(,) 0Px v > ,

(,) 0Px v

. The point O is a singular point of centre type

(stable equilibrium), while the points

(

)

/2,0αγ± are singular points of saddle

type (labile equilibrium). Making

/2a αγ= , one obtains

sec dT

θθ

∫

on the separation curve; we notice that

(

)

sec d ln tan

πθ

θθ

∫

so that the particle

P reaches a labile position of equilibrium after an infinite time.

The cases considered above have led to equations of the form (8.2.83') and,

precisely, of the form

() 0xfx

= ,

(8.2.83'')

corresponding to the non-damped free vibrations of mechanical systems with non-linear

elastic characteristics. Let us assume that

()

x is an odd function ( () ()

xfx−=− ),

symmetric with respect to the origin, and let us suppose that at the initial moment

0t = the abscissa is

x and the velocity vanishes (

). In this case, multiplying

the equation (8.2.83'') by

x and integrating, one obtains

()d ()d

fx xξξ+=

∫∫



a relation which corresponds, in fact, to a conservation law of the mechanical energy.

Taking into account that

d/dxxt

 and integrating between the limits 0x = and

xx= , we obtain the period (assuming that

0x > , we take the sign minus before the

radical, because between the initial position and that of equilibrium the motion takes

place in the negative direction of the

Ox -axis)

MECHANICAL SYSTEMS, CLASSICAL MODELS

534

2()d

ξξ

∫

(8.2.86)

In general,

2()d

ξξ

∫

(8.2.86')

In particular, in the case of harmonic oscillations we have

()

xxω= and are led to

arccos

−

∫

As well, if

() sin

θω θ= (great oscillations of the mathematical pendulum), then the

formula (8.2.86) allows to find again the period (7.1.39'). In general, for the equation

(8.2.84) (and analogously for the equation (8.2.85)) the formula (8.2.86') leads to

elliptic integrals of the first kind, as it was to be expected.

The damped free vibrations of mechanical systems with non-linear elastic

characteristics lead to an equation of the form

() (,) 0xfx gxx

+=  ,

(8.2.87)

while the parametric vibrations of non-damped mechanical systems are modelled by an

equation of the form

() 0xtxω

= .

(8.2.87')

Sometimes, in case of small non-linearities, we may introduce a small parameter

ε ,

obtaining quasi-linear equations of the form

() 0xxfxωε

+= ,

(8.2.88)

[

]

() () 0xxfxgxωε++ + = 

(8.2.88')

(, ) 0xxfxxωε++ =  .

(8.2.88'')

We mention thus the Van der Pol equation (for self-excited vibrations)

(

)

10xx xxλ+− − =  , 0λ > ,

(8.2.89)

Rayleigh’s equation (for small non-linear dampings)

(

)

0xx mx nxε++ − =   , ,0mn> ,

(8.2.90)

Froude’s equation (for dampings in a turbulent motion of fluids)

Dynamics of the particle in a field of elastic forces

535

0xxpxqxγ

++=   ,

(8.2.90')

Duffing’s equation (for the response to a harmonic excitation of mechanical systems

with non-linear elastic characteristics)

cosxxxcxq tαβ ω++ +=  , 0c ≥ ,

(8.2.91)

Mathieu’s equation (for a harmonic variation in time of the rigidity)

(

)

cos 0xtxωα ω++ = ,

(8.2.92)

and Hill’s equation (for the periodic variation in time of the rigidity)

cos 0

xntxωαω

∞

⎛⎞

++ =

⎜⎟

⎝⎠

∑

 ;

(8.2.92')

the study of these equations has put in evidence the most important non-linear

phenomena and the corresponding basic methods of solution.

In general, for a free vibratory motion is searched a periodic solution (if there exists

such a solution for the given initial conditions) and a study of its stability is made. In

case of forced vibrations, the form of the response curves of the mechanical system (the

relation between the amplitude and the frequency of the motion and the corresponding

characteristics of the perturbing force) is searched too. The non-linear vibrations are

non-isochronous, because the period

T depends on the amplitude. As well, besides the

problem of static stability, the problem of dynamic stability must be also considered.

We have seen that the response of a damped linear system on which acts a sinusoidal

perturbing force of pulsation

ω is a harmonic vibration, having the same pulsation; in

case of a non-linear system appear pulsations

nω , n

∈

` , too, called also

superharmonics (multiples of the excitation pulsation) or even pulsations

/nω ,

n ∈ ` , called subharmonics (submultiples of the excitation pulsation). In case of the

action of two independent perturbing forces upon a non-linear system, one can no more

use the principle of superposition of effects; by the superposition of two distinct

excitations, appears an interaction between the oscillations which arise, leading to the

phenomenon of asynchronous suppression (if each of the independent vibrations is

stable, then one of the motions destroys the stability conditions of the other one), to the

phenomenon of asynchronous excitation (one of the independent vibrations is labile,

the other one being stable and creating the conditions that the first one become stable

too) or to the phenomenon of carrying the pulsations (if the independent vibrations

have close pulsations which, in a certain zone of values, synchronize).

2.2.14 Computation methods

The problems which arise in the study of non-linear oscillations are difficult, so that

their solution needs specific methods of computation, especially approximate ones. We

have thus presented in Chap. 7, Subsec. 2.3.4 topological methods of computation in

MECHANICAL SYSTEMS, CLASSICAL MODELS

536

the phase space, which have been used in the previous subsection. In what follows we

pass in review some approximate methods of computation.

Let be the quasi-linear equation (which intervenes in case of the mathematical

pendulum)

0xxxωε

+= ,

(8.2.93)

a particular case of the equation (8.2.88). In S.P. Timoshenko’s method we assume that,

in a first approximation,

() cosxt a tω

(8.2.93')

represents a harmonic motion of pulsation

ω , which differs not much from

ω and for

which the initial conditions

(0)xa

, (0) 0x



(8.2.93'')

are verified. We notice that

22 2

ωω ω

+Δ ,

222

ωωωΔ= −, and put the condition

that the solution (8.2.93') verifies the equation (8.2.93), obtaining thus

(

)

22 33 23 3

cos cos cos cos 3

xxa ta t a a ta t

ωωωεωωεωεω+=−Δ − =−Δ+ − .

The first term of the second member represents a perturbing element with the same

pulsation as the proper one of the terms in the first member; but this term must be

equated to zero (

3/40aaωεΔ+ =) to can eliminate the phenomenon of resonance.

With the same initial conditions, we obtain, in a second approximation, the solution (to

the general solution of the homogeneous equation we add a particular solution of the

complete equation)

() cos cos3

32 32

xt a t t

εε

ωω

⎛⎞

=− +

⎜⎟

⎝⎠

(8.2.93''')

with

22 2

ωω ε=+ .

(8.2.94)

Analogously, we may use the Ostrogradskiĭ-Lyapunov method, based on successive

approximations too. We choose thus the solution in the form of a polynomial in

ε (we

consider only the first three approximations)

xx x xεε=+ + ,

(8.2.95)

where

()xxt

()xxt= ,

()xxt

are functions of class

C ; as well, we

take (we retain only three terms)

Dynamics of the particle in a field of elastic forces

537

22 2

CCωω ε ε=+ + ,

(8.2.95')

where

,,CCω are non-determinate constants. Replacing in (8.2.93) and equating to

zero the coefficients of the powers of

ε , we obtain

0xxω+=

111

0xxCxxω

++=

22112 1

30xxCxCxxxω++++ = .

The first of these equations leads (for

x ) to the first approximation (8.2.93') with the

same initial conditions (8.2.93''); replacing

x in the second equation and determining

C so that the phenomenon of resonance be eliminate, we find again for

xx xε=+

the same approximation (8.2.93'''). Analogously, we may determine

x , thus the third

approximation a.s.o. We notice that the two methods of successive approximations are

– as a matter of fact – equivalent, differing only by the modality of approaching the

computation. The non-linearity of the considered phenomenon has introduced

superharmonics in the equation (8.2.93) (harmonics of third order in the approximation

of second order).

In case of the equation (8.2.83'') we introduce the square deviation

[

]

()

xxωΔ= − between the non-linear term and the linear approximation; using

the solution in the linear case

cosxa tω

, we obtain the mean square deviation on the

duration of a period

[][]

22 2

( cos ) cos d ( cos ) cos d

fa t a t t fa a

ωω ω θω θθ

=−= −

∫∫

A ,

where a change of variable

tωθ

has been made. Imposing the condition that

minimal (the least squares method), hence the condition

/0ω

∂

∂=A , we are led to

(cos)cosdfa

ωθθθ

∫

(8.2.96)

wherefrom we deduce

2/T πω= . In particular, in case of the equation (8.2.93), the

formula (8.2.96) leads to the pulsation (8.2.94), so that

223

ππ

ωε

⎛⎞

=≅−

⎜⎟

⎝⎠

(8.2.94')

in case of a small parameter

ε . We notice that for 0ε > (non-linear vibrations with

strong characteristic) the period decreases with the amplitude, while for

0ε < (non-

linear vibrations with weak characteristic) the period increases with the amplitude; if

0ε = , then the vibrations are isochronous. We may thus easily determine,

experimentally, the nature of these vibrations.

MECHANICAL SYSTEMS, CLASSICAL MODELS

538

In the harmonic balance method, the condition that the term in

cos tω of the

development into series of the function

(cos )

atω be identical to the corresponding

term

cosatωω in the associated linear differential equation is put; thus, the formula

(8.2.96) is found again.

Other approximate methods of computation are based on the so-called variation of

constants, differing after the constants which are varied. We mention, e.g., Van der

Pol’s averaging method. In the Krylov-Bogolyubov method, the basis of which is the

first approximation theory, the constants which vary are the amplitude and the phase of

the motion of the non-linear system. However, the method has numerous variants, e.g.

the Bogolyubov-Mitropol’skiĭ variant.

We mention the equivalent linearization method (Krylov-Bogolyubov) too, as well as

Galerkin’s method.

Thus, in case of the quasi-linear equation (8.2.88'') we start from the harmonic

solution

sin( )xa tωϕ=−,

cos( )xa tωωϕ

− ,

and take the amplitude

()aat

and the phase shift ()tϕϕ

as new unknowns,

functions of time, which must be determined. Differentiating with respect to time, we

obtain

0000

sin( ) cos( ) cos( )xa t a t a tωϕϕωϕ ω ωϕ=−− −+ −  ;

taking into account the expression of the velocity which corresponds to the linear case,

there results the condition

sin( ) cos( ) 0at a tωϕϕωϕ

−

−−= .

Starting from the same expression of the velocity, we may write

00 0 0 00

cos( ) sin( ) sin( )xa t a t a tωωϕωϕωϕωωϕ=−+ −−−   ,

and taking into account the equation (8.2.88''), we get

00 0 0

cos( ) sin( )at a tωωϕωϕωϕ−+ −

(

)

000

sin( ), cos( )

ata tεωϕωωϕ

−− −;

using also the condition previously obtained, we get the differential equations of first

order (instead the differential equation of second order)

()

000 0

sin( ), cos( ) cos( )afata t t

ωϕω ωϕ ωϕ

=− − − −



()

000 0

sin( ), cos( ) sin( )fa t a t t

ϕ ωϕω ωϕ ωϕ

=− − − −



(8.2.97)

We notice that the function

has the period

2/T πω

and that a and ϕ vary

slowly in time; these derivatives may be taken equal to their mean values

mean

a and

Dynamics of the particle in a field of elastic forces

539

mean

ϕ on a period (considered to be approximately equal to T ). In a period, the angle

tψω ϕ=− varies by 2π , so that

mean

d(sin,cos)cosd

aa faa

ππ

ψψωψψψ

ππω

==−

∫∫

 ,

mean

d ( sin , cos )sin d

fa a

ππ

ϕϕψ ψωψψψ

ππω

==−

∫∫

 ,

(8.2.97')

corresponding to the first terms in the respective development into Fourier series. For a

better approximation, one may take terms of higher rank in these expansions.

()

fx= , () ()

xfx−=− , then we may write

(sin )cos d ()d 0

afa fxx

ππ

εε

ψψψ

πω π ω

=− =− =

∫∫

 ,

constaa

= .

(8.2.97'')

We obtain thus the approximate solution

[

]

() sin ( )xt a atωψ

− ,

(8.2.97''')

the pulsation depending on the amplitude, as an effect of the non-linearity. Squaring the

second relation (8.2.97') and neglecting

ε , we find the remarkable relation

( ) ( sin )sin dafa

ωω ψψψ

∫

(8.2.97

)

For instance, in case of the equation (8.2.84), we obtain

234

sin d 1

gg g

ll l

ωαψψ

πα

⎛⎞

=− = −

⎜⎟

⎝⎠

∫

where

max

αθ

is the amplitude of the mathematical pendulum; it results the period

21 1

2221

lll

ggg

πα

πππ

⎛⎞

== ≅ ≅ +

⎜⎟

⎝⎠

−

finding again the approximate formula (7.1.43''') (if we limit ourselves to the first two

terms in the considered developments).

Let be also the Van der Pol equation (8.2.89) with the initial conditions

(0)xa= ,

(0) 0x = . Observing that

1ω

, ελ

− ,

(

)

(,) 1

xx x x=−

(the unit having the

necessary dimension), we start from the harmonic solution

sin( )xa tϕ

− ; the initial

conditions lead to

(0) (0)sin (0)xa aϕ=− = , (0) (0)cos (0) 0xa ϕ

= , so that

(0)aa=− , (0) /2ϕπ= . The formulae (8.2.97') give the mean values

MECHANICAL SYSTEMS, CLASSICAL MODELS

540

() ()

22 2

mean

1 sin ( cos )cos d 4

aaa aa

ψψψψλ

=− =−

∫

 ,

()

mean

1 sin ( cos )sin d 0

ϕψψψψ

=− =

∫

 ,

the system of differential equations of first order (8.2.97) becoming thus

()

aaaλ=−

 , 0ϕ

 .

Separating the variables in the first equation, integrating by decomposition in simple

fractions and taking into account the initial conditions for the new variables, we may

write

[]

() cos

(/2) 1(/2)e

xt t

λ−

+−

;

(8.2.98)

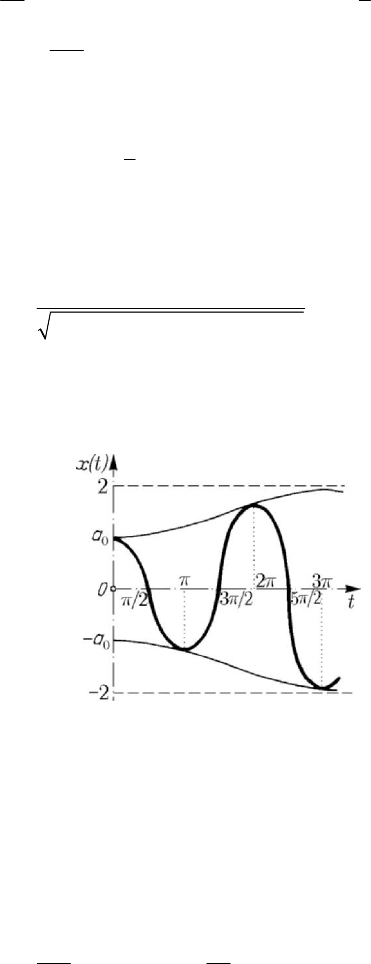
this result corresponds to an aperiodic oscillatory motion, hence to a vibration

modulated in amplitude, which tends asymptotically to 2 (in Fig.8.53 we assume that

2a < ).

Figure 8.53. Van der Pol equation. Diagram ()xt vs t .

The perturbations method, initiated by Poincaré, allows also an approximate study of

the differential equations with a small parameter. Let thus be an autonomous

mechanical system, the motion of which is modelled by a non-linear differential

equation of the form (8.2.88'') for which

(0,0) 0

, with the initial conditions

(8.2.93''). By the change of variable

tωτ

, where ω is a unknown pulsation, one

obtains an equation of the form

(

)

22 2

,, 0

xxωωεϕω

++ =

(8.2.99)

where

ϕ is a given non-linear function; the initial conditions become 0x = ,

d/d 0x τ = for 0τ = . In the perturbations method one considers both for the

Dynamics of the particle in a field of elastic forces

541

solution

()x τ and for the square of the unknown pulsation ω , developments into

power series after the small parameter

ε , i.e.

() () () () ...xx x xττετετ=+ + +,

(8.2.100)

22 222

...ωωεωεω=+ + +.

(8.2.100')

The initial conditions are verified if

... 0xx

==,

d/dx τ

d/dx τ=

d/d ... 0x τ===. Replacing in the equation (8.2.99), developing the function ϕ

(which we assume to be analytical) into a Taylor series, arranging the terms after the

powers of the small parameter

ε , and equating to zero the coefficients of those powers

(assuming successively, that one may neglect the higher powers of

ε with respect to

the lower ones), we get the equations

000

xωω

= ,

(

)

100

222 2

00 00

ωωωϕ ω

ττ

+=− −

210

2222

21 2

222

ddd

ωωωω

τττ

+=− −

(

)

(

)

(

)

ϕϕϕ

∂∂∂

−− −

∂∂

∂



. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

(8.2.100'')

In the first approximation, the small parameter ε is neglected; the first equation

(8.2.100'') leads to the solution

cos cos cosxa a ta tτω ω== = , (8.2.101)

which satisfies the initial conditions. In the second approximation,

, ,...εε are

neglected with respect to

ε , hence one takes

() () ()xx xττετ

+ ,

ωεω=+ . Replacing the solution (8.2.101) in the second equation (8.2.100''), it

results

()

cos cos , sin ,

xa a a

ωωτϕττω

⎛⎞

+= − −

⎜⎟

⎝⎠

with the initial conditions

d/d 0x τ

for 0τ

. In the second member of

the differential equation appear terms in

cos τ and sin τ (secular terms), which lead to

non-periodic particular solutions of the form

cosττ and sinττ. Because we search

periodic solutions, we equate to zero the coefficients of those terms, obtaining

supplementary conditions; we get thus

ω and may then integrate the differential

equation. The procedure can be applied further, obtaining thus approximations of

higher order (a solution

()x τ in the form of an expansion into a Fourier series).