Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

502

2/T πω= , multiple of the periods of all the other oscillations, hence the period of the

motion

()xt ), being called fundamental (or harmonic) oscillation. The oscillation

expressed by the term

cos( )

antωϕ

−

has the frequency

min

nνν

and is called

harmonic of nth order. The set of amplitudes and the set of phases of the harmonic

oscillations which compose a periodic motion form the amplitudes spectrum and the

phases spectrum, respectively.

2.2.5 Composition of orthogonal harmonic vibrations. Small oscillations around a

stable position of equilibrium

Let be the harmonic vibrations

11 1 1

cos( )xa tωϕ=−,

22 2 2

cos( )xa tωϕ

−

along two orthogonal directions (corresponding to the

Ox -axis and to the

Ox -axis,

respectively); by their composition, one obtains a motion the trajectory of which is

contained in the rectangle

111

axa−≤ ≤,

222

axa

−

≤≤.

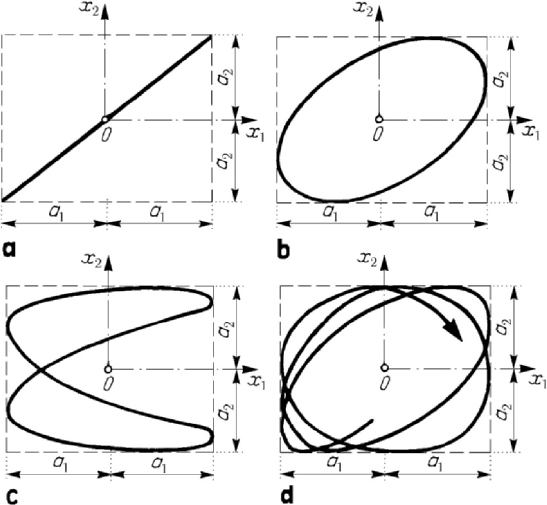
Figure 8.25. Composition of orthogonal harmonic vibrations:

ωω

ϕϕ= (a);

ωω= ,

ϕϕ≠ (b); Lissajous’ curves (c);

/ nωω

≠

, n

∈

 (d).

ωω= and

ϕϕ= , then, eliminating the time t , it results

2211

/xaxa= ,

hence the trajectory of the linear oscillator thus obtained is the diagonal of the

Dynamics of the particle in a field of elastic forces

503

mentioned rectangle (Fig.8.25,a). If

ωω

and

ϕϕ

≠

, then it results an elliptic

oscillator (Fig.8.25,b) of equation

22 22 22 2

21 12 1 2 12 12 12 1 2

2cos( ) sin( )ax aa xx ax aaϕϕ ϕϕ−−+=−

obtained by elimination of the time

ωω

≠

and

/ nωω

, n

∈

 (the pulsations

ω and

ω are

commensurable), then it exists a period

, the smallest common multiple of the

periods of the two component motions, so that the motion is periodic, while the

trajectory of the particle

is a closed curve, called Lissajous curve; the trajectory

corresponding to the case

2ωω

/4ϕπ

0ϕ

is given in Fig.8.25,c. If the

pulsations are not commensurable, then the motion can no more be periodic and the

trajectory is an open curve which covers the whole rectangle mentioned above

(Fig.8.25,d).

Analogously, one may compose three orthogonal harmonic vibrations

cos( )

ii i i

xa tωϕ=−, 1, 2, 3i

(8.2.32)

corresponding to the axes

Ox ,

Ox and

Ox , respectively; one obtains thus a

trajectory contained in the parallelepipedon

iii

axa

−

≤≤, 1, 2, 3i

. However, one

may thus study the small oscillations of a particle around the pole

O , considered as a

stable position of equilibrium. We assume that the force which acts upon the particle is

conservative (

gradU=F ), the potential U being developable into series

(

...UU U U=+++

, 0,1,2,...,i

homogeneous polynomial of ith degree in

the co-ordinates

123

,,xxx). Because the components of the force

are obtained as

derivatives of the potential

, we may take

; as well, we must have

0U =

because the origin is a position of equilibrium. Assuming that we have to do with small

motions, we take

UU=

, neglecting the polynomials of higher order; we notice also

that one must have

0U <

, the pole

being a stable position of equilibrium (the

trajectory must be entirely at a finite distance). One may take

()

22 22 22

123 112233

(, , )

Ux x x x x x

ωωω=− + +

(8.2.32')

in this case; we are thus led to the equations of motion

111

0xxω+= ,

222

0xxω

= ,

333

0xxω

= ,

(8.2.32'')

the solutions of which are the harmonic vibrations (8.2.32). The trajectory of the

particle

P is a closed curve (a Lissajous curve), the motion being periodic if and only

if the pulsations (hence the periods and the frequencies too) are commensurable (are

proportional to integer numbers

11 22 33

///nnnωωω

= ,

123

,,nnn∈  ).

Otherwise, the trajectory is an open curve which covers entirely the above mentioned

parallelepipedon; the particle does not pass twice through the same position, but may

pass as close as possible to it in a sufficiently long time.

MECHANICAL SYSTEMS, CLASSICAL MODELS

504

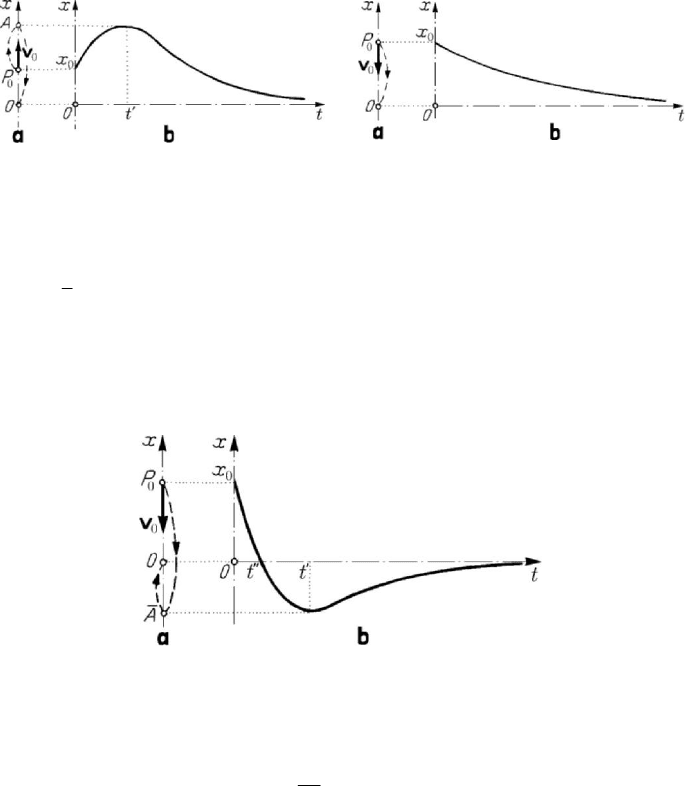
2.2.6 Damped linear oscillator

If, besides a linear elastic spring (Fig.8.8), we introduce, in parallel, a viscous

damper with a damping coefficient

′

> , then we obtain the physical model of a

damped linear oscillator (Fig.8.26). Using the notations in Subsec. 2.1.3, it results the

equation of motion (along the

Ox -axis)

Figure 8.26. Model of a viscous Figure 8.27. Damped linear oscillator: trajectory (a);

damped linear oscillator. diagram

()xt

vs t (b).

20xxxλω

+=  ;

(8.2.33)

with the initial conditions (8.2.23'), we obtain the solution

000

( ) e cos ( )sin e cos( )

xt x t v x t a t

λλ

ωλω ωϕ

−−

⎡⎤

′′′

=++=−

⎢⎥

′

⎣⎦

(8.2.33')

corresponding to a subcritical damping (

1χ

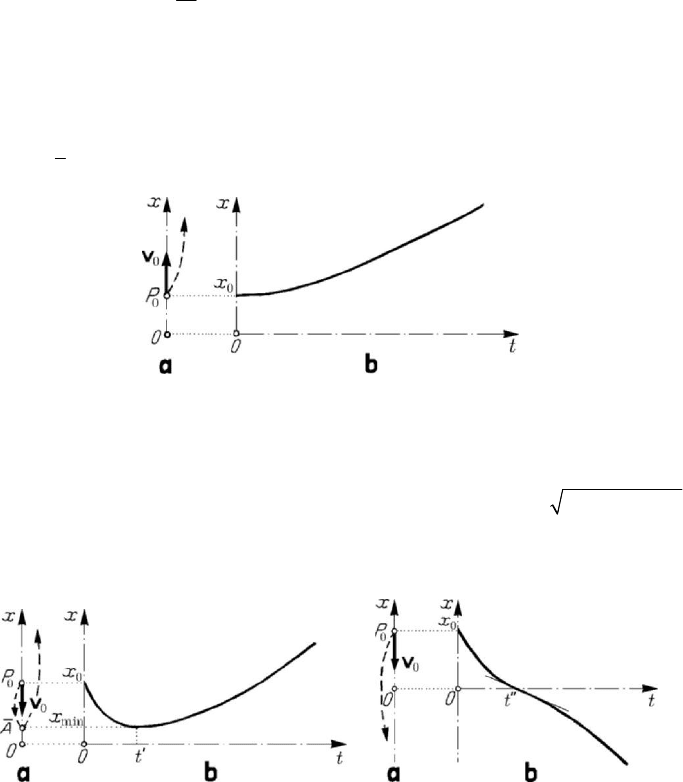
). The motion is a pseudoperiodic

damped motion, of pseudoperiod

2/T πω

′

, the trajectory of which starts from the

point

P , being contained in the segment of a line

and tending to the asymptotic

point

O after an infinity of oscillations around this pole (Fig.8.27,a). This motion

constitutes a vibration modulated in amplitude, being strongly damped; the diagram of

the motion has the aspect of a cosinusoid contained between the curves

λ−

=±

and tangent to these ones at the points

/t ϕω

′

, /tTϕω

′

+ ,… and /t ϕω

′

/2T+ , /t ϕω

′

3/2T+ ,…, respectively (Fig.8.27,b).

In case of a critical damping (

1χ

), we obtain an aperiodic damped motion given

[

]

00 0

() e ( )

xt x v x t

−

=++.

(8.2.33'')

0v >

, then the particle starts from the point

, reaches A at the moment

000

/( )tv v xλλ

′

=+, and then changes of direction tending asymptotically to the

Dynamics of the particle in a field of elastic forces

505

centre

O (Fig.8.28,a); the diagram of motion has a point of maximum for tt

′

= ,

tending asymptotically to zero (Fig.8.28,b). If

0xvλ

−

≤≤, then the particle starts

from

P , tending asymptotically to zero (Fig.8.29,a). The corresponding diagram has

neither zeros, nor points of extremum (Fig.8.29,b); in the case in which

/2 0xvλ−<< appears a point of inflection. If

vxλ

− , then the particle starts

Figure 8.28. Linear critical damping; case Figure 8.29. Linear critical damping; case

0v >

: trajectory (a); diagram

0xvλ

−

≤≤ (a); diagram

()xt vs

(b). ()xt vs

(b).

from

P , passes through the centre O at the moment

00 0

/( )txvxλ

′

−+ and

reaches

A at the moment t

′

and returns asymptotically towards the centre O

(Fig.8.30,a); the diagram of motion pierces the

Ot -axis at the point tt

′′

= , has a

minimum for

′

= , tending then asymptotically to zero with negative values

(Fig.8.30,b). If the point

P is at the left of the pole O , hence if

0x < , then one

obtains, by symmetry, analogous results.

Figure 8.30. Linear critical damping; case

vxλ

− (a); diagram ()xt vs t (b).

A supercritical damping (

1χ > ) leads to an aperiodic damped motion of the form

000

() e cosh ( )sinh

xt x t v x t

ωλω

−

⎡⎤

′

′′′

=++

⎢⎥

′′

⎣⎦

(8.2.33''')

In what concerns the trajectory and the diagram of motion, one obtains the same

qualitative results as above as

0v > ,

() 0xvλω

′

−

+≤≤ or

()vxλω

′′

<− +

(Figs.8.28-8.30); we observe that

MECHANICAL SYSTEMS, CLASSICAL MODELS

506

arg tanh

ωλ

′

′′

arg tanh

ωλ

′

−

′′

Multiplying the equation (8.2.33) by

mx , we obtain

()()

TV TU kv

′

+= −=−

(8.2.34)

so that the sum between the kinetic energy and the potential energy decreases (is

dissipated) in time. In case of a subcritical damping, we observe that (abstraction of an

additive constant)

[]

222

() () () e cos2( ) sin2( )

Et Tt Ut t t

ωλ ω ϕλω ωϕ

−

′′′

=−= + −+ −

so that

()e ()

Et T Et

−

+= ,

(8.2.34')

where

Tδλ=− is the logarithmic decrement of motion; hence, the mechanical energy

of the pseudoperiodic damped linear oscillator decreases in geometric progression.

The relative energy dissipated in an interval of time equal to a pseudoperiod is given by

() ( )

()

Et Et T

−+

==−

(8.2.34'')

being constant in time.

Figure 8.31. Model of a Coulombian damped linear oscillator.

The case considered above corresponds to a viscous damping force (the magnitude of

which is proportional to the velocity). In the case of a Coulombian dry damped force

(of constant magnitude during the motion), modelled physically as in Fig.8.31, the

equation of motion is of the form

sign 0xx x

+= 

(8.2.35)

and leads to

() ( )cos sin

xt x t t

δω ωδ

=± + ∓ ;

(8.2.35')

Dynamics of the particle in a field of elastic forces

507

we take

sign 1x =±

, denote by /

kδΦ

the displacement along the spring of elastic

constant

k due to the force of dry friction

and put the initial conditions (8.2.23').

We must study the motion piecewise after the direction of the velocity

x (in fact, on

semi-pseudoperiods). Without any loss of generality, we may assume that the particle

P starts from the point

P of abscissa

0x > without initial velocity (

0v = ); in

these conditions, the motion can take place if and only if the damping force is less than

the elastic force at the initial moment, hence if

kxφ

xδ

. The particle

begins to move with a negative velocity, so that its position is specified by

() ( )cos

xt x tδωδ=− +, 0/2tT

≤

≤ , till it reaches the point

P of abscissa

(2)

xxδ=− − , after a semi-pseudoperiod /2 /T πω

(when the velocity

() ( )sin

vt x tωδω=− − vanishes). If

0x > , then

x δδ

−

+<, the particle

remaining further in permanent rest; hence, if the stop point is at the same part as the

point of start (in particular, the initial position) with respect to the centre

O , then the

stopping is final. But if the point of stopping is situated on the other part of the centre

O , then the particle moves further as the condition

x δδ

−

> , hence the condition

x δ> is verified or not (Fig.8.32). If this condition is fulfilled, then the particle

continues to move with a positive velocity, in an interval of time equal to a new semi-

pseudoperiod, hence after the law

() ( 3 )cos

xt x tδωδ

−−, /2TtT≤≤ ,

which verifies the new conditions at the point

P , at the moment /2tT= , till the

point

P of abscissa

xx δ=−. An analogous reasoning is then made. Supposing

Figure 8.32. Coulombian damped linear oscillator. Trajectory.

that the conditions of motion are fulfilled, the particle reaches the point

P of abscissa

(1)( 2 )

xxnδ=− − after n semi-periods; the abscissae of this oscillatory motion

decrease in an arithmetic progression of ratio

−

. The motion ceases always after a

finite number of semi-pseudoperiods, let be

n semi-pseudoperiods. The particle passes

over the point

−

and stops at the point

P if

(2 1) (2 1)

nxnδδ

−

<< + . If

(2 1) 2

nxnδδ−<<, hence if

/2 1/2 1/2

nx nδ

+<+, then the point

is at the same part of the centre

as the point

−

, if

nxδ

(2 1)

n δ<+,

hence if

/2 1/2

nx nδ<<+, then the point

P is at the other part of the centre

as the point

−

, while if

xnδ

, hence if

nx δ

, then the point

P at

which the particle ceases to move coincides with the centre

. We denote

[

]

E/2

nxδ= and

[

]

E/2 1/2

nxδ

+ , where

[

]

E q represents the greatest

natural number contained in the number

; if

nnn

= , then the particle stops at

P ,

after

n semi-pseudoperiods, the centre

being contained in the interior of the segment of

a line

−

, if

1nn=+

, then

, and the particle stops after n semi-

MECHANICAL SYSTEMS, CLASSICAL MODELS

508

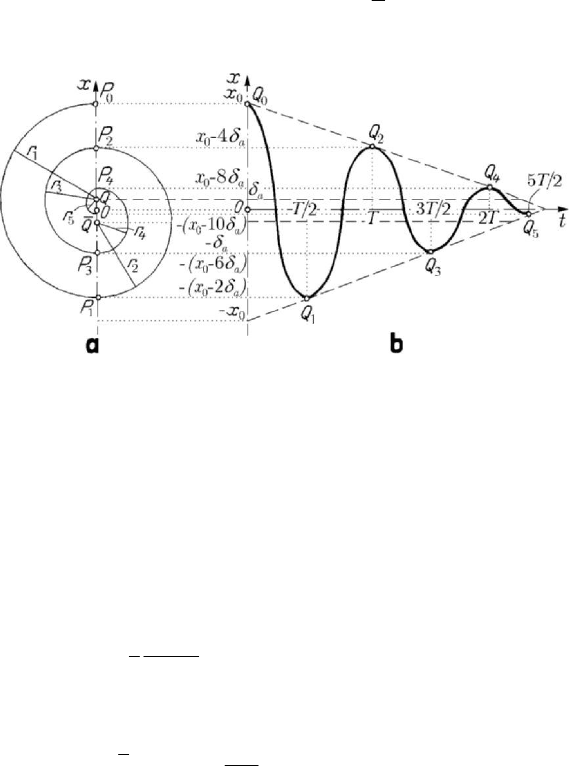
which decrease in arithmetic progression and of axes which differ by

δ∓

with respect

to the

Ot -axis, the motion ceasing when the amplitude is less than

δ (in Fig.8.33,b is

taken

5n = ); the points

,,QQQ and

,,QQQ of matching the arcs of cosinusoid

are collinear, respectively, but the straight lines

(4/)

xx tTδ

±− are not tangent

to those arcs at the respective points. We notice that the motion during each semi-

pseudoperiod may be obtained as a projection of a uniform circular motion on a

semicircle with the centre at

Q of abscissa

δ or at Q , of abscissa

δ− , and of radii

,,rrr or

,rr, respectively (Fig.8.33,a).

Figure 8.33. Coulombian damped linear oscillator. Trajectory as projection of circular

uniform motions on semicircles (a); diagram

()xt

vs t (b).

The damping by dry friction forces is, in fact, a particular case of non-linear

damping. Another important such case is that of a hydraulic damping force, in direct

proportion to the square of the velocity, which leads to an equation of the form

2sign 0xx xxλω++=   ;

(8.2.36)

proceeding as in Chap. 7, Subsec. 1.3.3, we may write the equivalent equation

(

)

2sign 0

xxx

λω



 ,

wherefrom we obtain the equation with separate variables

24sign

e(14sign)

xC x x

−

=+−





(8.2.36')

pseudoperiods at the point

P , on the same part as the point

−

with respect to the

centre

O , while if

nx nδ==, then the particle stops at the centre O , after an

interval of time equal to the respective number of semi-pseudoperiods. The diagram of

motion may be represented by a succession of arcs of cosinusoid, with amplitudes

Dynamics of the particle in a field of elastic forces

509

the constant

C being determined by the condition of vanishing the velocity at the

points where that one changes of direction. We notice that, replacing

x by x− and x

x−  , one obtains the same result; hence, the representation of the motion in the

phase space is symmetric with respect to the pole

O , the representation in the upper

semiplane being thus sufficient. Denoting

/8a ωλ= , CaC

, we may write for

the upper semiplane

(

)

[

]

2444

14 e e (4 1)e

xx x

va xC a C x

λλ λ

λλ

−

=−+ = − − .

(8.2.36'')

Figure 8.34. Hydraulic damped linear motion. Phase trajectory.

The points at which the phase trajectory pierces the

Ox -axis are given by the

equation

(4 1)e

λ −= (for 1C

− there is not one point, for 1C =− there

exists the crunode

0x = , for 10C

−

<< there exist the points

and

0x > ,

for

0C → there correspond

x →∞ and

1/4x λ→ , while for 0C ≥ there exists

only one point

1/4x λ≥ ). It results that for 10C

−

<< one obtains closed phase

trajectories, those ones having branches at infinity for

0C > . The separation curve is

the parabola

(1 4 )va xλ=− , corresponding to

(Fig.8.34).

2.2.7 Repulsive elastic forces. Self-sustained motions

In case of a repulsive elastic force of the form

()Fx kx

, 0k > , the equation of

motion is given by (we use the notations in Subsec. 2.1.2)

0xxω

−

= ;

(8.2.37)

with the initial conditions (8.2.23'), we obtain

MECHANICAL SYSTEMS, CLASSICAL MODELS

510

cosh sinh

xx t t

ωω

=+,

cosh sinhvv t x tωω ω

+ .

(8.2.37')

To fix the ideas, we assume that

0x > . If

0v > , then the particle travels through a

half straight line, starting from

P , in the positive direction of the Ox -axis

(Fig.8.35,a); the respective diagram of motion is given in Fig.8.35,b, the curve being

asymptotic to a hyperbolic cosine. If

0xvω

−

<<, then the particle starts from

P ,

reaches

A and

Figure 8.35. Particle acted upon by a repulsive elastic force; case

0v ≥ :

linear trajectory (a); diagram

()xt vs t (b).

then changes the direction of motion and tends to infinity in the positive sense of the

Ox -axis (Fig.8.36,a); the diagram of motion has a minimum

min

(/)xxvω=−

for

arg tanh( / )tvxω

′

=−, tending asymptotically to a hyperbolic cosine

(Fig.8.36,b). If

vxω<− , then the particle starts from

P , reaches O at the moment

Figure 8.36. Particle acted upon by a repulsive Figure 8.37. Particle acted upon by a

elastic force; case

0xvω−<<: repulsive elastic force; case

vxω<− :

trajectory (a); diagram

()xt vs t (b). trajectory (a); diagram ()xt vs t (b).

arg tanh( / )txvω

′′

=−, tending then to infinity in the negative sense of the

Ox -axis (Fig.8.37,a); the diagram of motion has a point of inflection at t

′′

on the

Ot -axis and tends asymptotically to a hyperbolic cosine (Fig.8.37,b). All these

motions are aperiodic and non-damped. If

vxω

− , then we obtain

(cosh sinh ) e

xx t t x

ωω

−

=−=, so that the particle starts from

and tends

asymptotically towards the centre

, the motion being damped (it is an interesting case

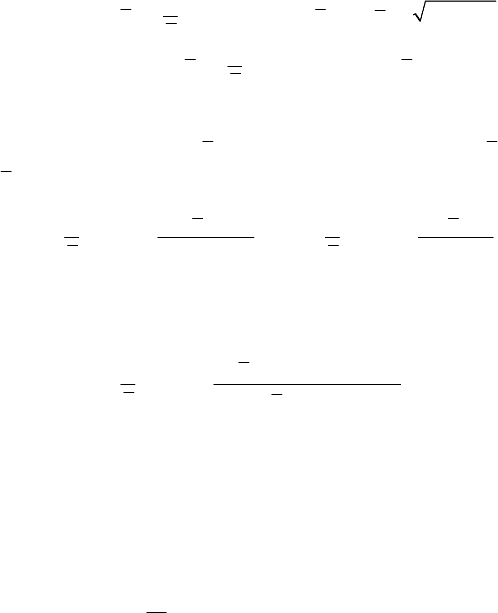
Dynamics of the particle in a field of elastic forces

511

of damping due to the initial conditions) and aperiodic (Fig.8.29,a); the diagram of

motion is of the same form as that in Fig.8.29,b.

If a viscous damping force intervenes too, then the equation of motion takes the form

20xxxλω

−= 

(8.2.38)

with the notations in Subsec. 2.1.3; with the same initial conditions, it results

000

() e cosh ( )sinh

xt x t v x t

ωλω

−

⎡⎤

=++

⎢⎥

⎣⎦

ωλω=+,

(8.2.38')

000

() e cosh ( )sinh

vt v t x v t

ωωλ ω

−

⎡⎤

=+−

⎢⎥

⎣⎦

(8.2.38'')

One obtains the same qualitative results for the trajectory and for the diagram of

motion, as

0v ≥ , as

() 0xvλω

−

+<<, as

()vxλω

−+ or as

()xλω=− + , respectively (Figs 8.35-8.37, 8.29); we observe that

arg tanh

λω

′

−

arg tanh

ωλ

−

′′

In what concerns the diagram in Fig.8.37,b, the point of inflection is no more on the

Ot -axis, but corresponds to

(

)

()

22 2

arg tanh

ωλ ω

λω λω

−

′′′ ′′

+−

In case of self-sustained motions of the particle, we use the considerations in Subsec.

2.1.4. For an elastic force of attraction, the equation of motion is of the form

20xxxλω

−

+=  .

(8.2.39)

We obtain

000

( ) e cos ( )sin e cos( )

xt x t v x t a t

λλ

ωλω ωϕ

⎡⎤

′′′

=+−=−

⎢⎥

′

⎣⎦

(8.2.39')

hence a subcritical damping (we assume that

ωλ> , hence

1χ

) for which the

pseudopulsation

′

is given by (8.2.15''), the pseudoperiod being 2/T πω

′

= . The

trajectory, which starts from the point

, has amplitudes more and more greater

(Fig.8.38,a), being thus modulated in amplitude; the diagram of motion has the aspect

of a cosinusoid contained between the curves

and tangent to them

(Fig.8.38,b). If

ωλ= (critical damping, 1χ

), we may write

[

]

00 0

() e ( )

xt x v x t

λ=+−

(8.2.39'')