Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

482

orbit for which

max

min

rrr≤≤ . To

max

min

rr r

= corresponds

max

; noting that

22 2

/2 /2mC r kr= , because

(

)

(

)

22 2

/2 /2mC r kr

/4mC k=

const

, it results

hmC Ckmkrω== =,

(8.2.3')

where we took into account (8.2.3) and we assumed that the motion takes place in the

positive sense of the angle

θ , so that 0C > . The extreme values of r are the roots of

the equation

[

]

() 2 () / 0rUrhmϕ =+= and are given by

222 2 2

max

22 2 2

min

11 11 11

hCmhmkChh

mh h h

⎛⎞⎛⎞⎛⎞

=±− =±−=±−

⎜⎟⎜⎟⎜⎟

⎝⎠⎝⎠⎝⎠

so that (

max

min

rr r= )

max

min

11 1 1

hhhhh

khkhh

⎛⎞

=±−= +±−

⎜⎟

⎝⎠

rh h

⎛⎞

=+±−

⎜⎟

⎝⎠

(8.2.3'')

the annulus which contains the orbit being thus specified.

Figure 8.9. Diagram ()Ur vs

, in case of an elastic force of attraction.

The trajectory is given by the relation (8.1.6''); choosing as

-axis the line of one

of the apocentres (

0θ =

), we have

Dynamics of the particle in a field of elastic forces

483

()

max

22 2

d1/

2 arccos

hCh

θπ

−

=− = −

⎛⎞ ⎛⎞

−

−− −

⎜⎟

⎝⎠

∫

where we took into account (8.2.3'), (8.2.3''). Hence, it results

1cos(2)11 sin

hh h h

ωθπ θ

⎧⎡ ⎤

⎪

⎛⎞ ⎛⎞

−+=+−

⎢⎥

⎨

⎜⎟ ⎜⎟

⎝⎠ ⎝⎠

⎢⎥

⎪

⎩⎣ ⎦

11 cos 1

hCh

θω

⎡⎤⎫

⎪

⎛⎞

+− − − = −

⎢⎥

⎬

⎜⎟

⎝⎠

⎢⎥

⎪

⎣⎦⎭

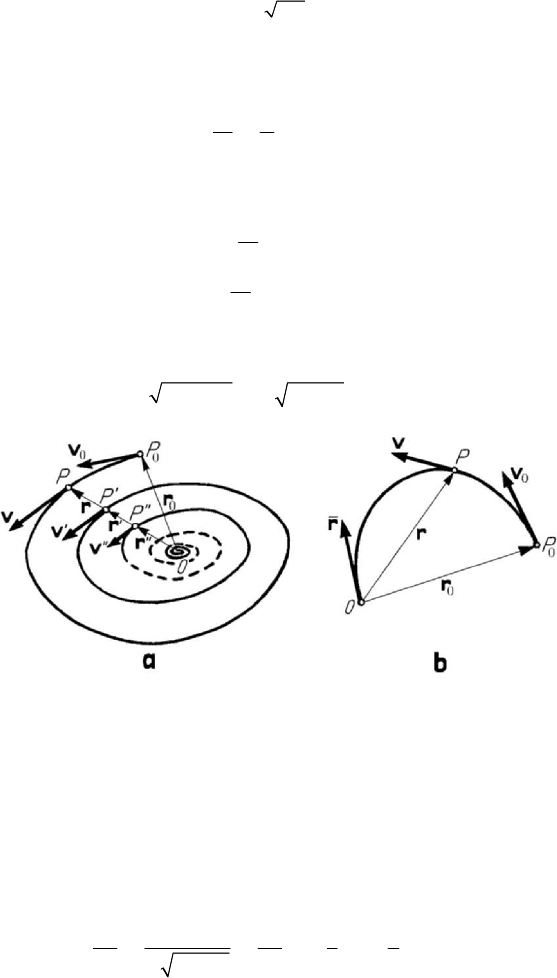
so that the orbit is an ellipse (Bertrand’s theorem is verified for this case) of equation

22 2

1cos sin

ra b

θθ

(8.2.3''')

Figure 8.10. Elliptic oscillator.

in polar co-ordinates; the semiaxes are

max

and

min

(Fig.8.10). The

mechanical system formed by a particle acted upon by an elastic force is called elliptic

oscillator.

The motion on the trajectory is specified by the first formula (8.1.6'''), wherefrom

(

0t =

)

(

)

1d 1

arctan tan

cos sin

ϑϑ

∫

where we noticed that

/(/)/(/)Cab hm hkωω

= . Taking into account (8.2.3'''),

we get the parametric equations of the elliptic orbit in the form

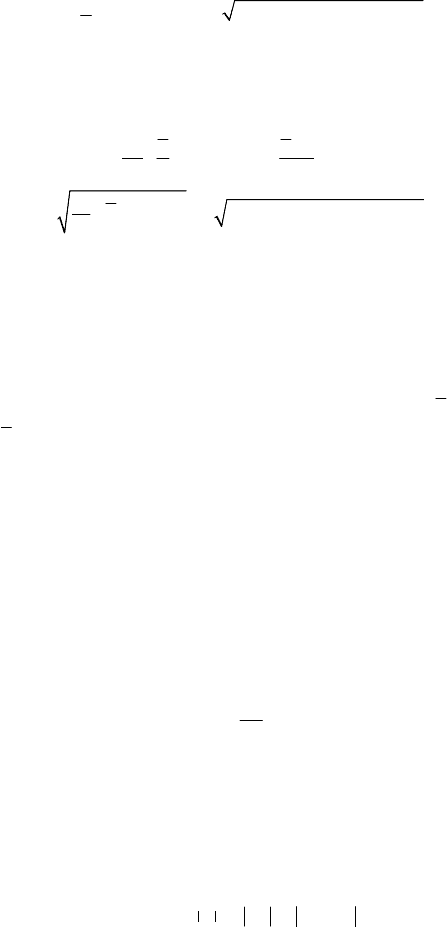
MECHANICAL SYSTEMS, CLASSICAL MODELS

484

(

)

arctan tan

θω=

22 22

cos sinra tb tωω

+ .

(8.2.4)

Using the first integral of areas and of mechanical energy, the components of the

velocity are given by

(

)

θω=



[]

()

2222 2

()

vr Urh v rr v

ω== + = + − −

(8.2.4')

where we took into account (8.1.6') and (8.2.3). We observe that the areal velocity is

expressed in the form

/2vΩδ= , where δ is the distance from the pole O to the

tangent to the trajectory at the considered point. Because

constΩ

, it results that

max

vv= for

min

rbδ == (at the extremities of the minor diameter), while

min

vv=

for

max

raδ == (at the extremities of the major diameter).

In case of the circular oscillator we have

max

min

rr r r

==, θω=



, 0

v = ,

vv r

ω== ; it results that ω is the angular velocity and the motion is uniform.

Starting from the expression (8.1.2) of the elastic force, we may write the equation of

motion (8.1.1) in the form



rr0,

(8.2.5)

where the pulsation

0ω > is given by (8.2.3). The initial conditions (

0t = )

(0)

rr,

(0)

(8.2.5')

lead to the solution of the problem in the form

() cos sintttωω

(8.2.5'')

() cos sintttωω ω

−vv r ;

(8.2.5''')

we notice that

×= ×rv r v, corresponding to the first integral of areas. The vector

r is a linear combination of the vectors

r and

v ; hence, the trajectory is a plane

curve, excepting the case in which the cross product mentioned above vanishes (the

vectors

r and

v are collinear). The trajectory does not pass through the origin

because

≠

r0, t∀ . We notice that

/ ω

≤

+rr v , t

∀

, so that all the points of

the trajectory are at a finite distance. Hence, the trajectory is a closed curve, which

surrounds the centre

O , that one being a stable position of equilibrium (the orbit can be

contained in the interior of a circle arbitrarily small, the velocity being arbitrarily small

too); the motion is periodic because the particle returns to the same position

(

()()tT t+=rr) with the same velocity ( ()()tT t

=vv), after the same period of

time

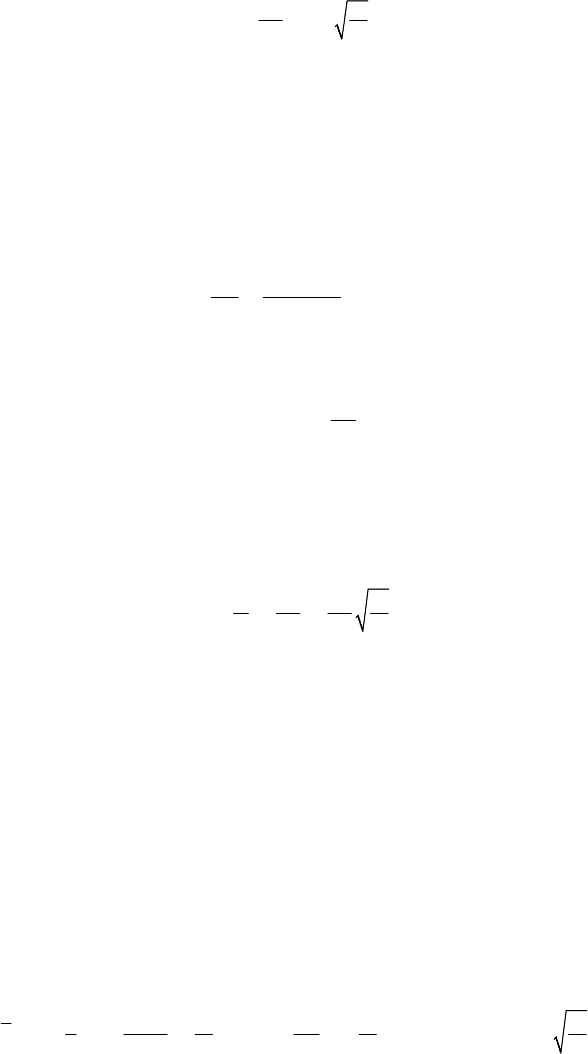
Dynamics of the particle in a field of elastic forces

485

== .

(8.2.6)

The pole

is a centre of symmetry of the trajectory and of the motion, because

(/2)()tT t+=−rr, (/2)()tT t

=−vv. The velocity vector is also finite; it is a

continuous function, which is non-zero for all values of

, so that the motion takes

place always in the same direction. With respect to a system of oblique co-ordinates

Ox x

′′

, specified by the conjugate diameters corresponding to the vector

r of the

initial position and to the initial velocity

v (Fig.8.10), one obtains the equation of the

ellipse in the form

()

v ω

′′

(8.2.7)

We notice that

()

222

00 0 0

cos 2 sin 2

tvr tωωω

⋅= ⋅ + −

rv r v .

Hence, to obtain a circular oscillator (

⋅

=rv , t

∀

) it is necessary and sufficient that

the initial conditions verify the relations

⋅

=rv and

vrω

The number which shows how many times the particle travels through the whole

trajectory in a unit time is called the frequency of the motion and is given by

ππ

== =

;

(8.2.6')

we notice that the pulsation

2ωπν

represents the number of periods in 2π units of

time, the denomination of circular frequency used too being thus justified.

These results may be easily correlate with those previously obtained starting from the

general theory of motion of a particle subjected to the action of a central force. We

observe that one obtains the same results as in the case of small motions of a spherical

pendulum around a stable position of equilibrium.

2.1.2 Case of a repulsive elastic force

In case of the motion around a labile position of equilibrium O , we consider a

repulsive elastic force of the form

verskr k==Frr, 0k > . (8.2.8)

The corresponding apparent potential is

()

222222

()

22 2

kmCm C m

Ur r r r

ωωθ

⎛⎞

=− = − = −

⎜⎟

⎝⎠



ω = ;

(8.2.9)

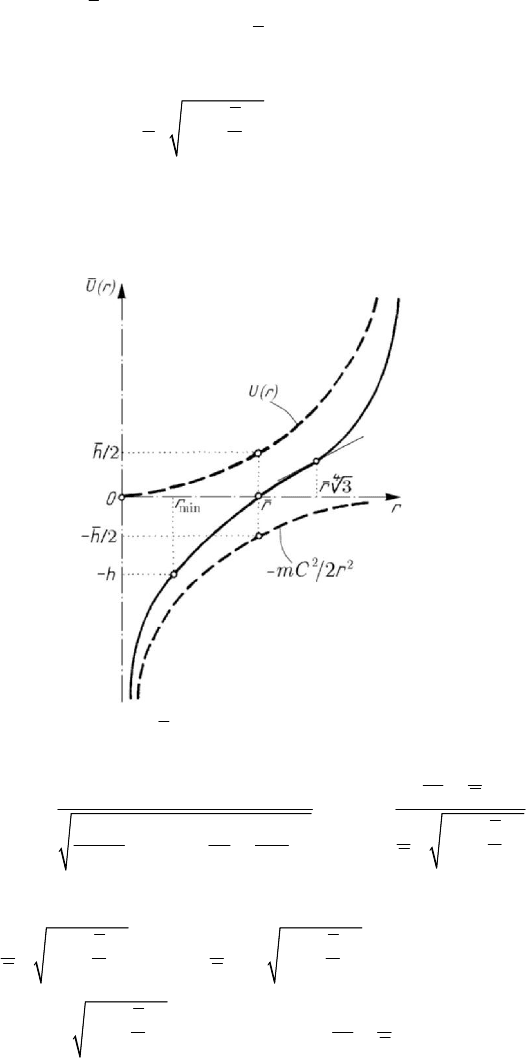
MECHANICAL SYSTEMS, CLASSICAL MODELS

486

the graphic of this function is represented in Fig.8.11, the radius

r and the

corresponding constant

h , given by the relations (8.2.3'), being put into evidence. In

case of a constant of energy

h for which ()Ur h≥− we obtain a unbounded orbit,

which has a pericentre given by (the positive root of the equation

() 0rϕ = )

min

⎡

⎤

⎛⎞

+−

⎢

⎥

⎜⎟

⎝⎠

⎢

⎥

⎣

⎦

(8.2.9')

We are in the case of Fig.8.6,b, the integrals (8.1.6''), (8.1.6''') being convergent (we

have

min

() ( ) ()rrr rϕψ=− ). Choosing as

Ox -axis the line of the pericentre

(

0θ = ), the formula (8.1.6'') leads to

Figure 8.11. Diagram ()Ur vs

, in case of a repulsive elastic force.

(

)

min

22 2

d1/

hCh

=−

⎛⎞

+− −

⎜⎟

⎝⎠

∫

arccos

−

⎛⎞

⎜⎟

⎝⎠

where we used the relations (8.2.3'), (8.2.9'). Hence, it results

1cos2 1 1cos

hh h h

ωθω θ

⎧⎡ ⎤

⎪

⎛⎞ ⎛⎞

+=++

⎢⎥

⎨

⎜⎟ ⎜⎟

⎝⎠ ⎝⎠

⎢⎥

⎪

⎩⎣ ⎦

11sin1

hCh

θω

⎡⎤⎫

⎪

⎛⎞

−+ − −=−

⎢⎥

⎬

⎜⎟

⎝⎠

⎢⎥

⎪

⎣⎦⎭

Dynamics of the particle in a field of elastic forces

487

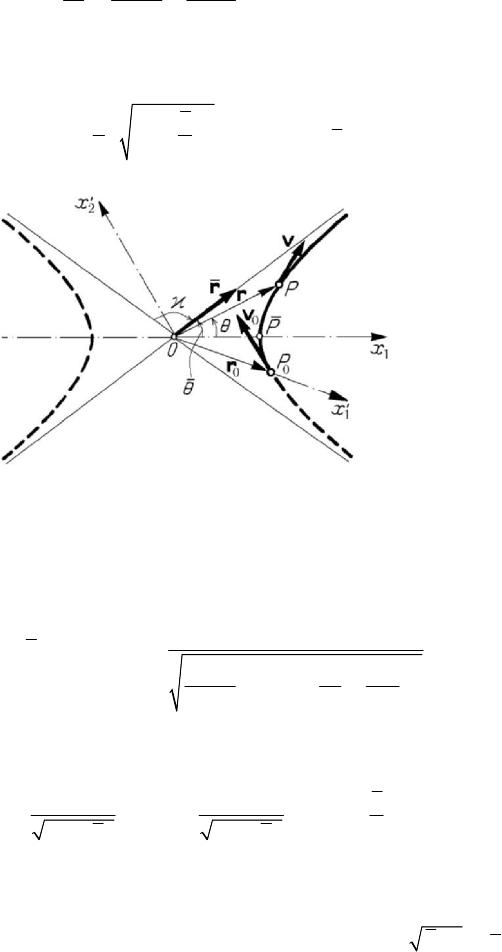
so that the orbit is an arc of hyperbola (Fig.8.12) of equation

22 2

1cos sin

ra b

θθ

=−

(8.2.10)

in polar co-ordinates; the semiaxes are given by

min

ar= ,

⎡

⎤

⎛⎞

=++

⎢

⎥

⎜⎟

⎝⎠

⎢

⎥

⎣

⎦

ab r

(8.2.10')

Figure 8.12. Trajectory of a particle acted upon by a repulsive elastic force.

The formulae (8.1.6''') allow then to study the motion of the particle along the

trajectory. We notice that we have to do with a phenomenon of diffraction, where the

angle of diffraction is given by

(

)

min

22 2

d1/

hCh

πθπ

=− =−

⎛⎞

+− −

⎜⎟

⎝⎠

∫



so that

22 22

arccos arccos arctan

hhh

hh hh

−

=− = =



(8.2.10'')

One observes that for

0h <

(hence

−

, we are above the

-axis) we have

ba<

and /2π>



, while for

0h >

(hence

−

, we are under the

-axis) we

have

ba> and /2π<



. For 0h

one obtains /ab hk r

== and

/2π=



, the hyperbola being equilateral (rectangular).

In case of the force (8.2.8), the equation of motion (8.1.1) has the form

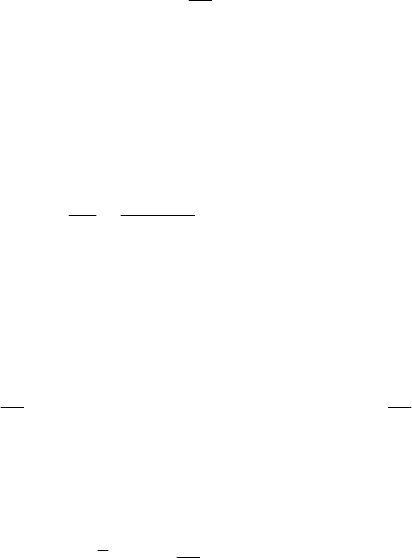
MECHANICAL SYSTEMS, CLASSICAL MODELS

488

−



rr0

(8.2.11)

If we put the initial conditions (8.2.5'), the solution of the boundary value problem is

given by

( ) cosh sinhtttωω

(8.2.11')

() cosh sinhtttωω ω=+vv r .

(8.2.11'')

With respect to the system of oblique co-ordinates

Ox x

′

, determined by the conjugate

diameters which correspond to the vector

r of the initial position and to the initial

velocity

v (Fig.8.12), it results that the trajectory is an arc of hyperbola of equation

(/)

rvω

′′

−

= ,

(8.2.12)

the centre

being a labile position of equilibrium (the orbit cannot be contained in the

interior of a circle arbitrarily small and the velocity of the particle may increase without

any limit). The particle travels through the trajectory only once without returning to the

initial position. We may write

(

)

() tanh coshtttωω

rr ,

(

)

() tanh coshtttωω ω

vr ;

noting that

lim tanh 1

tω

→∞

= , it results that the asymptote to which tends the trajectory

of the particle is specified by the vector

(8.2.12')

As in the case of an elastic force of attraction, these results may be easily correlate to

those previously obtained in the frame of the general theory of motion of a particle

subjected to a repulsive central force.

2.1.3 Motion of a particle subjected to the action of an elastic and of a damping

force

Let us suppose that in the motion of a particle subjected to the action of an elastic

force of attraction (8.2.2) intervenes a damping force

versΦ

− v

, tangent to the

trajectory and having a direction opposite to that of the motion. If the magnitude of the

damping force is proportional to the velocity, hence if

′

−



, 0k

′

> being a

damping coefficient, then the equation of motion becomes

2λω

 

rrr0

(8.2.13)

Dynamics of the particle in a field of elastic forces

489

with the constant

/2 0kmλ

′

=>. The damping coefficient corresponding to the

relation

ωλ

is a critical damping coefficient

′

; we notice that, in this case (

′

does not depend on

′

km kmω

′

== .

(8.2.14)

We introduce also the non-dimensional damping factor (the damping ratio, the critical

damping fraction)

′

(8.2.14')

With the initial conditions (8.1.5'), we get

000

() e cos ( )sin

tt t

ωλω

−

⎡⎤

′

=++

⎢⎥

′

⎣⎦

rr vr

(8.2.15)

000

() e cos ( )sin

tt t

ωωλω

−

⎡⎤

′

=−+

⎢⎥

′

⎣⎦

vv rv

(8.2.15')

where we have introduced the pseudopulsation

22 2

1ωωλωχ

′

=−=−,

(8.2.15'')

Figure 8.13. Damped pseudoelliptic oscillator (a); aperiodic damped motion (b).

assuming that

1χ <

, hence ωλ> (subcritical damping). The damping factor

λ−

transforms the trajectory which, in the absence of this factor, would be an ellipse in a

spiral (the radius vector diminishes continuously); the particle tends, in an infinite time,

to the origin

, with a velocity which tends to zero too (Fig.8.13,a). This mechanical

system is called also damped pseudoelliptic oscillator, the respective motion of the

particle being a pseudoperiodic damped motion. After equal intervals of time of

pseudoperiod

(

)

22213

1 ...

πππ

χχ

ωω

ωχ

== = + + +

′

−

MECHANICAL SYSTEMS, CLASSICAL MODELS

490

the particle reaches the points

′

, P

′

,…, which are situated on the common support

of the position vectors

′

,…; the corresponding velocities

′

v ,

′′

v ,… have the

same direction. We observe that

/ / ... e

rr rr

−

′′′′

===

, //vv vv

′

′′ ′

...=

Tλ−

= , obtaining a decrease in geometric progression of ratio e

Tλ

−

of the radius

vector and of the velocity; the number

(

)

2213

2 ...

πχπλ

δλ πχχ χ

=− =− =− =− + + +

′

−

is called logarithmic decrement (for

1χ  we may take 2Tλπχ

−

≅− ), being equal

ln( / ) ln( / ) ...rr vv

′′

==.

1χ = , hence if ωλ= (critical damping), then we may write

[

]

000

() e ( )

−

=++rrvr,

[

]

000

() e ( )

λλ

−

=−+vvvr.

(8.2.16)

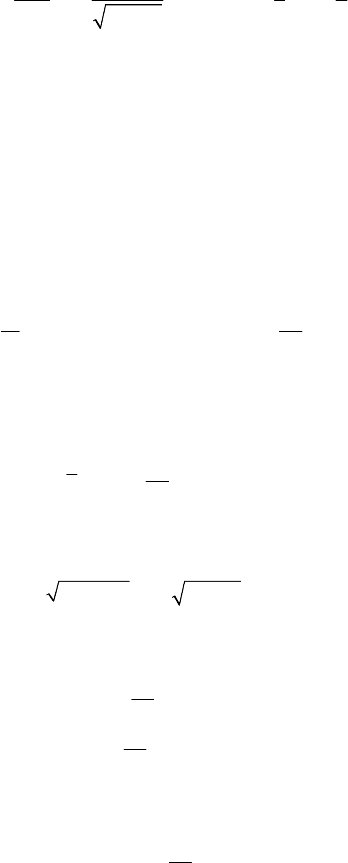
The corresponding motion is damped; the trajectory starts from the point

P and tends,

in an infinite interval of time, with a velocity which tends to zero, towards the centre

O , which is an asymptotic point (Fig.8.13,b). Noting that we may write

() e

−

⎡⎤

=++

⎣⎦

rvr

() e ( )

λλ

−

⎡

⎤

=−+

⎣

⎦

vvr

and that we have

lim e 0

λ−

→∞

, it results that the tangent at O to the trajectory is

specified by the vector

(8.2.16')

1χ > , hence if ωλ< (supercritical damping), then we use the notation

22 2

1ωλωωχ

′′

=−= −

(8.2.17)

and obtain

000

() e cosh ( )sinh

tt t

ωλω

−

⎡⎤

′

′′′

=++

⎢⎥

′′

⎣⎦

rr vr

(8.2.17')

000

() e cosh ( )sinh

tt t

ωωλω

−

⎡⎤

′

′′′

=−+

⎢⎥

′′

⎣⎦

vv rv

(8.2.17'')

Noting that we can write

000

( ) e cosh ( )tanh

tt t

ωλω

−

⎡

⎤

′

′′′

=++

⎢

⎥

′′

⎣

⎦

rrvr

Dynamics of the particle in a field of elastic forces

491

000

( ) e cosh ( )tanh

tt t

ωωλω

−

⎡

⎤

′

′′′

=−+

⎢

⎥

′′

⎣

⎦

vvrv

and that

()

lim e cosh lim e 1 e 0

ttt

λλωω

′′ ′′

−−−−

→∞ →∞

′′

=+=

lim tanh 1

tω

→∞

′′

it results that the trajectory of the particle has the same form as in the previous case

(Fig.8.13,b); the tangent at the asymptotic point

O will be specified by the vector

000

()λ

=+ +

′′

rr v r.

(8.2.17''')

Hence, the corresponding motion is strongly damped. We can say that both last

considered cases are aperiodic damped motions.

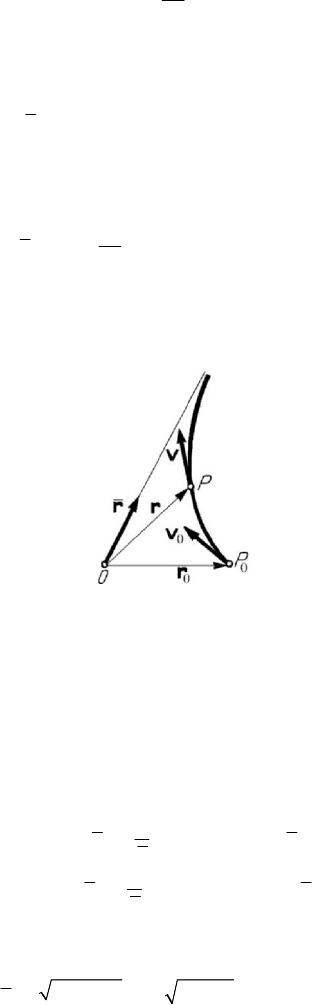
Figure 8.14. Aperiodic damped motion of a particle acted upon by a repulsive elastic force.

If the elastic force is repulsive, of the form (8.2.8), then the apparition of a damping

force the modulus of which is proportional to the velocity leads to the equation of

motion

2λω

−=

 

rrr0;

(8.2.18)

the initial conditions (8.2.5') lead to

000

() e cosh ( )sinh

tt t

ωλω

−

⎡⎤

=++

⎢⎥

⎣⎦

rr vr

(8.2.18')

000

() e cosh ( )sinh

tt t

ωωλ ω

−

⎡⎤

=+−

⎢⎥

⎣⎦

vv rv

(8.2.18'')

with the notation

22 2

1ωλωω χ=+=+.

(8.2.18''')

We observe that