Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

320

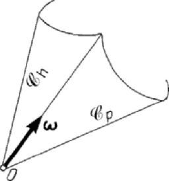
the points situated on the support of the angular velocity vector being of null velocity;

this support passes through the fixed point and is just the instantaneous axis of rotation

(in this case is no sliding). The axoids are two tangent cones, having the vertices at the

fixed point (Poinsot’s cones); the motion of a rigid solid with a fixed point is thus

characterized by the rolling without sliding of the polhodic cone

C (movable) over the

herpolhodic cone

C (fixed) (Fig.5.16).

Figure 5.16. Herpolodic and polodic cones of a rigid solid.

Introducing the components



, ϕ and θ



of the angular velocity with respect to the

axes

′

Ox and ON , respectively, (Fig.3.15), we may write

ψϕθ

′

=++





iinω ,

(5.2.34)

where

versON=

JJG

n . Projecting on the axes of the frame R, it results

cos sin sinωθϕψθϕ=+



sin sin cosωθϕψθϕ=− +



cosωϕψθ=+



(5.2.35)

while, in projection on the axes of the frame

′

R , we may write

cos sin sinωθψϕθψ

′



sin sin cosωθψϕθψ

′

=−



cosωψϕθ

′



(5.2.35')

If we put

x λω

′

and

x λω

, 1, 2, 3i

, then we obtain the parametric equations

of the herpolhodic and polhodic cones, respectively, the parameters being

λ and

To pass from

()

tω ,

1, 2, 3i

, to Euler’s angles ()tψ , ()tθ and ()tϕ , hence to

integrate the system (5.2.35) with respect to the latter unknown functions, it is useful to

introduce the intermediate unknown functions

()

tα ,

1, 2, 3i

, which represent the

direction cosines of the axis

′

with respect to the frame R. We have the relations

sin sinαθϕ=

sin cosαθϕ

cosαθ

, (5.2.36)

Kinematics

321

which allow the determination of Euler’s angles

ϕ , θ , if one knows

α ; the angle

is then obtained by a quadrature from the third relation (5.2.35). The link between the

functions

α and

ω is obtained writing that the derivative of the unit vector

′

i with

respect to the fixed frame of reference vanishes; we have

′′

×=



ii0ω ,

′

(5.2.37)

or, in components,

ijk k

αωα+∈ = , 1, 2, 3i

αα

. (5.2.37')

The distribution of accelerations is of the form

() ()ω=×+× × =×+ ⋅ −



ar r rr rωωω ω ωω

;

(5.2.38)

taking into account the results in Subsec. 2.1.2, we can state that – in general – in the

motion of a rigid solid with a fixed point, excepting the fixed point, there are not other

points of null acceleration. This motion is reducible to a motion of rotation only in the

case in which the vectors

ω and



are collinear or one of them vanishes.

2.3.4 Plane-parallel motion

We say that a rigid solid has a plane-parallel motion if three non-collinear points of

it are contained, during the motion, in a fixed plane (hence, if a plane section of the

rigid slides on a fixed plane). We notice that the motion of rotation and the motion of

translation, the trajectory of which is plane, are plane-parallel motions. Because each

point of a normal to the considered plane section has the same translated trajectory, we

may refer only to this plane section in the fixed plane. If the rigid solid is reduced to a

plate of small thickness (negligible), the median plane of which is just the fixed plane,

then the motion is called plane. We choose the two frames of reference so that the axes

′′

and Ox

, 1, 2α = , of the fixed and movable frames, respectively, be contained

in the fixed plane. In this case, the rigid solid has three degrees of freedom, and its

position at a moment

t can be specified by the scalar functions

()

xxt

αα

′′

, 1, 2α

, ()tθθ

(5.2.39)

where

′

are the co-ordinates of the pole O with respect to the fixed frame of

reference, while

θ is the angle made by the Ox

-axis with the

′

-axis (Fig.5.17).

The trajectories of the points of the rigid solid are, obviously, plane curves, while the

points situated on a parallel to the

′

-axis describe identical curves; hence, it is

sufficient to study the motion in the plane

Ox x

′

′′

, considered as a fixed plane. In this

case,

αα

′′′

vi,

αα

′

′′

ai,

′



(5.2.39')

Where, in the summation, the Greek indices take only the values 1 and 2.

MECHANICAL SYSTEMS, CLASSICAL MODELS

322

The formula (5.2.3) allows to write the distribution of the velocities in the form

11 2

vv xω

′′

=−

22 1

vv xω

′′

′

(5.2.40)

Figure 5.17. Plane-parallel motion of a rigid solid.

The points of null velocity of the rigid solid are given by

′

=−

′

= ,

arbitrary,

(5.2.41)

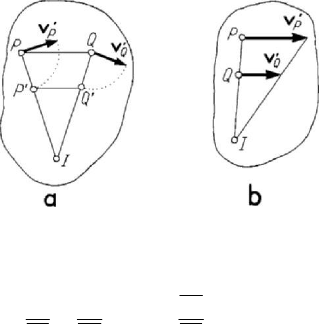
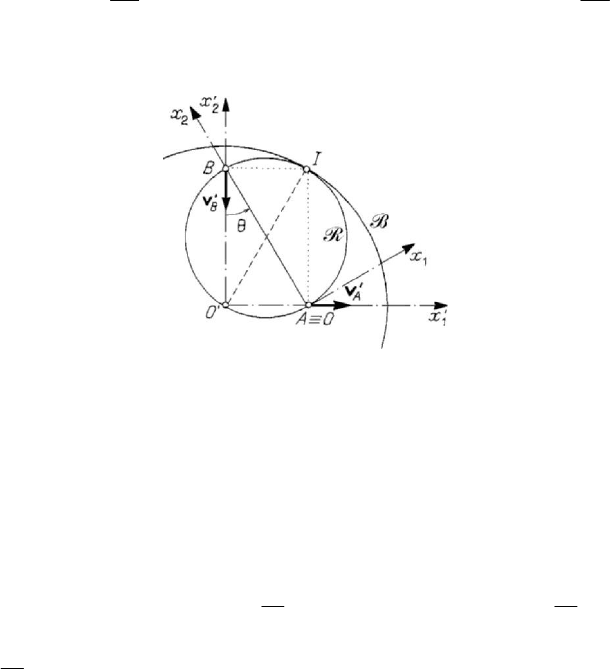
Figure 5.18. Fixed and movable centrodes in a plane-parallel motion.

with respect to the movable frame of reference, these points being situated on a straight

line normal to the fixed plane, which is the instantaneous axis of rotation (from the

given definition of the plane-parallel motion, it results that there is no sliding along this

axis). Hence, the rigid solid will be in instantaneous motion of rotation about an

instantaneous axis of rotation which is of constant direction and the trace of which on

the fixed plane is a point

I , called instantaneous centre of rotation; indeed, in this

plane (and in parallel planes too), an instantaneous motion of rotation of the points of

the rigid solid about the point

I (of null velocity) takes place, as it was shown by

Euler. The two axoids are, in this case, two cylinders, the traces of which on the fixed

plane are two curves: the basis B (the fixed (space) centrode) and the rolling curve R

Kinematics

323

(the movable (body) centrode), tangent at the instantaneous centre of rotation

(Fig.5.18). The velocities of the point

I in its motion with respect to the fixed and the

movable frames of reference are

′

v and

v , respectively; taking into account the

relation (5.2.32), it results

′

vv,

(5.2.42)

so that the two velocities are directed along the common tangent of the two centroids,

their elements of arc being equal. The plane-parallel motion of the rigid solid is thus

characterized by the rolling without sliding of the rolling curve over the basis.

The parametric equations of the rolling curve are, obviously, given by (5.2.41); by a

change of axes of co-ordinates, we obtain the parametric equations of the basis in the

form

111 2

cos sin

xξξθξθ

′

=+ − ,

221 2

sin cos

xξξθξθ

′

=+ + .

(5.2.43)

We notice that, at a moment

t , the velocity vector is normal to a radius starting from

the instantaneous centre of rotation and its modulus is proportional to the length of the

radius (an instantaneous motion of rotation about this centre takes place); hence, we

may use geometric methods to determine the point

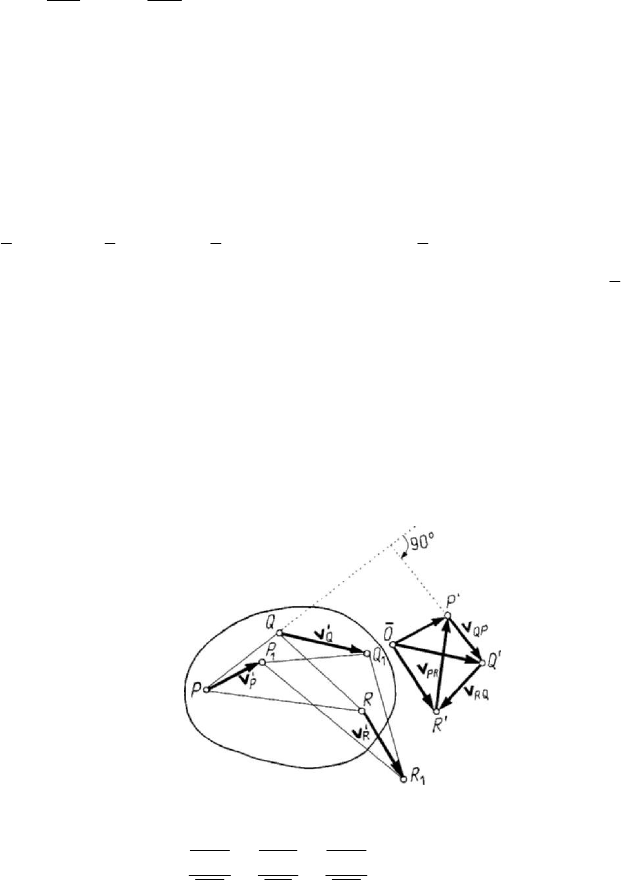
I and to draw the two centroids.

Thus, being given the velocities of two points

P and

of a rigid solid in a plane-

parallel motion (their non-parallel supports are sufficient), the centre

I will be at the

intersection of the normals to

′

v and

′

v at these points (Fig.5.19,a); it follows

Figure 5.19. Geometric determination of the instantaneous centre of rotation if one knows the

velocities of two points: concurrent velocities (a) or parallel velocities (b).

IP IQ

′

(5.2.44)

If the supports of the two velocities are parallel, then the centre

I is thrown to infinity,

′′

, and we have to do with a motion of translation. Finally, if the velocities

′

and

′

v are both normal to the straight line PQ , then the centre I will be on this line

at the point of intersection of it with the straight line which links the extremities of the

MECHANICAL SYSTEMS, CLASSICAL MODELS

324

two velocities (Fig.5.19,b). By turning down the vectors

′

v and

′

v in the same

direction of a rigid angle, we obtain the vectors

′

JJJG

and QQ

′

JJJG

, the points P

′

and Q

′

being on the straight lines

PI and QI , respectively (Fig.5.19,a); noting that

vPP

′′

= ,

vQQ

′′

= , and taking into account the relations (5.2.44) there results that

the straight line

′′

is parallel to the straight line PQ . Thus, the velocities turning

down method allows to construct graphically the velocity

′

of a point of a rigid

motion in a plane-parallel motion if we know the instantaneous centre of rotation

I , as

well as the velocity

′

v of another point P ; if

′

⊥

JJG

v , then we use the graphic of

Fig.5.19,b.

Let us consider the points

,,PQR,… in the plane section of the fixed plane, where

the velocity vectors

′

v ,

′

v ,

′

v ,… are applied; we construct the equipollent vectors

′′

JJJG

′′

JJJG

′

JJJG

,… at a pole O . We may introduce the relative

velocities

′′

JJJJG

′

JJJG

′

JJJJG

,… too; the figure OP Q R

′′′

…

forms the velocities plane. Taking into account the relation (5.2.3'), one obtains

(Fig.5.20)

QPQP

′′

=+vvv

PQ=×

JJG

v ω

(5.2.45)

We notice also that

PQ⊥

JJG

or PQ PQ

′′

⊥

JJJJG

JJG

and other analogous relations

(Fig.5.20). Introducing the moduli in the second relation (5.2.45) and proceeding

analogously with similar relations, we get

Figure 5.20. Velocities’ similarity theorem.

PQ QR RP

′′ ′′ ′′

==.

(5.2.45')

Hence, the triangles

PQR

′′′

and PQR are similar, their similarity ratio being ω ; we

notice that the sides of the triangle

PQR

′

′′

are normal to the homologous sides of the

Kinematics

325

triangle

PQR

. Because a polygon may be decomposed in a certain number of triangles,

we may state

Theorem 5.2.5 (the velocities’ similarity theorem; Burmester). If a polygon PQR …,

formed by the points of a rigid solid in plane-parallel motion is given, then the polygon

PQR

′′′

…, formed by the homologous points of the velocities plane, is similar to the

first polygon and is rotated through an angle of 90

with respect to this one in the

direction of the angular velocity.

Let be, e.g., a rigid bar

AB of length 2l , which is moving so that its extremities do

remain on the axes

′′

and

′

, respectively, hence on two fixed orthogonal

straight lines (Cardan’s problem) (Fig.5.21). We choose the pole of the movable frame

of reference in

OA≡ and the axis

Ox normal to AB ; the rigid solid has only one

degree of freedom, its position being specified by the angle

()tθ . The velocities of the

points

A and B will be along the fixed axes of co-ordinates, so that we may easily

determine the centre

I (2sinl θ , 2cosl θ ). We notice that the basis is a circle of centre

′

and radius 2OI l

′

= ; the rolling curve is a circle too, of diameter 2AB l= ,

passing through the points

′

and I . If the bar can stay only in the first quadrant, then

the basis is a quarter of a circle, while the rolling curve is a semicircle.

Figure 5.21. Cardan’s problem.

Let us consider also the case of a wheel of radius

R , which is moving on a

horizontal straight line (taken as axis

′

); we assume that the centre O of the wheel

moves with a horizontal velocity

′

v while this one rotates with an angular velocity

ω . The position of the wheel is given by two parameters; the abscissa

′

of the point

O and the angle θ specify a point of it, corresponding thus to two degrees of freedom

(the third one is annihilated by the imposed condition). The basis

B is a straight line,

parallel to the horizontal

′

and situated under the point O , while the rolling curve

is a circle

R of centre

and radius /

OI v ω

′

. If

vRω

′

, then OI R= , and

the motion of the wheel is a rolling without sliding (Fig.5.22,a). If

vRω

′

> , then we

have

OI R> , and the wheel slides in the direction in which it advances (the velocities

of all its points have the same direction; the case of the drawn wheel) (Fig.5.22,b); as

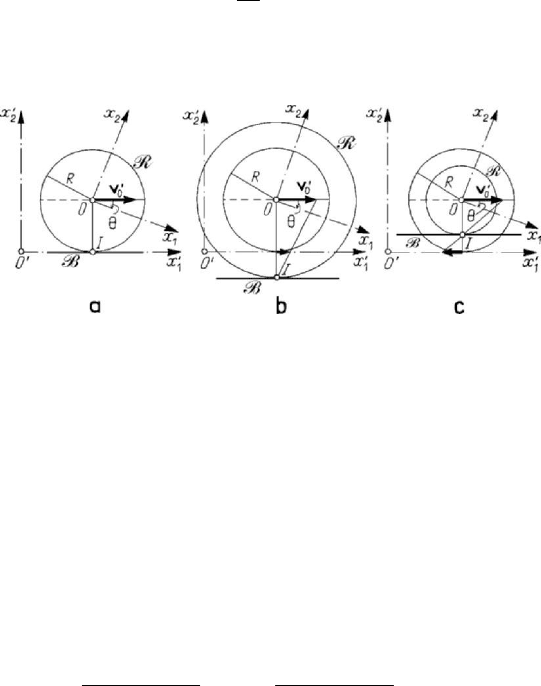
MECHANICAL SYSTEMS, CLASSICAL MODELS

326

well, if

vRω

′

< , then we see that

OI R

and the wheel slides in the opposite

direction to that in which it advances (there are points which have a direction opposite

to that of

′

v ; the case of the driving wheel) (Fig.5.22,c).

Figure 5.22. Motion of a wheel of a horizontal line: case

vRω

′

(a);

case

vRω

′

(b); case

vRω

′

(c).

The distribution of accelerations in the plane-parallel motion is given by the formula

(5.2.6) in the form (

0⋅=rω )

′′

=+×−



aa r rω ,

(5.2.46)

11 2 1

aa x xωω

′′

=−−



22 1 2

aa x xωω

′′

=+−



′

(5.2.46')

There exists a straight line parallel to

′

for which the accelerations vanish (



&ωω

corresponding to the considerations in Subsec. 2.1.2). The point

at which the

acceleration vanishes is called the centre (pole) of the accelerations, of co-ordinates

aaωω

ωω

′′

−



aaωω

ωω

′



(5.2.47)

with respect to the movable frame of reference. The instantaneous distribution of the

accelerations is identical to that of an instantaneous rotation about the centre

J , as one

can see effecting a change of axes in this pole.

We notice that the instantaneous centre

I and the pole of accelerations J are

distinct points, which do not coincide in the particular case of a motion of rotation.

Hence, in general,

′

=v0

′

≠

a0 and

′

≠

v0,

′

a0.

We have seen that the instantaneous centre may be used to determine the velocities

of some points of the rigid solid, when one of these velocities is known; we notice that

the pole of accelerations

J can play an analogous rôle to determine the accelerations.

In the method of the accelerations’ pole we suppose known the acceleration

′

of the

point

P , the angular velocity

and the angular acceleration



ω . Thus, starting

from the point

P , we draw the segment PJ , which makes the angle given by

tan /ϕωω=



, in the direction indicated by the angular acceleration, with the

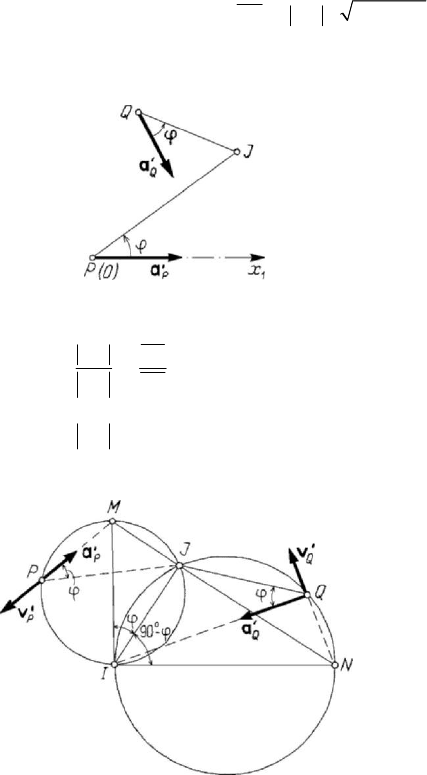
Kinematics

327

acceleration

′

, the point J being specified by

PJ ωω

′



(Fig.5.23);

indeed, if

OP≡ and one takes the

Ox -axis along the vector

′

a , then the formulae

(5.2.47) justify the above affirmation. Noting that

Figure 5.23. Method of the acceleration’s pole.

′

(5.2.48)

we may easily draw the vector

′

a applied at the point Q , which makes an angle ϕ

(in the same direction as that indicated by the angular acceleration) with

JQ .

Figure 5.24. Inflections and turning back circles.

In a plane-parallel motion, the locus of the points

P for which

′′

×=va 0

is a

circle (called the inflections circle), while the locus of the points

for which

′′

⋅=va

is a circle too (called the turning back circle). If we draw from I the

orthogonal straight lines which make the angles

ϕ and 90 ϕ°− with IJ and meet the

normal to

IJ at J in M and N , respectively, then the circles of diameters IM and

IN , respectively, are the searched loci (the circles of Bresse); the drawing easily

justifies this assertion (Fig.5.24).

To the points

,,PQR,…, of accelerations

′

a ,

′

a ,

′

a ,…, correspond the

equipollent vectors

′′ ′

JJJG

′

′′

JJJJG

a ,

′

′′

JJJG

,…, applied at the point O

′

;

MECHANICAL SYSTEMS, CLASSICAL MODELS

328

the figure

OPQR

′′′′

… constitutes the plane of accelerations (Fig.5.25). Introducing

the relative accelerations

()

QP Q P

P Q PQ PQ

′′ ′ ′

==−=×+××

JJJJG

JJG JJJG



aaaωωω,…,

(5.2.49)

Figure 5.25. Accelerations’ similarity theorem.

as sums of two terms which have the same expressions as in case of the circular motion,

we may state (as in the case of velocities)

Theorem 5.2.6 (the accelerations’ similarity theorem). If a polygon PQR …, formed

by points of a rigid solid in plane-parallel motion is given, then the polygon

PQR

′′′

…,

formed by the homologous points of the accelerations plane is similar to the first

polygon and is rotated through an angle of

180 ϕ°− with respect to this one in the

direction of the angular acceleration.

The relations

PQ QR RP

′

′′′′′

(5.2.50)

take place for the triangles

PQR and PQR

′

′′

. We mention that the similarity theorem

and the relation (5.2.50) remain valid also in the case of collinear points

,,PQR (to

these points correspond the collinear points

,,PQR

′

′′

in the accelerations plane).

The velocities plane and the accelerations plane lead to methods useful for the

graphical computation to determine the corresponding kinematic quantities.

Let

111

,,PQ R

,… be the extremities of the velocity vectors

′

v ,

′

v ,

′

,…, applied

at the points

,,PQR

,…, respectively (Fig.5.20). We may write

QP QP

P Q PQ PQ PQ PQ

′′

=+−=+ =+×

JJJG JJJG JJJG JJJG JJJG

vv v ω

;

noting that the vector product

PQ×

JJG

is a polar vector normal to PQ

JJG

and contained

in the plane of motion, and taking into account that the vector

is normal to this

plane, it results

Kinematics

329

(

)

()

22 2

1P Q PQ PQ PQω=+× =+

JJG

Completing the similarity theorem (for velocities) we may state that the polygons

PQR

… and

111

PQ R … are similar too, the similarity ratio being

1 ω+ (as well

with the polygon

PQR

′′′

…).

If, analogously,

111

,,PQ R

… are the extremities of the acceleration vectors

′

a ,

′

,…, applied at the points

,,PQR

,…, respectively (Fig.5.25), we may write

QP QP

P Q PQ PQ PQ PQ PQω

′′

=+−=+ =+×−

JJJG JJJG JJJG JJJG JJJG JJJG



aa a ω

where we took into account the formula (5.2.46); as above, we notice that the vector

product

PQ×

JJG



is a polar vector, normal to PQ

JJG

, contained in the plane of motion,

and taking into account that the vector



is normal to this plane, we obtain

()

(

)

()

22 2

222

11P Q PQ PQ PQωωω=− + × = − +

⎡⎤

⎣⎦

JJG



ω .

Hence, completing the similarity theorem (for the accelerations), we may state that the

polygons

PQR … and

111

PQ R

… are similar too, the similarity ratio being

()

1 ωω−+



(the same statement with the polygon PQR

′

′′

…).

We can emphasize also some interesting properties concerning the displacement of a

segment of straight line

PQ in a plane-parallel motion. Let be the segments PQ and

RS in the positions

PQ and

RS , at the moment

t , and in the positions

PQ and

RS , at the moment

t , respectively, with respect to a fixed frame of reference.

Taking into account a property emphasized in Subsec. 2.1.1, we may write

(

)

11 11

,PQ R S =

JJJG JJJJG

)

(

)

22 22

,PQ R S

JJJJG JJJJJG

)

; noting that

(

)

11 22

,PQ PQ

JJJG JJJJJG

)

(

)

11 11

,PQ R S

JJJG JJJJG

)

(

)

11 22

,RS RS++

JJJG JJJJJG

)

(

)

22 2 2

,RS PQ

JJJJG JJJJJG

)

and taking into account the previous relation, we

get

(

)

(

)

12 1 1 2 2 1 1 2 2

,,PQ PQ R S R Sθ ==

JJJG JJJJJG JJJJG JJJJJG

))

(5.2.51)

We may thus state

Theorem 5.2.7. In a plane-parallel motion, the angle

θ formed by two homologous

segments of straight line at the moments

t and

t depends only on the two moments,

but not on the two considered segments (being thus equal to the angle formed by any

other two homologous segments of straight line at the same moments).

0θ

, then we have

11 22

PQ PQ

JJJG JJJJJG

; but

11 22

PQ PQ=

JJJG JJJJJG

so that

12 1 2

PP QQ=

JJJG JJJJJG

these vectors defining a motion of finite translation. If

0θ

≠

we construct a point