Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

330

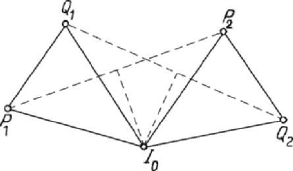
at the intersection of the midperpendiculars of the segments

PP and

QQ (Fig.5.26).

Noting that the triangles

IPQ and

IPQ are equal (their sides are equal, by

construction), it results

11 22

PI Q PI Q= ; we may thus write

12 12

PI P Q I Q= too, so

that the segment of straight line

PQ can be superposed over the segment of straight line

PQ by a finite rotation about the point

I . We may state

Figure 5.26. Euler’s theorem for a plane-parallel motion.

Theorem 5.2.8 (Euler). In a plane-parallel motion of a rigid solid one may pass from a

position corresponding to a moment

t to a position corresponding to a moment

t by

a finite translation or by a finite rotation.

tt→ , then the point

I becomes the instantaneous centre of rotation.

In a general motion of the rigid solid, we construct the vectors

′′ ′

JJJG

v ,

′′ ′

JJJJG

v and

′′ ′

JJJG

v equipollent to the velocities of the points ,,PQR at an

arbitrary point

O . The points ,,PQR

′

′′

determine a plane Π on which we project the

points

,,PQ and R ; the projections of the corresponding velocities

′

JJG

v ,

′

JJJG

v and

′

JJJG

v are the vectors

JJG

. As it was shown by

Poncelet, the normals at the points

,,pq

and r to these projections on the plane

respectively, are concurrent; the instantaneous axis of rotation and sliding passes

through this point and is normal to the considered plane.

3. Relative motion. Kinematics of mechanical systems

Starting from the results concerning the relative motion of a particle, we pass to the

relative motion of a mechanical system, in particular of a rigid solid. We give then some

results concerning the systems of rigid solids.

3.1 Relative motion of a particle

We analysed till now the motion of a particle P with respect to a fixed frame of

reference

′

R of axes

123

Ox x x

′′′ ′

; sometimes, it is useful to consider its motion with

respect to a frame of reference of axes

123

Ox x x in motion with respect to the fixed

frame (a movable frame

R) (Fig.5.27). It is thus put the problem to determine the

kinematic quantities which characterize the motion of the particle with respect to the

Kinematics

331

frame

′

R if the quantities corresponding to the motion of the particle with respect to

the frame

R, as well as the motion of R with respect to

′

R are known. Such a

problem is important – for instance – in the study of the motion of a particle on the

surface of the Earth.

Figure 5.27. Relative motion of a rigid solid.

The motion of the particle with respect to the fixed frame of reference is called

absolute motion, its motion with respect to the movable frame of reference being the

relative motion; the motion of transport characterizes the motion of

R with respect to

′

R and can be specified by the motion of its pole and of its axes. The velocities and

accelerations are called absolute, relative and of transport, after the motions to which

these quantities correspond. The mechanical phenomenon in its totality is called relative

motion. We assume that the time

t is the same in the two frames of reference (the

Newtonian model). Eventually, we may have

consttt

′

+ ; the constant can be taken

equal to zero, without losing something of the generality of the phenomenon.

In what follows, we consider the composition laws of velocities and accelerations in

the case of a particle, emphasizing thus the basic kinematic laws of the relative motion.

3.1.1 Composition of velocities

Starting from the relation (5.2.1) which links the position vectors r and

′

of the

particle

with respect to the frames R and

′

R , respectively, we differentiate with

respect to time in the fixed frame of reference. Applying the formula (A.2.37) which

links the absolute derivative (with respect to

′

R ) to the relative derivative (with

respect to

R), we may write

∂

+×

∂

rω

(5.3.1)

Noting

′

∂

′

+×vv r

(5.3.2)

MECHANICAL SYSTEMS, CLASSICAL MODELS

332

where

v ,

v and

v are the absolute velocity, the relative velocity and the velocity of

transport of the particle, respectively; we obtain

+vvv

(5.3.3)

and may state

Theorem 5.3.1. The absolute velocity of a particle is obtained by the vector

composition of the velocity of transport with the relative velocity of it.

Equating to zero the relative motion (

v0), we notice that the velocity in the

motion of transport is – as a matter of fact – the velocity of a point of the rigid solid,

rigidly linked to the movable frame of reference.

3.1.2 Composition of accelerations

Differentiating the relation (5.3.3) with respect to time in the frame

′

R and taking

into account (5.3.2) and (A.2.37), we may write

ddd

ttt

ddd d

ttt t

′

=+×+×

∂

+×

∂

Using the formula (5.3.1) and the notations

∂

, 2

×av

()

′

=+×+××



aa r rωωω,

′

(5.3.4)

where

a ,

a and

a are the absolute acceleration, the relative acceleration, the

acceleration of transport and the acceleration of Coriolis (the complementary

acceleration) of the particle, respectively, we obtain

++aaaa; (5.3.5)

noting that the absolute acceleration is not obtained by summing vectorially the

acceleration of transport with the relative acceleration (by vanishing the motion of

transport, a complementary term, due to Coriolis, is added to the relative acceleration),

so that we state

Theorem 5.3.2. The absolute acceleration of a particle is obtained by the vector

composition of the acceleration of transport with the relative and Coriolis’

accelerations.

Excepting the trivial case in which

v0, the acceleration of Coriolis vanishes if

= 0ω , hence if the movable frame of reference has a motion of translation with

respect to the fixed frame of reference (the movable frame is not rotating, its axes

having a displacement parallel to themselves), or if

(e.g., the case of a particle

in motion on the generatrix of a right circular cylinder, which rotates about its axis).

Kinematics

333

As it can be easily verified, after Resal, if

′

′′

ωω or if

rrr

′′′

vvv,

corresponding to two successive rotations or relative motions, then the resultant

acceleration of Coriolis is the sum of the component Coriolis’ accelerations

(

CCC

′′′

aaa).

As in the case of velocities, by equating to zero the relative motion (

==va0),

we notice that the acceleration in the motion of transport is the acceleration of a point of

the rigid solid, rigidly linked to the moving frame of reference.

We may apply the above results – for instance – to the computation of the velocities

and of the accelerations in polar, cylindrical, or spherical co-ordinates, by the

composition of rectilinear motions or of motions of rotation, hence by the composition

of a motion of transport with a relative one.

3.2 Relative motion of the rigid solid

The results obtained at the preceding section may be used in the study of the motion

of a point of an arbitrary mechanical system, hence in the study of the motion of the

respective mechanical system. In particular, we consider the relative motion of the rigid

solid, emphasizing the corresponding composition of the velocities and of the

accelerations.

3.2.1 Composition of velocities

Let us consider a fixed frame of reference

R of pole O , a moving frame of

reference

R of pole

O and another moving frame of reference

R of pole

O ,

rigidly linked to the rigid solid. In this case, the relative velocity (with respect to the

movable frame of reference) of a point

P of the rigid solid is given by

21 21 2

=+×vv rω , where

v is the velocity of the pole

O with respect to the pole

O ,

ω is the angular velocity of the frame

R with respect to the frame

R , while

r is the position vector of the point P with respect to the frame

R ; using analogous

notations, we may write the velocity of transport (of the moving frame with respect to

the fixed one) in the form

10 10 1

+×vv r

. The formula (5.3.3) of composition of

velocities allows to write the absolute velocity (of the point

P with respect to the frame

R ) in the form

10 21 10 1 21 2

=++×+×vvv r r

ω . (5.3.6)

In the case of

1n −

motions of transport, corresponding to

−

frames

R ,

R ,…,

1n −

R , the frame

R being fixed, while the frame

R is rigidly linked to the

rigid solid, we may write

,0 ,0

,1 ,1

nn i

ii ii

−−

=+×= + ×

∑∑

vv r v rωω,

(5.3.7)

MECHANICAL SYSTEMS, CLASSICAL MODELS

334

the formula being proved by complete induction, taking into account (5.3.6) too;

analogously, the angular velocity of the rigid solid with respect to the fixed frame

is given by

−

∑

ωω ω .

(5.3.7')

In particular, if all the component motions (both relative and of transport) are

translations, then we obtain (

10 21 , 1

...

nn−

== =0

ωω)

−

∑

vv,

(5.3.8)

all the points of the rigid solid having the same velocity. We may state

Theorem 5.3.3. By the composition of n motions of translation of a rigid solid one

obtains a resultant motion which is a motion of translation too, the velocity of a point of

the rigid solid being equal to the vector sum of the velocities of translation of the

component motions.

If all the component motions are instantaneous rotations and if the origins of the

corresponding frames are on the instantaneous axes of rotation and coincide, then we

have (

10 21 , 1

...

nn−

== =vv v 0,

...

== =rr r r)

×vr

−

∑

ωω

(5.3.9)

and we may state

Theorem 5.3.4. By the composition of n instantaneous motions of rotation, the

instantaneous axes of rotation of which are concurrent at a fixed point

O , one obtains

an instantaneous resultant motion which is also an instantaneous motion of rotation

about an instantaneous axis of rotation which passes through the same point

O and the

angular velocity of which is the vector sum of the angular velocities of the component

motions.

This result allows the study of the motion of a rigid solid with a fixed point, by the

composition of three instantaneous motions of rotation about three instantaneous axes

of rotation, passing through the fixed point.

In the case of instantaneous motions of rotation about some instantaneous parallel

axes of rotation, we may write (

,1ii−

v0,

,1 ,1ii ii

−−

, 1

u , 1,2,...,in= )

=×v ωρ, ω= uω ,

−

∑

u ω ,

−

∑

ρ ,

(5.3.10)

assuming that

≠ 0ω . We may pass from a point

to a point Q by the relation

OQ OP PQ=+

JJJG JJJJG JJJG

, wherefrom

Kinematics

335

()

PQ PQωω

−

=× + = + ×

∑

JJG JJJG

vu r v u ;

= 0ω , then we obtain

vv, hence a motion of translation. We may thus state

Theorem 5.3.5. By the composition of n instantaneous motions of rotation, the

instantaneous axes of rotation of which are parallel, of angular velocities

,1ii−

ω , one

obtains an instantaneous resultant motion which is an instantaneous motion of rotation

about an instantaneous axis of rotation passing through the centre of the parallel

vectors

,1ii

−

ω of angular velocity

−

∑

ωω,

or a motion of translation, as we have

≠

, respectively.

If, for

2n =

, we have

10 21

= 0

, then we can say that a couple of

instantaneous rotations is equivalent to a translation.

In the general case, by passing from a point

to a point Q of the rigid solid, we

obtain a relation of the same form as that above, i.e.

PQ=+×

JJG

vvω

(5.3.11)

(of the form (5.2.27)). We attach the relation

,1 ,1

ii ii

−

=+×

∑∑

JJJG

vv ω

(5.3.7'')

to the relation (5.3.7'), so that we can introduce the torsor of the angular velocities,

applying the static-kinematic analogy. The considerations made in Subsec. 2.3.1 remain

valid, and we may classify the resultant instantaneous motions (obtained by the

composition of some instantaneous motions), as in the case of only one such motion.

In particular, for rest with respect to a fixed frame of reference we must have

, (5.3.12)

the point

being arbitrarily chosen.

Observing that

(

,1 ,1 ,1 1 1 1 2

11 1

...

nn n

ii ii ii i i i

ii i

OP OO O O

−− −+++

== =

×= × = × +

∑∑ ∑

JJJG JJJJJJJG JJJJJJJJJG

rωω ω

)

()

11012102123

... ...

OO OP OO OO

−

++=×++×

JJJJJJJG JJJJG JJJJJGJJJJJG

ωωω

...

−

⎛⎞

+×

⎜⎟

⎝⎠

∑

JJJG

ω ,

≡

MECHANICAL SYSTEMS, CLASSICAL MODELS

336

0,0

,1 1

ii i

OO O P

−

−+

=+×+×

∑∑

JJJJJJG JJJJG

vv ωω,

(5.3.13)

an useful relation for practical applications. If we take into account a formula of the

form (5.3.11), then we get

,0 ,0

,1 1

nii

ii i

−

=+×

∑∑

JJJJJJG

vv ω .

(5.3.13')

The general motion of a rigid solid is completely characterized by the vectors

()t

′

and ()tω , corresponding to a motion of translation and of rotation, respectively; as we

have seen, the vector

()vt

′

may be replaced by a couple of vectors

()tω ,

()t−ω .

Using the general results given in Chap. 2, Subsec. 2.2.4, concerning the systems of

sliding vectors, we can state

Theorem 5.3.6. The general motion of a rigid solid at a given moment may be obtained

by the composition of three instantaneous motions of rotation about three instantaneous

axes of rotation passing through three given points or by the composition of two

instantaneous motions of rotation about two instantaneous axes of rotation, one of them

passing through a given point.

We notice that the relation (5.2.31) established for a point of the instantaneous axis

of rotation and sliding corresponds, in fact, to the basic formula (5.3.3) in a relative

motion. We come back to the respective problem in the particular case of a plane-

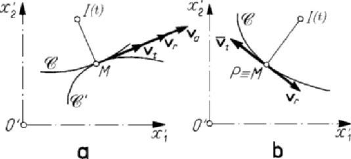
parallel motion, considered in Subsec. 2.3.4. Let thus be the instantaneous centre of

rotation

I ( ()It at the moment t ), which describes the curve B (basis) in the

absolute motion, and the curve

R (rolling curve) in the relative motion, respectively;

obviously, its velocity vanishes (

v0) in the motion of transport. The formula

(5.3.3) leads thus to

=vv, so that the two centrodes are tangent at ()It at the

moment

t . In modulus, we have ss

′

 too, so that () ()st st

′

on the curves B and

R, respectively; we start from the initial moment

at which the two centrodes are

tangent at

()It and which is considered to be the origin for the corresponding

curvilinear co-ordinates. We may thus state

Theorem 5.3.7. In the plane-parallel motion of a rigid solid, the basis B and the

rolling curve

R are centrodes tangent at ()It at the moment t ; during the motion,

the rolling curve is rolling without sliding over the basis.

We may also state

Theorem 5.3.7' (reciprocal). If in a plane-parallel motion a smooth curve R, rigidly

linked to the rigid solid, is rolling without sliding over a fixed smooth curve

B, then the

point of contact

()It of the two curves at the moment t is the instantaneous centre of

rotation,

B and R being the basis and the rolling curve, respectively.

Indeed, at the point

()It we have

vv, λ scalar, and ss

′

=, so that

=vv; the relation (5.3.3) leads – in this case – to

v0, condition which

we may also write

Kinematics

337

characterizes the centre

()It . If we enlarge somewhat the conditions of this reciprocal

theorem so that, in general,

′

≠

, then 1λ

≠

; on the basis of the relation (5.3.3), the

velocity

≠v0 is along the common direction of the velocities

and

, hence it is

tangent to the two curves at the point

M , while ()It is on their common normal

(Fig.5.28,a). We thus state

Figure 5.28. Properties of a smooth curve rigidly linked to a rigid solid

in a plane-parallel motion.

Theorem 5.3.8. If, in a plane-parallel motion, a smooth curve C, rigidly linked to the

rigid solid, remains all the time tangent to a smooth fixed curve

′

C , then the

instantaneous centre of rotation

()It is, at any moment

, on the common normal at

the point

of contact.

Let also be a curve

C, rigidly linked to a rigid solid, which passes through a fixed

point

M , and let be a point P on this curve, which coincides all the time with the

point

; the point

describes the curve C with respect to the movable frame of

reference, remaining at a fixed point with respect to the fixed frame of reference.

Hence, at this point

=v0 and

=vv 0; but

v is along the tangent at P to the

curve

C, so that

v enjoys the same property (Fig.5.28,b). It results that the centre I is

on the normal to this tangent and we may state

Theorem 5.3.9. If, in a plane-parallel motion, a smooth curve C, rigidly linked to the

rigid solid, passes all the time through a fixed point

M , then the instantaneous centre

of rotation

()It is at any moment t on the normal at M to the curve C.

3.2.2 Composition of accelerations

As in the case of the distribution of velocities, we consider a fixed frame of reference

R of pole

, a movable frame

R of pole

and a frame

R of pole

, rigidly

linked to the rigid solid. The relative acceleration (with respect to the movable frame)

of a point

of the rigid solid is given by

21 21 2 21 21 2

()

+×+× ×



aa r r

ωω ,

where

a is the acceleration of the pole

with respect to the pole

ω and



are the angular velocity and acceleration, respectively, of the frame

R with respect to

the frame

R , while

r is the position vector of the point

with respect to the frame

R ; using analogous notations, we may write the acceleration of transport (of the

movable frame with respect to the fixed one) in the form

10 10 1

=+×



aa rω

MECHANICAL SYSTEMS, CLASSICAL MODELS

338

10 10 1

()+× ×rωω . The acceleration of Coriolis is given by

=×avω

10 21 21 2

2( )=×+×vrωω. The formula (5.3.5) of composition of accelerations allows

to write the absolute acceleration (of the point

P with respect to

R ) in the form

10 21 10 1 21 2 10 10 1

()

=++×+×+× ×



aaa r r r

ωωω

21 21 2 10 21 21 2

()2( )+× ×+ × + ×rvrωω ω ω .

(5.3.14)

In the case of

1n − motions of transport, corresponding to 1n

−

frames

R ,

R ,…,

1n −

R , the frame of reference

R being fixed, while the frame

R is rigidly

linked to the rigid solid, we have

,0 ,0 ,0 ,0

,1 ,1

()

nn n n i

ii ii

−−

=+×+× ×= + ×

∑∑



aa r r a rωωω ω

,1 ,1 , 1 ,1 ,1

121

()2 ( )

nni

ii ii jj ii ii

iij

−

−− −−−

===

+××+ ×+×

∑∑∑

rvrωω ω ω

;

(5.3.15)

the formula may be proved by complete induction, taking into account the relation

(5.3.14) and the sum (5.3.7'). Differentiating the last formula with respect to time in the

fixed frame of reference, we may write

,0 ,1 ,1

dd d

nii ii

tt t t

−−

−

∂

⎛⎞

== = +×

⎜⎟

∂

⎝⎠

∑∑

ωω

,1 , 1 ,1

111

nni

ii j j ii

iij

−

−−

===

=+ ×

∑∑∑



ωωω,

so that the angular acceleration of the rigid solid with respect to the fixed frame

will be given by

,1 , 1 ,1 ,1 1,0 ,1

121 12

nni nn

ii j j ii ii i ii

iij ii

−

−−−−−−

=== ==

== + × = + ×

∑∑∑ ∑∑

  

ωω ω ω ω ω ω ω

(5.3.15')

In particular, if all the component motions (both of transport and relative) are

translations, we obtain (

,1 ,1ii ii−−



0ωω , 1,2,...,in

)

−

∑

aa,

(5.3.16)

all the points of the rigid solid having the same acceleration, and we may state

Theorem 5.3.10. By the composition of n motions of translation of a rigid solid, one

obtains a resultant motion which is a motion of translation too, the acceleration of a

Kinematics

339

point of the rigid solid being equal to the vector sum of the accelerations of translation

of the component motions.

If all the component motions are instantaneous rotations, the origins of the

corresponding frames of reference being on the instantaneous axes of rotation and being

coincident, we get (

,1ii−

=v0,

,1ii−

a0,

rr,

1,2,...,in

)

,1 ,1 ,1 , 1 ,1

11 21

()2 ()

nn ni

ii ii ii j j ii

ii ij

−

−−− −−

== ==

⎛⎞

=×+××+ ××

⎜⎟

⎝⎠

∑∑ ∑∑



ωωω ωωar r r;

(5.3.17)

noting that, in general,

≠



, even if the component rotations are uniform

(

,1ii−



0ω , 1,2,...,in= ), we may state that, by the composition of n instantaneous

motions of rotation, the instantaneous axes of which are concurrent at a point

, one

obtains a motion with a distribution of accelerations characteristic to a rigid solid with a

fixed point (the point

In the case of some instantaneous motions of rotation about some parallel

instantaneous axes of rotation, we can write (

,1 ,1jj ii−−

= 0

ω , , 1,2,...,ij n= )

−

∑



ωω,

(5.3.18)

the vector



ω being parallel to the vector

; we obtain as resultant motion an

instantaneous rotation about an instantaneous axis of rotation or a translation, the

distribution of accelerations being a corresponding one.

Noting that

112 1

...

iii n

OO O O O O O P

+++ −

=+ ++ +

JJJJJJG JJJJJJJJJG JJJJJJJJG JJJJG

r , taking into account

(5.3.7') and (5.3.15'), and using the relation

1,0 ,1 1,0 ,1 ,1 1,0

() ()()

ii i

i ii i ii ii i

−− − − −−

×+=××−××rr rωω ω ω ω ω ,

a consequence of the relation (2.1.50'), we may write the law of composition (5.3.15)

also in the form

,0 ,0

,1 1

ii n

ii i

OO O P

−+

=+×+×

∑∑

JJJJJJG JJJJG



aa ωω

,0 ,0 ,0 ,0

11,0,1

()()2

iii nn

iiii

OO O P

−

+−−

+×× +××+ ×

∑∑

JJJJJJGJJJJG

vωω ω ω ω

(5.3.19)

useful in many applications.

In the general case, passing from a point

to a point Q of the rigid solid, we

obtain a relation of the form

()

PQ PQ=+× +××

JJG JJJG



aaωωω,

(5.3.20)