Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

300

(

)

(

)

ii i

tt=+−−Vv v ,

1,2,...,in

(5.1.34')

represents the jump of the velocity, corresponding to the moment of discontinuity

tt= , while the sign “tilde” is for the derivative in the usual sense; we may thus state

Theorem 5.1.2. The acceleration of a particle in the sense of the theory of distributions

is equal to the distribution defined by the acceleration of the particle in the usual sense,

where the latter one exists, to which is added the sum of the products of the velocity

jump, of the particle by the Dirac distribution.

We introduce the notations

d()

()

d()

()



()

ttt

=δ−

∑

aV,

(5.1.34'')

where

()ta is the acceleration in the sense of the theory of distributions, ()t



a is the

acceleration in the usual sense, while

()

ta is the complementary acceleration due to

the discontinuities. With these notations, the relation (5.1.34) becomes

() () ()

tt t



aaa.

(5.1.34''')

The acceleration in the sense of the theory of distributions will be called generalized

acceleration too.

1.3 Particular cases of motion of a particle

We consider, in what follows, some particular cases of motion: the rectilinear

motion, the circular motion, the parabolic motion, the helical motion, as well as the

cycloidal motion.

1.3.1 Parabolic and rectilinear motion

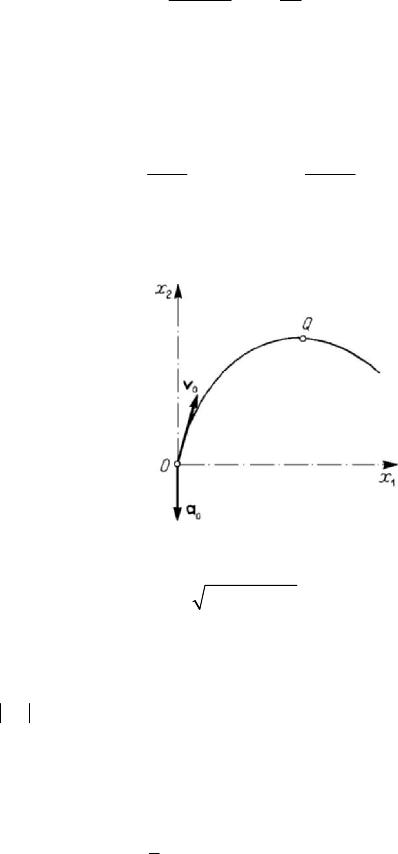
We consider the particular case

const==

JJJJG

aa ; integrating, we get

(

)

00 0

tt=− +vav,

() ()

00 000

tt tt

−+−+ravr

(5.1.35)

where we have supposed that

vv and

rr at the initial moment. We notice that,

taking a new origin of the frame of reference at

rr, nothing of the generality of the

trajectory is lost; the position vector

r is thus a linear combination of the constant

vectors

v and

a , hence, it belongs to a fixed plane, so that the trajectory is a plane

curve. We suppose that the trajectory is contained in the plane

Ox x ; we may thus

write the parametric equations in the form (Fig.5.6)

()

()xt v t t=−,

() ()

22 2

()

xt a t t v t t=−+−

(5.1.35')

where

Kinematics

301

where, for the sake of simplicity, we take the

Ox -axis along the acceleration

a .

Eliminating the time

t , we get

()

211

xxx

;

(5.1.36)

hence, the trajectory is a parabola, the axis of which is parallel to the acceleration

a ;

the vertex

Q of the parabola is of co-ordinates (we notice that

v ,

0v > ,

0a < )

=−

()

2max

=−

(5.1.36')

and is obtained by the particle at the moment

/tt va=− . We may write

Figure 5.6. Parabolic motion of a particle.

222max

2vax=− ,

(5.1.37)

obtaining thus Torricelli’s formula, which gives the component

v of the initial

velocity of the particle which attains the ordinate

2max

x , assuming an acceleration of

modulus

a=−a . These results stay at the basis of studies on external ballistics.

In the particular case in which

, the motion is rectilinear; if we assume that

the motion is along an

Ox -axis, then the second relation (5.1.35') allows to write the

equation of motion (which is – at the same time – the horary equation) in the form

()()

00 000

() ()

xt st a t t v t t x== −+ −+

(5.1.38)

where we put into evidence the initial position (eventually another one that the origin

O ); there results

(

)

000

()vt a t t v

−+.

(5.1.38')

MECHANICAL SYSTEMS, CLASSICAL MODELS

302

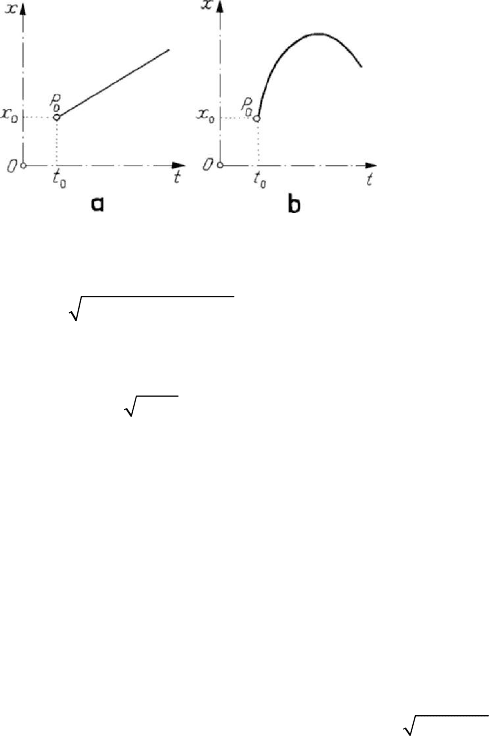
, then the motion is uniform and the diagram of motion is given in

Fig.5.7,a. As a matter of fact, the reciprocal implication is also true; indeed, if

=a0,

then

=vv,

(

)

000

−+rv r,

(5.1.39)

the trajectory being a straight line. If

≠

, then the motion is uniformly varied;

eliminating the time

t between the relations (5.1.38), (5.1.38'), we obtain Torricelli’s

formula in the form

Figure 5.7. Diagram of a rectilinear motion of a particle: uniform (a)

and uniformly varied (b).

()

00 0

2vvaxx=+ −;

(5.1.40)

in particular, if the particle has not initial velocity at the origin

O , then we get

2vax= .

(5.1.40')

If, for a certain interval of time, the velocity and the acceleration have the same

direction, then the motion is accelerated, on the contrary, the motion is decelerated. In

the case of a varied motion, it is possible to have both phases (for instance, a motion the

diagram of which is given in Fig.5.7,b) or only one of them.

1.3.2 Circular motion

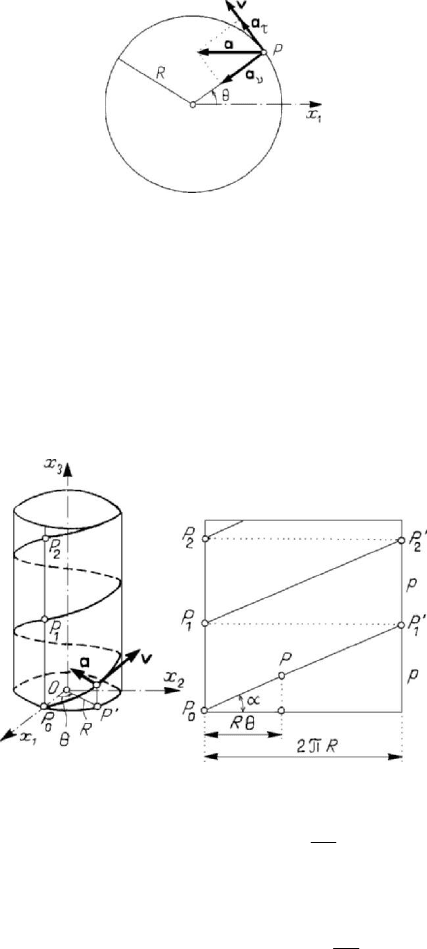
If the trajectory is a circle of radius R (

ri), then the motion is called circular

(Fig.5.8). By means of the formulae (5.1.7), (5.1.19) or of the formulae (5.1.14),

(5.1.28), we obtain

=×ωvr,

vv v sR

===

sR sθ

, (5.1.41)

ω=×−



ωarr,

aaR



aaR

ω=− = ,

aRωω=+



(5.1.41')

where we have introduced the angular velocity

ω and the angular acceleration ε ,

defined by the relations

Kinematics

303

() ()ttω

ω i ,

() () ()tttω



εω i , () ()ttωθ=



, () () ()tttεωθ==





(5.1.42)

Figure 5.8. Circular motion of a particle.

0ω =



constω =

(and

constv

), then the motion is uniform and we have

tθω θ=+,

(

)

sRtωθ=+, vRω

, 0a

aa R

ω==

(5.1.43)

1.3.3 Helical motion

Let be a particle in a uniform motion on a helix of pitch 2tanpRπα

, situated on

a circular cylinder of radius

R (Fig.5.9). The trajectory is given by

Figure 5.9. Helical motion of a particle.

cosxR tω= ,

sinxR tω

(5.1.44)

Hence,

sinvR tωω=− ,

cosvR tωω

(5.1.45)

MECHANICAL SYSTEMS, CLASSICAL MODELS

304

cos

=+=

;

(5.1.45')

then

cosaR tωω=− ,

sinaR tωω=− ,

(5.1.46)

and

aRω=

(5.1.46')

Thus, the motion is uniform and the acceleration is reduced to the normal

acceleration given by (5.1.20). Comparing to (5.1.46') and taking into account (5.1.45'),

we obtain the radius of curvature

4cos

πα

=+ = ;

(5.1.47)

the principal normal is parallel to the plane

Ox x and passes through the

Ox -axis;

hence, the acceleration

enjoys the same property (as it results from the formulae

(5.1.46)).

1.3.4 Cycloidal motion

Another interesting particular case of motion is that of a particle P on a cycloid; that

one is the locus of a point of a circle (for instance, on the peripheral of a wheel in a

vertical plane) of radius

R , which is rolling without sliding on a straight line

(horizontal) (Fig.5.10). The imposed condition leads to

Figure 5.10. Cycloidal motion of a particle.

tθω

ω =

(5.1.48)

where

const=

JJJJG

v is the velocity of the centre O

′

of the circle, supposed to have a

uniform motion. The parametric equations of the trajectory are

so that

Kinematics

305

(sin)xRt tωω=− ,

(1 cos )xR tω

− ,

(5.1.49)

wherefrom one obtains the components of the velocity and of the acceleration

(1 cos )vR tωω=− ,

sinvR tωω

(5.1.49')

sinaR tωω= ,

cosaR tωω= ,

(5.1.49'')

respectively.

One can easily prove that the modulus of the velocity and of the acceleration are

expressed in the form

2 sin 2 sin

vR v AP

ωω

===,

aR OPωω

′

(5.1.49''')

respectively; the acceleration

is directed towards the centre O

′

of the circle. Hence,

from the point of view of the velocities, the particle behaves as in a uniform motion of

angular velocity

ω around the point A ; what concerns the accelerations, it behaves as

in a rotation around the point

′

2. Kinematics of the rigid solid

In the study of the motion of a rigid solid, it is necessary to study the motion of an

arbitrary point

P of it with respect to a fixed frame of reference

′

R of orthogonal

Cartesian co-ordinates

123

Ox x x

′′′ ′

. By means of some basic kinematics formulae which

are deduced, one considers some particular cases of motion; hence, one can pass to the

general case of motion of the rigid solid.

2.1 Kinematical formulae in the motion of a rigid solid

We put in evidence, in what follows, some results concerning the determination of

the velocity and the acceleration in the motion of a rigid solid.

2.1.1 Velocity in the motion of the rigid solid

Let be a movable frame of reference R of orthogonal Cartesian co-ordinates

123

Ox x x , in a rigid linkage with the rigid solid (hence, in motion with respect to the

fixed frame of reference

′

R , specified by the constant unit vectors

′

i , 1, 2, 3j = );

obviously, we use right orthonormed frames of reference. We denote by

′

r the

position vector of the pole

O with respect to the pole O

′

and by

′

′′

ri the position

vector of the point

with respect to the frame

′

R ; analogously, the position vector

of the same point

with respect to the movable frame of reference is

x=ri, where

i , 1, 2, 3j = , are the unit vectors of the frame R (Fig.5.11). We mention that, during

the motion,

const=

JJJJG

r with respect to the moving frame R. We notice that the latter

frame can be determined by the vector

r and the unit vectors

i , 1, 2, 3j = (as a

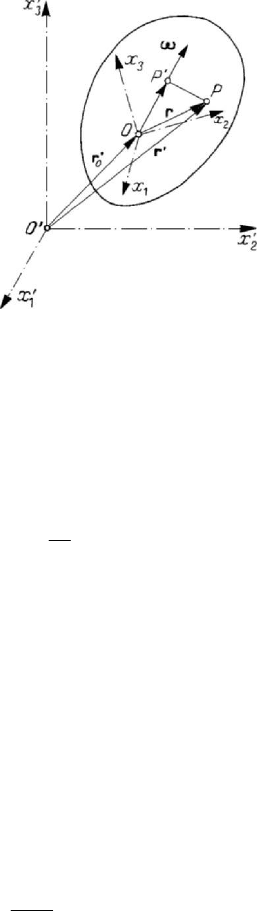
MECHANICAL SYSTEMS, CLASSICAL MODELS

306

matter of fact, one of the unit vectors and the plane formed by the other two unit vectors

are sufficient), that is 2+1=3 independent scalar quantities; this result corresponds to the

six degrees of freedom of the rigid solid. The position of the point

P with respect to

the frame

′

R is given by

Figure 5.11. Motion of the rigid solid with respect to a fixed and

a movable frame of reference.

′

+rrr.

(5.2.1)

Using the formula (A.2.37) which links the absolute derivative (with respect to the

frame

′

R ) to the relative derivative (with respect to the frame R ), we may write

=×



(5.2.2)

where

ω is a vector specified by (A.2.36), the same for all the points of the rigid solid

(hence, an invariant); we took into account that the derivative of

r with respect to the

movable frame of reference is equal to zero (

/ t

∂

∂=r0). For the velocity

′′



the point

P with respect to the fixed frame of reference we obtain Euler’s formula,

which gives the distribution of the velocities in a rigid solid

′

+×

vv r,

(5.2.3)

where we have introduced the velocity

′



vr of the pole O of the frame R with

respect to the same frame

′

R . We notice that the relations (5.2.2), (5.2.3) may be

written in the form

=×

JJG

ω ,

(5.2.2')

′′

−

+× =

JJG

ωvv 0

(5.2.3')

Kinematics

307

too, where

O and P are two arbitrary points of the rigid solid. Scalarly, we have

ii j

ijk k

vv xω=+∈ , 1, 2, 3i

(5.2.3'')

A scalar product of the relation (5.2.3) by

vers r leads to a mixed product which

vanishes, so that

vers vers

′′

⋅

=⋅vrv r;

(5.2.4)

hence, the projections of the velocities of two points of a rigid solid on the straight line

which links these points are equal. We notice that the relation (5.2.4) corresponds to the

relation (3.2.22'), a consequence of the rigidity condition (3.2.22), and represents the

condition of compatibility of the velocities in the motion of the rigid solid (relation of

holonomic constraint).

Let

P and

P be two points of the rigid solid. From the relation

12 2 1

P P OP OP=−

JJJG JJJJGJJJG

, it results

222

12 1 2 1 2

2P P OP OP OP OP=+−⋅

JJJG JJJG JJJJG JJJG JJJJG

; hence, the

condition of rigidity of the solid (

constPP =

JJJG

constOP =

JJG

constOP =

JJJG

)

leads to

(

)

,constOP OP =

JJG JJJJG

)

. We may thus state that the angle of two arbitrary

segments of a rigid solid is conserved in a general motion of it.

Analogously, effecting the scalar product of the relation (5.2.3) by the vector

, we

get

′

⋅

=⋅

ωvv

(5.2.5)

and may state

Theorem 5.2.1. The scalar product of the velocity of a point of the rigid solid by the

vector

is an invariant (the same for all the points of the rigid solid).

We can state also that the projection of the velocity of a point of the rigid solid on the

vector

ω is a constant (the same for all the points of the rigid solid). It follows that, in

the case of a general motion (for

′

v and

arbitrary vectors), there are not points of

vanishing velocity (for which

′

v0). We obtain this result also by observing that the

equation

′

+×=ωvr0 has a solution only if

′

⋅

v ; as well, if the vectors

′

and

ω are orthogonal at a point, then they are orthogonal at any other point.

Hence, in the motion of the rigid solid do appear two kinematic invariants: the vector

ω as we will see in Subsec. 2.2.2, it is an angular velocity) and the scalar product

⋅ ωv

(or the projection of the vector

on the direction of the vector

, that is

/ ω⋅ ωv ).

2.1.2 Acceleration in the motion of a rigid solid

Differentiating the relation (5.2.3) with respect to time in the frame

′

R , we obtain

the acceleration with respect to the same frame

MECHANICAL SYSTEMS, CLASSICAL MODELS

308

()

′′

=+×+××



ωωaa r r

(5.2.6)

where we have introduced the acceleration

′



of the pole O of the movable

frame of reference with respect to the same fixed frame; we took into account the

formula (5.2.2) and the relation

d/d /tt

=∂ ∂



ωω (on the basis of the formula

(A.2.37)). Using the basic formula of the triple vector product (2.1.49), we may write

()ω

′′

=+×+⋅ −



ωωωaa r r r

(5.2.6')

too; in components, we have

(

)

ii ij ij j

ijk k

aa xωω ω δ ω

′′

=+ − −∈



, 1, 2, 3i

(5.2.6'')

Denoting by

′

the projection of the point P on the vector ω (we have

OP OP P P

′′

== +

JJJGJJJJG

JJG

) and noting that

′

JJJG

ω 0

in (5.2.6) and

0PP

′

⋅=

JJJG

(5.2.6'), we obtain Rivals’ formula

OP P Pω

′′ ′

=+× −

JJJG

JJG



ωaa .

(5.2.6''')

Imposing the condition

′

, 1, 2, 3i

, we get a system of linear equations in

the co-ordinates

, obtaining thus the points in which the acceleration of the rigid

solid vanishes. If we use the formula (2.1.36''), then we may write the determinant of

the coefficients of the unknowns of this system in the form

(

det

ij ij i

ijk k ijk lmn l il

Δωωωδ ω ωωωδ=−−∈=∈∈−

⎡⎤

⎣⎦



)

(

)

(

)

pm qn r

jjmjmq

ilp k kn knr

ω ωω ωδ ω ωω ωδ ω−∈ − −∈ − −∈



;

developing, we obtain 27 sums of products, seven of them being equal to zero, because

they correspond to products of symmetric tensors by antisymmetric ones with respect to

the same indices. Taking into account the formulae (2.1.46)-(2.1.46'') and the above

observation, we get

222 2

() ( )

ijij iijj

Δ ωωωω ωωω ω ω ω=−=⋅−=−×



  

ωωω,

(5.2.7)

where we have used Lagrange’s identity (2.1.33).

×≠



ωω 0 , then there exists a point (and only one), called the pole of

accelerations, for which the acceleration vanishes at a given moment; hence, this pole

is moving with respect to both frames of reference (fixed and movable). One may thus

state

Theorem 5.2.2. In the general motion of a rigid solid, the instantaneous distribution of

the accelerations is the same as in the case of a rigid solid with a fixed point (the pole

of accelerations) at the respective moment.

Kinematics

309

×=



ωω 0 , then the system of linear equations may be impossible, so that points

of null acceleration do not exist (the case of a translation or of a helical motion), or may

be indetermined, existing a straight line (an instantaneous axis of rotation, support of

the vector

) for which all the points have a vanishing acceleration (the case of a

rotation or of a plane-parallel motion). All these particular cases will be considered in

Secs 2.2 and 2.3.

The scalar product of relation (5.2.6) by the vector

, where

′

=a0, leads to a

scalar equation of the form (2.1.53), hence

()0

′

⋅

+×⋅=



ωωωar,

(5.2.8)

where we took into account the relation (2.1.53) and the conditions in which a triple

scalar product vanishes. The solution of this equation is of the form (2.1.53') and we

may write

()

′

⋅

=× × − ×





ωωω

ωω

(5.2.8')

The arbitrary vector

p is determined so that the vector equation obtained from (5.2.6),

where we make

′

, be verified; one observes once more the important rôle played

by the vector product



ωω.

In general,

(,, ) 0×≠



ωωω ω , so that we may represent the vectors r and

′

a in a

frame of reference defined by the three factors of this mixed product, in the form

λμν

++×



ωωωωr ,

OOO

aaa

μν

′′′′

++×



ωωωa

;

(5.2.9)

replacing in the vector equation obtained from (5.2.6), making

′

, and noting that

basis’ vectors are arbitrary, we obtain the scalar system

() 0a

μν

′

⋅+=



ωω ω ,

()0a

ωμ ν

′

−

−⋅ =



ωω

(5.2.9')

λων

′

−

−=

;

We see thus that the determinant of the coefficients of the unknowns is given by the

same formula (5.2.7), similar conclusions being obtained.

The condition (5.2.4) of compatibility of the velocities may be written also in the

form

()

′′

−

⋅=

JJG

;

(5.2.4')

hence, the difference of the projections of the velocities of two points of the rigid solid

on the straight line which links them vanishes (or the difference of the velocities of the

two points is normal to the straight line which links them). Analogously, the condition

(3.2.23'') of compatibility of the accelerations becomes