Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

290

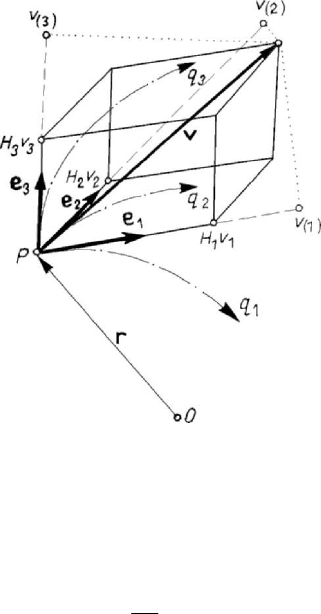
where

 are the components of the velocity (as a matter of fact, they are the

contravariant components, but we do not use this notion, neither the corresponding

notations) in the frame of reference specified by the basis’ vectors

e . The modulus of

the velocity is given by

ij i j

vgqq= ,

(5.1.8')

where we use the formula (A.1.37) of the element of arc.

Taking into account the notations (A.1.40), we may write

iii

∑

vi, vers

ie,

(5.1.9)

Figure 5.2. Velocity of a particle in curvilinear co-ordinates.

being the physical components of the velocity v (Fig.5.2).

Analogously, the orthogonal projections of the velocity

v on the basis’ vectors

e will

be given by

()

v =⋅vi, hence by (without summation for 1, 2, 3i

)

()

∑

(5.1.10)

In the case of orthogonal curvilinear co-ordinates

≠

, so that (without

summation for

1, 2, 3i = )

()

vHv

; (5.1.11)

Kinematics

291

hence, the orthogonal projections of the velocity are the physical components of it. If

the frame of reference is orthonormed, then

123

1HHH

==, obtaining again the

components (5.1.4').

1.1.3 Important particular cases

In spherical co-ordinates, we obtain

vvv

ϕϕ

θθ

++vi i i

, (5.1.12)

where

vr=  , vr

θ=



, sinvr

θϕ

 ,

(5.1.12')

taking into account the results in App., Subsec. 1.1.5; the modulus of the velocity is

given by

2222222

sinvrr rθθϕ=+ +





(5.1.12'')

Analogously, in cylindrical co-ordinates we may write

rr zz

vvv

θθ

++viii, (5.1.13)

where

vr=  , vr

θ=



 ,

(5.1.13')

the modulus of the velocity being given by

22222

vrr zθ





;

(5.1.13'')

in particular, in polar co-ordinates (in the plane

Ox x

), we have

θθ

=+vi i,

 ,

θ=



(5.1.14)

and

2222

vrrθ



(5.1.14')

corresponding to the results in App., Subsec. 1.1.2.

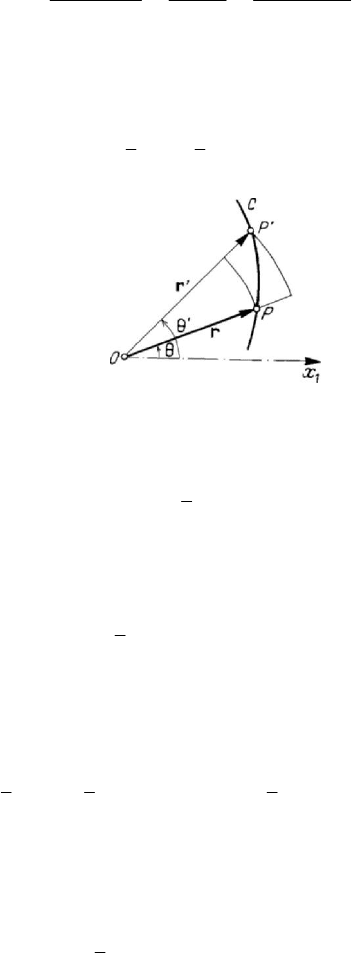
1.1.4 Areal velocity

In the case of a plane trajectory

, we may define a quantity of the nature of a

velocity, which characterizes the variation of the sectorial area between two vector radii

and the arc of the trajectory, when the particle

describes the latter one. Let thus be

the sectorial areas

A and A

′

at the moments

and t

′

, respectively. Noting that

(Fig.5.3)

MECHANICAL SYSTEMS, CLASSICAL MODELS

292

()

tt tt tt

θθ θθ

′′′

′

−−

−

′′ ′

−− −

and passing to the limit for

′

→ , we obtain the areal velocity

AΩ



(in the plane

Ox x ), given by

rrv

Ωθ==



(5.1.15)

Figure 5.3. Areal velocity of a particle.

Vectorially, we have

Ω

=×irvΩ ,

(5.1.15')

where we took into account

ri,

=ii i and the first formula (5.1.14); it

follows also that

()

12 12

xx xxΩ =−

(5.1.15'')

If the trajectory

is a tortuous curve, we may consider formulae of the form

(5.1.15'), (5.1.15'') for the projections of the particle

on the three co-ordinate planes.

We introduce thus the areal velocity

Ω=×=×=



rv rr iΩ

ijk k

xxΩ =∈ 

(5.1.16)

which characterizes the variation of the area of the sector between two vector radii on

the lateral surface of the cone of vertex

O and directrix C .

In particular, if

const==

JJJJG

CΩ , then we may write

() 0

⋅

×=⋅=rrv Cr ;

hence, the trajectory

C is a plane curve, which passes through the origin O of the co-

ordinate axes. In the case of a vanishing areal velocity (

C0), the velocity v has the

same direction as the position vector

r , the trajectory being rectilinear.

Kinematics

293

We notice that one can introduce the torsor of the velocity

v with respect to the pole

O in the form

{}

() ,2

=vv

(5.1.16')

1.2 Acceleration of the particle

We define – in the following – the acceleration of a particle, by introducing the

velocity hodograph; we calculate the acceleration in curvilinear co-ordinates and in

some particular cases of co-ordinates. We introduce accelerations of higher order too,

as well as the acceleration of a discontinuous motion.

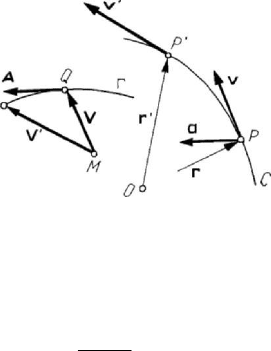
1.2.1 Velocity hodograph. Acceleration

Let M be an arbitrary pole at which we apply the vector V , equipollent to the

velocity vector

v ; if the particle P describes the trajectory C , then the extremity Q

of the vector

V describes a curve Γ , called the velocity hodograph (Fig.5.4).

Observing that

MQ =

JJJG

plays the rôle of a vector radius, it results that the velocity by

which the point

is moving on the curve Γ is the velocity of the velocity of the

particle

P , equipollent to the acceleration a (introduced in Chap. 1, Subsec.1.1.5),

which is invariant with respect to a change of a fixed frame of reference.

Figure 5.4. Hodograph of velocity.

Let

and P

′

be two positions of the particle on the trajectory

. We introduce the

mean acceleration

mean

′

−

′

−

;

(5.1.17)

the instantaneous acceleration (acceleration at the point

) becomes

mean

lim

′

→

aa. (5.1.17')

Taking into account the velocity hodograph, we may write





avr; (5.1.18)

MECHANICAL SYSTEMS, CLASSICAL MODELS

294

the acceleration, applied at the point

P , is thus the derivative of the velocity with

respect to time or the second derivative of the position vector with respect to time.

The components of the acceleration in orthogonal Cartesian co-ordinates are

expressed in the form

iii

avx





, 1, 2, 3i

, (5.1.18')

x being the accelerations of the projections of the point P along the three axes of co-

ordinates. The modulus of the acceleration is given by

ii ii ii

aaa vv xx===



  .

(5.1.18'')

Starting from (4.1.7'), we obtain, by differentiation,

vv vvs

=+=+



a

τττ ,

wherefrom



= , 0a

(5.1.19)

so that

τν

ν , (5.1.19')

taking into account the first formula of Frenet (4.1.10). The component of the

acceleration along the binormal vanishes, hence the acceleration is contained in the

osculating plane. The modulus of the acceleration may be written in the form



(5.1.19'')

We notice that, in the case of a uniform motion (

constv

), the tangential

acceleration vanishes; if

consta

, then the motion is uniformly varied (uniformly

accelerated or uniformly decelerated as

and v have the same sign or are of opposite

signs). The normal acceleration (the acceleration

a too) is directed always towards the

interior of the trajectory (towards the centre of curvature), being centripetal (

≥ );

it vanishes only at the inflection points of the trajectory or in the case of a rectilinear

motion (

1/ 0ρ = ). If the acceleration vanishes (

a0, 0aa

τν

= ), the motion of

the particle is rectilinear and uniform. Starting form the areal velocity (5.1.16), we may

define the areal acceleration in the form

Ω=×=×=





ra rr iΩ ,

ijk k

xxΩ =∈



 ;

(5.1.20)

Kinematics

295

in this case, the torsor of the acceleration with respect to the pole

O is given by

{

}

() () ,2

τ=τ=



ava

(5.1.20')

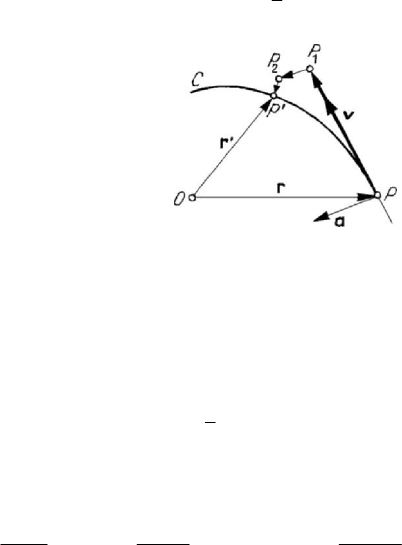
1.2.2 Approximation of the motion of a particle in the neighbourhood of a given

position. Deviation

Let P and P

′

be two positions of a particle, corresponding to the moments t and

′

, respectively. Assuming that the function ()tr is of class

C , we may use the

formula (A.1.20) of Taylor type in the form

( ) () ( )() ( ) () (, )

ttttttttttt

′′ ′ ′

=+− +− + −



rr r rη ,

Figure 5.5. Deviation of a particle.

where

(, )tt t

′

−η represents the rest. We can thus approximate the motion of the

particle

P in the neighbourhood of the point P by

1122

PP PP P P P P

′

=+ +

JJJG JJJJG

JJG JJJJG

(Fig.5.5), with

()()PP t t t

′

=−

JJG



r ,

()()

PP t t t

′

=−

JJJG



r ,

(, )PP t t t

′′

−

JJJG

;

(5.1.21)

for a fixed

t , we may write

()

′

JJG



()()

ttt

′

=−

′

JJJG



()

′

JJJG



(5.1.21')

We can thus state

Theorem 5.1.1. The continuous motion of a particle P may be approximated, at a

given moment

t , in a neighbourhood of first order (the segment PP

′

JJJG

), by a rectilinear

and uniform motion along the tangent at

P to the trajectory, where the velocity is

equal to the velocity of the particle at

P . As well, in a neighbourhood of second order

(the segments

JJG

and

JJJG

), the motion can be approximated by a succession of two

rectilinear motions: the motion previously presented, to which a uniform varied motion

with the acceleration of the particle at

P is added.

MECHANICAL SYSTEMS, CLASSICAL MODELS

296

The time interval

′

− is very small in a vicinity of first order; in a vicinity of

second order, this interval is somewhat greater, but still small, so that the segment

′

JJJG

η is negligible. The vector

JJJG

is called deviation; its rôle is to bring back

the particle

P from the tangent (on which it moves if it is not acted by a force,

according to the principle of inertia) on the trajectory

C .

1.2.3 Acceleration of a particle in curvilinear co-ordinates

Starting from the expression (5.1.8) of the velocity, by differentiation, one obtains

jjjj

kjkk

qq q qq q

qq q

∂∂

=+=+

∂∂ ∂

     

aee

(5.1.22)

Noting that

kk kkj

aag⋅= ⋅=ae e e ,

ij i

kj k

gg δ

we may write

[]

il il il il

ijjjij

lljk k l k

ag gqq gqq jklgqq=⋅=⋅ +⋅ =+     ae e e e e ,

using the notations introduced in App., Subsec.1.1.5, where

[

]

,jk l is Christoffel’s

symbol of first species. With the aid of Christoffel’s symbol of second species (A.1.45),

we may write the components (contravariant components) of the acceleration in the

frame

e in the form

ii j

aq qq

⎧⎫

⎪⎪

⎨⎬

⎪⎪

⎩⎭

   , 1, 2, 3i

(5.1.22')

The physical components of the acceleration are

, while the

orthogonal projections of the acceleration on the basis’ vectors

e are written in the

form (without summation with respect to

1, 2, 3i

)

()

∑

(5.1.23)

In the case of orthogonal curvilinear co-ordinates, we have (without summation with

respect to

1, 2, 3i = )

()

aHa

, (5.1.23')

so that the orthogonal projections of the acceleration are its physical components. For

an orthonormed frame of reference (

123

1HHH

==) we find again the

components (5.1.18').

Kinematics

297

Using a method due to Lagrange, we can calculate the components of the

acceleration also in a movable system of curvilinear co-ordinates, given by

(

)

123

,,;qqqt

rr .

(5.1.24)

We have

jjj

∂

+= +

∂∂





ver

wherefrom

∂

∂∂



;

then

dd d

ii i

tq t q tq

∂∂ ∂

⎛⎞ ⎛⎞

⋅= ⋅ = ⋅ −⋅

⎜⎟ ⎜⎟

∂∂ ∂

⎝⎠ ⎝⎠

vr r r

ae v v

We notice that

iji i

tq qq tq

∂∂ ∂

⎛⎞

⎜⎟

∂∂∂ ∂∂

⎝⎠



rr r

iij i

qqq qt

∂∂ ∂

∂

∂∂ ∂∂



vr r

;

because the vector function

r is of class

C , it follows

(

)

iii

tq q q t

∂∂∂

⎛⎞

⎜⎟

∂∂∂

⎝⎠

rv r

so that the operators

d/dt and /

∂

∂ are permutable. Finally, we get (covariant

components of the acceleration)

d1d1

d2d2

ii ii

tq q tq q

∂

∂∂∂

⎛⎞

⋅= ⋅ −⋅ = −

⎜⎟

∂

∂∂∂

⎝⎠

ae v v

wherefrom

tq q

∂∂

⎡⎛ ⎞ ⎤

=−

⎜⎟

⎢⎥

∂∂

⎣⎝ ⎠ ⎦



, 1, 2, 3i

(5.1.25)

obtaining thus Lagrange’s formula.

MECHANICAL SYSTEMS, CLASSICAL MODELS

298

1.2.4 Important particular cases

Taking into account the results in App., Subsec. 1.1.5, we obtain, in spherical co-

ordinates,

aaa

ϕϕ

θθ

++ai i i, (5.1.26)

with

222

sin

arr rθθϕ=− −



 

()

22 2

2 sin cos sin 2

ar rr r

θθ θθϕ θ θϕ=+ − = −

  

 

()

sin 2 sin 2 cos sin

sin d

arrr r

θϕ θϕ θθϕ θϕ

=+ + =



    

(5.1.26')

Analogously, in cylindrical co-ordinates, we get

rr zz

aaa

θθ

++aiii

, (5.1.27)

where

arrθ=−





2ar r

θθ=+

 



 .

(5.1.27')

In particular, in polar co-ordinates, in the plane

Ox x , we may write

θθ

=+ai i,

arrθ=−





()

ar r r

θθ θ=+ =

  



(5.1.28)

1.2.5 Accelerations of higher order

As we have seen in Chap. 1, Subsec. 1.1.4, the derivatives of higher order of the

position vector are invariant with respect to changes of a fixed frame of reference; these

derivatives are identified with the derivatives of the acceleration

, which will be

called acceleration of first order (

()

aa). We obtain thus accelerations of higher

order: the acceleration of second order (

()



aar), the acceleration of third order

(

()



 

aar) and – in general – the acceleration of nth order, given by

()

−+

−

(5.1.29)

Although the accelerations of higher order do not intervene directly in the Newtonian

model of mechanics, which needs only the acceleration of first order, one considers that

some mechanical phenomena (collisions, seismic phenomena, etc., which take place by

a rapid variation of the intensity of the force) may lead to other mathematical

modelling, in which these accelerations play an important rôle.

Kinematics

299

Starting from formulae (5.1.19), (5.1.19'), which give the acceleration of first order

with the aid of its intrinsic components (along Frenet’s trihedron axes), and using

Frenet’s formulae (4.1.10), (4.1.10'), we get

()

() () ()

22 2

aaa

τν

=++

(5.1.30)

where

()

=−



()

=−



()

ρρ

=−

′

(5.1.30')

We notice that the acceleration of second order has a component along the binormal

too, which vanishes only in the case of a rectilinear trajectory or, more general, of a

torsionless trajectory (in the osculatory plane). The acceleration of second order along

the principal normal vanishes (for a curvilinear trajectory) if

= ,

(5.1.31)

where

ρ and

v correspond to the moment

(for instance, in the case of a

uniform circular motion).

Obviously, the acceleration of second order may be introduced also with the aid of

the hodograph of the acceleration of first order.

1.2.6 Acceleration in case of a discontinuous motion

In the case in which the position vector is a continuous function on

[

]

,tt

′′′

, while

the velocity and the acceleration are continuous on the same interval, excepting a finite

number of moments

[

]

ttt

′

′′

∈

, 1,2,...,in

(piecewise continuous), to which

correspond discontinuities of the first species, that is

(

)

(

)

tt−≠ +vv,

(

)

(

)

−

≠+aa,

(5.1.32)

it is necessary to use methods of the theory of distributions. The integrals

()d

′′

′

∫

v , ()d

′′

′

∫

(5.1.33)

do exist in these conditions.

Taking into account the formula (1.1.51), we may write

()

d() d()

=+δ−

∑



(5.1.34)