Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

270

36nb

+ , (4.2.51)

where

b is the number of bars, while n is the number of nodes; this is a necessary

condition of non-deformability of the articulated system.

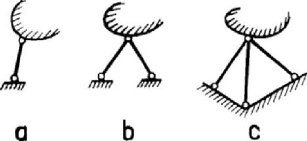
If the articulated system is not free, then it is necessary to introduce constraints

equivalent to six simple supports, which may be materialized by pendulums; besides

simple supports (which allow the rotation in any direction and the displacement in a

plane normal to its direction, Fig.4.44,a), such constraints may be plane hinges (double

supports, materialized by two concurrent pendulums, which allow the rotation in any

direction and a displacement along a direction normal to the plane of the support,

Fig.4.44,b) and spherical hinges (triple supports which allow the rotation in any

direction, but not one displacement is allowed, Fig.4.44,c).

Figure 4.44. Simple (a), double (plane hinge) (b) and triple (spherical hinge) (c) supports.

The relation (4.2.51) becomes a more general form

3nbs

6s ≥

, (4.2.51')

where

s is the number of simple supports.

With the three types of supports mentioned above one can obtain various supporting

systems; for instance, a simple support, a double support and a triple support ensure the

fixity in space of the articulated system. In general, the six pendulums (the six bars) of

the supporting system must fulfil some conditions to ensure a correct fixity of the

articulated system, hence to avoid a critical case. These critical forms may be identified

– in general – on a static way (by equations of projection and of moment) or on a

kinematic way (analysing all the possibilities of motion). Thus, not one straight line

about which the resultant moment of all the constraint forces be zero must exist,

because the resultant moment of all the given forces about this line (which – in general

– does not vanish) could no more be equilibrated; in this case, the articulated system

could rotate about this straight line. As well, there must not exist some straight line so

that the sum of the projections along it of all the six constraint forces be zero, because

the projection along the very same line of the resultant of the given forces would no

more be equilibrated; in this case, the rigid solid would have a motion of translation.

We mention also that a certain number of pendulums of the six ones must not constitute

a plane critical form (for instance, three coplanar pendulums do not be concurrent).

Among the critical forms which are the most encountered, depending on the

directions of the supports’ pendulums, one can mention the following ones: the case in

which all the six directions pierce the same straight line; the case in which two sets of

three directions are parallel or concurrent; the case in which at least four directions are

parallel or concurrent or are coplanar; the case in which two directions are in a plane

Statics

271

which contains also the piercing point of other three directions; the case in which three

directions are coplanar, the plane containing also the piercing point of other two

directions; the case in which five directions are in two planes, their intersection of

which is coplanar with the sixth direction; the case in which all the six directions are in

parallel planes. These results may be easily verified. We consider that a thorough

examination of the supporting system is very important, to can avoid the critical cases.

If the supporting is correct, then the six unknown reactions may be determined by a

system of six scalar equations with six unknowns; in some particular case, one can

make various observations, simplifying thus the computation. The condition (4.2.51') is

only a necessary condition of geometric non-deformability; besides this condition, one

must verify if the articulated system is not a critical form. In this case, to very small

variations of the lengths of the bars correspond very great displacements of the nodes;

expressing the conditions of equilibrium on the deformed form of the articulated

system, to an arbitrary loading may correspond very great values of the efforts in bars

or some particular load may lead to indeterminate efforts.

The efforts in the members of the articulated system are given by a system of

equations with

3n unknowns (the equations of equilibrium in each node), so that the

condition of non-deformability of such a system is given by

≠ , (4.2.52)

where

Δ is the determinant of the coefficients of the system of equations.

Because it is rather difficult to express such conditions for a great

n , in particular

cases one may use some special methods of investigation. Thus, if no one force is

applied at the nodes (hence, if one applies null loads), then all the free terms of the

system of equations vanish and, if we take into account the condition (4.2.52), the

system has only zero solutions. Hence, in the method of null loading, if one succeeds to

show that, for zero loads at the nodes, all the efforts in the bars vanish, then it follows

that the articulated system is not a critical form; otherwise, this system is a critical form.

On the other hand, the relation (4.2.51') ensures us that the articulated system is

statically determinate; if

3bs n

< , then the system is a mechanism, while if

3bs n+> , then the system is statically indeterminate. If we have 6s = in the

relation (4.2.51'), then the system is a free articulated system, the geometric non-

deformability of which does not depend on the constraints.

Besides the simple articulated systems, we mention also the compound articulated

systems, obtained by the composition of various simple systems with the aid of some

bars of connection. The complex articulated systems are those which cannot be reduced

to simple articulated ones.

An important case is that of articulated spatial systems which form a polyhedron

without internal diagonals. One may thus use polyhedra the faces of which are

constituted by plane trusses, their nodes being on the edges of the polyhedra. We notice

that the conditions of geometric non-deformability are fulfilled. To prove this assertion,

we start from Euler’s relation

2mn f

−

=−, (4.2.53)

MECHANICAL SYSTEMS, CLASSICAL MODELS

272

valid for a closed polyhedron, where

n is the number of vertices, m is the number of

edges and

is the number of faces. Assuming that each face is a triangle, each edge

being common to two faces, and each face having three edges, we find the

supplementary relation

23mf

; (4.2.54)

eliminating

between the last two relations, we may write

36mn

−

. (4.2.53')

Noting that the edges are just the bars of the truss (

), it follows that the relation

(4.2.53') is equivalent to the relation (4.2.51); the non-deformability of this articulated

system is thus emphasized. If each face of the polyhedron is constituted by a plane

truss, non-deformable from a geometric point of view, having nodes only on the edges,

so that at each node be at least three coplanar bars, then the above reasoning is valid;

such a spatial framework is geometrically non-deformable.

We notice that the hypothesis of perfect hinges at the nodes has a greater importance

in the spatial case than in the plane one. Indeed, in this case, the rigidity of the nodes

may have a great influence on the values of the efforts in bars.

To state the efforts in bars, we use – in general – the same methods of computation

as in the plane case. We mention thus the method of isolation of nodes, which can be

applied analytically, as well as graphically; one must have at the most three unknown

efforts (the reactions are obtained – previously – from conditions of global equilibrium)

at each node. In the method of sections, each section must cut at the most six bars with

unknown efforts. Eventually, one can combine the two methods. These methods are no

more sufficient – in general – in the case of complex structures; then one must use the

method of bars replacing of Henneberg or the two sections method of Tsaplin. If it is

possible, then one can make also a decomposition of the spatial articulated system in

several plane articulated systems, which are separately studied.

2.1.9 Open articulated systems

We call open articulated system (polygonal articulated line, chain) a system of

articulated bars having the form of a polygonal line; if such a system is constituted of

more than two bars, then it is movable. Assuming that the system of given and

constraint external forces

, , ,...,

FFF F, equivalent to zero, is acting at the nodes

, , ,...,

PPP P (Fig.4.45,a), one must find the form of the polygonal line, as well as

the efforts

01 10

=−NN,

12 21

−NN,…,

1, , 1nn nn

−

−NN in the bars (according to

the considerations synthetized in Fig.4.41, we assume that these forces are applied at

the respective nodes). An open articulated system is called simply connected because,

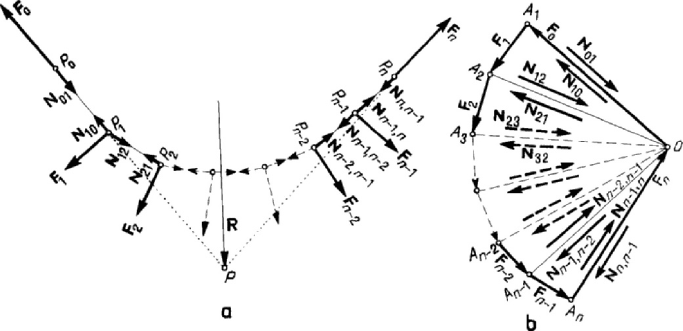
Statics

273

considered in the previous subsection, which are called multiply connected (they are not

losing their unity by suppressing an intermediary bar).

For the equilibrium of an open articulated system, it is necessary and sufficient

that each node of it be in equilibrium under the action of the external loads (given

and constraints), as well as of the internal ones (efforts in bars). To the node

corresponds the polygon of forces

OA A , to the node

P the polygon of forces

OA A a.s.o., while to the node

−

the polygon of forces

OA A

−

; we construct

these polygons in a cumulative polygon of forces

...

OA A A , where the internal

forces corresponding to two consecutive nodes equilibrate one the other (Fig.4.45,b).

The polygons corresponding to the nodes

P and

P are reduced to segments of

straight lines. The point

O is called pole,

, ,...,

OA OA OA being polar radii. The

geometric figure formed by the sides of the articulated polygonal line, parallel to the

polar radii, is called funicular (link) polygon. Firstly, one constructs the polygon of

forces

...

OA A A (the forces

F and

F may be external constraint forces); the

funicular polygon sides are then drawn, by parallels to the polar radii (the length of

which is proportional to the magnitude of the efforts in bars, at a certain scale, the

directions of these efforts being so as to close the polygons of forces). Thus, the

position of equilibrium of the open articulated system, as well as the constraint forces

and the efforts in bars are specified.

Figure 4.45. Funicular polygon (a). Polygon of forces (b).

Because the external force which acts at a node forms a triangle with the efforts in

the contiguous bars, there results that this force and the two adjacent bars are coplanar;

thus, an open articulated system acted upon by coplanar external forces is contained in

the respective plane too. If in all the bars arise efforts of tension, then the polygonal

articulated system may be replaced by a perfect flexible and inextensible thread, acted

upon analogously, obtaining the same results.

by suppressing an intermediary bar, it loses its unity, unlike the closed systems,

MECHANICAL SYSTEMS, CLASSICAL MODELS

274

The graphic construction of the polygon of forces and of the funicular polygon is

particularly useful in many plane problems. Thus, the resultant

R of the external forces

12 1

, ,...,

n −

FF F is specified in direction and magnitude by the oriented segment





;

one can show that the resultant passes through the piercing point

P of the extreme

sides of the funicular polygon (Fig.4.45,a). If the polygon of forces is closing, then two

cases may take place: if the two sides of the funicular polygon are parallel, then the

system of forces is reduced to a couple, while if these sides coincide, then the system of

forces is equivalent to zero. We may state

Theorem 4.2.5. The necessary and sufficient condition of equilibrium of a system of

coplanar forces which act upon a rigid solid (forces modelled by sliding forces)

consists in the closing of the polygon of forces, as well as of the funicular polygon.

Let be

n coplanar forces

, ,...,

FF F

. One can show that the

1n +

sides of a

funicular polygon, corresponding to a pole

, pierce the corresponding sides of

another funicular polygon, corresponding to a pole

, in

points on a straight

line parallel to

; this one is called the Culmann straight line. Starting from this

property, one can easily see that, for a system of given forces, all the funicular polygons

which pass through two fixed points

and

P have their poles on a straight line

parallel to

. Finally, one proves that there is only one funicular polygon which

passes through three non-collinear given points. These basic properties allow the

graphical study of a system of forces which act upon a rigid solid or upon a system of

rigid solids and constitute the basis of the methods of graphical statics. For instance,

one can decompose a force along three non-concurrent coplanar supports, one can

construct the moment of a system of forces, one can determine reactions in a graphical

way, one can calculate graphically (with a certain approximation) static moments

(obtaining thus the position of centres of gravity), moments of inertia etc.

Figure 4.46. Polygonal articulated line. Analytical method.

Analytical methods imply – in general – a great volume of computation. Let us

consider the particular case of an open articulated system, the extremities of which are

fixed at two fixed points, and which is acted upon by equidistant equal parallel forces;

such a system may be encountered in the case of suspension bridges. We consider thus

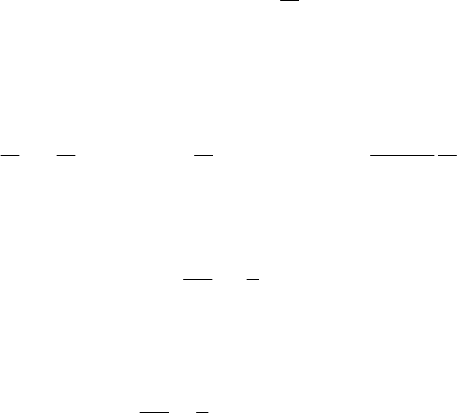
Statics

275

the articulated polygonal line

...

PPP P , acted upon by the forces

12 1

...

n −

=== =FF F F with respect to a Cartesian right-handed frame of reference

Oxy

. We use the notations in Fig.4.46, assuming – for the sake of simplicity – that

OP≡ . We may thus write

,1 1, ,1 ,1

cos cos const

ii i i ii ii

NNHαα

−− + +

== ,

,1 1, ,1 ,1

sin sin

ii i i ii ii

NFNαα

−− + +

= ,

where

1, , 1ii ii

−

= is the modulus of the effort in the bar

−

, while

is the

constant modulus of the projection of this effort on the

Ox - axis; eliminating the efforts

in bars, we get

1, 01

tan tan ( 1)

αα

−

=+−.

The ordinate of the point

will be

(

)

01 12 1,

tan tan ... tan

ya αα α

−

=+++

01 01

(2)

tan 2 ... ( 1) tan

FF F F

ai i ai

HH H H

αα

−

⎡

⎤

⎡⎤

=++++−=+

⎢

⎥

⎢⎥

⎣⎦

⎣

⎦

;

noting that

xia=

, we have

(

)

tan 1

ii i

yx x

+−.

Hence, the open articulated system considered above can be inscribed in a parabola of

equation

(

)

tan 1

yx x

α=+−.

(4.2.55)

Knowing the co-ordinates of the point

P , one can determine the angle

α , as well as

the modulus

H .

2.2 Statics of threads

As we have seen in Chap. 1, Subsec. 1.1.10, a thread is a deformable solid (a bar) for

which two dimensions (of the cross section) are completely negligible with respect to

the third dimension (the length); one considers that the threads are perfect flexible and

torsionable (they cannot take over efforts of bending and of torsion), even if – in reality

– such ideal models do not exist, as it was shown in Subsec. 2.1.6 (Fig.4.28). We

suppose also that the threads to study (materialized by cables, chains, ropes etc.) are

inextensible. In reality, such threads do not exist; to take into consideration their

extensibility (as in the case of rope bridges) passes beyond the frame of this chapter.

MECHANICAL SYSTEMS, CLASSICAL MODELS

276

After deducing the equation of equilibrium of threads, together with a study of them,

we will consider some particular cases of equilibrium under the action of distributed or

concentrated loads; as well, we will emphasize the problems which arise in the case of

threads constrained to stay on a surface.

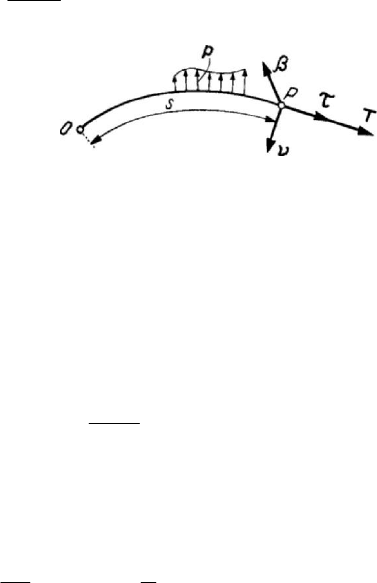
2.2.1 Equilibrium equations of threads

Because its thickness is negligible, a thread may be modelled by its axis, the points

of application, both of the external forces and of the efforts being thus situated on this

axis. If in the equations of equilibrium of a bar (4.2.36) we neglect the moments on the

cross section as well as the moment external loads (because of the perfect flexibility and

torsionability), we may express the equilibrium of threads in the form

d()

()

, () ()ss

=R0

(4.2.56)

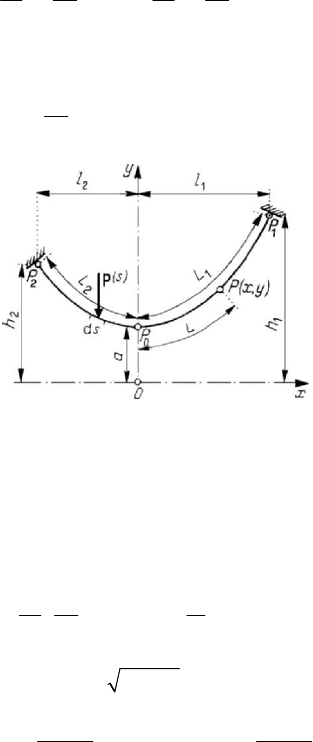
Figure 4.47. Equilibrium of a thread.

where

()sp is the external load (considered distributed on the unit length of the

thread), applied at the point of curvilinear abscissa

s , while ()sR is the resultant of

the efforts on the corresponding cross section. Taking into account the model assumed

for the thread, as well as the second equation (4.2.56),

()sR is reduced to the axial

force of tension

()sT (one uses the letter T , from the word tension), along the unit

vector τ , tangent to the thread (Fig.4.47); the equation of equilibrium is thus reduced to

d()

()

p0.

(4.2.57)

Noting that the effort

() ()()sTss

, where () 0Ts ≥ is the tension in the thread,

at the section

s , we may write the equations of equilibrium with respect to Frenet’s

trihedron in the form

+=, 0

= , 0p

(4.2.57')

where we took into account Frenet’s formula (4.1.10). Extending the considerations

made in the previous subsection concerning articulated polygonal lines and passing to

the limit, one obtains the threads; hence, their form of equilibrium is a funicular curve.

The third equation (4.2.57') shows that, for equilibrium, the external load

p must be

contained in the corresponding osculating plane, in any point of the funicular curve. It

results that, in the case of external coplanar loads, the funicular curve is a plane one; the

Statics

277

same conclusion is obtained if the load

p is of constant direction ( ()ps=pu,

const=





u ). Finally, if the distributed load p has the same support, the funicular curve

becomes a straight line, which coincides with the common support; this happens also if

the thread is not acted upon by some forces (

) or is acted upon only by tangential

forces (

= ). The first two equations (4.2.57') show that the external load p is

directed towards the convex part of the funicular curve (because

/0pT

ρ=− < ),

exactly in the direction of the decreasing tensions (

d/d 0pTs

−>, for

decreasing). Moreover, the tangential component

of the external load specifies the

tension

T ; then, the normal component p

determines the curvature 1/ρ , hence the

funicular curve. If the external load

p is normal to the thread for any s (hence if

= ), then the tension T is constant; one can thus explain why the tension T

remains constant along a thread, even if this one passes frictionless over a pulley. This

observation remains valid also in the case of a thread of negligible weight, on a smooth

surface (

constT

), if the funicular curve is a geodesic line of the surface ( ν is along

the normal to the surface).

An interesting particular case is that in which the external force is conservative,

deriving from a potential

()UUs

, hence the case in which

gradU

p ,

= .

(4.2.58)

The first equation (4.2.57') leads to

constTU

= ; (4.2.58')

by choosing in a convenient form the origin

O , the constant can be taken equal to zero,

the tension in the thread being thus specified. We notice that the tension

T is constant

at all the points of a thread on an equipotential surface.

Referring the equation (4.2.57) to the orthonormed frame

Ox ,

1, 2, 3i

, we get

(

)

= , 1, 2, 3i

;

(4.2.59)

associating the relation

(4.2.59')

too, we can determine the unknowns

()Ts and ()

xs, 1, 2, 3i

. The four differential

equations (4.2.59), (4.2.59') are of first order with respect to

T and of second order

with respect to the co-ordinates; the six constants of integration thus introduced are

determined by boundary conditions (for instance, bilocal conditions at the two

extremities of the thread).

MECHANICAL SYSTEMS, CLASSICAL MODELS

278

2.2.2 Particular configurations of equilibrium

Let be a thread fixed at the points

P and

P , acted upon by a distributed load ()sp

of constant direction, proportional to the element of arc (for instance, the own weight).

According to an observation in the previous subsection, the funicular curve will be a

plane one. Referring to a right-handed orthogonal Cartesian system

Oxy , we may write

(

)

(

)

wherefrom

const

(4.2.60)

Figure 4.48. Catenary curve.

the tension at the point

being thus constant and equal to

(Fig.4.48). This result

has a more general character; if the external load is of the form

()ps

pu, const=





u ,

then the projection of the tension on a direction normal to the unit vector

u is constant.

Eliminating the tension

, we get

(

)

(4.2.61)

wherefrom, taking into account

d1dsyx

′

=+ and integrating, we obtain

sinh

−

′

cosh

yy a

−

−=

;

hence, the funicular curve, called catenary curve in this case, is a hyperbolic line.

Effecting a translation of the co-ordinate axes towards the position in Fig.4.48, we find,

finally (without losing anything of the generality)

Statics

279

cosh

, sinh

′

, cosh

TH py

;

(4.2.62)

the last relation corresponds to the formula (4.2.58'), the considered external force

being conservative (

grad( const)py=−+p ). We notice that the length of the arc of

curve between the points

P and P is given by

dsinh

Lsa

∫

222

Lya

− ,

(4.2.62')

and the curvature at a current point is expressed in the form

1 a

= .

(4.2.62'')

Taking into account the position of the points of suspension

P and

P (Fig.4.48), we

introduce the notations

2ll l

+ ,

2hh h

− ; the total length of the catenary

curve

LL L=+ and the difference of level 2h are given by

2 sinh sinh

⎛⎞

⎜⎟

⎝⎠

2 cosh cosh

⎛⎞

=−

⎜⎟

⎝⎠

so that

22 2 2

sinh

Lh a

−=

(4.2.62''')

Noting that

() ()

sinh

1 ...

3! 5!

Lh l l

laa

−

=+ + +

and taking into account that the function in the second member is increasing for

/(0,)la∈∞, it results that this equation has only one positive root a , function of the

known parameters

and

; the condition

22 2

lh L

< must be fulfilled, hence

the length of the thread must be greater than the distance

If such a thread has a large span and a very small deflection with respect to it, then

the tension is increasing very much. In this case, the projection

H of the tension is

greater than the own weight of the thread; one can thus neglect the powers greater than

3 of the ratio

2/pL H and – obviously – of the ratio //px H x a

. Hence,

sinh

xxx

≅+

cosh 1

≅+