Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

250

∑

2(sin cos )

PfNαα,

=−

∑

(cos sin )

QfNαα,

where

is the normal reaction at the point

P of the lateral surface, P is the force by

which the wedge is beaten,

Q (

⊥

QP) is the force by which the wedge pushes

laterally each piece, while

tan

is the coefficient of sliding friction. Noting that

FP, =

FQ, there results

sin cos

22tan()

cos sin

mrr

FFF

αα

αϕ

αα

==+

−

(4.2.15)

Figure 4.23. The equilibrium of a wedge.

We observe that one obtains a great pressure

Q with the aid of a small force

, if α

and

ϕ are small angles. If the wedge is pulled out, then the direction of the friction

force is changing and one obtains the relation

2tan( )

FFαϕ

− .

(4.2.15')

≤

F , hence if ≤αϕ, then the wedge remains self-fixed.

The asymmetric wedge with a simple or a double inclination can be studied

analogously.

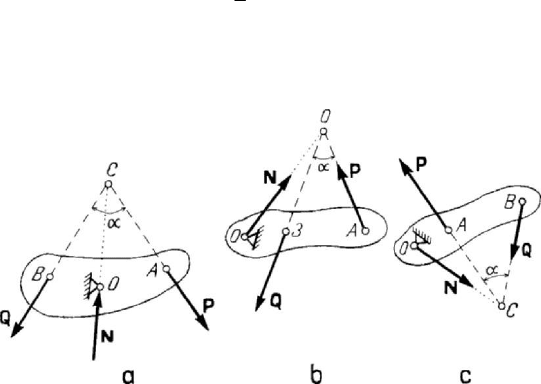
The screw is a simple device used for detachable installings with clamping, for the

transmission of motion (by transforming the motion of rotation in a motion of

translation and inversely), for the adjustement of the relative position of two pieces or

for the elimination of wear plays, as well as for the measuring of the lengths. On the

lateral surface of a right circular cylinder is cut a screw thread in the form of a circular

helix; developing the lateral surface of the cylinder, it is easy to verify that the slope of

the helix is given by the relation

tan

= ,

(4.2.16)

Statics

251

where

p is the pitch of the helix, while r is the radius of the cylinder. The screw is

thread in the nut, its relative motion with respect to it being a particular helical motion,

called a screw motion. It is possible that the nut be fixed, the screw having a helical

motion or the screw be fixed and the nut having such a motion or the nut have a motion

Figure 4.24. The equilibrium of a screw.

of rotation and the screw a motion of translation or – finally – the screw have a motion

of rotation and the nut a motion of translation. In the first of these cases, at one of the

extremities acts upon the screw a turning (motive) couple of moment

MPl= , where

FP is the intensity of the force which acts at the end of a lever arm of length l ; at

the other extremity is acting a resistent force

FQ along the screw axis, with a

direction opposite to that of the screw driving. In any point

of contact with the nut

fillet arises a force representing its action of component of modulus

, normal to the

fillet, and of component of modulus

TfN

, tangent to this one, guided in a direction

opposite to the direction of displacement of the screw fillet with respect to that of the

nut (Fig.4.24).

The equations of equilibrium (projection on the screw axis and moment about the

same axis) lead to

=−

∑

(cos sin )

QfNαα, =+

∑

(sin cos )

Mr f Nαα,

wherefrom

sin cos

tan( )

cos sin

MQr Qr

αα

αϕ

αα

==+

−

(4.2.17)

where

tan

ϕ is the coefficient of sliding friction. By unscrewing, the direction of

the friction forces is changing, so that one must have

MECHANICAL SYSTEMS, CLASSICAL MODELS

252

tan( ) tan( )

Qr M Qrαϕ αϕ

−

≤≤ +

(4.2.17')

for equilibrium. We notice that for

= /2αϕ π the turning moment

M (hence, the

motive force

F ) must be sufficiently great to can obtain the clamping of the screw; it

is the case of self-locking. As well, for

αϕ it is necessary to act with a turning

moment

of a direction opposite to that of the clamping for screwing, independent

of the force

Q ; in this case, the screw is self-fixed.

The level is a simple device formed by a rigid solid with a fixed point or axis, acted

upon by two forces: a motive force of intensity

FP and a resistent force of

intensity

FQ. The supports of these forces are contained in a plane normal to the

axis of rotation of the rigid solid and do not pierce this axis.

Neglecting the frictions, the equation of moments with respect to the fixed point or

axis leads to Archimedes’ relation

(4.2.18)

where

a is the level arm of the motive force, while b is the level arm of the resistent

force.

Figure 4.25. The level of first (a), second (b) or third (c) order.

As a function of the position of the articulation

O with respect to the points of

application

A and B of the motive and resistent force, respectively, the levels may be

of three kinds. At the level of first order, the hinge

O is between the points A and B

(Fig.4.25,a); if

=ab, then it results

FF (the case of the balance with equal

arms), if

>ab, then it results

FF (case in which motive force is saved), and if

<ab, then one obtains >

FF (non-economic case). The levels of second order are

those for which the point

of application of the resistent force is between the points

and A (Fig.4.25,b); in this case,

>ab

, hence

FF (motive force is saved). In

the case of the levels of third order the point

A of application of the motive force is

between the points

O and B (Fig.4.25,c); in this case

ab, hence >

FF (non-

economic case).

Statics

253

Taking into account the friction in the bearing, we may use the formula (4.2.8),

obtaining the equation of equilibrium

′

−

=Pa Qb f Nr ,

(4.2.19)

where

r is the hinge journal radius,

′

is the corresponding coefficient of friction,

while

N is the modulus of the reaction, given by

=++

2cosNPQPQα ,

(4.2.19')

α being the angle formed by the forces P and Q . There result the extreme values of

the motive force

F (for equilibrium)

()

′′ ′

=+±++−

′

−

22 2 2 22 2

222

cos 2 cos sin

Fabfrfrababfr

afr

ααα.

(4.2.20)

In the particular case

= 0α ( PQ ), we get

FkF

;

(4.2.21)

the ratio

/ba in the formula (4.2.18) is thus multiplied by the coefficient

′

−

(4.2.21')

Hence, a motive force greater than that used if there are not frictions is necessary.

To obtain scale ratios greater than

/ab (corresponding to a single level), one may

use systems of articulated levels.

The level is the basic element for weighting apparatuses. We mention thus the

balance with equal arms, the Roman balance, the decimal balance, the Roberval

balance etc.

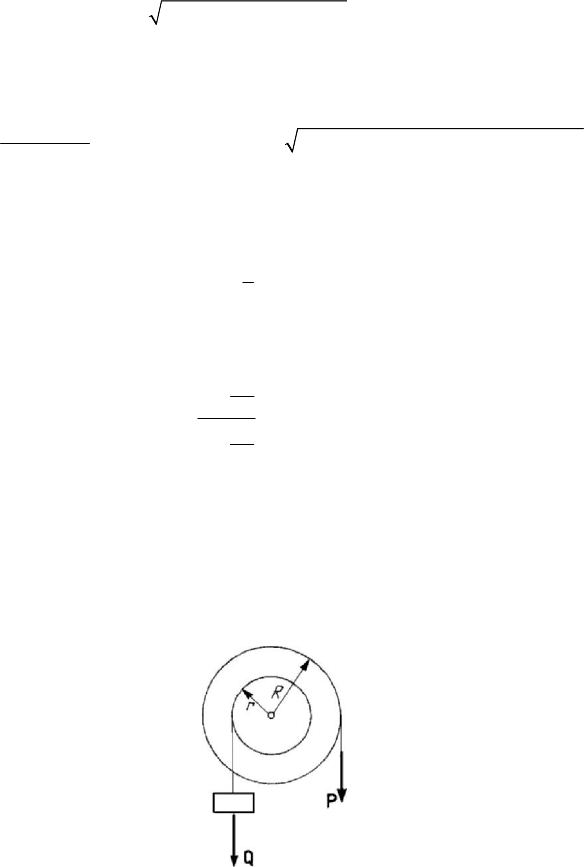
Figure 4.26. Equilibrium of a cable hoist.

MECHANICAL SYSTEMS, CLASSICAL MODELS

254

The cable hoist is a simple device used to raise the weights. The simple hoist is

formed by a cylindrical drum of radius

r , on which a cable is rapped up; an extremity

of the cable is fixed to the drum, while by the other extremity the weight (the resistent

force)

, which must be raised, is hanging down. On the drum is fixed a wheel

of radius

R , on which the motive force

is tangentially applied (Fig.4.26). The

equation of moment with respect to the rotation axis leads to

(4.2.22)

To maintain

= const

F when taking into account the own weight of the cable too,

one may use a truncated cone drum (regulator cable hoist). Sometimes, a hoist with a

vertical axis is called a capstan. In the case of a differential hoist, the drum is

constituted of two cylindrical sections of different radii, on which a cable is rapped up,

in distinct directions, raising a weight

Q with the aid of a pulley.

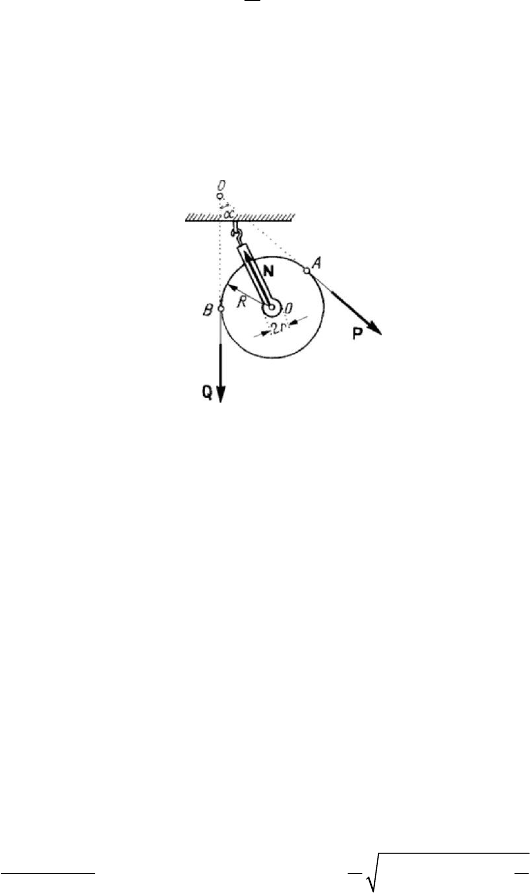
Figure 4.27. Equilibrium of a pulley.

The pulley is a simple device constituted of a circular disk of radius

R , on the

circumference of which passes a cable (chain); the axle of the pulley is fastened by a

fork with a hook. The fixed pulley has a fixed axle, while the movable pulley has a

shifting one.

At the two extremities of the cable of a fixed pulley (Fig.4.27), the forces

=FP

and

=FQ

are acting so that, in the absence of frictions, we have

FF. (4.2.23)

Taking into account the friction in the bearing, we may write

′

−

=()PQR fNr,

(4.2.24)

where

r is the radius of the pulley journal,

′

is the coefficient of friction of the

bearing, while

N is the modulus of the reaction, given by a formula of the form

(4.2.19'). We get

(

)

′′′

=+±−

′

−

2222 2222

222

cos 2 cos sin

FRfrfrRfr

Rfr

αα

. (4.2.25)

Statics

255

In the particular case

= 0α ( PQ ), there results

+NPQ

, and we may write

FkF, (4.2.26)

the multiplicative coefficient

k being given by

′

−

(4.2.26')

Figure 4.28. Influence of the rigidity of the cable in the equilibrium of a pulley.

In general, the cable is supposed to be perfectly flexible; in reality, the cable has a

certain rigidity, so that in the zones

′

AA and

′

BB it nears by

e the pulley axle or

moves to a distance

e from this one, the curvature having a continuous variation

(Fig.4.28). The equation of moments yields a relation of the form (4.2.26) too, where

′

−−

ee fr

Re fr

;

(4.2.26'')

neglecting

e with respect to R , we can also write

′

=++

′

−

Rfr

λ ,

(4.2.27)

where the influence of the rigidity is given by

′

−

Rfr

λ .

(4.2.27')

Because

> 1k , we have >

FF, and the simple fixed pulley has now the rôle to

change the direction of transmission of the force (in fact, its support).

The movable pulley allows to raise a weight

Q using a force P of a smaller

intensity (

FF). For instance, in the case of the movable pulley for which PQ

(Fig.4.29) we have

MECHANICAL SYSTEMS, CLASSICAL MODELS

256

FF,

(4.2.28)

Figure 4.29. Equilibrium of a movable pulley.

the tension in the cable being

/2TP . If we take into account the frictions and the

rigidity of the cable, we may use the coefficient

k introduced above, so that

FkT,

FTF,

wherefrom

(4.2.29)

Figure 4.30. Equilibrium of exponential pulley blocks.

By means of fixed and movable pulleys, we may constitute systems of pulleys. We

mention thus the exponential pulley block (Fig.4.30,a), formed by a fixed pulley and

mobile ones, for which we have

Statics

257

(1 )

(4.2.30)

or, neglecting the frictions and the rigidity of the cables,

FF.

(4.2.30')

Analogously, for another exponential pulley block (Fig.4.30,b) we obtain

(

)

+−

(4.2.31)

−

FF.

(4.2.31')

Figure 4.31. Equilibrium of a pulley block with

fixed and

movable pulleys.

In the case of the pulley block with

n fixed and n movable pulleys (Fig.4.31), there

results

−

(1)

(4.2.32)

MECHANICAL SYSTEMS, CLASSICAL MODELS

258

(4.2.32')

With the aid of a hoist and of a mobile pulley we may obtain a differential pulley

block too.

2.1.7 Efforts in bars

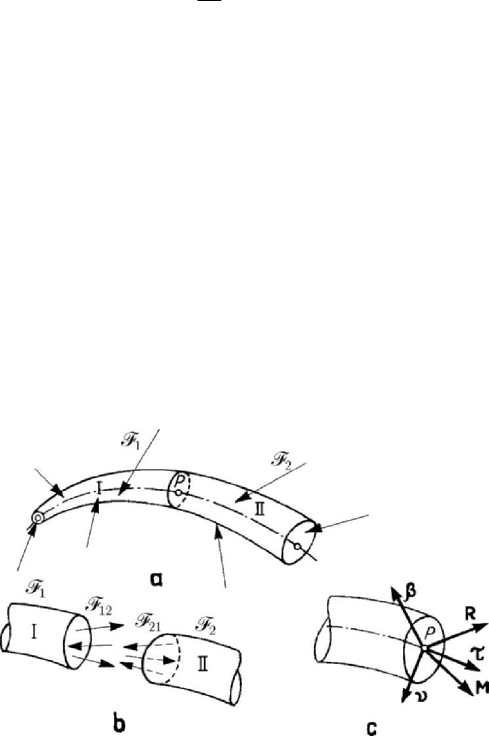
The notion of bar has been introduced in Chap. 1, Subsec. 1.1.10. Let thus be a

curved bar (the axis of which must be – in general – a skew curve) in equilibrium under

the action of a system

F of given and constraint external forces. A cross section (plane

and normal to the bar axis) divides the bar in two parts, and the internal forces which

arise on the two faces thus obtained are put into evidence (Fig.4.32,a,b). Thus, the part I

is acted upon by the subsystem

F of given forces and reactions and by the system

F of forces with which the part II is acting upon this one; analogously, the part II is

acted upon by the subsystem

F of given forces and reactions, as well as by the

system

F of forces with which the part I is acting upon it. The global condition of

equilibrium and the theorem of equilibrium of parts allow us to write

Figure 4.32. Equilibrium of a curved bar (a). Influence of the internal forces (b).

Resultant efforts on a cross section (c).

{}

+∼∼0FFF ,

{}

112

∼ 0FF ,

{}

221

∼ 0FF ,

(4.2.33)

wherefrom

{}

12 21

∼ 0FF ,

(4.2.33')

corresponding to the principle of action and reaction; as well, we get

21 1

∼FF,

12 2

∼FF

(4.2.33'')

Statics

259

too, so that we may state

Theorem 4.2.4. The system of internal forces by which a part of a bar acts upon the

other part is equivalent to the system of external (given and constraint) forces,

corresponding to the first part.

Applying the operator torsor (usually, at the centre of gravity of the cross section) to

the relations (4.2.33''), we get

{

}

{

}

21 1

τ=τFF,

{

}

{

}

12 2

=τFF;

(4.2.34)

the pole with respect to which has been made the computation was considered to be the

same for the two systems of forces (before the detachment of the two parts), so that we

did not put it in evidence. It is suitable to consider the torsor of the system of internal

forces corresponding to the face which is encountered the first by getting over the bar

axis. Frequently, one does it from left to right (part I), so that one has to do with the

torsor

{

}

τ F , corresponding to the left face. The components of the resultant R and

of the resultant moment

M are applied at the centre of gravity of this cross section

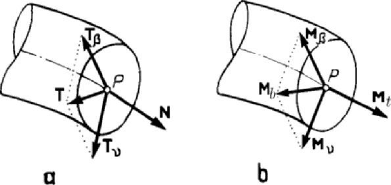
(Fig.4.32,c) and are called efforts (three forces and three moments); usually, Frenet’s

intrinsic trihedron is considered, the direction of the unit vector

of the tangent

coinciding with the direction of getting over the bar axis. The components of the

resultant

R are: The axial force N , along the tangent

, and the shearing (cross,

transverse) force

T , contained in the normal plane (of components T

and T

along

the principal normal and the binormal, respectively) (Fig.4.33,a). As well, the

components of the resultant moment

are: the moment of torsion (twisting moment)

, along the tangent, and the bending moment

, contained in the normal plane (of

components

and M

along the corresponding unit vectors) (Fig.4.33,b). By

Figure 4.33. Efforts on a cross section of a curved bar: force components (a)

and moment components (b).

convention, the scalars of these vector components are positive if they have the same

directions as the unit vectors of the axes of the intrinsic trihedron. We may thus write

=+ +R NT T

τνβ,

++M

MM M

νβ. (4.2.35)

The variation of the six efforts

,,, , ,

NT T M M M

νν

ββ

along the bar axis may be

represented by diagrams of efforts, which put in evidence their values in each section;