Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

230

system. The necessary and sufficient condition of equilibrium of a free rigid solid acted

upon by the given forces

{

}

F is written in the form

{

}

=F0,

∑

RF0,

×=

∑

MrF0;

(4.2.1)

one can thus state

Theorem 4.2.1. A free rigid solid subjected to the action of a system of given forces is

at rest (in equilibrium) with respect to a fixed frame of reference if and only if the

torsor of these forces with respect to an arbitrary pole vanishes.

Projecting the condition (4.2.1) on the co-ordinate axes, we get six conditions of

equilibrium

jij

∑

()

Oj jkl il

MxF

∈=

∑

, 1, 2, 3j

(4.2.1')

We notice that these scalar conditions may be replaced by other equivalent scalar

conditions. Thus, a free rigid solid is in equilibrium if and only if the sum of the

moments of all the given forces with respect to each of the edges of a non-degenerate

tetrahedron (the six straight lines do not belong to the same complex of first degree)

vanishes. Obviously, these conditions are necessary. Let us suppose that they hold for a

tetrahedron

123

OA A A . Because the sum of the moments with respect to the edges

OA ,

OA is zero, it follows that the moment with respect to the pole O is zero too; in

this case, the given forces are in equilibrium or have a unique resultant, which passes

through

O . This reasoning may be repeated for all the vertices of the tetrahedron, so

that the given forces must be in equilibrium, because there cannot exist a unique

resultant passing through all four vertices; hence, the above mentioned conditions are

sufficient too. But these equations are not independent, hence they are not conditions of

equilibrium for the free rigid solid if: three of the straight lines are concurrent or

parallel and coplanar at the same time (in particular, two of the straight lines are

parallel, while a third one is the straight line at infinity of the plane defined by the first

two ones or three of these straight lines are concurrent straight lines at infinity), four of

the straight lines are generatrices of the same family of a ruled quadric (in particular,

they can be concurrent or parallel), five of the straight lines intersect two other straight

lines or intersect a same straight line and are parallel to the same plane (they belong to a

linear congruence) or the six straight lines intersect the same straight line or are parallel

to the same plane (they belong to a linear complex).

In particular, in the case of a system of coplanar forces acting upon the free rigid

solid, three of the equations (4.2.1') are identically verified; there remain two equations

for the resultant

R (projections on two non-parallel axes in the plane of the forces) and

an equation of moment with respect to an axis normal to the considered plane.

Corresponding to the results in Chap. 2, Subsec. 2.2.6, we may replace these equations

by three equations of moment with respect to three non-coplanar axes, normal to the

plane of forces; as well, we may use two equations of moment with respect to two axes

normal to the plane of forces and an equation of projection of their resultant on an axis

Statics

231

contained in this plane and which is not normal to the plane of the other two axes. If the

above mentioned conditions are not fulfilled, then one of the scalar equations is a linear

consequence of the other two ones.

Corresponding to the results in Chap. 2, Subsec. 2.2.7, in the case of a system of

parallel forces, one can use for the resultant an equation of projection on the common

direction of the forces and one may write two equations of moment with respect to two

non-parallel axes, normal to this direction; we can use also three equations of moment

about three non-concurrent and non-parallel axes, contained in a plane normal to the

direction of the forces.

1,2,...,6n =

, then one can put into evidence some necessary conditions of

equilibrium of the free rigid solid, which must be verified a priori and which depend on

the geometric configuration of the given system of forces. So, a system formed of only

one non-zero force cannot be in equilibrium. A system of two forces can be in

equilibrium only if the forces have the same support; as well, a system of three forces is

in equilibrium only if their supports are concurrent or parallel and coplanar. For

4n =

it is necessary that the supports belong to the same linear series of straight lines (e.g.,

generatrices of the same family of a ruled quadric – in particular, concurrent or parallel)

to be in equilibrium. A necessary condition of equilibrium for

is the belonging

of the supports of the forces to the same congruence of the first degree (for instance,

they intersect two straight lines or they intersect a straight line and are parallel to a

plane). A system of six forces is in equilibrium (necessary condition) if their supports

belong to the same complex of first degree (e.g., an intersection with the same straight

line or the parallelism to a same plane).

In the first basic problem, the forces which act upon the free rigid solid are

given, and one asks the position of equilibrium. As we have seen in Chap. 3,

Subsec. 2.2.3, a free rigid solid has six degrees of freedom; in this case, the

unknowns are the six parameters (eventually, the co-ordinates of a point of the rigid

solid and the three Euler’s angles), which specify the position of the rigid solid. If

the system of six equations of equilibrium is indeterminate, then there exists an

infinity of possible positions of equilibrium, while if this system of equations is

impossible, then such a position does not exist. These observations may be put in

connection with the considerations previously made, concerning the cases in which

one cannot have equilibrium or in which some necessary conditions of equilibrium

have been emphasized.

The second basic problem is that in which the position of equilibrium of the free

rigid solid is given, and the forces which must act upon it to maintain this position are

searched; obviously, one supposes that this system of forces depends on a certain

number parameters, which are the unknowns of the problem (the magnitudes and the

directions of the forces). The solution of the problem is, in general, indeterminate; if

certain conditions, which limit the number of the unknowns to six, are imposed, then it

is possible that the solution of the problem be determinate.

We mention the mixed basic problem too, in which the position of equilibrium of the

rigid solid is partially known, as well as the system of forces; in this case, the position

of equilibrium and the system of forces are searched.

MECHANICAL SYSTEMS, CLASSICAL MODELS

232

2.1.2 Statics of the rigid solid with ideal constraints

The six degrees of freedom of a free rigid solid may be partially or totally annulled

by the introduction of some constraints, which we suppose to be ideal. Applying the

axiom of liberation from constraints, there appear constraint forces (reactions);

supplementary unknowns are thus introduced, but less scalar parameters are necessary

to determine the position of equilibrium. Let us suppose that the rigid solid with ideal

constraints is acted upon by a system of given forces

{

}

, 1,2,...,

F and a system

of constraint forces

{

}

, 1,2,...,

jm=R

; in this case, the necessary and sufficient

condition of equilibrium reads

{

}

{

}

τ+τ =FR0,

=RR 0

=MM 0,

(4.2.2)

where we have introduced the torsor of given forces in the form

∑

Ri F,

OOkk

=×

∑

MirF,

(4.2.2')

while the torsor of constraint forces is given by

∑

Ri R,

OOk

==×

∑

MirR.

(4.2.2'')

We may thus state

Theorem 4.2.1'. A rigid solid subjected to ideal constraints is at rest (in equilibrium)

with respect to a fixed frame of reference if and only if the sum of the torsors of given

and constraint forces with respect to the same arbitrary pole vanishes.

Projecting on the co-ordinate axes, we get six conditions of equilibrium

ik jk

∑∑

() ( )

iq jq

kpq kpq

xF xR

∈+∈ =

∑∑

, 1, 2, 3k

(4.2.2''')

The basic problem is, in general, a mixed problem in which both the unknown

position of equilibrium and the constraint forces are searched. Let

p and q be the

number of unknown scalars necessary to determine the constraint forces and the

position of equilibrium, respectively. If in such a problem we have

6pq+=

, then

this one is, in general, determinate (however, it is possible that in some particular cases

(critical cases) be indeterminate), and we say that the rigid solid is statically

determinate (isostatic). If

6pq

> , then the problem is indeterminate, the rigid solid

being statically indeterminate (hyperstatic). We are limited by the mathematical model

chosen for the solid, so that the unknowns of the problem cannot be determined; if we

consider a deformable solid, closer to physical reality, completing thus the mathematical

model, then there arise supplementary relations which allow the complete solving of the

problem. If

6pq+<, then the problem is, in general, impossible from the point of

Statics

233

view of the rest with respect to a fixed frame of reference, and we have to do with a

mechanism (in some particular cases, for certain systems of forces, the equilibrium

could be possible). In what follows, we deal only with statically determined rigid solids.

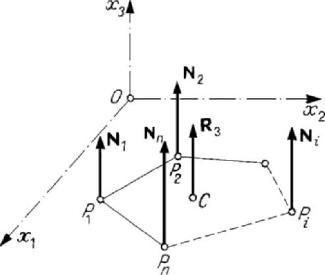
Figure 4.9. Polygon of sustentation.

Among the ideal constraints frequently encountered, we mention: the simple support,

the hinge (equivalent to three or two simple supports) and the built-in support

(equivalent to six simple supports), introduced in Chap. 3, Subsec. 2.2.10; taking into

account the above mentioned equivalences, we may consider the case of the rigid solid

on several simple supports too (in particular, the case of six simple supports), case

considered in the same subsection. Let thus be a rigid solid leaning on the plane

0x = at the points

() ()

(

)

,,0

Px x , 1,2,...,in

(Fig.4.9). The equations of

equilibrium are of the form

0RR

= ,

∑

()

MNx

∑

()

MNx

−

∑

where

N , 1,2,...,in= , are the unknown constraint forces. Hence, the external given

forces must verify the conditions

RRM

==, so that the rigid solid be in

equilibrium; these forces must reduce to a resultant

R , normal to the plane

0x = ,

because the scalar of the torsor vanishes (

). The other three equations

determine the constraint forces, and the problem is indeterminate if the number of the

points of support is greater than three. If

, then the given force

R must be

decomposed in three components of supports parallel to this force. We can mention,

e.g., the tripod of a painter or of a shoemaker; in case of a four-legged stool (

4n = ),

the problem is statically indeterminate (excepting the case in which the force

R acts at

the middle of the square

1234

PPPP ). The solution of the problem is determined if, for

3n = , the points

P ,

P and

P are not collinear; otherwise, the solution is

MECHANICAL SYSTEMS, CLASSICAL MODELS

234

indeterminate if the force

R pierces the straight line on which are the three points or

impossible if it does not pierce it. Hence, the rigid body simple supported on more than

two points, the reactions of which have supports parallel and coplanar, constitutes a

hyperstatic mechanical system. If the supports mentioned above are unilateral

constraints (as it happens in most cases), then

N > ,

1,2,...,in

; these reactions

are modelled by a system of parallel sliding vectors, their resultant

R being along the

central axis, which pierces the plane

at the point C of co-ordinates

()

∑

()

∑

There results that

() ()

min max

xxξ<< , 1, 2k

; hence, the point C is in the interior of

a convex polygon, which contains in its interior or on its contour the points

P ,

1,2,...,in= . The polygon of minimal area which fulfils these conditions is called

polygon of sustentation. Hence, to have equilibrium, the resultant of the external given

forces must pierce the plane of support (case of unilateral constraints) in the interior of

the polygon of sustentation.

Another important constraint, put in evidence in Chap. 3, Subsec. 2.2.10, is the

constraint by threads. This constraint is unilateral, introducing only one unknown (the

tension in the thread) if the direction of the thread is fixed. If the direction of the thread

may be anyone, then the constraint force has three unknown components; in this case, it

is possible that the thread does not introduce geometric restrictions (no constraints) for

the rigid solid (Fig.4.2,a) or may constrain the point of fixing of the same rigid solid to

stay on a curve or on a surface (Fig.4.2,b).

In the case of a system of coplanar given forces (e.g., contained in a plane

constx =

) remain only three conditions of equilibrium

∑∑

ik jk

FR, 1, 2k

() ()

()

() ()

()

21 2 1

12 1 2

ii j j

xF xF xR xR

−+ − =

∑∑

(4.2.3)

Analogously, if the rigid solid is acted upon by a system of parallel given forces (e.g.,

with supports parallel to the axis

Ox ), then the equations of equilibrium read

∑∑

()

iq jq

kpq kpq

xF xR

∈

+∈ =

∑∑

, 1, 2k

(4.2.4)

As in the case of a free rigid solid, the conditions of equilibrium may be expressed also

in other forms, equivalent to those above.

Statics

235

Figure 4.10. Equilibrium of a homogeneous heavy straight bar, which

leans on a vertical wall and at a fixed point.

Let be, for instance, a homogeneous straight bar of length

2l , which leans at A on a

vertical wall and at a fixed point

B , at a distance from the wall, which is acted upon

only by its own weight

G (Fig.4.10). We introduce the constraint forces N and H , so

that the bar be in equilibrium under the action of the given and constraint forces; for

equilibrium, the supports of the three forces must be concurrent. We write two

equations of moments with respect to the points

A and B and an equation of

projection of the forces on the vertical (we eliminate thus a constraint force from each

equation), in the form

sin 0

sin

NGlα

−

= , cot ( sin ) 0Ha G l aαα

−

−=, sin 0NGα −=,

Figure 4.11. Equilibrium of a homogeneous heavy straight bar, leaned on

a body bounded by a semispherical surface.

where α is the angle made by the bar with the horizontal (the generalized co-ordinate,

which determines the position of equilibrium); we get

(

)

⎡

⎤

=−

⎢

⎥

⎣

⎦

sin

(4.2.5)

MECHANICAL SYSTEMS, CLASSICAL MODELS

236

obtaining thus the constraint forces (because

,0NH≥

, it results that the directions of

these forces have been correctly chosen) and the position of equilibrium. We notice that

the condition

al≤ must hold; in the limit case, the equilibrium is labile, and NG= ,

0H = .

We suggest to the reader the solving of the problem (Fig.4.11) (the equilibrium of a

homogeneous heavy straight bar leaned on a body bound by a semispherical surface).

In the general case of a rigid solid subjected to constraints without friction takes

place a relation of the form (3.2.39); interesting particular cases have been considered

in Chap. 3, Subsec. 2.2.10.

2.1.3 Statics of a rigid solid with a fixed point or axis

Let be a rigid solid with a fixed point (which may be a spherical hinge), subjected to

the action of given forces of torsor

{

}

{

}

=FRM; without losing anything from

the generality, we may assume that the pole

O is at the fixed point (Fig.4.12). One has

only one constraint force

R at this point, so that the equations (4.2.2) lead to the

conditions

Figure 4.12. Equilibrium of a rigid solid with a fixed point.

M0, (4.2.6)

which must be fulfilled by the given forces and which determines the position of

equilibrium, and to the constraint force

−RR.

(4.2.6')

If the fixed point is just the centre of gravity (

≡

), while the rigid solid is subjected

only to the action of its own weight

G , then the condition (4.2.6) is identically

fulfilled, and we have

=−RG; the rigid solid is thus in equilibrium in any position,

the respective property being characteristic for the centre of gravity.

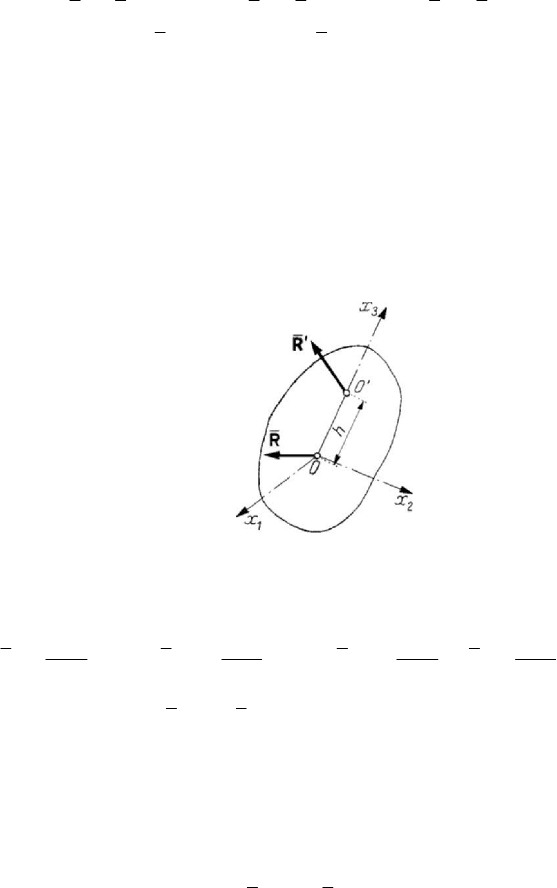
Let us consider a rigid solid which, besides the fixed point

O , admits another fixed

point

′

; in this case, the axis OO

′

is a fixed one, and we have to do with a rigid solid

with a fixed axis (taken as axis

Ox ) (Fig.4.13). The two fixed points at which, due to

the system of given forces, appear the constraint forces

R and

′

R , may be spherical

hinges. The equations (4.2.2) read

′

++ =RRR 0

′

×=MhR0

(4.2.7)

Statics

237

where

′





h , h being the distance between the two fixed points; in a developed

form, we may write

111

0RRR

′

+=,

222

0RRR

′

+=,

333

0RRR

′

+=,

MhR

′

−=,

MhR

′

= ,

(4.2.7')

For the equilibrium of a rigid solid with a fixed axis it is necessary and sufficient that

the resultant moment of the system of given forces with respect to this axis be equal to

zero (

M =

). As the corresponding equation of condition is compatible

(determinate or indeterminate) or incompatible, the rigid solid admits positions of

equilibrium (determinate or indeterminate – equilibrium in any position) or does not

allow such a position. Such a condition is fulfilled if the supports of all the given forces

intersect the fixed axis (e.g., the rigid solid with a fixed axis, the centre of gravity of

which is on this axis (

COO

′

∈ ), if it is acted upon by its own weight).

Figure 4.13. Equilibrium of a rigid solid with a fixed axis.

The components of the constraint forces are given by

=−

=− −

′

=−

′

;

(4.2.7'')

the other components (

R and

′

) are linked by the third relation (4.2.7') and cannot

be obtained independently, but only by renouncing to the hypothesis of rigidity (hence,

using another mathematical model of the solid). Indeed, one can apply at

O a force F

along the fixed axis and at

′

an analogous force

−

F , without any influence on the

mechanical phenomenon (in the case of the rigid solid, the forces are modelled by

sliding vectors); consequently, the components of the constraint forces along the

Ox –

axis are modified. Hence, the considered mechanical system is hyperstatic. To can

determine the constraint forces

R and

′

, a supplementary relation is necessary,

which may be obtained only by considerations concerning the deformation of the solid,

hence admitting another mathematical model of it. On the other hand, if at one of the

fixed points, for instance at

′

, we replace the spherical hinge by a cylindrical one,

along the fixed axis, then the problem becomes statically determinate (indeed, we have

MECHANICAL SYSTEMS, CLASSICAL MODELS

238

′

= , hence

RR=− ). If we impose the condition that the constraint force at O

′

be equal to zero for any position of equilibrium, then we get

= ; hence,

the system of given forces must be reduced to a resultant passing through the fixed

point

O (in this case, the rigid solid with a fixed axis behaves as a rigid solid with a

fixed point).

2.1.4 Statics of the rigid solid with constraints with friction

We have seen in Chap. 3, Subsec. 2.2.12 that, in reality, the solids are deformed in

the vicinity of the theoretical point of contact, so that the constraint forces which arise

have also tangential components, appearing moments (couples) too; thus, the

constraints with friction are put into evidence. The general case (Fig.3.33) leads to the

sliding friction (which hinders the displacement in the tangential plane), the pivoting

friction (which hinders the rotation about the normal to the tangential plane) and the

rolling friction (which hinders a rotation about an axis in the tangent plane).

The conditions of equilibrium will be, in general, of the form (4.2.2)-(4.2.2''), but as

in the case of one particle, the sign “=” is replaced by the sign “

≤

”, so that the

equalities become inequalities in the formulae (4.2.2). Thus, a certain zone of

equilibrium is emphasized, as well as a domain of variation of the given forces for these

positions of equilibrium. Practically, one considers firstly the case of the limit

equilibrium; then, one passes to the case indicated by the inequality which is modelling

the mechanical phenomenon. The three types of friction mentioned above have many

applications in technique; we consider some of these ones in what follows, especially

those which have interesting theoretical implications.

Concerning the sliding friction, we mention – especially – the possibility to use a

quadrangle of friction to study the equilibrium of a rigid solid leaning at two points on

other two solids and acted upon by forces coplanar with these points. In what concerns

the pivoting friction, we have considered the fundamental case of a vertical shaft of

circular or annular section (a rigid solid of cylindrical form) on a bearing. One may thus

study the case of an axially symmetric axle tree, the supports of which have analogous

properties; this last problem is much more difficult, its solution requiring some

supplementary hypotheses (a certain mathematical modelling).

A fundamental case of rolling friction is that of the drawn wheel (of radius

R and

weight

G ) of a vehicle by the horizontal force F (Fig.4.14,a). The imposed

conditions of equilibrium lead to

, TF

MFR

N−≤T ≤

N ,

sN M−≤ sN≤ , where

is the coefficient of sliding friction, while s is the

coefficient of rolling friction; hence, we have determined the normal constraint force

N , the sliding constraint force T and the rolling moment

M , and we have

emphasized the possibility of sliding and rolling in both directions. The conditions of

equilibrium will be thus of the form

GFfG

−

≤≤ and

(/ ) (/ )Gs R F Gs R−≤≤ ; as a matter of fact, one must fulfil the condition for

which the limits are the closest. The wheel begins to move by sliding or by rolling if

the force

F does not verify the first of those conditions, and we have /

sR< , or

the second one, and we have

sR> , respectively.

Statics

239

Analogously, we may consider the motive wheel (of radius

R and weight G ), acted

upon, besides the traction force

F , by the turning couple of moment M (Fig.4.14,b).

From the conditions of equilibrium, we get

, TF

MMFR=− ,

FfN≤ ,

sN M sN

−

≤≤, where we have emphasized the two tendencies of rolling

and only one of sliding, in an opposite direction with respect to the turning couple. We

obtain thus

FfG≤ and sG M FR sR

−

≤− ≤ or

[

]

(/ )FGsRR M

−

≤

[

]

(/ )FGsRR≤+ . Therefrom, we get the minimal turning couple

[

]

(/ )FGsRR=+ necessary to put the wheel in motion; the maximal traction force

FfG= . If

is greater than this magnitude (hence, if the horizontal plane is too

smooth – the coefficient too small), then the traction is not possible, no matter how

much greater is the turning couple

M .

Figure 4.14. The drawn (a) and the motive (b) wheel on a horizontal plane.

The case of the drawn wheel of a vehicle on a plane inclined by the angle

α with

respect to the horizontal (Fig.4.15,a) may be studied in the same manner. Thus, one can

show that if

sR< or /

sR> , tan

, then the wheel begins to move by

sliding or by rolling, respectively; but the force

F must not verify the condition of

equilibrium

sin( ) sin( )

cos cos

GFG

αϕ αϕ

ϕϕ

−+

≤≤

(

)

(

)

sin cos sin cos

GFG

αα αα−≤≤+,

respectively. If a turning couple of moment

M is introduced (Fig.4.15,b), then the

conditions of equilibrium are

sin( )

cos

ϕα

−

≤

and