Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

210

()

u u uu u v uu

′′ ′′ ′′′′

=− ⋅ = ⋅ =rn nr rrr ,

()

u v v u uv u v uv

′ ′ ′ ′ ′′ ′ ′ ′′

=− ⋅ =− ⋅ = ⋅ =rn rn nr rrr ,

()

vv vv uvvv

′′ ′′ ′′′′

=− ⋅ = ⋅ =rn nr rrr ,

(4.1.18')

with the notations

′

=∂ ∂nn, /

′

∂∂nn,

′′

∂∂rr,

′′

=∂ ∂ ∂rr,

′′

=∂ ∂rr; the expression in the second member of the relation (4.1.18)

represents the second basic quadratic form of the surface.

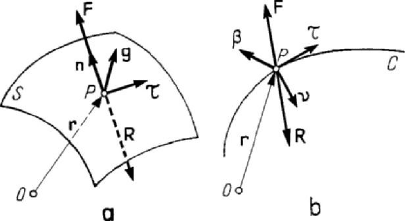
Let be a curve

C on the smooth surface S and a point P on this curve; the radius

of curvature of this curve at the point

P will be denoted by ρ . The plane determined

by the unit vectors

τ and n pierces the surface S by a curve

C , called the normal

section associated at

P to the curve C , the unit vector of the corresponding principal

normal being

ν ; the curvature 1/

ρ of the normal section

C associated at P to the

curve

C is called the normal curvature of the curve C at P and is positive or negative

(, ) 0

=) n ν or (, )

) n ν , respectively. We state thus

Theorem 4.1.1 (Meusnier). The normal curvature of a curve C on a surface S is the

projection of the curvature vector

/ ρ

on the unit vector n of the normal to the

surface

1cos

ρρ

= .

(4.1.19)

A unit vector

τ to which corresponds a zero normal curvature defines an asymptotic

direction; the curves on the surface for which the tangent to each point is an asymptotic

direction are called asymptotic lines of the surface. On a smooth surface

S there exist

two families of asymptotic lines determined by the differential equation

d2dd d0Lu Muv Nv

+=;

(4.1.20)

hence, through a point

(,)Puv of the surface pass two asymptotic lines. If a straight

line lays on a surface, then this one is obviously an asymptotic line. The projection of

the curvature vector

/ ρν on the tangent plane to a surface

at the point

is called, by

definition, the geodesic curvature of the curve

at the point

and is given by

()( )

1sin

(), (), () (), (), ()

sss s ss

ρρ

′′′′

==± =±ττ nrrn

;

(4.1.21)

one can prove that the geodesic curvature at a point

P of a curve C laying on the

surface

S is equal to the curvature of the projection of the curve C on the tangent

plane to the surface at the very same point

P . The radius

ρ is called radius of

geodesic curvature (or tangential). The geodesic curvature of the curve

C at a point P

Statics

211

is an intrinsic invariant of the surface

S . Let be a curve C for which the principal

normal

ν coincides with the normal n to the surface; in this case, the osculating plane

to the curve at the point

P is normal to the surface at this point, and we have

sin 0θ = , hence the geodesic curvature vanishes. The curves on the surface for which,

at any point, the geodesic curvature vanishes are called geodesic lines; the geodesic

lines of a smooth surface

S are determined by the differential equation

(

)

d,d , 0

rrn ,

(4.1.22)

so that through an ordinary point

P of it passes an infinity of geodesic lines. A

geodesic line passing through two points of the surface

S represents the shortest way

between these two points; it is a property of variational nature. For instance, the

geodesic lines on a sphere are its great circles. We introduce also the geodesic torsion

of the curve

C at the point P

11d

ρρ

=−

′

(4.1.23)

where

′

is the radius of geodesic torsion; we notice that the geodesic torsion of a

curve

C at a point P of the surface is equal to the torsion of the geodesic line tangent

to this curve at the point

P .

Returning to Darboux’s trihedron and introducing also Frenet’s trihedron, which

corresponds to a curve

C on a surface S , we may write

cos sinθθ=+νβn , sin cosθθ

−

βg , (4.1.24)

wherefrom

sin cosθθ=+ν gn, cos sinθθ

−+

gn. (4.1.24')

Starting form the Frenet’s formulae (4.1.10)-(4.1.10''), using the formulae (4.1.24),

(4.1.24'), and introducing the normal curvature (4.1.19), as well as the geodesic

curvature (4.1.21) and the geodesic torsion (4.1.23), we may write the derivatives of the

unit vectors of Darboux’s trihedron with respect to the arc

s in the form

d11

()

ρρ

′

==+

ng,

()

ρρ

′

==−−

′

d11

()

ρρ

′

==−+

′

(4.1.25)

MECHANICAL SYSTEMS, CLASSICAL MODELS

212

1.1.5 Particle subjected to ideal constraints

The ideal (smooth, frictionless) constraints are these constraints for which =T0; in

this case, the relation (3.2.36) takes place (the virtual work of the constraint forces

vanishes). In reality, such constraints do not exist; but there exist curves and surfaces

(constraints of contact) for which the force of friction can be neglected in a first

approximation. In this case, the reaction

(4.1.26)

is along the normal to the surface or is contained in the plane normal to the curve,

respectively, at the point at which stays the particle. Taking into account the condition

of equilibrium (4.1.4) and the relation (4.1.26), we may state

Theorem 4.1.2. A particle constrained to stay on a fixed smooth surface (curve) (ideal

constraints) is in equilibrium if and only if the resultant of the given forces acting upon

it is directed along the normal to the surface or is contained in the plane normal to the

curve, respectively, at the point which represents the position of equilibrium.

In the case of the particle subjected to ideal constraints, there appear unknowns

concerning the position of equilibrium and unknowns corresponding to the constraint

forces. The system of equations (4.1.4') is – in general – sufficient to solve the

equilibrium problem; but in some particular cases, this system can be indeterminate or

impossible, thus existing an infinity of such positions or none.

Figure 4.6. Particle in rest on a surface (a) or on a curve (b).

If the particle

P is constrained to stay on a fixed smooth surface S (Fig.4.6,a), of

equation (given in an implicit form)

(

)

123

() , , 0

fxx x

≡

=r ,

(4.1.27)

then the constraint force, normal to the surface, is of the form

grad

λ=R

Rfλ

1, 2, 3j

(4.1.27')

where the scalar

λ is a parameter which must be determined; we get the equations of

equilibrium

grad

λ+=F0

Ffλ

= ,

1, 2, 3j

. (4.1.27'')

Statics

213

The system of equations (4.1.27''), considered in the unknown

λ , is compatible if and

only if

123

,1 ,2 ,3

FFF

;

(4.1.27''')

these equations, together with (4.1.27), specify the position of equilibrium, while the

parameter

λ (hence, the constraint force (4.1.27')) is given by the system (4.1.27'').

If the equation of the surface

S is given in the explicit form

(

)

312

,xxxϕ

(4.1.28)

then we get the equations which determine the constraint force

1,1

0F λϕ+=,

2,2

0F λϕ

= ,

3,3

0F λϕ

= , (4.1.28')

while the conditions specifying the position of equilibrium are

,1 ,2

ϕϕ

=−

(4.1.28'')

Analogously, if the surface

is given by the parametric equations

(

)

xxuv

[

]

,uuu

∈

[

]

,vvv

∈

1, 2, 3i

(4.1.29)

then the conditions of equilibrium become

() () ()

123

23 31 12

,,,

det det det

(,) (,) (,)

FFF

xx xx xx

uv uv uv

∂∂∂

⎡⎤⎡⎤⎡⎤

⎢⎥⎢⎥⎢⎥

∂∂∂

⎣⎦⎣⎦⎣⎦

(4.1.29')

where we have put into evidence the director parameters of the normal in the form of

functional determinants, while the constraint force is given by the equations

(

)

det 0

2(,)

ijk

∂

⎡⎤

+∈ =

⎢⎥

∂

⎣⎦

, 1, 2, 3i

(4.1.29'')

where

ijk

∈

is Ricci’s symbol. Using Darboux’s local frame of reference, we notice that

==,

RR= , so that

= , 0

− ; (4.1.30)

the first two relations (4.1.30) state the position of equilibrium, while the last relation

specifies the constraint force.

MECHANICAL SYSTEMS, CLASSICAL MODELS

214

If the particle

P lies on a fixed smooth curve C (Fig.4.6,b) of equations (in an

implicit form)

(

)

123

() , , 0

fxxx≡=r ,

1, 2k

(4.1.31)

then one obtains the constraint force (in the plane normal to the curve

C , specified by

the normals to the surfaces passing through this curve)

1122

grad grad

fλλ=+R ,

11, 22,

Rf fλλ

+ ,

1, 2, 3j

, (4.1.31')

where the scalars

λ , 1, 2k = , are parameters to be determined, and the equations of

equilibrium

1122

grad grad

fλλ++ =F0,

11, 22,

Ff fλλ

+=, 1, 2, 3j

. (4.1.31'')

The system of linear equations in the unknowns

is compatible if and only if

11,12,1

21,22,2

31,32,3

Ff f

(4.1.31''')

obtaining thus the condition which, together with (4.1.31), specifies the position of

equilibrium; the parameters

λ ,

λ (hence, the constraint force (4.1.31')) are

subsequently determined by the system (4.1.31'').

If the equations of the curve

C are given in the explicit form

(

)

312

,xxxϕ= ,

(

)

312

,xxxψ

(4.1.32)

then we get the equations which give the constraint force in the form

11,12,1

0F λϕ λ ψ++ =,

21,22,2

0F λϕ λψ

+=,

312

0F λλ

−

−=, (4.1.32')

the condition specifying the position of equilibrium being

(

)

(

)

(

)

1 ,2 ,2 2 ,1 ,1 3 ,1 ,2 ,2 ,1

0FFFψϕ ϕψ ϕψϕψ−+ −+ − =.

(4.1.32'')

Analogously, for the parametric form of the curve

()

xxq= ,

[

]

,qqq

∈

1, 2, 3i

(4.1.33)

the components of the constraint force must fulfil the condition (the constraint force is

contained in the plane normal to the curve

C , hence it is normal to the tangent of

director parameters

()

′

1, 2, 3i

)

() 0

Rx q

′

(4.1.33')

Statics

215

This relation is identically fulfilled if

ijk k

Rxλ

′

=∈

, 1, 2, 3i

(4.1.34)

where

λ , 1, 2, 3j = , are arbitrary parameters; the equations of equilibrium become

ijk k

Fxλ

′

+∈ = ,

1, 2, 3i

(4.1.33'')

and are compatible if

() 0

Fx q

′

(4.1.33''')

The condition (4.1.33''') determines the values of the parameter

[

]

,qqq

∈

, which

correspond to the position of equilibrium. In this case, the system (4.1.33'') leads to

ijk

′

=+∈

′

, 1, 2, 3i

(4.1.34')

where

k is an indeterminate parameter; replacing in (4.1.34), we find the constraint

forces in the form

− , 1, 2, 3i

. (4.1.34'')

Using Frenet’s frame of reference, we notice that

, so that

= , RF

νν

− , RF

ββ

− ; (4.1.35)

the first of these relations gives the position of equilibrium, while the other two

relations specify the constraint force.

In the particular case of a heavy particle

P , constrained to stay on a fixed smooth

circle in a vertical plane (Fig.4.3,a), we have to do with an ideal constraint; the

constraint force is reduced to the normal component (

T0), and the equation of

equilibrium is of the form

=GN 0. (4.1.36)

Taking into account the Theorem 4.1.2, there results that the positions of equilibrium

are the points

P and

P ; the normal reaction is given by

−NG. (4.1.36')

In general, as it was shown in Chap. 3, Sec. 2.2, the particle

P is subjected to

holonomic, scleronomic constraints of the form

(

)

123

,, 0

xxx

, 1, 2l

(4.1.37)

MECHANICAL SYSTEMS, CLASSICAL MODELS

216

or to scleronomic, non-holonomic ones of the form

⋅

=rα , 1, 2k

; (4.1.37')

the total number of constraints may be at the most two. If we should have three

constraints, then the particle would be at a fixed point. We notice also that the particle

may be subjected only to holonomic constraints (as it was considered above) or only to

non-holonomic constraints or to a holonomic constraint and to a non-holonomic one. In

the case of ideal constraints, the virtual work of the constraint forces vanishes

=⋅δ=Rr , (4.1.38)

while the constraint force is given by the formula (3.2.37) in the form

grad

ll kk

fλμ

∑∑

R .

(4.1.38')

We notice that the first sum corresponds to the cases in which the particle is constrained

to stay on a fixed smooth surface or curve; the constraint force is expressed only with

the aid of the second sum if only non-holonomic constraints appear. The equations of

equilibrium are of the form

11221122

grad grad

fλλ μμ++++=

αF0, (4.1.39)

and only one or two of the four indetermined parameters

λ ,

μ ,

μ (the vector

coefficients of the other three or two parameters are equal to zero, because the

corresponding constraints do not take place) are involved. In the general case, the

problem is solved as it was shown above (the cases in which only one indeterminate

parameter

λ is involved or only two indeterminate parameters

λ ,

λ are involved).

1.1.6 Particle subjected to unilateral ideal constraints

We admitted, in the previous subsections, that the constraints are bilateral.

Analogously, the unilateral holonomic, scleronomic constraints of a particle may be

expressed in the form

(

)

123

,, 0

xxx ≥ , 1, 2l

(4.1.40)

and the unilateral non-holonomic, scleronomic ones in the form

⋅

≥α r , 1, 2k

, (4.1.40')

their total number being at the most equal to two; if three constraints should be, then the

particle would be at a fixed point, and all the relations would be equalities. As in the case of

bilateral constraints, the particle may be subjected only to holonomic or only to non-

holonomic constraints or to a holonomic constraint and to a non-holonomic one. As

Statics

217

it was shown in Chap. 3, Subsec. 2.2.9, in the case of unilateral constraints, the virtual

work of the constraint forces given by the formula (4.1.38') is non-negative

=⋅δ≥Rr . (4.1.41)

To solve the problem of equilibrium of a particle subjected to unilateral ideal

constraints, the positions of equilibrium are firstly determined, supposing that the

constraints are bilateral (equality in relations (4.1.40), (4.1.40')); then, the direction of

the resultant

F is analysed for each of these positions. If this direction ensures the

constraint, then the position of equilibrium is possible; otherwise, the positions of

equilibrium thus obtained do not correspond to the imposed constraints.

In the case of a particle which verifies a condition of the form

(

)

123

,, 0

xxx ≥ ,

(4.1.42)

the constraint force is given by

grad

, 0λ ≥ , (4.1.42')

and is directed along the normal to the surface

(

)

123

,, 0

xxx

, in the direction in

which the function

is increasing, as well as its gradient (to respect the imposed

unilateral constraint). As it is shown by the condition (4.1.4), for equilibrium one must

have

0⋅<FR , so that

grad 0

⋅

(4.1.42'')

or, in components,

. (4.1.42''')

In general, in the case of unilateral constraints (4.1.40), (4.1.40'), the equation of

equilibrium (4.1.39) leads, on the same way, to the conditions

(

)

221122 1

grad grad 0

fλμμ+++⋅<

αF ,

(

)

111122 2

grad grad 0

fλμμ+++⋅<

αF ,

(4.1.43)

(

)

1122221

grad grad 0

fλλ μ+++⋅<

αF ,

(

)

1122112

grad grad 0

fλλ μ+++⋅<

αF ,

(4.1.43')

where

12 1 2

,,, 0λλμμ≥ (in fact, only two of these conditions take place, because one

can have only two unilateral constraints).

Let be, for instance, the case of a particle of weight

G , linked by a flexible and

inextensible thread of length

l to a fixed point O and constrained to stay on the

vertical plane

Ox x (Fig.4.3,a); hence, the particle must be on a circle in this plane or

in its interior, satisfying the condition

MECHANICAL SYSTEMS, CLASSICAL MODELS

218

()

222

12 1 2

xx l x x

−−≥.

(4.1.44)

Noting that

0FF==,

− , assuming that the constraint is bilateral and

associating the constraint relation

, the condition (4.1.31''') reads

020

20 2 0

001

Gx Gx

−

−− =− =

so that the positions of equilibrium are the points

(0, , 0)Pl and

(0, , 0)Pl− (the same

positions as in the previous subsection); the condition (4.1.42''') becomes

0Gx < , and

is verified only at the point

P , which is the only position of equilibrium corresponding

to the unilateral constraint.

1.1.7 Notions concerning the stability of equilibrium

Let P be a particle of position vector ()t

rr. If

is an initial moment, then

we say that

const==

JJJJG

rc is a position of equilibrium if

(

)

t =rc,

(

)

()tt=⇒ ≡



r0rc; hence, if the particle P is at the mentioned position with zero

velocity, then it remains at any moment at this position. Taking into account the form

(1.1.95) of the force

F , Newton’s equation (1.1.89) leads – in this case – to

(, ;)t

Fc0 0

(4.1.45)

for a free particle. If this force depends on time, then the equation (4.1.45) has not, in

general, a constant solution (the same for any

); if the force does not depend on time,

then the equation (4.1.45) represents the necessary and sufficient condition of

equilibrium and one can obtain the vector

c .

We say that the position of equilibrium is stable if

0, 0εε

′

∀

>>, 0, 0ηη

′

∃> >

so that

(

)

t η−<rc,

(

)

()ttηε

′

⇒−<



rrc, ()t ε

′



r ,

tt∀> ; hence,

perturbing the position of equilibrium in a sufficiently small neighbourhood with a

sufficiently small velocity, this position remains at any moment in a previously given

neighbourhood, and its velocity is not greater than a certain limit, previously given too.

Otherwise, the position of equilibrium is instable, and can be labile or, at the limit,

critical; in the latter case, the equilibrium can be indifferent (any position of the particle

is a position of equilibrium).

For instance, in the particular case considered in Subsec. 1.1.2, one finds easily that

P represents a labile position of equilibrium, while

P is a stable one (Fig.4.3,a); if,

passing to the limit (

l →∞), the circle becomes a horizontal straight line, then any

position is a position of equilibrium (the equilibrium is indifferent). We notice that, in

the considered case, the particle has a minimal, maximal, or stationary

x – co-ordinate,

as we are in a stable, labile, or indifferent case, respectively; we are thus led to

Statics

219

Theorem 4.1.3 (E. Torricelli). The position of equilibrium of a particle subjected only

to the action of a given uniform gravitational field is a stable, labile or indifferent

position of equilibrium as this one has a minimal, maximal, or stationary applicate,

respectively (with respect to a frame of reference for which one of the axes is parallel to

the considered field, opposite to its direction).

Let

be a free particle subjected to the action of a conservative force of the form

(1.1.82). The condition of equilibrium (4.1.2) becomes

1, 2, 3i

, (4.1.46)

corresponding thus to the necessary conditions to have an extremum of the potential

function

U . When passing to the curvilinear co-ordinates

q , 1, 2, 3i

, by relations

of the form (A.1.32), we may write (

()()()

123 123

,, ,,Uqqq Uqqq=r )

d grad d d d grad d

ii j

UUUxUq

∂

⋅= ⋅= = = ⋅ =

∂

Fr r

ij j

Uq q

∂

∂∂

;

hence, the conditions of equilibrium (4.1.46) are equivalent to the conditions

∂

, 1, 2, 3j

(4.1.46')

in curvilinear co-ordinates.

In the particular case considered above, the gravity force

G is conservative and

derives from the potential

UGx

− (the additive constant is taken equal to zero).

With the aid of Torricelli’s theorem, we notice that the minimal applicate of the particle

P corresponds to a maximum of the potential U , while the maximal one corresponds

to a minimum of it; if the applicate of the particle is stationary, then the potential

enjoys this property too. We may state

Theorem 4.1.4 (Lagrange-Dirichlet). The position of equilibrium

P of a particle

subjected to scleronomic, holonomic constraints, acted upon by a field of conservative

forces, the potential of which has an isolated maximum at the point

, is a position of

stable equilibrium.

This theorem may be proved with the aid of the theorem of energy. Intuitively, let us

suppose that the potential

U of a free particle P has an isolated maximum equal to

at the point

P ;

UU< in the neighbourhood of

P , so that the equipotential surface

UU ε=−, 0ε > sufficiently small, is a closed surface surrounding the point

and reducing, by continuity, to this very point if

0ε → (Fig.4.7,a). The force

gradU=F is normal to the potential surface at each point of it and is directed in the

growing direction of

U , hence towards the interior of the surface; the considered force

does not allow the particle

P to move away from the position

P , so that this one is a

position of stable equilibrium.