Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

180

where

θ are forms of the first degree; the system of differential equations 0

ω = ,

1,2,...,km= , is completely integrable if there exist the functions

and

g , so that

kkj

gω

∑

(3.2.28)

, (3.2.28')

F being a non-singular matrix. One proves

Theorem 3.2.2 (Frobenius). The system of forms (3.2.28) is completely integrable if

and only if there exists a system of forms of the first degree

θ , so that

d =∧

ΘΩ,

kkj

ωθω

=∧

∑

, 1,2,...,km

(3.2.29)

The conditions (3.2.29) may be expressed also in an equivalent form (particularly

convenient for applications; the condition (3.2.26) is a particular case)

... d 0

ωω ω ω∧∧∧ ∧ =,

1,2,...,km

. (3.2.29')

In the particular case of the form

(

)

(

)

(

)

1 123 1 2 123 2 3 123 3

,, d ,, d ,, daxxx x axxx x axxx xω =++,

(3.2.30)

the condition of integrability becomes

123

ddd 0

ijk k j

aa x x x∈∧∧=. (3.2.30')

Indeed, the equation

0ω

is integrable if there exists an integrating factor

(

)

123

,,xxxλλ= , so that λa be a gradient, hence so that curl( ) curlλλ=aa

gradλ+×=a0; a scalar product by

leads to

curl 0

ijk k j

aa⋅=∈ =aa . (3.2.30'')

By analogy to the considerations of Subsec. 2.2.2 for the holonomic case, we can

state that the relations (3.2.13''') represent the conditions for the representative point

of a non-holonomic mechanical system to be at the intersection of

m non-holonomic

hypersurfaces (hypersurfaces studied by Gh. Vrănceanu) in the representative space

E , hence on a non-holonomic manifold of dimension 3rnm

− (equal to the

number of degrees of kinematic freedom) of this space.

In general, a mechanical system may be subjected to

p holonomic and to m non-

holonomic constraints; in the case of a discrete mechanical system we must have

Mass geometry. Displacements. Constraints

181

3pm n+<

. The number of degrees of freedom will be 3( )npm

−

+ (obviously,

kinematic degrees of freedom, because the holonomic constraints have the same

number of geometric and kinematic degrees of freedom). In the case of a non-

deformable mechanical system, one must have

6pm

, and the number of degrees

of freedom will be

6( )pm−+ , the holonomic and non-holonomic constraints being –

obviously – external.

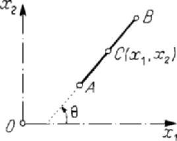
Figure 3.25. Motion of a rigid skate AB.

Let us consider, for instance, the motion of a rigid skate

AB on the ice plane,

considered to be the plane

Ox x

; let

be the middle of the segment AB (the

theoretic point of contact between the curved sole of the skate and the ice). Obviously,

the position of this segment is given by the co-ordinates

,xx of the point

and by

the angle

made by the segment AB with the axis

(Fig.3.25). The parameters

,xx and

are independent at a moment

, hence the skate has three degrees of

freedom in finite displacements. We notice that the trajectory of the point

is tangent

AB ; because the displacement of the point

(as well as its velocity) can take place

only along the direction

AB (to avoid a skipping), we may write the relation

tanxx θ

 , (3.2.31)

linking the components of the velocity of the point

C . Starting from the form

sin d cos dxxωθ θ

−

(3.2.31')

and using the formula (A.1.55), we can write

dcosdd sinddxxωθθ θθ=∧+∧; (3.2.31'')

hence, with the aid of the properties emphasized in App., Subsec. 1.2.1, one obtains

12 12

d sindddcosdddxx xxωω θ θ θ θ∧=− ∧ ∧− ∧ ∧

ddd0xxθ=− ∧ ∧ ≠ ,

(3.2.31''')

so that the constraint (3.2.31) is non-integrable, and the considered mechanical system

is non-holonomic. We may also suppose that the plane

Ox x is inclined with respect

to a horizontal one, taking the axis

Ox along the direction of maximal inclination.

A sphere or a plane disk (in a vertical plane), which is rolling without sliding on a

fixed horizontal plane may be other examples of mechanical systems subjected to

MECHANICAL SYSTEMS, CLASSICAL MODELS

182

non-holonomic constraints. We notice that in such a case the number

s of degrees of

freedom given by the finite displacements is greater than the number

r of degrees of

freedom given by the infinitesimal ones (

sr> ).

The constraints considered above are bilateral ones; in the case of unilateral

constraints, one can make analogous considerations, using – for instance – relations of

the form (3.2.16) or of the form

∇⋅δ≥

∑

r , 1,2,...,lp

(3.2.16

)

2.2.7 Scleronomic and rheonomic constraints. Catastatic constraints

If the temporal variable

t does not appear explicitly in the infinitesimal constraints

(3.2.13) or (3.2.13') (stationary case), hence if

∂



, 1,2,...,in

, 1,2,...,km

(3.2.32)

then these constraints are called scleronomic; otherwise they are called rheonomic (non-

stationary case). These conditions become

∂



1,2,...,3jn

1,2,...,km

(3.2.32')

in the representative space

E .

Taking into account (3.2.21'), we observe that it is sufficient to have



1,2,...,lp

(3.2.33)

so that these holonomic constraints be scleronomic too; they must be of the form

(

)

1,2,...,lp

(3.2.33')

We may also write

∇⋅ =

∑

r , 1,2,...,lp

(3.2.33'')

as well as a relation of the form (3.2.21'').

We notice that a constraint of the form (3.2.33') represents a fixed hypersurface; but

a rheonomic constraint of the form (3.2.8) may represent a rigid surface, moving with

respect to a rigid frame of reference, or a deformable surface.

We mention that the two classifications of the constraints (holonomic or non-

holonomic and scleronomic or rheonomic) are independent; we may have, for instance,

non-holonomic, rheonomic constraints (in the most general case) and holonomic,

scleronomic constraints (in the most particular case).

Mass geometry. Displacements. Constraints

183

Taking into account the relations (3.2.15) verified by the virtual displacements, we

notice that – in the case of scleronomic constraints – the set of virtual displacements

coincides with the set of possible displacements; as well, in this case the real

displacements belong to the set of virtual displacements. But these properties take place

also if one has only

bα ==, 1,2,...,km

. (3.2.32'')

These conditions are sufficient; it is not necessary that the constraints be scleronomic.

The constraints for which conditions of the form (3.2.32'') hold are called catastatic

constraints. These conditions do not impose with necessity



0 (or

b =



) if the

constraints are non-holonomic; holonomic, rheonomic constraints which have these

properties do not exist (in this case, the above condition holds too).

One can make analogous considerations in the case of unilateral constraints.

As examples of mechanical systems subjected to holonomic, scleronomic constraints

one can mention the rigid solid (or a non-deformable discrete mechanical system), the

points of which verify conditions of the form (3.2.22), the particle being constrained to

stay on a fixed curve or surface etc. If the curve (surface) is moving, then the constraint

is holonomic and rheonomic (for instance, a constraint of the form (3.2.10)); in general,

in the case of a relative motion we have to do – in fact – just with such a constraint. The

rigid solid with a fixed point or axis represents a holonomic and scleronomic

mechanical system. We may consider also systems of rigid solids, subjected to mutual

constraints (internal constraints), as well as to various external constraints. In a certain

manner, each rigid solid behaves in the respective mechanical system as a particle,

which has not three but six degrees of proper freedom.

The non-holonomic constraints of the previous subsection (for instance, the

constraint expressed by the relation (3.2.31)) are scleronomic constraints.

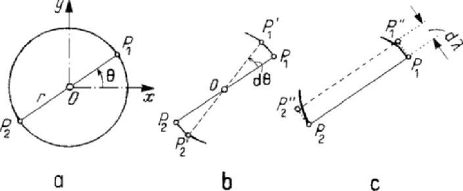
2.2.8 Critical constraints

If the number

s of the degrees of freedom given by the finite displacements is less

than the number

r of the degrees of freedom given by the infinitesimal relations

(

sr< ), then we have to do with critical constraints.

Let, for instance, be a mechanical system formed by two particles

and

linked

by a rigid bar of length

and constraint to be on a circle of radius r (Fig.3.26,a).

The constraint relations (holonomic and scleronomic) are of the form (in a fixed frame

of reference

Oxy )

22 22 2

11 22

xy xy r

=+=

()()

12 12

4xx yy r−+−=.

(3.2.34)

Because the four co-ordinates must verify three finite independent relations, it follows

that the mechanical system has one geometric degree of freedom (

1s = ) (in finite

displacements). Indeed, we see that these co-ordinates may be expressed by means of

the angle

θ , taken as an independent parameter, in the form

cosxxrθ=− = ,

sinyyrθ

−= . (3.2.34')

MECHANICAL SYSTEMS, CLASSICAL MODELS

184

By differentiation, one obtains

11 11

dd0xx yy+=,

22 22

dd0xx yy

= ,

(

)

(

)

(

)

(

)

12 1 2 12 1 2

dd dd 0xx x x yy y y−−+−−=;

(3.2.34'')

taking into account (3.2.34'), we notice that the last relation (3.2.34'') is a linear

consequence of the first two relations. Between the four co-ordinates take thus place

two differential relations, so that the considered mechanical system has two kinematic

degrees of freedom (

2r = ) (in infinitesimal displacements). The condition mentioned

above (

) is thus fulfilled. One can put into evidence an infinitesimal rotation dθ

(Fig.3.26,b), corresponding to a finite rotation

θ , as well as an infinitesimal translation

dλ (Fig.3.26,c), which has not any correspondent in finite displacements.

Figure 3.26. Critical system formed by two particles linked by a rigid bar and constrained to be

on a circle (a). An infinitesimal rotation dθ (b) and an infinitesimal translation dλ (c).

The fact that in case of critical constraints can take place infinitesimal displacements

which do not have correspondence in finite displacements characterizes the respective

constraints; indeed, this property corresponds to the above given definition.

2.2.9 Virtual work of constraint forces. Ideal constraints

We call system of possible accelerations of the particles

P ,

1,2,...,in

, of the

considered mechanical system

S any system of accelerations

a which satisfies, at a

moment

t , the relations (3.2.23), (3.2.23') and (3.2.24) (obtained from the holonomic

and non-holonomic constraints, respectively, to which may be subjected the system

S ),

supposing that the position (the position vectors

r ) and the velocities

v of the system

S verify the relations (3.2.8) and (3.2.13'), respectively. A system of accelerations

which does not satisfy all these conditions is called a system of impossible

accelerations. In the case of unilateral constraints analogous definitions can be given.

If the mechanical system

S is free, then any particle

P must satisfy an equation of

the form

ii i

aF, 1,2,...,in

, (3.2.35)

Mass geometry. Displacements. Constraints

185

corresponding to Newton’s law (1.1.89), where

F is the resultant of all the external

and internal given forces which act upon the respective particle. In these conditions, if

the accelerations

a form a system of possible accelerations for the considered

mechanical system

S with constraints, then the constraint relations represent particular

integrals of the equations of motion, having to do with a particular case of motion of

this mechanical system. In the case of a system of impossible accelerations, one must

introduce also the constraint forces

R , unknown a priori and acting upon the particles

P , 1,2,...,in= ; the equations of motion become

ii i i

m =+aFR, 1,2,...,in

. (3.2.35')

To obtain possible accelerations, one must determine the constraint forces

correspondingly; the mechanical system

S becomes thus a free one, subjected to both

given and constraint forces; in fact, this corresponds to the axiom of liberation from

constraints.

We notice that one must determine

6n unknowns ( 3n co-ordinates of the particles

of the system

S and

components of the constraint forces), with the aid of

scalar equations of motion (projections of the equations (3.2.35')) and

pm+

constraint relations (3.2.8), (3.2.13'); there are still necessary

6(3 )nnpm−++=3n ()pm

−

+ scalar equations (a number of relations equal to

the number of degrees of freedom) to solve the problem. To do this, we introduce an

important class of constraints: the class of ideal constraints. Thus, we call ideal

constraints these ones for which the virtual work of the constraint forces, given by

(3.2.7'), vanishes

⋅

δ=

∑

(3.2.36)

for any system of virtual displacements of the considered mechanical system

S .

If the virtual displacements

r are arbitrary (we have not constraints), the relation

(3.2.36) holds only if

=R0,

1,2,...,in

. Indeed, because the virtual displacements

are arbitrary, we may equate them to zero, unless one, let be

r ; the relation (3.2.36) is

reduced to

⋅δ =Rr . But the direction of

r is arbitrary, so that

=R0; taking

1,2,...,jn= , one is led to the above conclusion. In this case, the system of equations

of motion is sufficient to solve the problem.

But if

constraints of the form (3.2.21'') and m constraints of the form (3.2.15)

take place, we will use the method of Lagrange’s multipliers. Starting from the relation

(3.2.36) and with the aid of the relations (3.2.21'') and (3.2.15), we may write

11 1

ii i

ll kki

il k

fλμ

== =

⎛⎞

−

∇− ⋅δ=

⎜⎟

⎝⎠

∑∑ ∑

Rrα

MECHANICAL SYSTEMS, CLASSICAL MODELS

186

where

λ ,

1,2,...,lp=

, and

μ ,

1,2,...,km

, are non-determined scalars

(Lagrange’s multipliers) and where we took into account that in a double finite sum one

can invert the summation order; in components, we have

()

() ()

11 1

iii

il k

λμα

== =

⎛⎞

∂

−

−δ=

⎜⎟

∂

⎝⎠

∑∑ ∑

We introduce the notations (3.2.9) and we put thus into evidence

3n virtual

displacements

Xδ , 1,2,...,3jn= , which verify pm

linear and distinct constraint

relations (3.2.21''), (3.2.15), the matrix of the coefficients being of rank

pm+

(otherwise the constraint relations could not be distinct). We express the virtual

displacements

, ,...,

XX X

δδ δ

(we always may choose them so as the determinant

pm+

of the respective coefficients of the constraint relations be non-zero) with the aid

of the other

3( )npm−+ virtual displacements, so that the latter ones may be

considered as being independent. If we equate to zero the parentheses multiplying the

first

pm+ virtual displacements, then pm

multipliers

and

μ are univocally

determined (these multipliers are given by a system of

linear algebraic

equations with

pm+ unknowns, of determinant 0

pm+

≠ ). As in the case

previously considered, the independent virtual displacements

, ,...,

pm pm

++ ++

Xδ may all vanish, excepting only one, denoted by

; because this non-zero

displacement is arbitrary, it follows that the parenthesis multiplying it must vanish. If

successively

1, 2,..., 3jpm pm n=+ + + + , and if we take into account the

previous result, then all the parentheses multiplying the virtual displacements must

vanish; one obtains thus the

3( )npm

−

+ supplementary relations searched to may

solve the problem, so that the supplementary condition (3.2.36) introduced for the ideal

constraints is sufficient. Finally, we may write

ll kki

fλμ

=∇+

∑∑

, 1,2,...,in

(3.2.37)

The motion of the mechanical system

S as well as the constraint forces are completely

determined.

By means of the expression (3.2.37) of the constraint forces and of the constraint

relations (3.2.21), (3.2.13), we may write the real elementary work of the constraint

forces in the form

ddd

Rll kk

Wft tλμα

=− −

∑∑



(3.2.37')



1,2,...,lp=

and

1,2,...,km

(which holds, in general, in the

case of catastatic constraints or, in particular, in the case of scleronomic constraints, as

Mass geometry. Displacements. Constraints

187

we have seen in Subsec. 2.2.7), then the real elementary work of the constraint forces

vanishes; this result is justified also because the real displacements belong to the set of

virtual displacements, the relation (3.2.36) implying

If, in the case of unilateral constraints of the form (3.2.16

) or (3.2.16), the virtual

work of the constraint forces given by the relations (3.2.37) verifies the inequality

⋅

δ≥

∑

Rr ,

(3.2.36')

then these constraints are ideal ones; in this case one can make similar considerations to

the above ones too.

To put into evidence the importance of the class of ideal constraints, we will show

that a great number of mechanical systems belongs to this class. Let us consider a

particle

P constrained to stay on a fixed curve C (Fig.3.20,a) or on a fixed surface S

(Fig.3.20,b); if we assume that the constraint is without friction, then the constraint

force

R is normal to the curve or to the surface, respectively (a tangential component

would correspond to a sliding friction). Because the virtual displacement

δr takes

place along the tangent to

or in a plane tangent to

, it follows that 0⋅δ =Rr ;

taking into account (3.2.37), we notice that this relation is of the form (3.2.21''),

corresponding to the condition to which is subjected a particle constrained to be on a

fixed curve or surface, respectively. This affirmation holds also in the case of a

movable or deformable curve or surface (non-stationary case), because the constraint

force

R and the virtual displacement

r correspond to a fixed moment t ; we mention

that, in this case,

0⋅Δ ≠Rr , and the necessity to use virtual displacements instead of

possible ones is put into evidence. The constraints considered above are constraints of

contact.

In the case of constraints at distance, for instance in the case in which the distance

between two particles

P and

P is a function only on time (

()

ij ij

rrt

), we have

(Fig.1.18)

()()( ) ( )

220

ij ji ji j i ij j i

rδ=δ − = − ⋅δ−δ = ⋅δ−δ =rr rr r r r r r ,

because the virtual displacements do not take place in time; if the internal constraint

forces are of the form

ij ij

Rr,

iji

Rr,

ij ij

=RR 0, λ being an

indeterminate scalar, then the virtual work is given by

ij i ji j

⋅

δ+ ⋅δ =RrRr . In the

particular case in which

const

, we can state that a non-deformable discrete

mechanical system is subjected to ideal internal constraints.

The ideal constraints may be introduced axiomatically with the aid of the relations

(3.2.36), (3.2.36') in the case of a continuous mechanical system too, where the

constraint forces

R are applied at the points

P . As a consequence, a rigid solid is also

subjected to ideal internal constraints. In what concerns the external constraints, we

may consider various cases of such ones. Thus, a rigid solid with a fixed point leads to

a constraint force

R applied at the very same point of position vector r , hence to

0⋅δ =Rr (because δ=r0). In the case of two fixed points P and P

′

of position

MECHANICAL SYSTEMS, CLASSICAL MODELS

188

vectors

r and

′

r , respectively (a rigid solid with a fixed axis), we may write,

analogously,

′′

⋅δ + ⋅δ =RrR r . As well, in the case of a rigid solid sliding without

friction on a fixed or movable curve (or surface), constraint forces normal to the curve

(or surface) arise at the contact points of the rigid solid, while the corresponding virtual

displacements are along the tangent (or in the tangent plane); the condition of ideal

constraints is thus verified. The rigid solid which is rolling or pivoting without sliding

on a fixed surface (it is subjected to a rotation about an instantaneous axis of rotation

parallel or normal, respectively, to the tangent plane at the contact point), enjoys the

same property; we suppose in these cases that the rolling and pivoting friction,

respectively, vanishes.

Figure 3.27. Two rigid solids S and Σ tangent along perfectly smooth surfaces (a). Case of an

angular point (b). Representation of the simple support by a

pendulum (c) or by a small cart (d).

Let be a mechanical system formed by two rigid solids S and Σ , constrained to

remain tangent (one supposes that the surfaces in contact are perfectly smooth, the

solids sliding one on the other); at the contact point

()P r arise the constraint forces

=NN and

=−NN (on the basis of the principle of action and reaction,

S Σ

+=NN 0), which are normal to the considered surfaces (Fig.3.27,a). The relative

velocity of the two rigid solids at

P is

SΣ

−

vv (the difference between their

velocities), so that the difference of two possible displacements (which are virtual

displacements too)

(

)

ΣΣ

Δ−Δ= − Δrrvv lies in the common tangent plane; it

follows that

SS S SΣΣ Σ Σ

⋅δ+⋅δ=⋅Δ+⋅Δ=NrN rN rN r

()

SΣΣ

⋅Δ −ΔNrr

0= . If the surfaces in contact are rough, the rigid solids rolling one on the other

without sliding, then the relative velocity at the contact point vanishes (

SΣ

−=vv0);

we also get

(

)

SS SΣΣ ΣΣ

⋅δ + ⋅δ = Δ −ΔRrR rR r r

(

)

ΣΣ

⋅−ΔRvv 0= ,

because the constraint forces verify the relation

S Σ

=RR 0. Let be also the case in

which the two rigid solids are linked by a hinge at

()P r (Fig.3.28,a). If we neglect the

frictions, then the action of the rigid solid

Σ upon the rigid solid S is reduce to a force

R applied at P , while the action of the rigid solid S upon the rigid solid Σ is

reduced to a force

R , applied at P too; obviously,

S Σ

=RR 0. It follows that

Mass geometry. Displacements. Constraints

189

SS ΣΣ

⋅δ + ⋅δRrR r

()

S Σ

=+⋅δRR r 0

, because the point P has the same

virtual displacement

S Σ

δ=δ=δrr r, immaterial to which rigid solid it belongs.

Figure 3.28. Two rigid solids

and

linked by a hinge (a). Spherical hinge (b) represented

by three non-coplanar pendulums (c) or by an idealized fixed support (d).

In general, a mechanism is formed by a system of rigid solids, which are linked by

hinges or by supports on perfectly smooth or rough surfaces; because there are not

frictions, one may consider that this mechanical system is subjected to ideal constraints.

In the case in which arises also a sliding, a rolling or a pivoting friction, then one

must introduce the corresponding components of the constraint forces and one must

make supplementary hypotheses to allow the determination of these components; the

mathematical model of the system of constraints must be completed. One may thus

consider the motion with friction of a particle along a curve or a surface, the motion

with friction of a rigid solid on another one etc.

We notice that the relation

= , corresponding to ideal constraints, may be

written also in the equivalent form

∗

⋅

∑

Rv ,

(3.2.36'')

where we have put into evidence the virtual velocities of the points at which the

constraint forces are applied.

2.2.10 Ideal constraints of the rigid solid

As we have seen, a free rigid solid has six degrees of freedom. If some external

constraints appear, then the number

s of these degrees of freedom becomes smaller

(there is no more necessary the same number of independent parameters to specify the

position of the rigid solid); otherwise, applying the axiom of liberation of constraints,

one must determine the unknown constraint forces which are introduced, hence

unknown scalars. If in a given rigid solid problem one has

6sp

= , then this one is,

in general, determinate (excepting some particular cases in which it could be