Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

150

Let be the equation of the ellipsoid of inertia written in the form

2222

123 11 22 33

(, , ) 0

xxx IxIxIxK

++−=

Figure 3.9. The ellipsoids of inertia and of gyration.

and an arbitrary point

P of position vector r on this surface (Fig.3.9); the normal from

O to the plane tangent at P to the ellipsoid of inertia pierces this plane at

, so that

OQ h=

JJG

. We construct the inverse P

′

of the point Q with respect to a sphere of

centre

O and arbitrary radius R ; hence,

versOP r OQ

′′′

JJJG

JJG

grad

vers

grad

JJG

vershOQ OQ==⋅

JJG JJJG

r ,

rh R

′

= ,

the point

′

being of co-ordinates

123

,,xxx

′

′′

. It follows that

grad

′

⋅

(3.1.104)

wherefrom

123

11 22 33

xxx

Ix Ix Ix

′′′

===

(3.1.104')

The locus of the point

′

is an ellipsoid too (

KMR= )

222

123

222

123

xxx

iii

′′′

+=,

(3.1.105)

called the ellipsoid of gyration, where we have introduced the gyration radii. One may

pass from

′

to P by a similar graphic construction and by a formula of the form

(3.1.104), obtaining thus the ellipsoid of inertia; the two ellipsoids are reciprocal.

Let us consider a plane of axes of co-ordinates

and OI

ΔΔ

′

(Fig.3.10) and

three circles (Mohr’s circles):

C of centre

(

)

(

)

12 3

/2,0OI I

and radius

Mass geometry. Displacements. Constraints

151

()

123

/2RII=− ,

C of centre

(

)

(

)

231

/2,0OI I

and radius

(

)

213

/2RII=− and

C of centre

(

)

(

)

312

/2,0OII

and radius

(

)

312

/2RII=− . The co-ordinates of a point P in the hatched domain are an

axial moment of inertia

and a centrifugal moment of inertia I

ΔΔ

′

. One obtains a

plane geometric representation for a three-dimensional moment of inertia tensor; we

have thus the possibility to get – in a simple way – the extreme values of the axial

and centrifugal moments of inertia. For instance, the extreme centrifugal moments of

inertia are the radii of the three circles, that is

Figure 3.10. Mohr’s circles for axial moments of inertia (three-dimensional case).

()

III

ΔΔ

′

=± −

()

III

ΔΔ

′

′′

=± −

()

III

ΔΔ

′

′′′

=± −

(3.1.106)

while the corresponding axial moments of inertia are the abscissae of the centres of the

very same circles, (see also Subsec. 1.2.3), i.e.,

()

III

′

()

III

′′

()

III

′′′

(3.1.106')

Once the principal moments of inertia specified, the three circles are easily obtained.

Let be a direction of unit vector

n ; one can thus build up three arcs of circle of centres

O ,

O and

O , and of radii given by (Fig.3.11,a)

()()()

12311213

r II nIIII=−+ − −,

()()()

23122321

rIInIIII=−+ − −,

()()()

31233132

r II nIIII=−+ − −

;

(3.1.107)

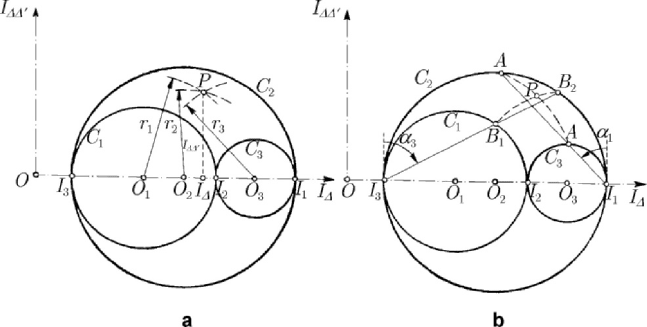
MECHANICAL SYSTEMS, CLASSICAL MODELS

152

the point

P of co-ordinates I

and I

ΔΔ

′

is the piercing point of these arcs of circle.

Figure 3.11. Mohr’s circles. Determination of the components of the moments of inertia

tensor for the direction n : analytical (a) and graphical (b) method.

One can use also a graphic method. Let be the tangents to the circle

, at the point

in which the latter one intersects the axis

and let us set up straight semi-lines

inclined by the angles

α and

α with respect to those tangents, respectively

(Fig.3.11,b); these semi-lines pierce the circles

and

at the points

A and

A ,

respectively, and the circles

and

at the points

and

, respectively. One can

easily prove that the arc of circle of radius

r and centre

passes through the points

A and

A , while the arc of circle of radius

r and centre

passes through the points

and

; their intersection is just the point

. The construction is thus completely

specified.

An important rôle is played by the approximation methods of computation of the

integrals, by the graphical methods, by the methods using apparatuses for graphical

determinations, by the experimental methods a.s.o.

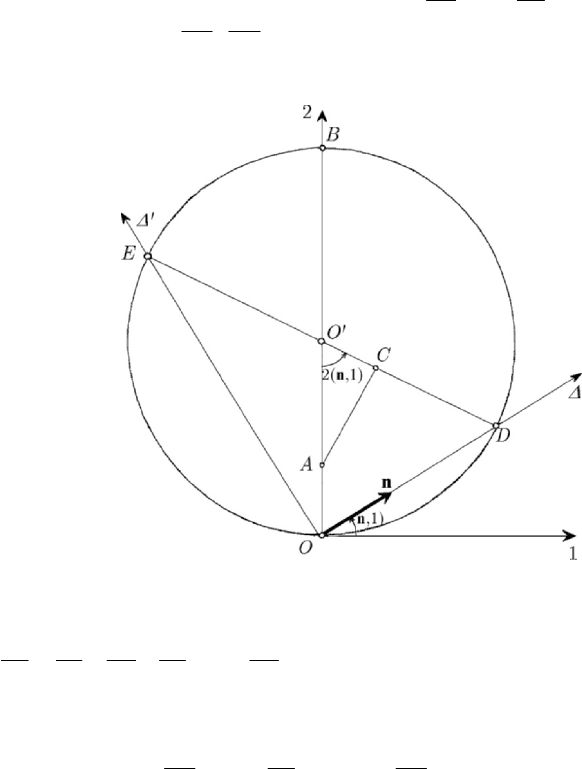
1.2.7 Two-dimensional geometric representations

We may represent the variation of the axial moments of inertia

and I

′

given by

(3.1.87) and (3.1.87'), respectively, by a rotation of the axes

1O , 2O about the point

O , as a function of the angle

(

)

,1n (Fig.3.12,a); the curve of fourth degree thus

obtained is symmetric with respect to the two principal axes of inertia. The moments of

inertia corresponding to the bisectrices of the angles formed by the principal axes of

inertia are also put into evidence.

As well, the variation of the centrifugal moment of inertia

ΔΔ

′

by the angle

(

)

,1n

is represented in Fig.3.12,b also by a curve of fourth degree, symmetric both with

respect to the principal axes of inertia and to the bisectrices of the angles formed by

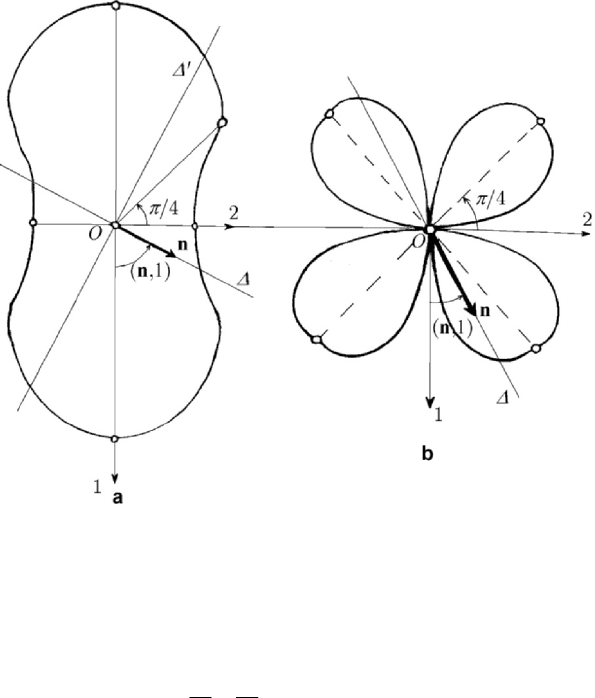
Mass geometry. Displacements. Constraints

153

those axes (with respect to which the considered moments of inertia have extreme

values).

If the geometric support

Ω is contained in the plane

Ox x , then the relations

(3.1.102) become

Figure 3.12. Variation of the axial (a) and centrifugal (b) moments of inertia.

222

11 22

Ia Ia K==

(3.1.108)

and one obtains the ellipse of inertia (

≤

)

= ;

(3.1.109)

hence, the principal moments of inertia are in inverse proportion to the squares of the

semiaxes of the ellipse of inertia. To the semi-minor axis of the ellipse corresponds the

maximal moment of inertia, while to the semi-major one corresponds the minimal

moment of inertia. If the two principal moments of inertia are equal (

II= ), the

ellipse of inertia is a circle (

), and any axis passing through the pole O is a

principal axis of inertia.

For instance, in the homogeneous case, we can take

/KIIA= , obtaining thus

ai= ,

ai= , so that the equation of the ellipse becomes (Fig.3.13)

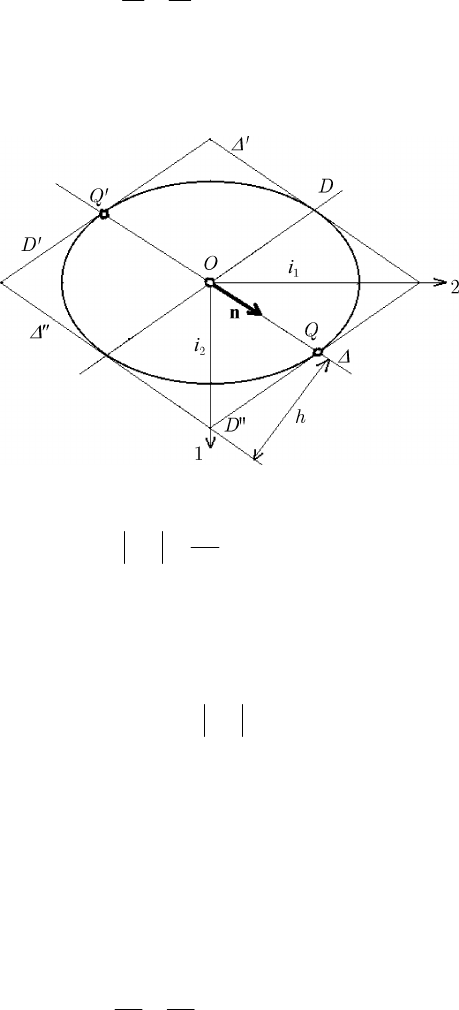
MECHANICAL SYSTEMS, CLASSICAL MODELS

154

(3.1.109')

We notice that we have

222

KAii= too; on the other hand, taking into account

(3.1.30') and (3.1.100), we obtain

Figure 3.13. Properties of the ellipse of inertia.

JJG

(3.1.110)

a remarkable relation, specifying the radius vector of the point

Q .

Let be

′

and Δ

′′

the tangents to the ellipse, parallel to the axis Δ , and D

′

and

′′

the tangents parallel to the axis

, at the points Q and

′

, respectively, Δ and

D being two conjugate diameters of the ellipse; one obtains thus a parallelogram, the

area of which is an invariant equal to

4hOQ

JJG

, h being the distance from the centre O

to one of the tangents

′

, Δ

′

. If the axis Δ coincides with one of the principal axes

of inertia, the parallelogram becomes a rectangle of area

4ii ; taking into account

(3.1.110), we get

, (3.1.110')

hence a graphical evaluation of the gyration radius with respect to an arbitrary axis

Δ .

Obviously, also in this case one can introduce an ellipse of gyration of the form

(analogous to (3.1.105))

′′

= .

(3.1.111)

Mass geometry. Displacements. Constraints

155

By eliminating the angle

(

)

,xn between one of the relations (3.1.87), (3.1.87') and

the relation (3.1.87''), we get

() ()

12 12 12

xx xx xx

III I II I

ΔΔ

′

⎡⎤⎡⎤

−+ += − +

⎢⎥⎢⎥

⎣⎦⎣⎦

(3.1.112)

Figure 3.14. Mohr’s circle. Principal axes and moments of inertia.

The relation remains valid if we replace

by I

′

. Taking the axial moments of

inertia

and I

′

along the axis

Ox and the centrifugal moment of inertia I

ΔΔ

′

along the axis

Ox , we notice that the equation (3.1.112) corresponds to a circle of

centre

(

)

(

)

/2,0

OI I

′

+ and radius

()

[]

12 12

xx xx

RII I=− + (Fig.3.14).

Supposing that

II> and

I > , we obtain the points

(

)

212

xxx

PI I and

(

)

112

xxx

PI I

′

− on the circle; indeed,

()

AO OA I I

′′ ′

==− and

OP OP R

′′′

==, the affirmation made above being thus justified.

We notice that

()

tan

AO P

′

−

′

Taking into account the relation (3.1.88), it results

()

2,AO P x

′

= n ; we find also that

()

,AB P x

′

= n (Fig.3.14). We are in the case in which

(

)

min

,/4x π<n ,

II> and

I > , so that, corresponding to the results of Subsec. 1.2.5, the

direction of the axis

2O is given by BP

′

; analogously, the direction of the axis 1O

corresponds to the straight line

PB .

MECHANICAL SYSTEMS, CLASSICAL MODELS

156

We see that

OB OO R I

′′

=−=,

OB OO R I

′

+=, so that the extremities of

the diameter

′

specify the magnitudes of the principal moments of inertia

II> ,

corresponding to the formulae (3.1.91).

This circle, called O.Mohr’s circle (initially introduced by Culmann and Rankine),

puts into evidence – in a concise way – the properties of extremum of the moments of

inertia with respect to axes rotating about a point.

By eliminating the angle

(

)

,1n between the relations (3.1.93) and (3.1.93''), one

obtains

() ()

12 12

III I II

ΔΔ

′

⎡⎤⎡⎤

−+ += −

⎢⎥⎢⎥

⎣⎦⎣⎦

(3.1.112')

Figure 3.15. Mohr’s circle. Determination of moments of inertia with

respect to two orthogonal axes.

The equation holds also if we replace

by I

′

. We get thus a circle of Mohr, drawn

with the aid of the principal moments of inertia, in the plane

12O , which allows us to

determine the axial moments of inertia

and I

′

, as well as the centrifugal moment

of inertia

ΔΔ

′

, corresponding to a given angle

(

)

,1n

(Fig.3.15). Starting from the

centre

(

)

(

)

/2,0OI I

′

+ of the circle of radius

(

)

/2RII

− and taking into

account the relations (3.1.93)-(3.1.93''), we find the points

(

)

,PI I

ΔΔ

′

and

(

)

,PI I

ΔΔΔ

′′

′

−

, II

′

> , 0I

ΔΔ

′

> , corresponding to the angle

(

)

2,1n

or to the

angle

(

)

,1n

, respectively; the searched moments of inertia are thus obtained. We

notice also that for

()

,1 /4π

n we get the extreme centrifugal moments of inertia,

which have the properties mentioned in Subsec. 1.2.5, corresponding to the points

and

′

on the circle.

Mass geometry. Displacements. Constraints

157

Another geometric construction was proposed by Mohr too and was improved by R.

Land; it is known as Land’s circle. As in the previous case, we suppose that the axial

moments of inertia

II< and the centrifugal moment of inertia

I are known.

Figure 3.16. Land’s circle. Principal axes and moments of inertia.

With respect to the frame of reference

Ox x

, we take the segments

OA I= and

AB I=

on the axis

Ox ; on OB as diameter, we construct a circle with the centre

(

)

(

)

0, /2

OII

′

+ , of radius

(

)

RI I

+ and tangent at O to the axis

Ox . We build up a segment AC , parallel to the axis

Ox , and having the same

direction, so as to have

AC I= (if

, then the point C must be in the

opposite direction); the straight line

′

pierces the circle at the points D and E

(Fig.3.16).

(

)

,xn is the angle formed by OD with the axis

Ox , then it follows that

()

2,OO D x

′

= n . We notice that

() ()

12 1 21

/2 /2

xx x xx

OA I I I I I

′

=+ −=− ,

hence

()

[]

21 12

xx xx

OC I I I

′

=− +

MECHANICAL SYSTEMS, CLASSICAL MODELS

158

Taking into account the formulae (3.1.91), we get

EC I

CD I

; on the other

hand,

()

12 2 1

tan 2 , / 2 /

xx x x

xACOAI II

′

== −n , so that OD is along the axis

2O , while OE is along the axis 1O .

Figure 3.17. Land’s circle. Determination of moments of inertia with

respect to two orthogonal axes.

With respect to the principal axes 1O , 2O , one can construct a circle of diameter

OB OA AB=+,

OA I= ,

AB I

and of radius

(

)

/2RII

+ , tangent to

1O at O (Fig.3.17). By means of the angle

(

)

,1n , we draw the straight lines OD and

OE along the axes Δ and Δ

′

(ΔΔ

′

⊥

), respectively; the points D and E are the

extremities of a diameter. The point

C is the foot of the normal from A to DE . It is

easy to verify that

DC I

′

= , CE I

= and AC I

ΔΔ

′

= , obtaining thus the axial

moments of inertia

, I

′

and the centrifugal moment of inertia I

ΔΔ

′

, corresponding

to the direction

(

)

,1n with respect to the principal axis 1O .

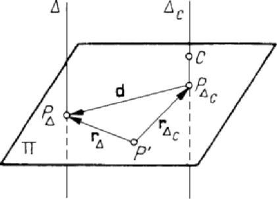
1.2.8 Huygens-Steiner theorems

Let be an axis

Δ and an axis

Δ , parallel to the first one and passing through the

centre of mass

C of the mechanical system. A point P of the system is projected at

′

on a plane Π , normal to both axes Δ and

Δ ; this plane is pierced by the axes at

the points

and

, respectively. Denoting PP

ΔΔ

′

JJJJG

r ,

ΔΔ

′

JJJJJG

r and

ΔΔ

JJJJJJG

d , and noting that we have to do with equipollent vectors, contained in the

plane

Π , we may write (Fig.3.18)

Mass geometry. Displacements. Constraints

159

(

)

222

ddd2dd

CCC

Irm mrm mdm

ΔΔ Δ Δ Δ

ΩΩ Ω Ω Ω

==+=+⋅+

∫∫ ∫ ∫ ∫

rd dr ;

observing that the static moment with respect to the centre of mass vanishes, we have

II Md

ΔΔ

(3.1.113)

Figure 3.18. Huygens-Steiner theorem.

and we can state

Theorem 3.1.4 (Huygens-Steiner). The moment of inertia of a mechanical system with

respect to an axis

Δ is equal to the sum of the moment of inertia of the same system

with respect to an axis

Δ parallel to the first one, passing through the centre of mass,

and the moment of inertia of the centre of mass, at which we consider concentrated the

mass of the whole mechanical system, with respect to the axis

Δ .

It follows that, being given all axes which have the same direction, the moment of

inertia of a mechanical system is minimal for that axis which passes through the centre

of mass. The moments of inertia with respect to the central axes (the axes which pass

through the centre of mass) are called central moments of inertia; the moments of

inertia which correspond to the central principal axes of inertia are called central

principal moments of inertia. Corresponding to what was related before, from all the

axes passing through the point

C , there exists one (or at least one if we have equal

moments of inertia) with respect to which the axial moment of inertia admits a

minimum minimorum. We notice also that the locus of the parallel axes which have the

same moment of inertia is a circular cylinder of radius

d , the axis of the cylinder

passing through

C ; as well, the variation of the moments of inertia with respect to axes

of the same direction may be represented by a paraboloid of rotation, the axis of which

has the same direction and passes through

C .

Let

′

be another axis, parallel to the axis Δ ; if we write a formula of the form

(3.1.113) for this axis too, and if we subtract the two formulae, then we get

(

)

IIMdd

′

=+ −

;

(3.1.114)

this result allows us to pass from an axis of a given direction to an axis parallel to the

latter one, taking into account the distances

d and d

′

from these axes to an axis which

has the same direction and passes through

C .