Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

120

hence, the axial static moment of a plane mechanical system with respect to an axis

contained in the plane of the system is equal to the static moment of the centre of mass,

at which one considers concentrated the mass of the whole mechanical system, with

respect to the very same axis. We can state also that the centre of mass of a plane

mechanical system is characterized by the vanishing of the axial static moment with

respect to an axis contained in the plane and passing through it.

In the case of a linear mechanical system (the geometric support

Ω of which is a

straight line), one has to do only with the polar static moment (with only one

component) with respect to a pole belonging to the straight line.

1.1.3 Properties. Applications

We notice that the centre of mass is placed in the interior of any convex closed

surface

Σ which contains in its interior the geometric support Ω of the considered

mechanical system. Indeed, taking the plane of co-ordinates

Ox x tangent to the

surface

Σ at an arbitrary point of it, taken as pole O , and admitting the direction of the

axis

Ox towards the interior of Σ , it follows that for all the points of the geometric

support

Ω we have ≥

0x ; the formula (3.1.1') allows us to affirm that ≥

0ρ (the

equality takes place if

Ω is a plane geometric support). Hence, the centre C is situated

in the same part of the considered plane as the surface

Σ ; because ∈O Σ is

arbitrarily chosen, it follows that the centre

C is situated in the interior of the surface

Σ .

If the support

Ω is a straight line or a plane, then the centre C is on the straight line

or is contained in the plane. In the first case, if we choose this line as the

Ox –axis,

then we find easily that

0ρρ ; in the second case we choose the respective

plane as plane

Ox x and obtain

0ρ .

If the mechanical system admits a plane of geometric (the geometric support

Ω

admits a plane of symmetry) and mechanical (the symmetric points of the geometric

support

Ω have the same unit mass, in the case of a continuous mechanical system, or

the same finite mass, in the case of a discrete mechanical system) symmetry, then we

take this plane as plane

Ox x ; applying the formula (3.1.1'), we notice that some

points of the support

Ω belong to the plane

0x , while the other points are pairs of

symmetric points, obtaining thus

0ρ . The centre of mass belongs thus to the plane

of symmetry. If there exist two (or three) planes of geometric and mechanical

symmetry, then the centre

C belongs to the straight line (centre) of intersection of these

planes, which – obviously – will be an axis (a centre) of geometric and mechanical

symmetry. If the mechanical system admits a plane

Π diametrically conjugate from

geometric and mechanical point of view to a direction

Δ (to each point

P of the

mechanical system there corresponds a point

P of the same system, having the same

mass, so that the segment

PP has the direction of Δ and the middle in the plane

then the point

C will belong to the plane Π ; in particular, if

⊥

ΔΠ, then this plane

is a plane of geometric and mechanical symmetry.

Mass geometry. Displacements. Constraints

121

For any division

S ,

1,2,...,in, of the mechanical system S in n disjoint

subsystems,

∑

SS,

we may write (see Theorem 3.1.1)

∑

ρ ,

(3.1.11)

where

and

ρ are the mass and the position vector of the centre of mass

respectively, corresponding to the subsystem

S , and

and

are the mass and the

position vector of the centre of mass

, respectively, corresponding to the given

mechanical system

S ; by means of the formulae of definition and the property of

associativity (additivity) of the finite sum (of the integral), the proof is obvious. If a

mechanical system

S may be considered as resulting by taking off a mechanical system

S from a mechanical system

S , then the formula (3.1.11) allows us to write

11 22

−

(3.1.12)

the notations being analogous to the above ones.

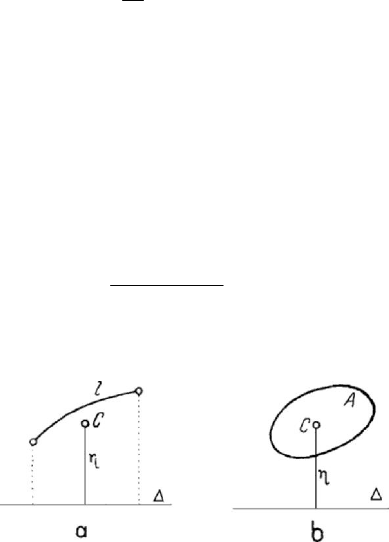
Figure 3.2. Pappus-Guldin theorems: for a surface (a) and for a volume (b).

The notion of centre of gravity allows us to state

Theorem 3.1.2 (Pappus-Guldin). Let be an arc of a rectifiable plane curve of length l ,

coplanar with an axis

Δ , at the same part of this one, which rotates by an angle

≤ 2απ about the axis; the area of the surface thus obtained is given by

Slαη

, (3.1.13)

where

η is the distance from the centre of gravity C of the arc of curve to the axis

(Fig.3.2,a).

In the particular case of a surface of rotation (

2απ), we obtain

2Slπη

, (3.1.13')

MECHANICAL SYSTEMS, CLASSICAL MODELS

122

where the product of the perimeter of the circle described by the point

C by the length

l is put into evidence. We may also state

Theorem 3.1.3 (Pappus-Guldin). Let be a plane figure of area A , coplanar with an

axis

Δ , at the same part of the latter one, which rotates by an angle ≤ 2απ about the

axis; the volume of the domain thus generated is given by

VAαη

(3.1.14)

where

η is the distance from the centre of gravity C of the plane figure to the axis Δ

(Fig.3.2,b).

In particular, in the case of a body of rotation (

2απ), we can write

2VAπη

(3.1.14')

where the product of the perimeter of the circle described by the point

by the area

A is put into evidence.

The proof of these theorems is obvious if one takes into account the definition and

the properties of the Riemann integral.

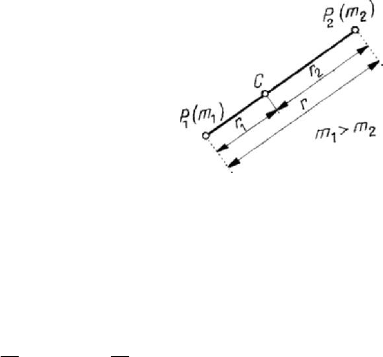
Figure 3.3. Centre of mass of a system of two particles.

For a discrete mechanical system, formed by two particles

P and

P , of masses

and

m , respectively, the centre of mass is on the segment

PP , at the distances

and

r from the extremities of it, so that (Fig.3.3)

rr r

+ ,

mm m

+ ,

mm≥ ;

(3.1.15)

we notice that the centre

C is closer to the particle of the greatest mass (in the

considered case, closer to the particle

P ).

Taking into account the properties mentioned above, one observes easily that the

centre of gravity of a discrete mechanical system formed by three particles of equal

masses, or of a triangular line (or figure) is at the piercing point of its median lines; if

the three masses are not equal, one obtains the famous theorem enounced in 1678 by

Giovanni Ceva.

The centre of gravity of a contour (or figure) in form of a parallelogram (in

particular, rectangle) is at the piercing point of its diagonals, the centre of gravity of a

Mass geometry. Displacements. Constraints

123

contour (or figure) having a circular form is at its centre a.s.o. Analogously, the centre

of gravity of a discrete mechanical system formed by four non-coplanar particles of

equal masses, or of a trihedral surface (or domain) is the piercing point of its median

lines. Obviously, we can admit that all these lines, figures and domains correspond to

homogeneous bodies.

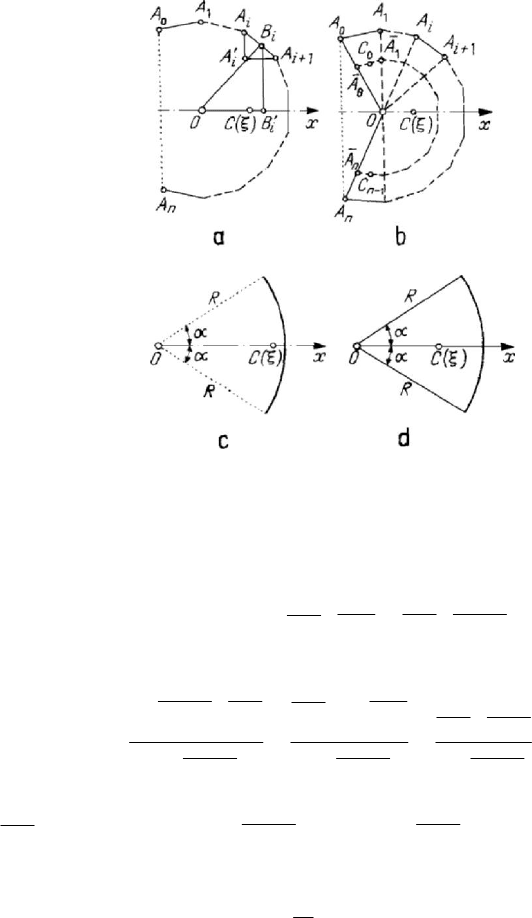
Figure 3.4. Centre of gravity of a regular polygonal line (a) or sector (b).

Centre of gravity of an arc (c) or sector (d) of circle.

In the case of a regular polygonal line

...

AA A , formed by n segments of length

, the centre of gravity is on the symmetry axis, which passes through a vertex (n

even) or through the middle of a segment (

n odd). The similar triangles

′

AA A and

′

OB B (Fig.3.4,a) allow us to write

′′

⋅=⋅

iii ii

OB A A OB A A

, so that the centre of

gravity is given by

000

111

000

iiiii

iii

nnn

iii

A A OB OB A A

OB A A

AA AA AA

−−

−−−

+++

===

′′

⋅⋅

⋅

===

∑∑

∑∑∑

;

OB a is the short radius,

AA l the side,

AA c

the chord and =pnl

the perimeter, then we can write

ξ =

(3.1.16)

MECHANICAL SYSTEMS, CLASSICAL MODELS

124

The centre of gravity of the polygonal sector

...

AA A (Fig.3.4,b), formed by the

triangles

OA A ,

=−0,1,2,..., 1in

, coincides with the centre of gravity of the

polygonal line

...

AA A

, which passes through the centres of gravity

−

12 1

, , ,...,

CCC C

of the n triangles; in this case, it is obvious that

ξ =

(3.1.17)

In the case of an arc of circle of angle

≤

22απ and of radius R (Fig.3.4,c) we

obtain, by a process of passing to the limit (

2pRα ,

2sincRα , =aR),

sinc

== ;

(3.1.16')

as well, for a circular sector of angle

≤

22απ and radius R (Fig.3.4,d) we write

22sin

== .

(3.1.17')

In particular, for a semicircular line (

/2απ ) it results

Rξ

= ,

(3.1.16'')

while for the figure in form of a semicircle we obtain

Rξ

= .

(3.1.17'')

Analogous considerations can be made for three-dimensional bodies; for example, in

the case of a homogeneous semisphere of radius

R we have

Rξ = .

(3.1.18)

Let be a compound figure formed by two adjoining rectangles (Fig.3.5). We obtain

thus the centres

C and

C ; the centre C of the compound figure is on the segment

CC , its position being determined by formulae of the form (3.1.15), where the

masses, considered concentrated at those centres, are proportional to the areas of the

component rectangles. Dividing the compound figure in other two rectangles, we are led to

the centres

′

C and

′

C ; the centre C will belong to the segment

′

CC , hence it is at

the piercing point of this segment with the segment

CC . Thus, the formula (3.1.11)

leads to a graphic construction of the geometric centre of gravity

C . We notice that the

above-considered figure may also be obtained by taking off a rectangle from another

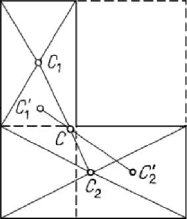
Mass geometry. Displacements. Constraints

125

one, applying thus the formula (3.1.12); obviously, a graphic construction can be used

too.

Figure 3.5. Centre of gravity of a compound figure formed by two adjoining rectangles.

1.2 Moments of inertia

In mechanics and physics can appear moments of the form

123

dxxx m

ααα

Ω

∫

123

,, 0ααα≥

(3.1.19)

of order

123

αα α α

, where the mass

r()mm is a distribution and we have

introduced the Stieltjes integral. In the case

===

123

0αααα one obtains the

mass

M , while the case

α ,

= 0

αα ,

≠

≠≠ijki

=,, 1,2,3ijk

= 1α corresponds to a planar static moment. The moments for which > 2α are not

of a particular interest. In what follows, we will deal with moments of second order

(

= 2α ), called moments of inertia, which play an important rôle in the dynamics of

mechanical systems. We mention also some considerations concerning tensors of nth

order and, in particular, tensors of second order, useful in the study of the moment of

inertia tensor.

1.2.1 Definitions. Properties

Let

S be a mechanical system of geometric support Ω . We define the polar

moment of inertia with respect to the pole

Irm

Ω

∫

(3.1.20)

the axial moments of inertia

(

)

Ixxm

Ω

∫

, jkl j

≠

≠≠,

,, 1,2,3jkl ,

(3.1.21)

and the planar moments of inertia

Ol Ox x l

II xm

Ω

∫

, jklj

≠

≠≠,

,, 1,2,3jkl ,

(3.1.22)

MECHANICAL SYSTEMS, CLASSICAL MODELS

126

where we have introduced the Stieltjes integral,

()mm

r being a distribution.

In the case of a discrete mechanical system of particles of finite masses

m ,

1,2,...,in=

, we may write

Imr

∑

(3.1.20')

()

Imx x

⎡⎤

⎣⎦

∑

, jklj

≠

≠≠,

,, 1,2,3jkl ,

(3.1.21')

()

Ox x

Imx

∑

jklj

≠

≠≠

,, 1,2,3jkl

(3.1.22')

while, in the case of a continuous mechanical system for which the geometric support

Ω occupies the volume V , there result

()d

IrVμ=

∫

r ,

(3.1.20'')

(

)

()d

IxxVμ=+

∫

r , jklj

≠

≠≠,

,, 1,2,3jkl ,

(3.1.21'')

()d

Ox x l

IxVμ=

∫

r ,

jklj

≠

≠≠

,, 1,2,3jkl

(3.1.22'')

To a homogeneous continuous mechanical system there correspond the geometric

moments of inertia (for the sake of simplicity, we use the same notation)

IrV=

∫

(3.1.20''')

(

)

IxxV=+

∫

jklj

≠

≠≠

,, 1,2,3jkl

(3.1.21''')

Ox x l

IxV=

∫

, jklj

≠

≠≠,

,, 1,2,3jkl ,

(3.1.22''')

while for a homogeneous discrete mechanical system we can write

∑

(3.1.20

)

()

Ixx

⎡⎤

⎣⎦

∑

, jklj

≠

≠≠,

,, 1,2,3jkl ,

(3.1.21

)

()

Ox x

∑

, jklj

≠

≠≠,

,, 1,2,3jkl .

(3.1.22

)

The above moments of inertia verify the relations

()

123

23 31 12

xxx

OOxx Oxx Oxx

II I I III=++=++,

(3.1.23)

lkl

Ox x Ox x

II I=+,

OOxx

II I

+ , jklj

≠

≠≠,

,, 1,2,3jkl , (3.1.23')

Mass geometry. Displacements. Constraints

127

from which

()

xxx

Ox x

IIII=+−, jkl j

≠

≠≠,

,, 1,2,3jkl ;

(3.1.23'')

hence, the polar moment of inertia and the planar moments of inertia can be expressed

by means of the axial moments of inertia, so that it is sufficient to consider the latter

ones. All these moments of inertia are non-negative.

We are led to the relations

kl k

xx xxx

II III−≤≤+,

II≥ , jklj

≠

≠≠,

,, 1,2,3jkl , (3.1.24)

of the type of the triangle relations; the equalities take place if the geometric support

Ω

is contained in a manifold of the three-dimensional space (a plane or a straight line).

Π ,

Π and

Π are two by two orthogonal planes, then we can write, in general,

II I

ΠΠ

=+,

ΔΠ Π≡∩,

123

II I I

ΠΠΠ

++,

123

O ΠΠΠ

≡

∩∩

(3.1.25)

Δ is an axis of geometric and mechanical symmetry, then the moments of inertia

with respect to any plane

Π passing through Δ are equal; taking into account the first

relation (3.1.25), we obtain

2II

. (3.1.26)

is a centre of geometric and mechanical symmetry, then the moments of inertia

with respect to any plane

passing through

are equal; the second relation (3.1.25)

and the relation (3.1.26) lead to

II I

==,

(3.1.26')

where

Δ is a straight line passing through

. For instance, in the case of a

homogeneous whole sphere of radius

R and mass

, we can write

IMR= ,

IMR

= ,

IMR

= .

(3.1.27)

We introduce the centrifugal moments of inertia (products of inertia)

Ixxm

Ω

∫

≠

,1,2,3jk

(3.1.28)

too, which may be of the form

MECHANICAL SYSTEMS, CLASSICAL MODELS

128

() ()

Imxx

∑

, ()d

IxxVμ=

∫

r ,

≠

,1,2,3jk

(3.1.28')

or of the form

() ()

Ixx

∑

, d

IxxV=

∫

, jk

≠

, ,1,2,3jk

;

(3.1.28'')

these moments of inertia can be also negative. We notice that

()()

()

jj j

kkkjkjk

xx x x x x d d

⎡⎤

′

=+−−=−

⎣⎦

, jk

≠

, ,1,2,3jk= ,

where

d ,

′

are the distances of a point of the mechanical system to the bisector

planes

Π ,

′

of the dihedron formed by the planes 0

, respectively;

we obtain

()()

jk jk

IIIII

ΠΔ

′′

=−=−, jk

≠

, ,1,2,3jk

(3.1.29)

where

Δ ,

′

are the bisectrices of the angle formed by the axes

Ox ,

respectively, and we used formulae of the form (3.1.23'').

If the plane

Ox x is a plane of geometric and mechanical symmetry, (the points of

co-ordinates

x and

x− of the mechanical system have the same contribution in the

computation of the integrals of the form (3.1.28)) or if the axis

Ox is an axis of

geometric and mechanical symmetry, then we obtain

lkl

xx xx

II==,

jklj≠≠≠, ,, 1,2,3jkl= .

The gyration radius (radius of inertia) with respect to the axis

Δ is defined by the

relation

(3.1.30)

and represents the distance of a material point at which is concentrated the mass

the whole mechanical system to the axis

Δ ; in the case of a geometric moment of

inertia of a homogeneous mechanical system of volume

, we may write

= .

(3.1.30')

If the geometric support

Ω

is contained in the plane

Ox x

, then we may define the

polar moment of inertia

(

)

222

Irmxxm

ΩΩ

==+

∫∫

(3.1.31)

Mass geometry. Displacements. Constraints

129

the axial moments of inertia

Ixm

Ω

∫

αβ

≠

,1,2αβ

(3.1.32)

and the products of inertia

Ixxm

Ω

∫

;

(3.1.33)

for discrete or continuous mechanical systems one can put in evidence analogous

formulae. We notice the relation

III

+ . (3.1.34)

If the geometric support

Ω

is a circle, of centre

and radius R , then we obtain (for a

homogeneous mechanical system)

= ,

II R

== .

(3.1.34')

In the case of an axis or of a centre of geometric and mechanical symmetry,

respectively, one can emphasize properties analogous to those mentioned in the three-

dimensional case. If the geometric support

Ω is on a straight line, then one can define

only polar moments of inertia (in the one-dimensional space).

1.2.2 Tensors of nth order

We will deal with some elements of tensor algebra and analysis, considering scalars,

tensors of first order as well as of nth order, and we will put into evidence various

particular cases; we will consider only tensors in

E .

One can pass from a positive orthonormed basis

B of unit vectors

i to another

positive orthonormed basis

B ' of unit vectors

′

i by means of formulae (2.1.8)-

(2.1.11), given at Chap. 2, Subsec. 1.1.2.

The cosines

α which are introduced verify the relations

ik jk

αα δ= ,

ki jk

αα δ

, ,1,2,3jk

. (3.1.35)

As well, one can pass from a system of co-ordinate axes to another one by means of the

formulae (2.1.11) or of the formulae

′

∂

′

∂

,1,2,3kj

(3.1.36)

Let be a function

(

)

123

,,UUxxx= ; by a change of co-ordinates of the form

(2.1.11), we obtain the function

(

)

123

,,UUxxx

′

′′′′

. If the condition