Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

110

() ( )

δ=−Qr F r r ,

1,2,...,in

(2.2.43)

By means of the resultant (2.2.38'), applied at the same point

P , we may write the

volume density in the form

() () ( )

==−

∑

Qr Q r R r r

;

(2.2.43')

the properties of the concentrated forces applied at the same point are thus preserved in

this representation.

In the case of concentrated forces represented by bound vectors, at different points of

application, one cannot speak – in general – about their composition. However, in some

cases, we can give a representation in distributions of a system formed by two such

concentrated forces. So, in the case of a system of

2n > concentrated forces, applied

at different points, one can try their composition if they are parallel; otherwise, one can

decompose each force along three directions, and one obtains three systems of

parallel forces (components of the forces initially given).

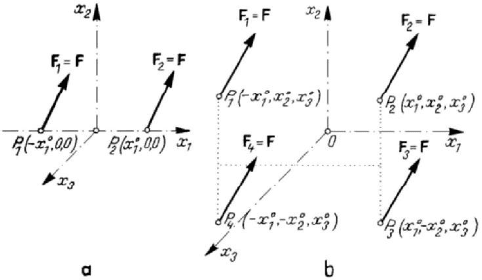
Figure 2.20. System of two (a) or four (b) parallel concentrated forces

of the same modulus and direction.

Let be, for instance, two parallel forces of the same direction and the same intensity

(

==FFF, as free vectors), applied at the points

(

)

,0,0Px− and

()

,0,0Px ,

0x >

, respectively (Fig.2.20,a); there correspond the equivalent vector fields

()

(

)

1 123 1 1 23

,, ,,xxx x x xxδ=+QF ,

()

(

)

2123 1 123

,, ,,xxx x x xxδ=−QF

The volume density of this system of two forces is given by

()

(

)

020

123 1 1 1 23

,, 2 ,,xxx x x x xxδ=−QF ,

0x > ,

(2.2.44)

where we took into account the relation (1.1.40'); this relation can be used as a rule for

the composition of the two equipollent forces (equal as free vectors), applied on the

Mechanics of the systems of forces

111

-axis. We have taken

as axis

, but this is not essential for the problem;

e.g., for the points of application

(

)

1123

,,Pxxx

′

and

(

)

2123

,,Pxxx

′′

we obtain

() ()()

(

)

123 1 1 1 1 1 1 2 2 3 3

,, , ,xxx x x x x x x x x x xδ

′′′ ′ ′′

=− − − − −QF ,

(2.2.44')

corresponding to the relation (1.1.41).

Let be also a system of four parallel forces having the same direction and the same

intensity (

1234

====FFFFF, as free vectors), applied at the points

()

000

1 123

,,Pxxx− ,

()

000

2123

,,Pxxx ,

(

)

000

31 23

,,Px xx− ,

(

)

000

4123

,,Pxxx−− ,

,0xx> ,

respectively (Fig.2.20,b). The equivalent vector field is given by

()

(

)

[

000

123 1 1 2 2 3 3

,, , ,xxx x x x xx xδ=+−−QF

(

)

(

)

000 000

112233 112233

,, ,,xxxxxx xxxxxxδδ+− − −+ − + −

()

]

000

112233

,,xxxxxxδ++ + −;

using the relation (1.1.42), we obtain the composition formula

()

() ()

(

)

00 2 0 2 0 0

123 12 1 1 2 2 3 3

,, 4 , ,xxx xx x xx xxxδ=−−−QF ,

,0xx> .

(2.2.45)

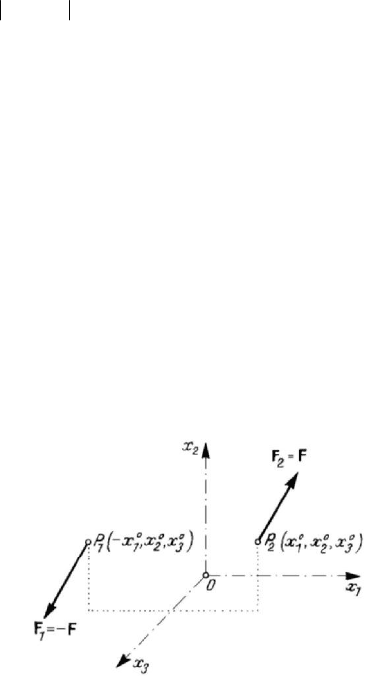
Figure 2.21. System of two parallel forces of the same modulus and opposite directions.

Let us consider also two parallel forces of opposite directions, but of the same

intensity (

=− =FFF, as free vectors), applied at the points

(

)

000

1 123

,,Pxxx− and

()

000

2123

,,Pxxx ,

0x > , respectively (Fig.2.21). The equivalent vector field is

()

(

)

[

]

000 000

123 1 12 23 3 1 12 23 3

,, ,, ,,xxx x xx xx x x xx xx xδδ=− + − − + − − −QF ;

using the relation (1.1.43), we may write

()

(

)

20 0 0

123 1 1 1 2 2 3 3

,, 2 , ,xxx x x x x x x xδ=−−−QF ,

(2.2.46)

obtaining thus the searched composition formula.

MECHANICAL SYSTEMS, CLASSICAL MODELS

112

In the case of deformable continuous media there appear various concentrated loads

(mechanical quantities which have a punctual support), which play an important rôle,

for instance: directed concentrated moments and dipoles of concentrated forces of

various orders, centres of rotation, centres of plane or spatial dilatation etc.; all these

loads can be expressed by means of distributions, starting from the representation

(2.2.42), corresponding to a concentrated force.

One can show that a linear load of the form

(), [,],

()

0 , [ , ],

uuab

uab

∈

⎧

⎪

⎨

∉

⎪

⎩

(2.2.47)

the support of which is a curve of parametric equations (

()u

rr )

()

xfu

∞

∈ ,

1, 2, 3i

, lim () ()

uf u

→±∞

∞ ,

(2.2.47')

leads to a volume density

() ()

123 123

123

, , , , () () ()d

xxx xxx u fufu u

xxx

∞

−∞

∂

′′

∂∂∂

∫

QF,

(2.2.47'')

where

() d()/d

ufuu

′

, while

()

(

)

(

)

123 1 1 2 2 3 3

, , () () ()

xxx x fu x fu x fuθθθθ=− − −

11 22 33

1, ( ), 1, 2, 3, [ , ],

0, () or () or () or [,],

xfui uab

xfuxfuxfuuab

≥=∈

⎧

⎪

⎨

<<<∉

⎪

⎩

(2.2.47''')

being Heaviside’s function.

As well, in the case of a superficial load, given by the relation

()

(

)

(

)

()

,, , ,

0 , , ,

uv uv D

uv D

∈

⎧

⎪

⎨

∉

⎪

⎩

(2.2.48)

where

D is the definition domain of the parameters u and v , and the support of which

is the surface of parametric equations (

(,)uv

rr )

()

xfuv= ,

∞

∈ , 1, 2, 3i

(

)

(

)

lim , ,

uv f uv

+→∞

∞ ,

(2.2.48')

we are led to the volume density

() ()

123 123

123

,, ,,

xxx xxx

xxx

∞∞

−∞ −∞

∂

∂∂∂

∫∫

()()() ()

,,, ,dduv E uv G uv F uv u v×−F ,

(2.2.48'')

Mechanics of the systems of forces

113

where

()

(

)

()

(

)

123 1 1 2 2 3 3

,, , , ,

xxx xfuvxfuvxfuvθθθθ=− − − ,

(2.2.48''')

being Heaviside’s function, and where we have used the differential parameters

()

(

)

()

()()

()

Euv

uuu

Fuv

uvuv

Guv

vvv

∂∂

∂

⎧

⎪

∂∂∂

⎪

∂

∂∂

⎪

=⋅=

⎨

∂

∂∂∂

⎪

∂∂

∂

⎪

∂∂∂

⎩

(2.2.48

)

corresponding to the first basic form of the surface (4.1.15), (4.1.15').

The functions

()uF and

()

,uvF considered above are piecewise continuous and

lead to regular distributions.

The methods of the theory of distributions allow us to represent continuous loads, as

well as discontinuous ones, from a spatial point of view; we obtain also the

representation of concentrated loads. One can consider continuous and discontinuous

phenomena from a temporal point of view too; thus, the forces appearing in a

phenomenon which takes place in a very short interval of time (for instance, the

collision of two spheres) can be represented by Dirac’s distribution with respect to time.

Returning to a unitary representation in distributions (corresponding to the formula

(1.1.73)), we may write, in general,

Ω

∫

Rf , d

Ω

=×

∫

Mrf ,

(2.2.49)

where

Ω is the geometric support of the mechanical system S, while the integrals are

Stieltjes integrals. In the case of a discrete mechanical system, we find again the

formulae (2.2.38), (2.2.38'), while for a continuous one we obtain formulae (2.2.39),

(2.2.39'), and the integrals become Riemann integrals.

In the case of a deformable mechanical system (the forces are modelled by bound

vectors), the torsor (2.2.38), (2.2.38') leads to necessary conditions which can occur in

various problems (relations of equivalence, equivalence to zero etc.); in the case of a

non-deformable mechanical system (the forces are modelled by sliding vectors), the

torsor leads to conditions which are also sufficient for the respective problems.

We have seen in Chap. 1, Subsec. 1.1.11 that the forces acting upon a mechanical

system can be external forces or internal forces, the latter ones being always pairs (they

are applied at the points

P and

P ), being linked axiomatically by the relation

(1.1.81). Taking into account the results of Subsec. 2.1.1, we may affirm that the

moment with respect to an arbitrary pole of such a pair of internal forces vanishes, the

mechanical system being deformable or even non-deformable; hence, the torsor of these

forces with respect to the pole

O (Fig.1.18) is equal to zero

{

}

ij ji

=FF 0.

(2.2.50)

MECHANICAL SYSTEMS, CLASSICAL MODELS

114

We can make an analogous affirmation for the whole system of internal forces acting

upon the given mechanical system. If the relation (2.2.50) holds, then we have

{} ( )

ij ji i ij j ji j i ji i j ji

PP=×+×=−×= ×=





MFF rF r F r r F F 0

;

hence,

ij i j ij

PPλλ==





Fr, λ scalar, and the considered forces are a pair of internal

forces.

A pair of internal forces constitutes a finite dipole of forces, which can be

represented, in distributions, by a formula of the form (2.2.46).

By decomposing a mechanical system in two subsystems, some forces which – at the

beginning – have been internal forces, may become external ones; hence, the

classification of the forces in internal and external ones is conventional.

The forces acting upon mechanical systems are modelled with the aid of vectors;

these ones will thus play an important rôle to determine the class of equivalent systems

of forces, which lead to the same effects of mechanical order.

Chapter 3

MASS GEOMETRY. DISPLACEMENTS.

CONSTRAINTS

It is necessary to introduce some notions which play an important rôle in a static and

dynamic study of mechanical systems; we will thus consider problems of mass

geometry, as well as problems concerning displacements and constraints, expressed by

means of the latter ones.

1. Mass geometry

Mass plays an important rôle in the dynamics of mechanical systems; we are thus led

to the study of moments of first order (static moments) or of second order (moments of

inertia).

1.1 Centres of mass

We introduce, in what follows, the notions of centre of mass, centre of gravity and

static moment (moment of first order); we give also some properties useful for the

practical computation.

1.1.1 Centres of mass. Centres of gravity

Let

S be a mechanical system of geometric support Ω . We call centre of mass of

this system a point

C , which may not belong to it, defined by the position vector

Ω

∫

rρ ,

(3.1.1)

the integral being a Stieltjes one, and the mass

()mm

r a distribution. Introducing

the density (1.1.71), (1.1.71''), we can write

∑

rρ ,

(3.1.2)

in the case of a discrete mechanical system of

n particles

, of position vectors

and masses

m , 1,2,...,in= , or

115

MECHANICAL SYSTEMS, CLASSICAL MODELS

116

()d

μ=

∫

rrρ ,

(3.1.3)

in the case of a continuous mechanical system of density

()μ r . If the continuum is

homogeneous, it results

∫

rρ .

(3.1.4)

In components, we may write

Ω

ρ =

∫

1, 2, 3j ,

(3.1.1')

as well as

()

∑

ρ ,

1, 2, 3j

(3.1.2')

()d

ρμ=

∫

r ,

1, 2, 3j

(3.1.3')

and

ρ =

∫

1, 2, 3j

(3.1.4')

In the case of a two-dimensional mechanical system, we replace the volume integral by

a surface one, using a superficial density; if the mechanical system is plane, then the

integral is a double one. As well, in the case of a one-dimensional mechanical system,

we replace the volume integral by a curvilinear one, introducing a linear density.

Figure 3.1. Centre of gravity of a heavy discrete mechanical system.

Let us admit that the mechanical system S, supposed to be non-deformable at a given

moment, is subjected to the action of a uniform gravitational field (for instance, the

Mass geometry. Displacements. Constraints

117

terrestrial gravitational field). To fix the ideas, we consider a discrete mechanical

system, the particles of masses

m being acted upon by the gravity forces

m , 1,2,...,in

, (3.1.5)

which form a field of parallel forces of the same direction. The system of particles

being non-deformable at a certain moment, the forces form a system of sliding vectors;

the central axis will pass through the point

C of position vector (Fig.3.1)

∑

ρ ,

given by the formula (2.2.36). We rotate the whole discrete mechanical system by a

given angle; the forces

G will not change their supports and their direction. This is

equivalent to the supposition that the system did not rotate, but the parallel forces did

rotate with the same angle; with the aid of a property put in evidence in Chap. 2,

Subsec. 2.2.7, it follows that the central axis passes through the same point

C . This

point will be called the centre of gravity of the mechanical system at a given moment, at

which the system is considered non-deformable; in the case of a uniform gravitational

field, it coincides with the centre of mass of the very same system. In the case of a

continuous mechanical system, one can make analogous considerations. If the

mechanical system is non-deformable, then the “instantaneous” centre of gravity

becomes “permanent”.

In general, in the case of a non-uniform gravitational field, the centre of gravity of a

mechanical system is the point of application of the resultant of the gravity forces acting

upon the points of this system (if the resultant moment vanishes, and this point of

application is independent of the position of the mechanical system; for instance, a

mechanical system with central symmetry in a gravitational field with axial symmetry).

We notice that the centre of mass has a more general significance, the centre of

gravity being put in evidence only in the presence of a gravitational field (for example,

the gravitational field of the Earth). The centre of gravity of a non-deformable

mechanical system is the same in any place on the surface of the Earth, because it

coincides with the centre of mass. The point

C is called also centre of inertia if we take

in consideration the inertial property of the mass. In the case of a non-deformable

mechanical system, the centre of mass

C is a point rigidly linked to this system (the

distance from

C to any point of the system is constant in time).

In the case of a homogeneous continuous mechanical system, the centre of gravity is

given by the relation (3.1.4); we are led thus to the notion of geometric centre of gravity

(which has a purely geometric character). Analogously, in the case of a discrete

mechanical system for which all the particles

P have the same mass, the centre of

gravity

C is specified by the position vector

∑

(3.1.2'')

MECHANICAL SYSTEMS, CLASSICAL MODELS

118

corresponding to the formula (3.1.2); this point is called also the barycentre of the

system of points

P .

Because the position of the centre of a system of parallel vectors does not depend on

the frame of reference used, it follows that the centre of gravity represents an intrinsic

characteristic of the considered mechanical system, the centre of mass having the same

property.

1.1.2 Static moments

We define the polar static moment of the mechanical system

S, of geometric support

Ω , with respect to the pole O in the form

Ω

∫

Sr,

(3.1.6)

where we have introduced a Stieltjes integral, the mass

r()mm being a distribution;

its components are the planar static moments (with respect to the planes of co-

ordinates)

Oj Ox x

SS xm

Ω

∫

≠

≠≠jklj,

,, 1,2,3jkl .

(3.1.6')

In the case of a discrete mechanical system, considered at the previous subsection, we

can write

∑

Sr,

()

Oj Ox x

SS mx

∑

, jklj

≠

≠≠,

,, 1,2,3jkl ,

(3.1.7)

and in the case of a continuous mechanical system we have

()d

Vμ=

∫

Srr, ()d

Oj Ox x

SS x V

Ω

μ==

∫

r ,

jklj

≠

≠≠

=,, 1,2,3jkl

;

(3.1.7')

to a homogeneous continuous mechanical system will correspond the geometric static

moment

∫

Sr, d

Oj Ox x

SS xV

Ω

∫

, jklj

≠

≠≠,

,, 1,2,3jkl ,

(3.1.8)

while for a homogeneous discrete mechanical system we obtain

∑

Sr,

()

Oj Ox x

SS x

∑

≠

≠≠jklj,

,, 1,2,3jkl .

(3.1.8')

Taking into account the relation of definition (3.1.1), one observes easily that

(3.1.9)

Mass geometry. Displacements. Constraints

119

SMρ

1, 2, 3j

; (3.1.9')

hence, we state

Theorem 3.1.1. The polar (planar) static moment of a mechanical system with respect

to a pole (plane) is equal to the static moment of the centre of mass, at which is

considered to be concentrated the mass of the whole mechanical system, with respect to

the same pole (plane).

The relations (3.1.9), (3.1.9') show that, in a certain manner, the centre of mass can

replace the whole given mechanical system; this observation holds also for other

mechanical quantities which we will define, the usefulness of the centre of mass

introduced above being thus put into evidence. If the pole

O (a plane) coincides with

(passes through) the centre of mass (

ρ ,

1, 2, 3j

), then the polar

(planar) static moment with respect to this pole (plane) vanishes and reciprocally.

Hence, the centre of mass of a mechanical system is characterized by the vanishing of

the polar (planar) static moment with respect to it (to a plane passing through it); one

can thus affirm once more that the centre of mass constitutes an intrinsic characteristic

of the considered mechanical system (there is only one point

C defined by the relation

(3.1.1)).

We notice that we can write the relation (3.1.9) also in the form

() ( )

OOC

SSSS,

(3.1.9'')

where

S is the mechanical system formed by only one material point, the centre of

mass

C , at which we consider concentrated the mass of the whole mechanical system

S. If we write the relation (3.1.9) for the poles O and

′

O , respectively, and subtract

one relation from the other, then we obtain the relation

MO O

′

JJJG

SS ,

(3.1.10)

which may be written in the form

() () ( )

′′

+SSSSSS

(3.1.10')

too, the notations being analogous to the above ones. It is thus put into evidence the

variation of the polar static moment of a mechanical system

S if one passes from a pole

O to another pole

′

O ; projecting on the co-ordinate axes, one obtains corresponding

relations for the planar static moments.

In the case of a plane mechanical system (for which the geometric support

Ω

belongs, e.g., to the plane

0x ), the components of the static moment S

with

respect to a pole in this plane are axial static moments (with respect to the co-ordinate

axes)

OOx

SS xm

αα

Ω

∫

αβ

≠

,1,2αβ

;

(3.1.6'')