Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

(

)

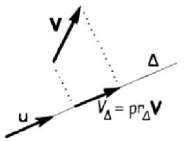
cos , prV

ΔΔ

=⋅= =VVu Vu V

;

(2.1.13)

Figure 2.3. Projection of vector V on the directed axis Δ .

obviously, the projection (which is a scalar) has a sign, as its direction coincides (sign

+) with the direction of

u or not (sign –). One can thus write the scalar product also in

the form

12 1 2 2 1

pr prVV⋅= =

VV V V.

(2.1.12')

We mention following properties:

12 21

⋅

=⋅VV VV (commutativity);

ii)

()

123 1213

⋅

+=⋅+⋅VVV VVVV (distributivity with respect to the addition

of vectors; consequence of the properties expressed by the relations (1.1.7) and

(2.1.13)).

The unit vectors of the co-ordinate axes verify the relations

kjk

δ⋅=ii , ,1,2,3jk

(2.1.14)

where we have introduced Kronecker’s symbol

1for ,

0 for .

⎧

⎪

⎨

≠

⎪

⎩

(2.1.15)

If we express the vectors in the canonical form

Vi,

2kk

Vi,

(2.1.16)

then it follows

12 12

⋅

=VV ,

(2.1.17)

where we took account (2.1.14). In particular, if

(

)

 VV or

()

, π= VV ,

then the vectors are collinear and we may write

12 12

⋅

=±VV

(2.1.18)

as the vectors have or not the same direction; the square of the modulus (1.1.2) of a

vector is given by

Mechanics of the systems of forces

VVV⋅= = =VV V .

(2.1.19)

()

,/2π= VV , then there results

12 12

⋅

==VV ,

(2.1.20)

obtaining thus the necessary and sufficient condition of orthogonality of the vectors

and

V (supposing that

≠

VV 0); obviously, the relation (2.1.20) is verified also if

one of the factors vanishes. It is a case in which one has divisors of zero.

The square of the relation (1.1.4) leads to the modulus of the sum of two vectors in

the form

()

12 12 12

2cos,VVV VV=++ VV .

(2.1.21)

The angle (less than

π ) of two directed axes of vectors

V and

V is given by

()

12 12

cos ,

VV VV

⋅

(2.1.22)

We can write the component of a vector along an axis in the form

⋅Vi, 1, 2, 3j

(2.1.23)

so that the canonical representation (2.1.6) becomes

(

)

=⋅VVii.

(2.1.6'')

As well, the cosines given by (2.1.9) may be expressed by the relations

kj k

′

⋅ii, ,1,2,3jk

;

(2.1.9')

in this case, the scalar products of the relations (2.1.8), (2.1.8') by

′

i and

i , 1, 2, 3l = ,

respectively, lead to the relations

ik jk

αα δ= ,

ki jk

αα δ

, ,1,2,3jk

(2.1.24)

verified by these cosines.

1.2.2 Vector product of two vectors

The vector product (external product, cross product) of the (free, bound or sliding)

vectors

V and

V is a vector

×VVV,

(2.1.25)

MECHANICAL SYSTEMS, CLASSICAL MODELS

the direction of which is normal to the plane formed by the given vectors (supposing

that they are applied at the same point), such that the vectors

V ,

V , V (in this order)

form a positive basis, and the modulus of which is given by

(

)

12 1 2

sin ,VVV

VV ;

(2.1.25')

Figure 2.4. Vector product V of two vectors (a). Vector

′

V of orthogonal projection (b).

hence, the modulus of the vector product is equal to the area of the parallelogram

defined by the two vectors (Fig.2.4,a). Thus, we introduce an oriented plane, which puts

into evidence a positive direction for the angle

(

)

, π

 VV (so that an observer

situated along the vector

V sees the superposition of

V onto

V by a rotation from

right to left, the right-hand rule). The oriented plane element (bounded by a closed

simple curve), corresponding to the previous definition, is called a bivector and is

represented by the vector

V . In contradistinction to the vector associated to an oriented

segment (with the aid of which we have built up the vector space), called also polar

vector, this vector will be called axial vector; the denomination is justified, because it

corresponds to a rotation in the oriented plane, about an axis normal to this plane. We

notice that one cannot sum a vector with a bivector, but one can set up an analogous

algebra of bivectors.

Let

′

V be the orthogonal projection vector of vector

on a plane normal to the

vector

V (Fig.2.4,b); it is easy to see that

12 12

′

×=×VVV VV,

(2.1.26)

because the two vector products lead to axial vectors having the same direction and

modulus. We mention the following properties:

12 21

=− ×VV VV

(anticommutativity);

ii)

()

123 1213

+=×+×VVV VVVV (distributivity with respect to the

addition of vectors; consequence of the property expressed by the relations

(2.1.26)).

If we express the vectors in the canonical form (2.1.16), then there results,

symbolically,

123

1 2 11 12 13

21 22 23

VVV

×=

iii

(2.1.27)

Mechanics of the systems of forces

because

kjkll

×=∈ii i, ,1,2,3jk

(2.1.28)

∈

being Ricci’s permutation symbol

()()

1 for , , 1,2,3 ,

1 for , , 2,1,3 ,

0 for or or ,

jkl

jk kl l j

⎧

⎪

∈=− =

⎨

⎪

⎩

(2.1.29)

where we used the notation (1.1.1). For instance, the component of the vector product

(2.1.25) along the axis

Ox is given by

ljkl k

VVV

∈ ,

(2.1.30)

so that

12 1

kl k l

=∈VV i;

(2.1.30')

this is, in fact, the development of the determinant (2.1.27).

In particular, if

()

,/2π

 VV , then the two vectors are orthogonal and we have

12 12

=VV .

(2.1.31)

()

,0= VV or

()

, π

 VV , then the vectors are collinear and we can write

=VV 0;

(2.1.32)

this relation represents the necessary and sufficient condition of collinearity of the

vectors

and

(supposing that

≠

VV 0

) and is equivalent to a condition of the

form (2.1.4'') (we use the formula (2.1.27)). Obviously, the relation (2.1.32) is verified

also if one of the factors vanishes. It is another case in which one has divisors of zero.

By using the formulae (2.1.12) and (2.1.25'), we deduce Lagrange’s identity

()

12 12 1 2

VV⋅= −×VV V V;

(2.1.33)

from this relation one can obtain also Cauchy’s inequality

()

12 12

VV⋅≤VV .

(2.1.34)

1.2.3 Scalar triple product of three vectors

The scalar triple product (mixed product) of three (free, bound or sliding) vectors

V ,

V and

V is the scalar defined by the right or by the left member of the relation

MECHANICAL SYSTEMS, CLASSICAL MODELS

()

(

)

12 3 1 23

×⋅=⋅×VV V V VV,

(2.1.35)

which is easy verified if one takes into account the expressions (2.1.17) and (2.1.27) of

the scalar and vector products, respectively. The notation of this product in the form

()

[

]

123 12 12

,, det

ij ij

ijk k ijk k

VVVVVVV==∈ =∈VVV ,

(2.1.36)

where we took also (2.1.30') into account, is justified because it is immaterial what

member of the definition relation we use. We have thus obtained the development of a

determinant of third order too. We may also write

[

]

det

mj jm

lmn ijk li nk ijk il kn

VVVVVVV∈∈=∈= , ,, 1,2,3lmn

(2.1.37)

taking into account (2.1.29). Indeed, if two of the indices

,,lmn are equal, for instance

lm= , the product of the quantity

VV , symmetric with respect to the indices i and

j , by Ricci’s symbol

ijk

∈

, skew-symmetric with respect to these indices, vanishes, as

well as

mmn

∈ ; if all the indices ,,lmn are different, for instance

1l =

2m =

3n =

, then we find again (2.1.36). Analogously, we can prove the relation

[]

det

hi ijk lmn hl kn

VVVVδ ∈∈= ,

,1,2,3hi

(2.1.37')

We notice also that the scalar triple product of the vectors

U , V , W may be expressed

in the form

()

ijk k

UVW

∈

UVW

(2.1.38)

The relations (2.1.35), (2.1.36) show that the scalar product of an axial vector by a polar

one has a meaning, because it leads to a scalar; indeed, one can thus introduce the

notion of a mixed product of three polar vectors. We mention the following properties:

()

(

)

(

)

123 4 123 124

,, ,, ,,+= +VVV V VVV VVV (distributivity with respect

to the addition of vectors);

with three vectors

one can form 3! 6

mixed products, which

verify the relations

()

(

)

(

)

123 231 312

,, ,, ,,

=VVV VVV VVV

()

(

)

(

)

213 132 321

,, ,, ,,=− =− =−VVV VVV VVV ,

(2.1.39)

ii)

obtaining thus only two distinct mixed products, which are of opposite sign.

If we denote

=×WVV

, then we may write

()()

(

)

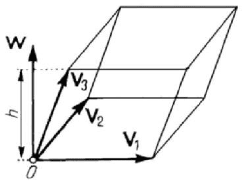
123 1 2 3 3 3

,, cos ,WV Wh=×⋅= =VVV V V V WV ;

(2.1.36')

hence, the scalar triple product represents the volume of the parallelepipedon formed by

the vectors

V ,

V and

V , because W is the area of the parallelogram determined by

Mechanics of the systems of forces

V and

V , while

(

)

cos ,hV= WV is the height of the parallelepipedon (Fig.2.5).

()

,/2π< WV , then the scalar (2.1.36') is positive, while the relation

Figure 2.5. Triple scalar product trihedron.

(

)

123

,, 0VVV ≷

(2.1.40)

represents the condition that the vectors

V ,

V , in the given order, form a positive

(right-handed) or negative (left-handed) basis, respectively. If

(

)

123

,, 0

VVV ,

(2.1.41)

then the corresponding volume vanishes; hence, this is a necessary and sufficient

condition of coplanarity of vectors

V ,

V and

V (supposing that

123

,, ≠VVV 0),

and is equivalent to a condition of the form (2.1.3'''). Obviously, the relation (2.1.41) is

also verified if one of the factors is equal to zero; if two of the vectors

V ,

V are

collinear (in particular, equal), then the mixed product vanishes too (a very important

case in practice).

Starting from the formula (2.1.36) and applying the rule of multiplication of two

determinants, we obtain

()( )

[

]

123 1 2 3

,, , , det

=⋅VVV WWW V W ;

(2.1.42)

in particular, one has

()

[

]

()()

222 2 2

123 123 23 31

, , det 1 cos , cos ,

VVV=⋅= − −

⎡

⎣

VVV V V VV VV

() ()()()

12 23 31 12

cos , 2 cos , cos , cos ,−+

⎤

⎦

VV VV VV VV ,

(2.1.42')

the determinant in the right member being Gramm’s determinant.

Taking into account the geometric signification of the scalar triple product, we may

write

(

)

kl k l

∈=iii;

(2.1.43)

the formulae (2.1.39) show that there are six components, but only two of them are

distinct

MECHANICAL SYSTEMS, CLASSICAL MODELS

kl klj ljk kjl jlk lkj

∈ =∈ =∈ =−∈ =−∈ =−∈

, ,, 1,2,3jkl

(2.1.44)

The permutation symbol is thus skew-symmetric in all pair of indices (hence, it is

totally skew-symmetric).

Two permutation symbols lead to the product

im in

mjn

ijk lmn jl

kl km kn

δδ δ

∈∈ = , ,,,, , 1,2,3ijklmn

(2.1.45)

where we took into account the formulae (2.1.42) and (2.1.14). For

, we obtain

jm im

ijk lmk il jl

δδ

δδ δ δ

δδ

∈∈ = = − , ,,, 1,2,3ijlm

;

(2.1.46)

if we have also

jm= , then it results

ijk ljk il

δ∈∈= , ,1,2,3il

(2.1.46')

and if

il= also holds, then we get

ijk ijk

∈

∈= .

(2.1.46'')

Multiplying the relation (2.1.37) by

lmn

∈

and with the aid of the relation (2.1.46''),

we obtain

[]

det

ijk lmn il kn

VVVV∈∈= .

(2.1.36'')

1.2.4 Vector triple product of three vectors

Let be three (free, bound or sliding) vectors

V ,

V and

V , with which one can

form six distinct vector triple products, equal – in modulus – two by two. Choosing one

of these triple vector products

(

)

123

××VV V V,

(2.1.47)

we note

=×WV V; this is a vector normal to the plane formed by the vectors

and

V . On the other hand, the vector product

×VVW is normal to W ,

belonging to the plane normal to

W , hence contained in the plane formed by

V and

; using the condition of coplanarity of the vectors V ,

and

, we may write

λμ

+VV V

(2.1.48)

Mechanics of the systems of forces

where

λ and μ are – for the moment – indeterminate scalars. This representation of the

vector triple product by means of two polar vectors allows us to affirm that the vector

product of a polar vector by an axial one has a meaning. The relation (2.1.48) holds for

any vectors

V ,

V and

V . We perform a scalar multiplication of both members by

V ; the first member becomes a mixed product with two equal factors, hence vanishing.

We may thus write

()

(

)

12 13

0λμ

⋅

+⋅=VV VV .

Supposing that

0⋅≠VV and

⋅

≠VV , it follows that λ and μ must be of the

form

()

λν=⋅VV,

(

)

μν

−⋅VV,

where

ν is a still undetermined scalar; replacing in (2.1.48) and projecting on the axis

Ox , we can write

(

)

(

)

[

]

13132123

mjjijji

ijk klm l

VVV VVVVVVν∈∈ = − .

If we take into account a formula of the form (2.1.46), then we obtain

1ν =

; thus, the

basic formula of the vector triple product is

()

(

)

(

)

123 132 123

×× =⋅ −⋅VVV VVV VVV.

(2.1.49)

12 13

0⋅=⋅=VV VV , this triple vector product vanishes, but the formula (2.1.49)

still holds; if only one of these scalar products is equal to zero, one obtains also an

identity.

It follows that the vector product is not associative; hence

()

(

)

12 3 1 23

××≠××VV V V VV,

(2.1.50)

in general. But one can verify the relation

()

(

)

(

)

123 231 312

×+××+××=VVV VVV VVV 0.

(2.1.50')

Using the formula (2.1.49), one may easily prove the relations

()()

(

)

(

)

(

)

(

)

1 2 3 4 13 24 14 23

×⋅× =⋅ ⋅−⋅ ⋅V V V V VV VV VV VV,

(2.1.51)

()()

(

)

(

)

1 2 3 4 341 2 234 1

,, ,,

×× = −VV VV VVVV VVVV

()

(

)

412 3 123 4

,, ,,=−VVV V VVV V;

(2.1.51')

the last relation leads to

()()

(

)

(

)

123 23 1 31 2 12 3

,, ,, ,, ,,=++V V V V VV V V VV V V VV V V.

(2.1.52)

MECHANICAL SYSTEMS, CLASSICAL MODELS

In other notations, we may write

()

123

2,,

ijk

kkk

∈

==VVeeee

eee

(2.1.52')

obtaining thus the representation of the vector

V in a positive basis

()

{}

123

, 1, 2, 3, , , 0

k =>eeee; hence, the components of the vector V in this

basis will be

V (in fact, contravariant components, but in what follows we will not use

the notions of covariance and contravariance), corresponding to Cramer’s formulae in

the theory of linear algebraic equations. The representation (2.1.52') constitutes a

generalization of the canonical representation (2.1.6'').

1.2.5 Applications to the study of certain equations

We will consider now two equations, often used in the vector computation. Let thus

be the scalar equation

⋅

=ax ,

(2.1.53)

where

is a given vector, x is a unknown vector, while m is a given scalar. The

solution of the homogeneous equation

⋅

=ax is a vector contained in a plane normal

to the vector

a ; hence, the general solution of this equation is of the form =×xpa,

where

p is an arbitrary vector. Adding a particular solution of the non-homogeneous

equation, we obtain the general solution of the equation (2.1.53) in the form

=×+

xpa .

(2.1.53')

Let be also the vector equation

=ax b, 0

⋅

=ab ,

(2.1.54)

where

and b are given vectors, while x is a unknown vector; we notice that the data

of the problem cannot be arbitrary, because the vectors

a and b must be orthogonal

(otherwise, the vector

b cannot be the vector product of the vectors a and x , and the

equation has not solution). The solution of the homogeneous equation

×=ax 0 is a

vector collinear with the vector

a , hence of the form λ

xa, where λ is an arbitrary

scalar. Introducing a particular solution of the non-homogeneous equation (which is

verified taking into account the canonical formula of the vector triple product and the

condition

0⋅=ab ), one can write the general solution of the equation (2.1.54) in the

form

xa .

(2.1.54')

Mechanics of the systems of forces

2. Systems of forces

A system of forces is a set of forces which can be modelled by bound or sliding

vectors. The fundamental problem is that of replacing a system of forces by another one

of a simpler form, equivalent – from the point of view of its mechanical action – to the

first system; to do this, we use the moment of a force (in general, of a vector) and the

torsor operator. In what follows, let us deal with discrete systems of vectors, very

important in the study of discrete mechanical systems.

2.1 Moments

The notion of moment plays an important rôle in the theory of systems of forces and,

in general, in the theory of systems of vectors. We introduce thus the moments with

respect to a pole or to an axis, for quantities represented by bound vectors, as well as for

quantities represented by sliding vectors; these moments must be considered as being

the result of the application of certain operators on the given vectors. For the sake of

generality, we will obtain these results for arbitrary vectors.

2.1.1 Moment of a vector with respect to a pole

Let be a pole

O and a bound vector V , applied at a point P of position vector r

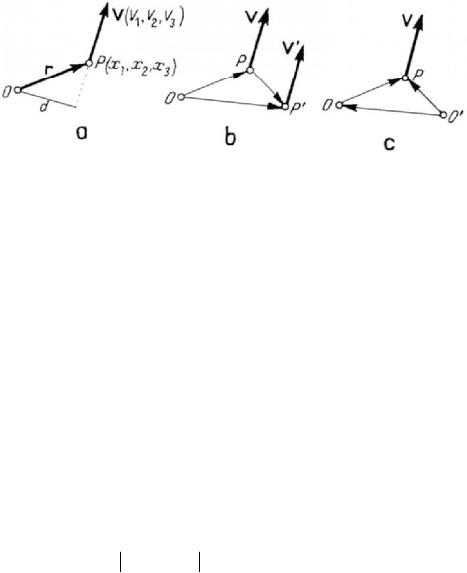
(Fig.2.6,a). The moment of the vector

V with respect to the pole O is, by definition,

the vector product (considered as a bound axial vector applied at

)

Figure 2.6. Moment of a vector with respect to a pole (a). Variation of the point of

application (b) or of the pole (c).

()

OP≡=×=×





MMV VrV;

(2.2.1)

the components of this vector are

Oi ijk k

MxV

∈ , 1, 2, 3i

(2.2.1')

The moment

M vanishes if

V0 (banal case) or if

r0 (the vector is applied at

); as well, it is equal to zero if the vectors V and r are collinear, hence if they have

the same support. We may thus affirm that the moment of a bound vector with respect

to a pole vanishes if and only if the pole is on the vector’s support. If the distance of the

pole

O to the support of the vector V is d (the lever arm of the moment, Fig.2.6,a),

then we can write the modulus of the moment in the form

()

MV .

(2.2.2)