Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

140

conjugate (

1,2

iλαβ=±), then we have i

αγ δ

′

+ , i

αγ δ

′

− ,

1, 2, 3

j =

;

hence,

jj jj jj

αα γγ δδ

′

′′

=+=

, a relation which takes place only if all the terms

vanish. In conclusion, all the roots of the equation (3.1.70) are real; hence, there exist

three principal directions which, in the case of distinct roots, are orthogonal. These

roots represent the eigenvalues of the given matrix, while the vectors along the

corresponding principal directions are the eigenvectors.

If two roots are equal, then the corresponding quadric is of rotation (we have one

principal direction, all the directions contained in the plane normal to this one being

principal directions), while if all the roots are equal, then the quadric is a sphere (all the

directions are principal directions).

The considered quadric is Cauchy’s quadric, corresponding to the symmetric tensor

a .

Because the tensor is a mathematical entity for which the principal directions do not

depend on the system of co-ordinates, it follows that the coefficients

I ,

I are

invariant by a change of co-ordinates. These are the three invariants of the symmetric

tensor

a . An antisymmetric tensor a has only one invariant

222

2233112

aaa=++I ,

(3.1.72)

which corresponds to the modulus of its associate vector. If

′

a is the deviator (of

associate matrix (3.1.60')) of the symmetric tensor, then we get

′

I .

(3.1.73)

Let us suppose that the system of axes

123

Ox x x corresponds to the principal

directions. We may write, e.g.,

1α

0αα

= for

λλ

, and the relation

(3.1.71) leads to

11 1

a λ= ,

12 13

0aa

= for

1, 2, 3

. Hence,

λ ,

1, 2, 3

i =

represent the extreme values of the components

of the principal diagonal,

corresponding to the reduction of the matrix (3.1.58) to a diagonal one and to the

reduction of the quadratic form (3.1.64) to a sum of squares; obviously, we have

1123

λλλ

++I ,

(3.1.74)

2233112

λλ λλ λλ

++I ,

(3.1.74')

3123

λλλ

I .

(3.1.74'')

Using the direction cosines of the axis

Δ with respect to the principal axes, we may

write

222

11 22 3 3

λα λα λα=++.

(3.1.75)

Let be a system of axes

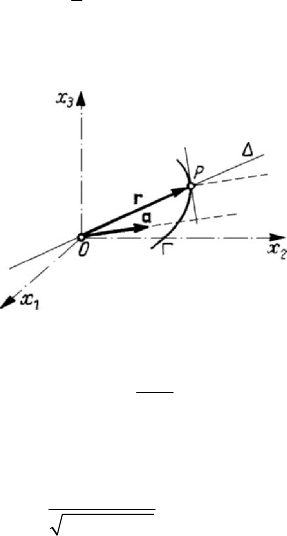
123

Ox x x and a point P of position vector

x=ri on the

axis

Δ (Fig.3.6); it results

Mass geometry. Displacements. Constraints

141

α = , 1, 2, 3i

so that the relation (3.1.66) leads to

Figure 3.6. The

quadric associated to a symmetric tensor of second order.

= .

Let us choose the point

so as to fulfill the condition

sign

ΔΔ

= ;

(3.1.76)

the locus of the point

P , corresponding to all the positions which can be taken by the

axis

Δ , will be just the quadric (3.1.65), obtaining thus a geometric image of the

variation of the component

. The equation of the quadric will be of the form

222

11 22 33

signxxx a

λλλ

′′′

++= ,

(3.1.77)

where the function “sign” has been introduced to get always a real quadric. By

convention, we denote the principal values so as to have

123

λλλ≥≥

. (3.1.78)

0λ > or if

0λ < , then we get an ellipsoid; otherwise, one obtains an one-sheet

or a two-sheet hyperboloid (we notice that both hyperboloids, which are conjugate,

form the considered locus). The relation (3.1.76) shows that the major and the minor

principal axes correspond to

min

and

max

, respectively. If we introduce the vector

a of components

iijj

aaα= ,

1, 2, 3

, then we obtain a direction which coincides

with that of the normal to the surface

constΦ

at the point P (direction parameters

Φ ); hence, the vector

is normal to the plane tangent to the quadric at the point in

which this one is pierced by the axis

Δ (Fig.3.6). We notice that the vector a is along

MECHANICAL SYSTEMS, CLASSICAL MODELS

142

the axis

Δ if the latter one coincides with a principal direction. The equation (3.1.77)

allows us also to express the quadratic form (3.1.64) in the form of a sum of squares.

The three principal directions form a three-orthogonal principal trihedron of

reference

123O . One can prove that the components

a ,

≠

,1,2,3

, get their

extreme values with respect to the trihedron formed by the bisector planes of the

dihedral angles of the principal trihedron, i.e.:

()

λλ±−,

()

λλ±−,

()

λλ±−;

(3.1.79)

the two signs correspond to the two bisectors: the internal and the external one.

Obviously, the greatest value is (

≠

)

()

max

a λλ=−

(3.1.79')

The components

corresponding to the normals to these bisector planes are equal to

()

λλ+

()

λλ+

()

λλ+

(3.1.79'')

respectively.

1.2.4 The moment of inertia tensor

Let be the matrix

11213

21 2 23

31 32 3

xxxxx

xx x xx

xx xx x

III

⎡⎤

−−

⎢⎥

−−

⎢⎥

−−

⎢⎥

⎣⎦

(3.1.80)

formed by means of the axial and the centrifugal moments of inertia. We notice that the

moments of inertia may be expressed in a unitary form, i.e.

(

)

np np np

jnq jp

jk kpq jk kn

Ixxm xxm

ΩΩ

δδ δδ=∈ ∈ = −

∫∫

(

)

lljk k

xx x x m

Ω

δ=−

∫

,1,2,3

(3.1.81)

where

, ,

, ;

Ijk

⎧

⎪

⎨

−

≠

⎪

⎩

(3.1.81')

one puts thus into evidence the moment of inertia tensor

of components

I , which

is a symmetric tensor of second order.

Mass geometry. Displacements. Constraints

143

Let us suppose that through the point

O passes an axis Δ , the direction of which is

given by the unit vector

n of direction cosines

n ,

1, 2, 3

(Fig.3.7). Taking into

account the transformation relations of the components

I by a rotation of the right-

handed orthonormed frame of reference, we get

Figure 3.7. The axial moment of inertia with respect to a given axis.

123

222

123

xxx

jk k

IInnInInIn

==++−

(

)

23 31 12

xx xx xx

Inn Inn Inn

+ ;

(3.1.82)

in a compact form, we may write

()I

⋅In n ,

(3.1.82')

where

In represents a contracted tensor product.

Noting that

(

)

(

)

() ()

jj j j

kk k lljk kk

ruxuxxxxxxuδ××= −⋅ = − = −rur uurr i i,

where

u is a given unit vector, we obtain the remarkable relation

()dm

Ω

×× =

∫

rur Iu

(3.1.83)

Iu being a contracted tensor product too.

Using the results of the previous subsection, we search the directions for which the

axial moments of inertia get their extreme values. These values (the principal moments

of inertia

123

III≥≥) are the roots of the third degree equation in Lagrange’s

multiplier

11 12 13

21 22 23

31 32 33

det

jk jk

III I

II I III

IIII

−

−= − =

⎡⎤

⎣⎦

−

123

0III

−

+−=III,

(3.1.84)

MECHANICAL SYSTEMS, CLASSICAL MODELS

144

corresponding to three directions, orthogonal two by two (the principal directions

1, 2, 3

OOO

), the direction cosines of which are given by the system of homogeneous

equations with non-vanishing solutions

(

)

jk jk k

IInδ−=, 1, 2, 3j

(3.1.85)

to which we associate the supplementary condition

. (3.1.85')

The matrix (3.1.80) is reduced, in this case, to its diagonal form, the corresponding

centrifugal moments of inertia being equal to zero. The coefficients of the equation

(3.1.84) are the invariants of the tensor

I and are given by

1112233123

Oijkljkililil

IIIIIIIIIIδ==∈∈ = ==++ =++I ,

(3.1.86)

()

2223333111122

jm ii jj ij ij

ijk lmk il

II II II I I I I I I=∈∈ = − = + +I

222

23 31 12 2 3 3 1 1 2

III IIIIII−− − = + + ,

(3.1.86')

[]

3 112233 1123 2231

det

jm ij

ijk lmn il kn

II I I I I I I I I I=∈∈ = = − −I

33 12 23 31 12 1 2 3

2II III III−+ = .

(3.1.86'')

123

,,nnn are the direction cosines of the axis Δ with respect to the principal

directions, then we may write

222

11 22 3 3

I InInIn

=++

(3.1.82'')

1.2.5 The two dimensional case

If the support

Ω is contained in the plane

Ox x , then we obtain

0n = and

33 31 32

0III===; the formula (3.1.82) leads to

()

12 12 12

12 12

xx xx xx

IInIn Inn II

=+− = +

()

() ()

12 12

cos 2 , sin 2 ,

xx xx

II xI x+− −nn,

(3.1.87)

where we put into evidence the angle formed by the unit vector

n of the axis Δ with

the co-ordinate axis

Ox ; for an axis Δ

′

normal to the axis Δ , we may write

()()

() ()

12 12 12

cos 2 , sin 2 ,

xx xx xx

III II xI x

′

=+−− +nn.

(3.1.87')

The centrifugal moment of inertia is given by

Mass geometry. Displacements. Constraints

145

()

() ()

12 12

sin 2 , cos 2 ,

xx xx

III xI x

ΔΔ

′

=− +nn;

(3.1.87'')

we notice that we have also

()

III

ΔΔ

′

=−,

(3.1.87''')

where

Δ and

Δ are the two bisectrices of the angle formed by the axes Δ and Δ

′

Equating to zero the derivative of the function

with respect to the argument

(

)

2,xn , we get

()

tan 2 ,

−

n ,

(3.1.88)

obtaining thus the directions for which the axial moment of inertia

attains its

extreme (maximal or minimal) values; in this case, the axial moment of inertia

′

attains its extreme (minimal or maximal) values too. It is easy to verify that for the

angles

(

)

,xn given by (3.1.88) (and only for those angles) the centrifugal moments of

inertia vanish.

The relation (3.1.88) determines two angles

(

)

2,xn , differing by π ; hence, the

searched angles

(

)

,xn differ by /2π . One obtains thus two principal directions,

normal one to the other, denoted by

1O and 2O , to which correspond the principal

moments of inertia

I and

I (

II≥ ), respectively.

To see which of those directions corresponds to the maximal value of

(which

will be denoted by

I ) and which to its minimal value (denoted by

I ), we calculate

the second derivative

()

12 12

2cos2 ,

xx xx

II I

⎡

⎤

=− − +

⎣

⎦

−

(

)

()

12 12

sin 2 ,

xx xx

II I

⎡

⎤

=−+

⎣

⎦

where we took into account also the relation (3.1.88). We suppose that

I ≠ . If

I > and

(

)

min

,/4x π

and

II> or

(

)

min

/4 , /2xππ

and

II< , then the second derivative is positive and we get

min

; otherwise, if

I < and

(

)

min

,/4x π

n and

II> or

(

)

min

/4 , /2xππ

<n and

II< , then the second derivative is negative and we obtain

max

= . The angle

(

)

min

,xn is the smallest positive angle. In conclusion, the principal axis 1O is that

one which makes the smallest angle with the axis

II>

or with the axis

MECHANICAL SYSTEMS, CLASSICAL MODELS

146

Ox if

II> , hence with the axis with respect to which the moment of inertia is the

greatest. If

II= , then we get

(

)

min

,/4x π

n ; in this case

()

4sin2,

= n

and the corresponding direction is

as we have

I >

respectively. If

I =

and

≠

, then we obtain

()

2cos2,

II x

=− − n

and

(

)

min

,0x =n or

(

)

min

,/2x π

n ; if

II> , then

1Ox O≡ and

2Ox O≡ , while if

II> , then

2Ox O

≡

and

1Ox O

≡

. Finally, if

I =

and

II= , then the expression (3.1.88) is indeterminate; any direction passing

through the respective point is a principal direction, while the common magnitude of

the axial moments of inertia is the magnitude of the principal moment of inertia.

We associate thus the diagonal matrix

⎡

⎤

⎢

⎥

⎢

⎥

⎣

⎦

(3.1.89)

to the moment of inertia tensor. The equation (3.1.84) becomes

0II

−

+=II ,

(3.1.90)

with the invariants

112

III II==+ =+I ,

(3.1.90')

12 12

212

xx xx

II I II=−=I

;

(3.1.90'')

the principal moments of inertia are thus given by

()()

12 12 12

1,2

xx xx xx

III III=+±−+.

(3.1.91)

Taking into account the relations (3.1.88) and (3.1.91), the angles made by the

principal directions with the axis

Ox are given also by one of the relations

()

112212

12 2 12 1

tan ,

xxxxxx

xx x xx x

II I II I

IIIIII

−−

====

−−

(3.1.92)

If the relation (3.1.87) is written with respect to the principal axes, then we get

Mass geometry. Displacements. Constraints

147

() ()

()

12 12

cos ,1 sin ,1

II I II

=+=++nn

()

cos 2 ,1

II− n

;

(3.1.93)

the relations (3.1.87') and (3.1.87'') lead to

()()

()

12 12

cos 2 ,1

IIIII

′

=+−− n ,

(3.1.93')

()

sin 2 ,1

III

ΔΔ

′

=− n .

(3.1.93'')

We notice that we have

(

)

()

cos 2 ,1II II

′

−=− n

(3.1.93''')

too.

Figure 3.8. Principal axes of inertia (plane case).

It is easy to see that the centrifugal moment of inertia has an extreme value for the

angles

()

,1 /4π=n and

()

,1 3 /4π

n , hence for the bisectrices of the angles

formed by the principal directions (Fig.3.8). The value of the extreme centrifugal

moments of inertia are given by

()

III

′

=± − ,

(3.1.94)

while the axial moment of inertia corresponding to the bisectrices

and 3O

′

()

III

′

=+.

(3.1.94')

MECHANICAL SYSTEMS, CLASSICAL MODELS

148

Starting from the gyration radii (3.1.30) and (3.1.30'), we may write

(3.1.95)

and

(3.1.95')

respectively, with respect to the principal axes of inertia, obtaining thus the principal

gyration radii; with the aid of (3.1.93), we get

() ()

222 22

cos ,1 sin ,1ii i

+=nn

()()

()

22 22

12 12

cos 2 ,1

ii ii++ − n

(3.1.96)

In the case of a rectangle of sides

a and

we may write

Iab=

()

Iabab=+, ab≥ ,

(3.1.97)

with respect to the two axes of symmetry. For an ellipse of semiaxes

a and

we get

Iab

()

Iabab

=+, ab≥ ,

(3.1.98)

too; if

abR== , we obtain

III R

===

(3.1.98')

for a circle of radius

R . For an annulus of internal and external radii

R and

R ,

respectively, we get

()

III RR

=== −.

(3.1.99)

1.2.6 Three-dimensional geometric representations

Choosing a point

P of co-ordinates

x ,

1, 2, 3i

, on the axis Δ , we introduce a

vector

JJG

, the extremity of which is given by

JJG

, 1, 2, 3i

(3.1.100)

where

0K > is a constant which determines the units; replacing in (3.1.82), we get

Mass geometry. Displacements. Constraints

149

123 23 31 12

222 2

123 23 31 12

222

xxx xx xx xx

Ix Ix Ix I xx I xx I xx K++− − − =;

(3.1.101)

hence, the locus of the point

P is a quadric. If 0I

(the geometric support Ω

belongs to the axis

Δ ), then the quadric is a circular cylinder with the generatrices

parallel to

Δ ; if 0I

≠ , then the quadric has all its points at a finite distance, hence it

is an ellipsoid (Poinsot’s ellipsoid of inertia). Taking into account the relation

(3.1.100), this ellipsoid allows a geometric study of the variation of the moment of

inertia

when the axis Δ rotates about the pole O (determination of the principal

axes, of the principal moments of inertia etc.). If the ellipsoid of inertia is expressed

with respect to the principal axes (the co-ordinates

123

,,xxx are considered to be with

respect to these axes) and if we use the semiaxes

123

,,aaa given by the relations

2222

11 22 33

Ia Ia Ia K===,

(3.1.102)

then we may express this ellipsoid in the form (

123

aaa

≤

≤ )

222

123

222

123

xxx

aaa

;

(3.1.101')

hence, the principal moments of inertia are in inverse proportion to the squares of the

semiaxes of the ellipsoid of inertia. Taking into account the relations (3.1.24) and

(3.1.102), we get the conditions

22222

11111

kl k

aaaaa

−≤≤+

≤

, jklj

≠

≠≠, ,, 1,2,3jkl

(3.1.103)

which must be verified by the semiaxes of the ellipsoid (3.1.101') so as to be an

ellipsoid of inertia; these conditions are superabundant, the inequalities on the right side

being sufficient. To the semi-minor axis of the ellipsoid corresponds the maximal

moment of inertia, while to the semi-major one corresponds the minimal moment of

inertia. If two of the principal moments of inertia are equal (for instance

II= ), then

the ellipsoid of inertia is an ellipsoid of rotation (

); any axis passing through

the pole

O and situated in the plane 12O is a principal axis of inertia. If all the

principal moments of inertia are equal (

123

III

= ), then the ellipsoid of inertia is a

sphere. If the mechanical system admits three three-orthogonal planes of geometric and

mechanical symmetry, then their intersection lines are principal axes of inertia.

Corresponding to the properties mentioned in Subsec. 1.2.4 concerning the centrifugal

moments of inertia, we may state that any axis normal to a plane of geometric and

mechanical symmetry of a mechanical system is a principal axis of inertia for the point

of piercing of the plane by this axis. As well, if a mechanical system has an axis of

geometric and mechanical symmetry, then this one is a principal axis of inertia for all its

points; the corresponding ellipsoid of inertia is an ellipsoid of rotation with respect to

this axis.