Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

170

32 1 5⋅−= degrees of freedom, while for 3n

it has 33 3 6

⋅

−= degrees of

freedom. If we suppose that there are still

6 degrees of freedom for n particles, then

for

1n + particles we have 3( 1) 3( 1) 6nn

−−= degrees of freedom too (we take

into account that the intervention of a supplementary particle introduces only

3 distinct

constraints (Fig.3.23)); we have thus proved, by complete induction, that a non-

deformable discrete mechanical system, without external constraints, has

6 degrees of

freedom for

3n ≥ .

Figure 3.23. Degrees of freedom of a non-deformable discrete mechanical system.

This result holds also in the case of a non-deformable continuous mechanical system,

hence in the case of a rigid solid. It is sufficient to show that the position of a rigid solid

is univocally determined with respect to a fixed frame of reference with the aid of six

independent parameters. Let thus be a fixed frame

123

Ox x x

′

′′′

(having a known position

in space) and a movable frame

123

Ox x x , rigidly connected to the rigid solid

(eventually, the pole

O is taken at the centre of mass of the solid); the pole O is

determined by three parameters (the co-ordinates

000

123

,,xxx of its position vector). To

determine the position of the rigid solid with respect to the fixed frame of reference, it

is sufficient to specify the position of the movable frame with respect to the fixed one

or with respect to a frame

123

Ox x x

with the pole at

and the axes parallel to the

corresponding axes of the fixed frame (Fig.3.24). We denote by

(the line of nodes)

the intersection of the planes

Ox x

′

and

Ox x

. We give a positive rotation of angle

02ψπ≤< to the axis

′

about the axis

so as to coincide with

and a

positive rotation of angle

02ϕπ

≤

to the

-line about the axis

, so as to be

superposed on

; as well, we give a positive rotation of angle

02θπ≤≤

to the

axis

about

so as to coincide with

. The axis

is immediately

obtained, observing that the frame

123

Ox x x

must be a right-handed one. Starting from

the frame

123

Ox x x

, the angles ψ ,

and ϕ , set up in the mentioned order (one

determines firstly the line

, than the axis

and the axis

, and finally the axis

), specify univocally the movable frame, hence they represent three independent

parameters. The angles

ψ ,

and ϕ are called Euler’s angles; the angle ψ is the

precession of the movable frame, the angle

is the nutation of the movable frame,

while the angle

ϕ is the proper rotation of the movable frame, by analogy with the

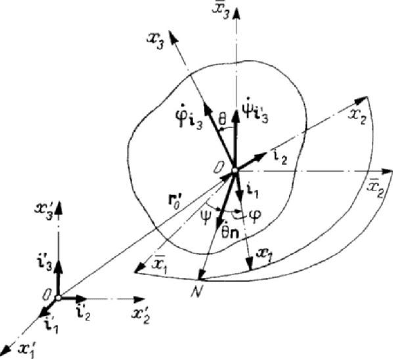
Mass geometry. Displacements. Constraints

171

parameters used in celestial mechanics to determine the position of a planet.

Introducing the column matrices

Figure 3.24. Degrees of freedom of a rigid solid. Euler’s angles ,,ψθϕ.

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

⎡

⎤

′

⎢

⎥

′

⎢

⎥

⎢

⎥

′

⎢

⎥

⎣

⎦

(3.2.11)

of the unit vectors of the co-ordinate axes and the matrices

cos sin 0

sin cos 0

001

ψψ

⎡⎤

⎢⎥

=−

⎢⎥

⎣⎦

10 0

0cos sin

0sincos

θθ

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

−

⎢

⎥

⎣

⎦

cos sin 0

sin cos 0

001

ϕϕ

⎡

⎤

⎢

⎥

=−

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

(3.2.11')

which give the direction cosines of the movable frame axes after a rotation of angle

ψ ,

θ or ϕ , respectively, we may write

′

ΘΨ .

(3.2.11'')

The matrix of the direction cosines of the movable frame axes (

′

⋅ii) will be of

the form

MECHANICAL SYSTEMS, CLASSICAL MODELS

172

cos cos cos sin sin cos sin cos sin cos sin sin

sin cos cos cos sin sin sin cos cos cos sin cos

sin sin sin cos cos

ϕψ θϕψ ϕψ θϕψ θϕ

α ϕψ θϕψ ϕψ θϕψ θϕ

θψ θψ θ

⎡

⎤

−+

⎢

⎥

=− − − +

⎡⎤

⎢

⎥

⎣⎦

⎢

⎥

−

⎢

⎥

⎣

⎦

(3.2.11''')

corresponding to a linear representation of the rotation group

SO(3). Thus, the

position of a rigid solid is univocally determined by six independent parameters (the co-

ordinates

x ,

x and

x of the pole O and Euler’s angles ψ , θ and ϕ ); hence, the

rigid solid has six degrees of freedom.

We can state

Theorem 3.2.1. Any free non-deformable mechanical system (without external

constraints) has six degrees of freedom (excepting the cases of one particle (three

degrees) or of two particles (five degrees)).

2.2.4 Kinematic characterization of constraints

In an inertial frame of reference, the infinitesimal constraints are expressed by

relations between real displacements and the time interval

dt in which these

displacements take place. We may write such a relation in the form

(

)

()

d ;d d , d ,...,d ;d 0

tf t

≡

=rrrr,

(3.2.12)

using real displacements, in the case of a discrete mechanical system

S . Developing

into a power series, we have

... 0

fff=+++=

, (3.2.12')

where

0,1,2,...k =

, are homogeneous polynomials of degree k in

()

x ,

()

x ,

()

x ,

1,2,...,jn

, and dt (the dimensional homogeneity being ensured). If

≠ , then

1,2,...k =

, can be neglected with respect to

, so that we get

≡ ; in this case, the constraint is finite. If

≡

but

≠ , then

2, 3,...k =

, can be neglected with respect to

, and one obtains

. (3.2.12'')

≡ ,

≡ ,…,

−

≡

and 0

≠

, then we may neglect

1, 2,...kj j=+ + , with respect to

, so that the relation (3.2.12') becomes 0

= .

In nature, we do not encounter constraints corresponding to

1j > , so that we will

admit only constraints of the form (3.2.12''). In the case of a discrete mechanical system

S , we express these constraints with the aid of a Pfaff differential form as follows

Mass geometry. Displacements. Constraints

173

dd0

ki k

tα

⋅+ =

∑

rα ,

1,2,...,km

(3.2.13)

assuming that we have

m constraints; by the above reasoning, the coefficients

α and

α cannot depend on the velocities, so that

(

)

;

ki ki

t=ααr ,

(

)

;

tαα= r ,

being functions of class

C . We notice that the relations (3.2.13) can be expressed in

the form

ki k

⋅+ =

∑

vα , 1,2,...,km

(3.2.13')

too, by introducing the real velocities

d/d

vr. We put thus in evidence the

kinematic nature of these constraints; the mechanical system

S cannot have arbitrary

velocities, but only those allowed by the velocity restrictions (3.2.13'). We admit that

the constraints of kinematic nature are distinct, as well as these of geometric nature. In

this case too, we must have

3mn

, so that the motion be possible; the difference

3rnm=−

constitutes the number of kinematic degrees of freedom of the mechanical

system

S . This number vanishes if 3mn

, and the velocities of the n particles may

be determined (eventually, not univocally), by solving a system of

3n equations with

3n unknowns (the components of the velocities of the n particles). If 3mn> , then

the constraints are no more distinct, what was excluded from the very beginning. As in

the case of finite constraints, the constraints considered above are bilateral ones; the

unilateral constraints of a kinematic nature of the mechanical system

S may be

expressed in the form

dd0

ki k

tα

⋅+ ≥

∑

rα , 1,2,...,km

(3.2.14)

or in the form

ki k

⋅+ ≥

∑

vα , 1,2,...,km

(3.2.14')

If the equality cannot take place for one of the constraints, then that one is called a

strict constraint; but the condition

3mn

must still hold.

Passing to the representative space

E , we use the notation (3.2.9), as well as

00kk

bα

()

ki l

α= iα

()

,3( 1)

ki l

bα

−

= ,

1,2,...,in

1, 2, 3l = , 1,2,...,km

(3.2.9')

The representative point

verifies the conditions

dd0

kj k

bX b t

∑

1,2,...,km

(3.2.13'')

MECHANICAL SYSTEMS, CLASSICAL MODELS

174

or the conditions

kj k

bV b

∑

, 1,2,...,km

(3.2.13''')

where

X are the generalized real displacements, while d/d

VXt

are the

components of the velocity of the point

(the generalized velocity) in the

representative space

, in the case of bilateral constraints. The unilateral constraints

(3.2.14), (3.2.14') are expressed in the form

dd0

kj k

bX b t

≥

∑

, 1,2,...,km

(3.2.14'')

or in the form

kj k

bV b

≥

∑

, 1,2,...,km

(3.2.14''')

Let

′

r and

′′

r be two possible displacements which take place in the time

interval

tΔ ; the constraint relations may be written in the form

ki k

tα

′

⋅Δ + =

∑

rα ,

ki k

tα

′′

⋅

Δ+ =

∑

rα , 1,2,...,km

Subtracting and taking into account the relation (3.2.2) which defines the virtual

displacements, we state that the latter ones verify the relations

⋅

δ=

∑

rα

, 1,2,...,km

(3.2.15)

Comparing with relations (3.2.13), we see once more that the virtual displacements

correspond to a certain moment

t and don’t take place in time. Introducing the virtual

velocities (3.2.1'), one may write these conditions also in the form

∗

⋅

∑

vα , 1,2,...,km

(3.2.15')

If we start from possible displacements which satisfy unilateral constraints

ki k

tα

′

⋅Δ + ≥

∑

rα ,

ki k

tα

′′

⋅

Δ+ ≥

∑

rα ,

1,2,...,km

we see that the virtual displacements do not satisfy any constraint relation (by

subtraction, one cannot obtain any conclusion concerning the inequalities), being

Mass geometry. Displacements. Constraints

175

reversible. If in the relations concerning the possible displacements

′′

r there is only

the sign “equal” (the constraints are bilateral), then the virtual displacements which are

obtained verify the relations

⋅

δ≥

∑

rα ,

1,2,...,km

(3.2.16)

corresponding to unilateral constraints; one observes thus that, only in such a case, one

may obtain unilateral constraints for virtual displacements which are irreversible.

Analogously, one can express such constraints also in the form

∗

⋅

≥

∑

vα , 1,2,...,km

(3.2.16')

Xδ are generalized virtual displacements (obtained as differences of generalized

possible displacements

′

Δ and

′

), we may write, for the representative point

in the space

E , the constraint relations in the form (bilateral constraints)

δ=

∑

, 1,2,...,km

(3.2.15'')

or in the form

∗

∑

, 1,2,...,km

(3.2.15''')

where

∗

are generalized virtual velocities (which can be introduced as differences of

generalized possible velocities

′

and

′

); in the case of unilateral constraints

(obtained as we have seen above), we use the relations

δ≥

∑

1,2,...,km

(3.2.16'')

or the relations

∗

≥

∑

, 1,2,...,km

(3.2.16''')

2.2.5 Case of a particle subjected to finite constraints

Let be the case of a single particle

, of position vector r and co-ordinates

123

,,xxx, subjected to finite constraints

()

(

)

123

;,,;0

tfxxxt≡=r , 1, 2k

;

(3.2.17)

MECHANICAL SYSTEMS, CLASSICAL MODELS

176

hence, the particle can be on a surface (we have only

) or on a curve (at the

intersection of two surfaces). A total differentiation with respect to time leads to

conditions imposed to the velocity of the particle, in the form

grad 0

kkkjk

fffvf

=⋅+=+=



v , 1, 2k

;

(3.2.18)

it results

grad

−+



vc, grad

⊥

c ,

1, 2k

(3.2.18')

The component of the velocity along the gradient (along the normal to the

corresponding surface) is given by

grad

=−



, 1, 2k

(3.2.18'')

while its component in a plane normal to the gradient is arbitrary; one obtains thus two

components of the velocity. The total derivative of the relation (3.2.18) with respect to

time leads to conditions imposed to the acceleration of the particle, given by

grad D 0

=⋅+=a , 1, 2k

(3.2.19)

where we have introduced the notation

kkjllkj k

fvv fv f



;

(3.2.19')

we obtain thus the acceleration

grad

−+ac, grad

⊥

c , 1, 2k

(3.2.19'')

Analogously, the component of the acceleration along the gradient is

grad

=− , 1, 2k

(3.2.19''')

while its component in a plane normal to the gradient is arbitrary; we obtain thus two

components of the acceleration.

In the case of a unilateral constraint

(;) 0

t ≥r , 1, 2k

(3.2.20)

Mass geometry. Displacements. Constraints

177

the velocity and the acceleration are not subjected, in general, to any condition. If at a

moment

t the constraint is bilateral ( () 0

), and than it becomes strict

(

()0

tt+Δ > , 0tΔ> ), then we can use a development into a Taylor series

( ) ( ) ) ...

1! d 2!

ft t ft t t

+Δ = + Δ + (Δ +

;

in the frame of this hypothesis, we obtain, for

→ , the conditions d/d 0

t ≥ ,

which may be expressed also in the form

grad 0

⋅

+≥



1, 2k

(3.2.20')

If the constraint is strict, then it acts only on the velocity by which the particle leaves

the surface

= , and not on the velocity by which it reaches the surface (because we

have admitted that

0tΔ> ); the acceleration of the particle remains arbitrary. If we

have

d/d 0

t = at a moment t , then – by an analogous reasoning – we obtain the

constraints

grad D 0

=⋅+≥a

, 1, 2k

(3.2.20'')

2.2.6 Holonomic and non-holonomic constraints

If the Pfaff differential form (3.2.13) is integrable, hence if the first member of the

relation (3.2.13'') is a total differential with respect to the variables

X and t , then the

constraints have been denominated holonomic by Hertz; otherwise, they are called non-

holonomic. We see that the holonomic constraints expressed in the form (3.2.13) are not

infinitesimal, but finite ones, and may be represented in the form (3.2.8); thus, a

holonomic mechanical system is a system with finite constraints or with infinitesimal

integrable constraints (which – in fact – are finite constraints).

The finite holonomic constraints (3.2.8) may be expressed also by means of

infinitesimal displacements in the form (relations of the form (3.2.13)).

dgraddd dd0

ii ii

lllll

ffftfft

= ⋅+=∇⋅+=

∑∑



rr,

(3.2.21)

wherefrom

()

li l

∂

=∇ =

∂

iα , 1,2,...,in

0ll



, 1,2,...,lp

(3.2.21')

The virtual displacements must verify the relations

∇⋅δ=

∑

, 1,2,...,lp

(3.2.21'')

MECHANICAL SYSTEMS, CLASSICAL MODELS

178

Let be two neighbouring, possible, simultaneous (at the moment

t ) positions

r and

+δrr,

1,2,...,in=

, of the same holonomic discrete mechanical system. The

constraint relations are of the form

() 0

r , ()0

δ=rr ,

1,2,...,lp=

Developing into a Taylor series, we may write

()

... 0

jii

∇⋅δ+=

∑

rr;

neglecting the terms of higher order and taking into account the constraint relations, one

obtains the conditions (3.2.21''). One can see once more that

represent the

differential displacements which must be effected by the particles of the mechanical

system to pass from a position to another one, at the same moment

, being thus virtual

displacements, corresponding to the relation of definition (3.2.2).

The relations (3.2.21) lead to the conditions

∇⋅ +=

∑



v ,

1,2,...,lp

(3.2.21''')

which must be verified by the velocities of the particles of the system; obviously, in

these relations only the components of the velocities along the corresponding gradients

of the constraints are involved. For instance, let be the particles

P and

P at an

invariable mutual distance (or two points of a rigid solid); the relation (see Fig.1.18)

()

const

ji ij

r−==rr

(3.2.22)

takes place. Differentiating with respect to time (or applying the formula (3.2.21''')), we

get

ij i ij j

⋅

=⋅rv rv; (3.2.22')

hence, the projections of the velocities of two points of a non-deformable mechanical

system along the straight line defined by them are equal.

In what concerns the conditions imposed to the accelerations, we obtain

=∇⋅+ =

∑

a , 1,2,...,lp

(3.2.23)

where

11 1

nn n

ij i

llijlil

ij i

fvv fv f

== =

=++

∑∑ ∑



, 1,2,...,lp

(3.2.23')

Thus, in the case of the non-deformable two points system considered above, we may

write

Mass geometry. Displacements. Constraints

179

()( )

ij j i j i

⋅−+− =raa vv .

(3.2.23'')

We notice that, in the case of holonomic constraints, the number of degrees of

freedom

s given by the finite displacements is equal to the number of degrees of

freedom

r given by the infinitesimal displacements (sr

The non-holonomic constraints are expressed by relations of the form (3.2.13'),

which represent conditions which must be verified by the real velocities. The total

derivative with respect to time puts into evidence the conditions which are to be

verified by the accelerations of the non-holonomic discrete mechanical system, i.e.,

ki k

⋅+ ⋅+ =

∑∑

, 1,2,...,km

;

(3.2.24)

as in the case of the velocities, only the components of the accelerations along the

parameters

are involved in this case too.

One can make analogous considerations in the representative space

E . Let be

kkj k

bX b tω

∑

, 1,2,...,km

, 3mn

(3.2.25)

a differential form of the first degree, corresponding to the constraint relations

(3.2.13''); these relations lead to a differential equation of the form

ω = . The form

ωω= (for a fixed k ) is (locally) integrable if there exist two functions 0

≠ and g

so that

gω

; the problem is thus reduced to the existence of an integrating factor

for the considered differential equation. One may prove that the functions

and g do

exist (in a sufficiently small neighbourhood) if and only if there exists a form of the

first degree

θ , so that

dωθω=∧, d0ωω

∧

= , (3.2.26)

where we used the external product defined in the App., Subsec. 1.2.1. We introduce

the matrices

⎡⎤

⎢⎥

⎣⎦

Ω ,

11 12 1

21 22 2

ff f

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

⋅

⋅⋅

⎢

⎥

⎢

⎥

⎣

⎦

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

11 12 1

21 22 2

θθ θ

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

⋅

⋅⋅

⎢

⎥

⎢

⎥

⎣

⎦

(3.2.27)