Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

190

indeterminate or impossible); we say that the respective mechanical system (in

particular, the rigid solid) is statically determinate (isostatic). If

6sp

, then the

problem is indeterminate, the mechanical system being statically indeterminate

(hyperstatic, with

6sp+− degrees of statical indeterminacy). The unknowns of the

problem cannot be determined in the case of a rigid solid, because of the limits of the

mathematical model chosen for the solid; if we pass from a rigid to a deformable solid,

closer to the physical reality, completing thus the considered mathematical model, then

there appear supplementary relations which allow the complete solution of the problem.

Finally, if

6sp+<, then the problem is impossible from the point of view of the rest

with respect to a fixed frame of reference (in some particular cases, for special systems

of given forces, the problem could be determinate); in this case, the mechanical system

is a mechanism for which one has

6( )sp

−

+ degrees of freedom. In what follows, we

pass in review some external constraints without friction, which are important in the

case of a rigid solid.

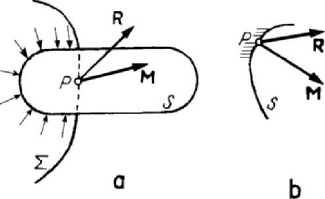
Let

S be a rigid solid, one of the points ()P r of which is constrained to stay on a

perfect smooth fixed surface

Σ (we may suppose that this surface bounds another rigid

solid which – for the sake of simplicity – will be denoted by

Σ too); we say that the

rigid solid has a simple support (movable support) at

P (Fig.3.27,a). To state the

position of the rigid solid, there are necessary only five scalar parameters (e.g., the co-

ordinates

u and v of the point P on the surface Σ and the three Euler’s angles);

hence, a simple support leaves out one degree of freedom of the rigid solid and can be

replaced by a constraint force (a reaction)

N , normal to the surface Σ (as in the case

of a particle constrained to stay on a given surface). If the surface

Σ has at P a

singular point (for instance, an angular point), then the direction of the constraint force

is normal to the surface

S bounding the rigid solid S (Fig.3.27,b); indeed, supposing

that there are two rigid solids

S and Σ , simply leaning one on the other, there arise

two constraint forces

=NN and

−NN, in conformity to the principle of action

and reaction, the force

N being normal to the surface S (hence the force

N too).

Besides the constraints at a contact surface-surface or surface-point considered

above, we mention the constraints at a contact surface-curve, curve-curve, curve-point

or point-point. As well, we can conceive the constraints on a curve in the contact

surface-surface, surface-curve or curve-curve and the constraints on a surface in the

contact surface-surface. One can make analogous considerations in all these cases.

The point of application as well as the support of the constraint force

N are known;

one must determine only its magnitude and its direction (a scalar unknown

N ,

corresponding to a left out degree of liberty; the unknown

N is obtained with the sign

+ or –, as the direction arbitrarily chosen at the beginning is or not the correct one); in

general, the problem is thus determinate. Hence, to fix a rigid solid there are necessary

six simple supports; the six degrees of freedom are thus vanishing and one must

introduce six unknown constraint forces. A simple support may be graphically

represented by a pendulum, indicating the direction in which the possibility of

displacement is suppressed (Fig.3.27,c) or by an idealized support (schematized by a

small cart, Fig.3.27,d), which puts into evidence the directions in which the

displacement is possible. We notice that the directions in which the possibility of

Mass geometry. Displacements. Constraints

191

displacement is suppressed must verify certain conditions so that the rigid solid be

fixed. Indeed, the constraint forces (reactions)

N ,

1,2,...,6j

, will be given by a

linear system of equations of the form

ij j i

aN a

∑

, 1,2,...,6i

;

(3.2.38)

this system has a unique solution if and only if

[

]

det 0

≠

. To fulfill this condition,

it is necessary that: i) the supports of any two reactions do not coincide; ii) the supports

of any three reactions do not be coplanar and concurrent or parallel; iii) the supports of

any four reactions do not be concurrent, parallel or do not belong to the same family of

generatrices of an one-sheet hyperboloid; iv) the supports of any five reactions do not

intersect two straight lines or do not intersect a straight line and be parallel to a plane or

– in general – do not belong to a congruence of the first degree; v) the supports of the

six reactions do not intersect the same straight line or do not be parallel to the same

plane or – in general – do not belong to the same linear complex of the first degree. If

one of these conditions is not fulfilled, then the rigid solid is no more fixed (the system

(3.2.38) is no more compatible). In this case too, the rigid solid may be fixed for certain

systems of forces, but the reactions are no more univocally determined (the rank of the

matrix

[

]

a remains smaller than six). If in a neighbouring position the rank of the

matrix remains smaller than six, then we say that the rigid is not fixed; but if in such a

position the rank is six, then the fixity takes place only for infinitesimal displacements,

not for finite ones (the rigid solid is no more strictly fixed, having to do with critical

constraints).

The simple support may be a bilateral or a unilateral constraint, as the displacement

is hindered or not in both directions of the normal to the surface in contact,

respectively.

Let

S be a rigid solid for which one of the points, ()P r , is a fixed point of the

space (with respect to a fixed frame of reference; eventually, the fixed point may belong

to another rigid solid

Σ ); we say that the rigid solid S has a spherical hinge

(articulation, fixed support) at

P (Fig.3.28,a). To determine the position of the rigid

solid, there are necessary only three scalar parameters (e.g., the three Euler’s angles);

hence, a spherical hinge suppresses three degrees of freedom of the rigid solid and may

be replaced by a reaction

R of unknown direction and magnitude, applied at the point

P (in case of two rigid solids, the reactions

RR,

−RR,

S Σ

+=RR 0,

arise). Hence, the constraint force has three unknown scalars (the components

123

,,RRR of R along three co-ordinate axes). Such a hinge may be obtained by a

sphere of centre

P (the theoretical point of support), with which the rigid solid S

penetrates in a spherical cavity of the rigid solid

Σ ; hence, the possibility of

displacement is suppressed, but the rotation is free (Fig.3.28,b). A spherical hinge is

equivalent, from a mechanical point of view, to three simple supports at the same point,

so that the directions in which the displacement is suppressed do not be coplanar;

hence, a spherical hinge may be represented by three non-coplanar pendulums

MECHANICAL SYSTEMS, CLASSICAL MODELS

192

(Fig.3.28,c) or by an idealized fixed support, denoting the impossibility of displacement

(Fig.3.28,d).

Figure 3.29. Cylindrical hinge (a). Representation by a fixed axis (b). Plane case: two concurrent

pendulums (c) or an idealized fixed support (d).

Let us also consider a rigid solid

for which a straight line passing through a fixed

point

of it (with respect to a fixed frame of reference) represents a fixed axis; in this

case, the rigid solid

has a cylindrical hinge (articulation) at

. Such a hinge may be

obtained by a cylinder passing through the theoretical point of support

, with which

the rigid solid

penetrates in a cylindrical cavity of the rigid solid

; hence, besides

the possibility of displacement, the possibility of rotation about two axes normal to the

fixed axis is hindered too. Remains only the possibility of rotation about the fixed axis;

hence, only a scalar parameter is necessary to determine the position of the rigid solid

(e.g., the rotation angle

, Fig.3.29,a). So that a cylindrical hinge suppresses five

degrees of freedom and can be replaced by a reaction

of unknown direction and

magnitude, applied at

, and by a couple of moment

, applied at

too, and

contained in a plane normal to the fixed axis (the rotation about the fixed axis is not

hindered by not one component of the couple); there are thus introduced five scalar

unknowns (the components

123

,,RRR

of the reaction

and the components

,MM

of the moment, supposing that the fixed axis is parallel to the axis

). A cylindrical

hinge is equivalent, from a mechanical point of view, to a spherical hinge at

(three

non-coplanar pendulums at the same point) and a support at a point

′

of the fixed

axis, formed by two pendulums contained in a plane normal to the axis (Fig.3.29,b); the

reactions at

and P

′

are reduced at

to the torsor

{

}

,RM considered above (with

M normal to the fixed axis).

If the given system of forces is plane, then a spherical hinge contained in this plane

or a cylindrical hinge the axis of which is normal to this plane are replaced by a reaction

R , which has only two components in the plane; in this case, the spherical hinge and

the cylindrical one are equivalent, and we may denote the respective support a plane

hinge (articulation). A plane hinge can be represented by two concurrent pendulums

(Fig.3.29,c) or by an idealized fixed support (Fig.3.29,d).

Taking into account the observations made for the simple supports, we may affirm

that a rigid solid cannot be fixed by means of two spherical hinges (the supports of six

Mass geometry. Displacements. Constraints

193

equivalent pendulums form two stars of concurrent straight lines); as well, the rigid

solid cannot be fixed by a spherical hinge and three simple supports if the supports of

the corresponding pendulums are concurrent or parallel or if they intersect the same

straight line passing through the hinge, or if one of these supports passes through the

hinge. We notice also that, in the case of a given system of forces contained in a plane,

the rigid solid is not fixed by a hinge and a simple support if the support of the latter

pendulum passes through the hinge (obviously plane).

Figure 3.30. Built-in support (a). Graphical representation (b).

A support which suppresses all six degrees of freedom of a rigid solid

S is called a

built-in (embedded) support (a rigid fixing). A built –in mounting may be obtained by

an extremity of a rigid solid

S which penetrates in a rigid solid Σ , the latter one

ensuring its fixity (Fig.3.30,a). On the whole surface of contact between the rigid solids

S and Σ there appear constraint forces which cannot be determined in the frame of

the rigid model considered; but the effect of this support may be replaced by the torsor

of these forces at the theoretical point

P (in fact, an arbitrary point): a reaction R and

a couple of moment

M (six unknown scalars ,

RM, 1, 2, 3i

, corresponding to the

three axes of co-ordinates). A built-in support is equivalent, from a mechanical point of

view, to six simple supports on the contact surface, which verify the necessary

conditions mentioned in this case to obtain the fixity of the rigid solid, hence it can be

represented by six pendulums which satisfy these conditions. Graphically, one can

represent a built-in support (Fig.3.30,b). In the case of a given system of forces

contained in a plane

constx = , by suppressing the six degrees of freedom which

remain one must introduce only three scalar unknowns (

R ,

R and

MM= ).

Besides the basic supports of the rigid solid, considered above, one may conceive

also other ones, which are obtained – in general – starting from those previously

considered. All the supports represent ideal external constraints of the rigid solid, which

verify the relation (3.2.36).

But the rigid solid is a holonomic and scleronomic mechanical system, the external

constraints being scleronomic too; in this case, the real elementary work of the

constraint forces will vanish as well. We may write

(

)

dd d d

jj j j

RPP P

jj j

WtPPt=⋅=⋅=⋅+×

∑∑ ∑

JJJG

Rr Rv Rvω

()

jjj

PPP

PP t t

⎛⎞

=⋅ +⋅ × =⋅+⋅

⎜⎟

⎝⎠

∑∑

JJJG

vR R RvMωω,

MECHANICAL SYSTEMS, CLASSICAL MODELS

194

where we took into account the formula (5.2.3') (see Chap. 5, Subsec. 2.1.1), which

links the velocities of two points

P and

P of the rigid solid, the sums (eventually,

integrals) corresponding to all the points of the solid upon which act constraint forces;

we put thus into evidence the resultant of the constraint forces, as well as their moment

with respect to the theoretical point

P of support (the torsor of these forces at P ).

Hence, the condition of ideal external constraints at the point

P is of the form

(

=vv,

=MM)

ii i i

Rv M ω⋅+ ⋅ = + =Rv M

(3.2.39)

and may be verified in the considered particular cases. For example, in the case of a

support on the plane

constx

we have

and

12 1

RRM

0M==; hence, the condition (3.2.39) holds and the constraint force

0R ≠ is put

in evidence. In the case of the coupling screw-nut, the advance being along the axis

Ox , we have

0ωω==,

0vv

= and

(/2)vpπω

, where p is the screw

pitch, while

0ωω=≠ is the angular velocity (as one can see in Chap. 5, Subsec.

1.3.3); we get thus

(/2)Rp Mπω ω

[

]

(/2) 0pRMπω

+=, and the

constraint forces

123 1 2

,,, ,RRRM M and

(/2)MpRπ

− are put into evidence.

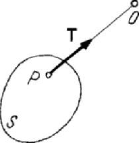
Figure 3.31. A thread acted upon by a tension T .

All the constraints considered above are holonomic ones, of geometric nature, and

the results obtained are useful in the static as well as in the dynamic case; various

examples of non-holonomic constraints, of kinematic nature, have been presented in

Subsec. 2.2.6. All these constraints have been bilateral ones; but we can imagine

unilateral constraints too, obtained with the aid of threads. A thread is considered to be

perfectly flexible and inextensible; hence, the distance between the ends of a thread

may diminish, but cannot grow. If a rigid solid is linked to a fixed point by a thread

perfectly stretched (threads passing over pulleys, rigid solids oscillating at the end of a

thread etc.), then a constraint force

T (always of traction, it draws the rigid solid),

arises along the latter one (Fig.3.31); this force is called tension, while

−T stretches

the thread. The corresponding constraint suppresses one degree of freedom of the rigid

solid and introduces only one scalar unknown (the tension of modulus

T ), if the

direction of the thread is fixed.

2.2.11 Constraints with friction

As we have seen in the case of a particle

P constrained to stay on a fixed smooth

surface

S of equation

(

)

123

,, 0

xxx

, a normal constraint force grad

λ=N ,

Mass geometry. Displacements. Constraints

195

where

λ is a scalar to be determined, arises. If the surface is rough, then the constraint

is no more ideal, while the constraint force

R is no more normal to the surface; there

appears a component

T of this force, contained in the plane tangent at P to the surface

and which has an opposite direction with respect to the component in this plane of the

resultant of the given forces to which is subjected the particle

P . To can determine the

force of sliding friction (it hinders the sliding of the particle

P on the surface, hence

the displacement of the particle in the frame of this constraint) one must make

supplementary hypotheses. The most usual model which corresponds in many cases to

the physical reality is that due to Coulomb; in this case, the modulus of the friction

component is given by (experimentally established for the first time by Amonton in

1699)

TfN

≤

, (3.2.40)

the equality taking place in the limit case of rest (if the inequality takes place, then the

particle

P is at rest on the surface). The numerical coefficient

, which depends only

on the nature and the state (dry or wet) of the rough surface, and does not depend on the

velocity

v of the particle if it begins to move, is called coefficient of friction

(coefficient of static friction, unlike a dynamic one, which is of the form

()

fv= ).

We introduce also the angle of friction

ϕ , defined by the relation

tan

. (3.2.41)

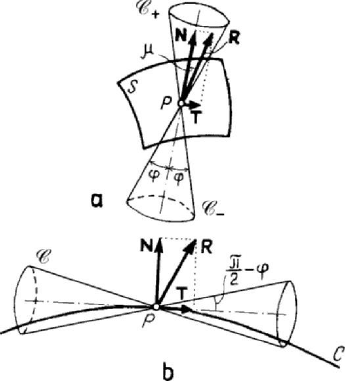
Figure 3.32. Particle P on a surface S (a) or on a curve C (b) with friction.

The relation

/tantanTN μϕ=≤ leads to μϕ

≤

, in this case (Fig.3.32,a); hence,

for rest, the angle

μ between the constraint force R and its normal component N

must be smaller or at the most equal to the angle of friction

ϕ . We are thus led to

MECHANICAL SYSTEMS, CLASSICAL MODELS

196

construct a circular cone

C with the vertex at P and the axis normal to the surface S ,

the vertex angle being

2ϕ (the cone of friction). For rest, in the case of a bilateral

constraint, the support of the constraint force

R must be contained in the interior of the

zone

C or of the zone

−

C of the cone C, or on the cone itself; if the constraint is

unilateral, then we take into consideration only the zone

C (or

−

C ) of the cone of

friction, situated in the part of the surface

in which the particle

may be.

In the case of a particle

constraint to stay on a smooth curve

, of equations

(

)

123

,, 0

xxx = , 1, 2i = , arises a constraint force

1122

grad grad

fλλ

contained in the plane normal to the curve at

, where

,λλ

are scalars which must

be determined. As in the previous case, if the curve is rough, then we introduce a force

of sliding friction

of the form (3.2.40), along the tangent to the curve at

. For

equilibrium, it is necessary and sufficient that the angle between the support of the

constraint force

and the tangent to the curve be greater or at least equal to /2πϕ−

(Fig.3.32,b). We are thus led to consider a circular cone of friction

C, the axis of which

is tangent to the curve

C at

, the vertex angle being

2πϕ

−

. For rest, it is necessary

and sufficient that the support of the reaction

be situated in the exterior of the cone

C or on it.

In both cases considered above, the problem of the position of rest is indeterminate;

in fact, we specify only the corresponding limit positions. In the case of a discrete

mechanical system

S of particles, subjected to constraints with friction, the degree of

indetermination is greater, because neither the directions of the forces of friction are not

known. To solve the problem, we must know the motion by which the system

reached the position of rest, to can determine the forces of friction sufficient to maintain

it in this position, or we must search the forces of friction by which the system

S can

pass once more from the state of rest in a state of motion.

If the friction does not take place between a particle and a rigid surface (or curve),

but between a particle and a fluid (liquid or gas), then we have to do with a viscous

friction, and a coefficient of viscosity appears too. The constraint force is – in this case –

a force of resistance.

2.2.12 Constraints with friction of a rigid solid

Let be the rigid solids

S and Σ simply supported at P , considered at Subsec.

2.2.10 (Fig.3.27,a). In reality, the solids are deformed in the neighbourhood of the point

P , so that the contact is obtained on a small surface on which appear constraint forces

(Fig.3.33,a); by reducing this system of forces at the point

P , we obtain the

corresponding torsor (the constraint force

R and the constraint couple of moment M ),

which replaces the action of the solid

Σ upon the solid S (Fig.3.33,b). The normal

constraint force

N (ideal constraint), the constraint force T , contained in the tangent

plane (corresponding to the sliding friction), the couple of moment

M , normal to the

tangent plane (corresponding to the pivoting friction, which is opposed to the rotation

about this normal), and the couple of moment

M , contained in the tangent plane

(corresponding to the rolling friction, which is opposed to the rotation about an axis in

Mass geometry. Displacements. Constraints

197

the tangent plane, passing through

P ) (Fig.3.33,c) are thus put into evidence. Hence, in

the case of the rigid solid, the friction phenomenon has a more complex aspect.

Figure 3.33. Zone of contact between the rigid solids

and

(a). The constraint force

and

the constraint couple of moment

M (b) and their components (c).

Let us consider the rigid solids S and Σ in contact; as well, let Q be the

component of the given forces along the normal to the common tangent plane and

=−NQ the corresponding ideal constraint force (Fig.3.34,a); besides the component

N of the constraint force R , arises a tangential component too, which is opposing to

the tendency of sliding of the solid

S with respect to the solid Σ . This component

appears even if one of the solids does not slide with respect to the other one (because of

the roughness of the surfaces in contact), having the tendency to equate to zero an

Figure 3.34. Two rigid solids S

′

and Σ in sliding friction contact: the case of friction (a); the

angle of friction (b); the quadrangle of friction (c).

eventual given tangential force which could produce such a sliding; in this case, we

have to do with a friction of adherence (of adhesion), which is opposed to the tangential

component of the given forces. In the limit case in which the solid

S begins to slide on

the solid

Σ , one obtains the force of sliding friction T (the friction of motion); we

suppose that this force is of Coulombian nature and is given by a formula of the form

(3.2.40), where the coefficient

of sliding friction (3.2.41) does not depend – in

general – on the relative velocity of sliding of the two solids or on the magnitude of the

surfaces in contact, but only on their nature (roughness). Numerical values of the

MECHANICAL SYSTEMS, CLASSICAL MODELS

198

coefficient

are given in Table 3.1. An example of dependence of the velocity (for

greater values) is given in Table 3.2 for metal on metal. Also in this case, a cone of

friction of vertex angle

2ϕ is introduced, and the resultant of the constraint forces must

be in its interior or on it. If the given forces are contained in a plane passing through the

point of contact

P , then the problem has a plane character, the cone of friction being

reduced to an angle of friction (the trace of the cone of friction on the considered plane)

(Fig.3.34,b). Let us consider a rigid solid acted upon by coplanar forces and leaning

with friction at the points

P and

P on the surfaces

Σ and

Σ , respectively; the

conditions

111

TfN≤ ,

222

TfN

≤

are put. The angles of friction constructed at these

points determine a quadrangle called the quadrangle of friction (Fig.3.34,c); the state of

rest is possible if the point of piercing

I of the supports of the constraint forces

R and

R is in the interior of the quadrangle or on it. If the system of given forces is not

plane, then one can take into consideration the three-dimensional domain obtained by

the intersection of the two cones of friction.

Table 3.1

wood on wood, dry …………. 0.25-0.50 leather on metals, dry ……….. 0.56

wood on wood, soapy ………. 0.20 leather on metals, wet ……….. 0.36

metals on oak, dry ………….. 0.50-0.60 leather on metals, greasy ……. 0.23

metals on oak, wet ………….. 0.24-0.26 leather on metals, oily ………. 0.15

metals on oak, soapy ……….. 0.20 steel on agate, dry …………… 0.20

metals on elm, dry ………….. 0.20-0.25 steel on agate, oily …………... 0.107

hemp on oak, dry …………… 0.53 iron on stone ………………… 0.30-0.70

hemp on oak, wet …………… 0.33 wood on stone ………………. 0.40

leather on oak ……………….. 0.27-0.38 earth on earth ……………….. 0.25-1.00

metals on metals, dry ……….. 0.30 earth on earth, wet clay ……... 0.31

metals on metals, wet ……….. 0.15-0.20 metals on ice ………………… 0.01-0.03

smooth surfaces, best results ... 0.03-0.036 smooth surfaces, occasionally

greased ………………………

0.07-0.08

Table 3.2

v (km/h)

0 10.93 21.08 43.5 65.8 87.6 96.48

0.242 0.088 0.072 0.07 0.057 0.038 0.027

To put into evidence the rolling friction we will consider the contact between a

circular wheel of radius

R and a horizontal plane. The wheel can be acted upon by the

afferent vertical given force

Q , by a horizontal given force F and by a turning

moment

M . If the local deformation is not taken into consideration, then there appears

only the normal constraint force

−NQ

(Fig.3.35,a). In reality, in the neighbourhood

of the point

P arise local deformations, hence constraint forces on a relatively small

but finite surface (Fig.3.35,b); besides the normal constraint force, one can thus put into

evidence the tangential constraint force

−TF and the moment of rolling friction

M of modulus

MFrNe== (in the absence of the turning moment) (Fig.3.35,c,d).

This is the case of the drawn wheel. Because the position of rest can take place only for

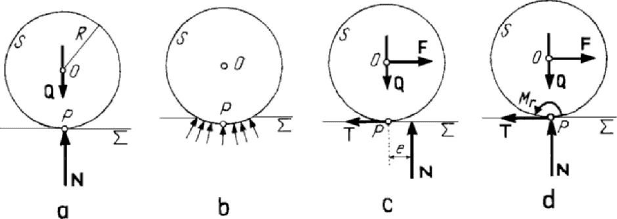
Mass geometry. Displacements. Constraints

199

limited values of the modulus of the force

F , it follows that – in fact –

M and e take

limit values; if

max

es=

, then – with necessity – arises the condition

Figure 3.35. The case of rolling friction: without (a) and with (b) local deformations; the

moment of rolling friction (c,d).

MsN

≤

, (3.2.42)

where

s is a coefficient of rolling friction and has the dimension of a length (the

maximal parallel displacement of the support of the reaction

N with respect to the

point of contact

, so as to oppose to the motion of rolling; it depends only on the

nature of the solids in contact). But besides the friction of rolling arises a friction of

sliding too, so that: if

TfN

≤

MsN

≤

(hence if /

MN fRs≤≤ or if

MNs fR≤≤ ), then the solid is in rest, if TfN

≤

MsN> (hence if

sMN fR<≤), then the solid is rolling without sliding, if TfN> ,

MsN≤

(hence if

RMNs<≤), then the solid is sliding without rolling, while if

TfN> ,

MsN> (hence if /

RsMN

< or if /

sfRMN

< ), then the

solid is sliding and rolling at the same time. In the case of a motive wheel intervenes a

turning moment

too; one can prove that, if the horizontal plane is too smooth (the

coefficient

is too small), then the wheel does not move, neither for a very great

turning moment

M . The problem of the contact of a circular wheel with an inclined

plane may be studied analogously.

Let us consider two solids

S and Σ in contact; because of their local deformation,

the contact takes place on a surface

σ (Fig.3.36,a). We suppose that the solid S is

acted upon by a vertical force

Q and by a couple of moment M along the common

normal; this solid has the tendency to rotate about this normal, maintaining unchanged

the surface of contact, hence the tendency of pivoting if

M is greater than a minimal

value. In fact the pivoting is a sliding on the surface of contact

σ ; on an element of area

dσ arises a force of sliding friction of magnitude ddTfnσ

( dσn is the reaction

normal to the element of area

dσ , while

is the coefficient of sliding friction), at a

distance

r from P , in a direction normal to the vector radius (Fig.3.36,b); the moment

of pivoting friction

M , of modulus

M , must verify the condition

Mfnr

σ≤

∫

;

(3.2.43)