Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

200

if the force

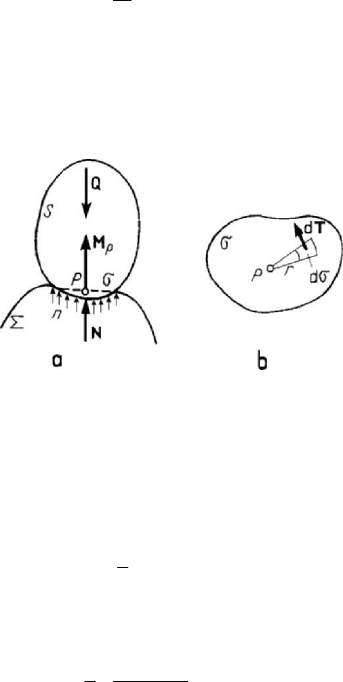
is uniformly distributed on the surface of contact, then we have

//nQ Nσσ==, so that

Mf r

≤

∫

(3.2.43')

where the integral is of the nature of a scalar geometric static moment. This condition is

of the form

MaN

≤

, (3.2.43'')

Figure 3.36. The case of pivoting friction: zone of contact (a); the local constraint (b).

where

a is a coefficient of pivoting friction, having the dimension of a length (it

depends only on the geometry and the nature of the surface of contact and not on the

magnitude of this surface or on the velocity of the motion of pivoting). If the surface of

contact is circular, of radius

R , then one obtains

afR= ;

(3.2.44)

as well,

−

(3.2.44')

in the case of an annular surface of contact of external radius

R and internal radius

R .

Other cases of supporting with friction (e.g., friction in articulations, eye joints,

bearings etc.) may be studied in an analogous manner, using the basic results

considered above.

Chapter 4

STATICS

As we have seen, statics deals with the equivalence of the systems of forces (in

particular, the equivalence to zero) which act upon a mechanical system; it is thus

studied a particular case of motion, that is the case in which a mechanical system,

subjected to the action of a system of forces, remains at rest with respect to a given

(inertial) frame of reference. We will thus consider the statics of discrete or continuous

mechanical systems, especially the problems which arise in the statics of rigid solids.

1. Statics of discrete mechanical systems

In the study of the problems of discrete mechanical systems, we start from the case

of a single particle; the results thus obtained may be extended to the case of other

mechanical systems.

1.1 Statics of the particle

We deal successively with the case of a free particle and with the case of a particle

subjected to constraints; as well, we make some considerations concerning the stability

of the equilibrium of a particle.

1.1.1 The free particle

By free particle (material point) we understand that one which may take any position

in the space; this position depends only on the forces acting upon the particle and is

independent of any geometric or kinematic restriction. A free particle (in

E ) has three

degrees of freedom, its position being specified by three independent parameters (e.g.,

the co-ordinates

x ,

1, 2, 3j =

, the components of the position vector r of the

corresponding geometric point).

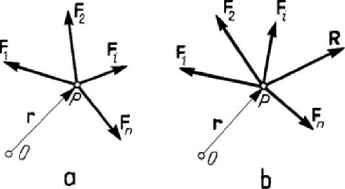
We consider a body which may be modelled as a particle. The forces

F ,

1,2,...,in= , which act upon this body are – in this case – concurrent forces, and can

be modelled as bound vectors (Fig.4.1,a). Applying to this system elementary

operations of equivalence, we obtain the resultant

i =

∑

(4.1.1)

201

MECHANICAL SYSTEMS, CLASSICAL MODELS

202

which is an invariant of the respective system; hence, two systems of forces, which are

acting upon the same particle, are equivalent if they have the same resultant

F .

Figure 4.1. Statics of a free (a) or constraint (b) particle.

Let be a free particle

P which is not acted upon by any force, at rest with respect to

an inertial frame of reference. Let us suppose that this particle is then subjected to the

action of a system of concurrent forces. The principle of the parallelogram of forces

allows us to replace the given system of forces by its resultant, while the principles of

inertia and of initial conditions allow us to affirm that the state of rest is maintained if to

the particle is no more applied any force (or is applied a force equal to zero). If the

system of concurrent forces has a zero resultant (it is equivalent to zero), then we say

that this system of forces is in static equilibrium (if no confusion may occur, then it is

sufficient to say that the system of forces is in equilibrium); in this case, the particle

remains at rest with respect to the considered inertial frame of reference (sometimes we

say that the particle is in equilibrium). In conclusion, the necessary and sufficient

condition of equilibrium (of rest; here and in what follows we exclude the possibility of

a rectilinear and uniform motion, foreseen by the principle of inertia) of a particle

P ,

with respect to a given frame of reference, is written in the form

(4.1.2)

or, in components, in the form

, 1, 2, 3j

. (4.1.2')

In the case of a system of forces which have the same support remains only one scalar

condition, while in the case of a coplanar system of forces, two scalar conditions must

be fulfilled.

The first basic problem is that in which there are given the forces which act upon the

particle, and one must search the position of equilibrium; the unknowns are – in this

case – the parameters specifying the position of the particle (one, two or three

parameters, as we are in a particular case – in

or in

– in what concerns the

system of forces or, in the general case, in

). If the system of equations of

equilibrium is indeterminate, then there exists an infinity of possible positions of

equilibrium, while if this system is impossible there is not one position of equilibrium.

In the second basic problem, the position of equilibrium of the particle is given,

while the forces which act upon the latter one to maintain this position must be

Statics

203

obtained. In this case, the unknowns are the magnitudes and the directions of the forces,

the corresponding solution being – in general – indeterminate. If certain conditions are

imposed to those forces in what concerns their number, directions or magnitudes, then it

is possible that the solutions be determinate; it is necessary that the number of the scalar

unknowns thus introduced be at the most equal to three (or to two in the case of

coplanar forces).

We notice also the case of the basic mixed problem, in which a part of the three

unknowns are elements specifying the system of forces, the other unknowns being

parameters which determine the position of equilibrium.

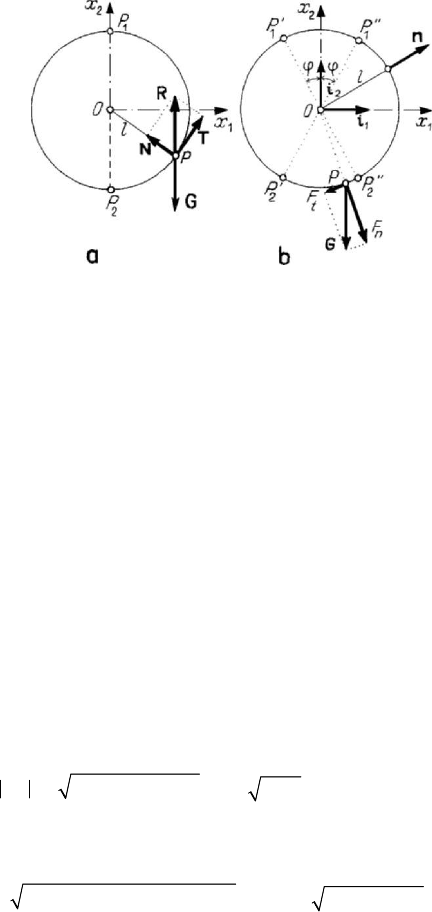
Figure 4.2. Heavy particle in equilibrium: free (a) or constraint (b) particle.

To illustrate the considerations made above, let be, in a vertical plane, a particle

(materialized by a small annulus) of weight

G , linked by two inextensible threads

which pass over two small pulleys

S and

S and are tensioned by the weights

Q and

Q , respectively (Fig.4.2,a). Because the particle is free and subjected to a system of

coplanar forces, we may choose as unknown parameters (we are in the case of the first

basic problem) the angles

α and

α made by the two threads with the horizontal line,

respectively. The threads are extended by the tensions

T and

T , respectively, for

which we have

111

Q==TQ and

222

=TQ , respectively, so that the

particle is acted upon by the forces

G ,

T and

T , which must be in equilibrium.

Projecting on the horizontal and the vertical, we get

1122

cos cos 0QQαα−=,

1122

sin sin 0QQGαα

−=,

wherefrom

222

sin

GQQ

+−

= ,

222

sin

GQQ

+−

= .

(4.1.3)

We notice that the conditions

222

12 1

2GQQ GQ+− < ,

222

21 2

2GQQ GQ+− <

must hold; the equalities never take place, because the pulleys

S and

S cannot be on

the same vertical. These conditions may be written in the form

12 1

GQ Q GQ−<<+,

21 2

GQ Q GQ

−

<<+

(4.1.3')

MECHANICAL SYSTEMS, CLASSICAL MODELS

204

too, corresponding to the conditions verified by the sides of a triangle (the polygon of

the forces

G ,

T and

T ); otherwise, the equilibrium is impossible, and the particle

cannot remain at rest. The position of equilibrium depends, obviously, on the position

of the pulleys

S and

S ; for instance, if the pulleys

S and

S are on the same

horizontal, then the conditions which must take place become

222

0 GQQ<+−

2GQ<

222

21 2

02GQQ GQ<+−< .

The intervening threads do not introduce any restriction of geometric nature so that

the above considered problem is that of a free particle. If the particle would be linked

by one of the threads (considered inextensible) to a fixed point (a ring), then it should

be on a circle, the centre of which is at this fixed point (Fig.4.2,b).

1.1.2 The constraint particle

If a particle P is subjected to constraints, which will be considered scleronomic,

then the latter ones have an influence on the conditions of equilibrium, hence on the

position of rest, diminishing the number of degrees of freedom of the particle. As it was

shown in Chap. 3, Subsec. 2.2.1, the axiom of liberation from constraints (the axiom of

liberation, the axiom of constraints, the axiom of constraint forces) allows us to replace

these constraints by constraint forces (reactions); in this case, the particle

P may be

considered to be a free particle, subjected to the action of the given as well as of the

constraint forces, so that one can use the considerations of the previous subsection. If

R is the constraint force applied to the particle P (in fact, the resultant of all

constraint forces acting upon this particle), which is subjected also to the action of the

system of given forces

F , 1,2,...,in

, then the necessary and sufficient condition of

equilibrium (of rest with respect to a given frame of reference) is of the form (Fig.4.1,b)

=FR 0

(4.1.4)

or, in components, of the form

= , 1, 2, 3j

. (4.1.4')

In the case in which the given and the constraint forces are coplanar, only two scalar

conditions must be fulfilled, while if these forces have the same support, then only one

scalar condition remains.

The unknowns of the problem are of two kinds: unknowns corresponding to the

parameters which specify the position of equilibrium and unknowns which

determine the constraint force (the basic problem is thus a mixed one); some

conditions which must be verified by the given forces so as the particle be at rest

with respect to a given frame of reference there arise. If no condition is imposed to

the constraint force, then the problem is indeterminate (the number of the

components of the constraint force is equal to the number of the equations of

equilibrium, but there intervene also the parameters specifying the position of

equilibrium), excepting the case in which the particle is constrained to be at a

certain fixed position in the space; in the latter case, we have

Statics

205

=−RF,

− ,

1, 2, 3j

. (4.1.5)

To point out the restrictions which may be imposed to the constraint force

R , we

will effect the decomposition

+RNT, (4.1.6)

Figure 4.3. Heavy particle constraint to stay on a circle in a vertical

plane: without friction (a), with friction (b).

where the components

N and T do not allow the particle to leave the constraint or to

move in the frame of it, respectively. Let us consider, for instance, a particle

P of

weight

G , which may remain in equilibrium on a fixed circle, in a vertical plane

(Fig.4.3,a); the component

N of the constraint force is in the direction of the normal to

the circle, being the normal reaction, while the component

T is tangent to the circle,

representing a constraint force with friction (the force of friction). The problem will be

studied in Subsecs. 1.1.5 and 1.1.8.

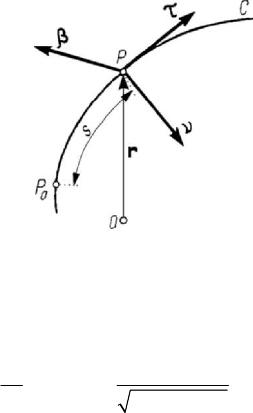
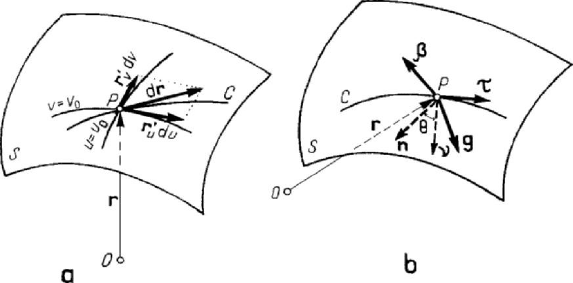
1.1.3 Geometry of a curve. Frenet’s trihedron

Let be a curve C defined by the parametric equations

()

xxq= ,

[

]

,qQ qq

∈

≡ , 1, 2, 3j

(4.1.7)

where

()

xCQ∈ ; a point P is specified by the position vector () ()

qxq=ri

(Fig.4.4). Introducing the derivative

()q

′

r and the differential dr , and taking into

account the metrics of the space

E , we may write

222

123

dddd

xxxqxxqs

′′′ ′′

=++ = =r ,

(4.1.8)

where the curvilinear abscissa represents the length of the arc of curve

PP, given by

222

123

() () () ()d () ()d

sq xu xu xuu xuxuu

′′′ ′′

=++=

∫∫

(4.1.8')

MECHANICAL SYSTEMS, CLASSICAL MODELS

206

A point of the curve

C for which the derivative of the position vector is non-zero is

called an ordinary point; a non-ordinary point is called singular. In what follows we

consider only ordinary points. An osculating circle at an ordinary point

P on the curve

C is the limit to which tends a circle defined by the point P and two other

neighbouring points if the latter ones tend to the point

P ; the osculating circle is

tangent to the curve at this very point and is an approach of the curve in the

neighbourhood of the respective point. The plane normal to the tangent at this point is

called normal plane; the straight lines which pass through the point

P and belong to

this plane are normals to the curve

C . The plane in which lays the osculating circle is

called the osculating plane; this plane contains the tangent to the curve too. The centre

of the osculating circle (called also the circle of curvature) lies on the normal to the

curve at the point

P , contained in the osculating plane; this normal is called the

principal normal. The plane normal to the principal normal (which contains also the

tangent to the curve) is called the rectifying plane; the normal contained in this plane is

called binormal. Hence, the osculating plane is formed by the tangent and the principal

normal, the normal plane is formed by the principal normal and the binormal, while the

rectifying plane is defined by the binormal and the tangent. In the case of a plane curve,

the osculating plane coincides with the plane of the curve. At the point

P , we introduce

a local frame of reference (a movable frame), that is the intrinsic Frenet’s trihedron

(sometimes denoted as the Serret-Frenet trihedron); this one is a three-orthogonal

trihedron, the unit vectors of the corresponding co-ordinate axes being defined as

follows: the unit vector τ is tangent to the curve

C and has the direction in which the

parameter

q (as well as the curvilinear abscissa) increases; the unit vector

is along

the principal normal and is directed towards the interior of the curve; the unit vector

is along the binormal and is directed so that the scalar triple product

(, , ) 0>τνβ (to

have a right-handed trihedron) (Fig.4.4).

Figure 4.4. Frenet’s trihedron.

Taking into account (4.1.8) and noting that

dr has the direction of the tangent to the

curve

C at the point P , we get

()

() ()

xqxq

′

== =

′′

(4.1.9)

Statics

207

Noting that the derivative of a vector of constant modulus is normal to it and that the

unit vector

τ is contained in the osculating plane to the curve at the point P , we may

write

()

s ρ

′

ν ;

(4.1.10)

the scalar

1/ 0ρ > is the curvature of the curve at the point

, while ρ is the radius

of curvature (the radius of the osculating circle to the curve at the very same point

We have thus

(d / d ) 0s⋅=ββ , because

, while the orthogonality relation

0⋅=τβ leads to (d /d ) 0s⋅=τβ , where we took into account the relation (4.1.10)

and the condition of orthogonality

⋅

β . We may write

()

s ρ

′

ν ;

(4.1.10')

the scalar

1/ ρ

′

is the torsion of the curve at the point P , while ρ

′

is the radius of

torsion at the very same point. Differentiating

βτ with respect to the curvilinear

abscissa

s and taking into account (4.1.10), (4.1.10'), as well as the vector products

=×τνβ and =×βτν, we may write

d11

()

s ρρ

′

==−−

′

(4.1.10'')

The formulae (4.1.10)-(4.1.10'') are called Frenet’s formulae (sometimes, the Serret-

Frenet formulae).

Starting from the formula (4.1.10), we get

(1/ ) (1/ ) (d / d )sρρ

==×

νβττ;

taking into account (4.1.9) and the modulus in both members, we obtain

() () d d

′′′

=× = ×rr rr

(4.1.11)

The scalar product of the relation (4.1.10'') by

, leads to 1/ (d / d )sρ

′

−⋅βν ;

taking into account (4.1.10), we may compute

()s

′

, while the vector product

=×βτν

leads to two mixed products, one of which vanishes. Using once more the

relation (4.1.10), as well as the relation (4.1.11), we may write

()( )

(), (), () (), (), ()ss s s s sρρ

′ ′′ ′ ′′ ′′′

=− =−

′

rr rττ τ

()

[]

(

)

()

d,d ,d

(), (), ()

() ()

ss s

′ ′′ ′′′

=− =−

′′′

rrr

rr r

(4.1.12)

MECHANICAL SYSTEMS, CLASSICAL MODELS

208

1.1.4 Geometry of a surface. Darboux’s trihedron

Let be a surface S , defined by the parametric equations

(,)

xxuv= , (,)uv D

∈

, 1, 2, 3j

(4.1.13)

where

()

xCD∈ , D being a given two-dimensional domain; a point P is specified

by the position vector

(,) (,)

uv x uv

ri, where u and v are curvilinear co-

ordinates on the surface (Fig.4.5,a). If one or the other one of the two curvilinear co-

ordinates is constant, then one obtains two families of co-ordinate lines

Figure 4.5. Co-ordinate lines on a surface (a). Darboux’s trihedron (b).

(, )uv=rr ,

(,)uv

rr ,

,constuv

(4.1.14)

where the vectors

d/d

′

=rr, d/d

′

rr have the same directions as the tangents

to these curves. Through a point

(

)

,uv of this surface passes only one co-ordinate

line of each family. The directions specified by the derivatives

′

r ,

′

r are distinct if

′′

×≠

rr 0, and the parametric representation (4.1.13) effectively defines a surface. In

this case, if

′′

⋅=

, then the co-ordinate lines form an orthogonal system. The

vectors

′

r and

′

r define the tangent plane to the surface at the point

(

)

,uv . A point

(

)

,uv which is an ordinary point for each of the two co-ordinate lines passing

through it and for which the condition

′

≠rr 0 holds is called an ordinary point of

the surface; a point which is not ordinary is called singular.

In this case too, we introduce a local system of reference (a movable frame), that is

the intrinsic Darboux’s trihedron (called also the Darboux-Ribaucourt trihedron); the

unit vectors of the co-ordinate axes of this three-orthogonal trihedron are defined as

follows: the unit vector

τ is tangent to a curve C on the surface and is directed so that

its curvilinear abscissa increases; the unit vector

is along the tangential normal

(normal to

, belonging to the tangent plane to

); the unit vector n is

along the normal to the surface, its direction being so that

(

)

,, 0

′

rrn . The

Statics

209

direction of the unit vector

is chosen so that the trihedron be right-handed

(

)

,, 0>gnτ ) (Fig.4.5,b). We suppose that P is an ordinary point.

If we introduce the mappings

()tut→ , ()tvt→ ,

[

]

,ttt

∈

, then the point P

describes a curve

C on the surface S ; the tangent to this curve is given by

ddd

′′

=+rr r . Starting from

dd d ds⋅= =rr r , we may write the element of

arc in the form

22 2

dd2dddsEu FuvGv=+ +,

(4.1.15)

where

′

= r ,

′

⋅rr,

′

= r ;

(4.1.15')

this expression represents the first basic quadratic form of the surface and was

introduced by Gauss. Taking into account Lagrange’s identity (2.1.33) and noting that

is an ordinary point, we find the condition

()

HEGF

′′

=× = −>rr

;

(4.1.15'')

hence, this quadratic form is positive definite in all the ordinary points of the surface.

The properties of a surface

S which depend only on the coefficients of the first

quadratic form (and of the partial derivatives of these coefficients) are called intrinsic

properties of the surface.

The element of area, that is the area of the curvilinear parallelogram obtained with

the vectors

′

r and d

′

r , is given by

ddddd

SuvHuv

′

=× =

rr .

(4.1.16)

We notice that the tangents to all the curves passing through

P are contained in the

plane defined by

′

r and

′

r ; the unit vector n of the normal to the surface at the point

mentioned above is – in this case – given by

1dd

uv uv

′′

′′ ′′

==×=×

′′

nrrrr

(4.1.17)

its direction being specified by

(

)

,, 0

′

rrn .

Projecting the first formula of Frenet (4.1.10) on the unit vector

n , we get

22 2

cos

dd2dddsLu MuvNv

=+ +,

(4.1.18)

where

(,)θ = ) n ν , and