Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

160

With the aid of the radii of gyration (3.1.30), the formulae (3.1.113), (3.1.114)

become

22 2

ii d

ΔΔ

+ ,

(3.1.113')

22 22

iidd

′

+−,

(3.1.114')

the notations corresponding to those used above.

For the polar and the planar moments of inertia, respectively, we may write also the

formulae

IIMρ=+

(3.1.115)

II Md

ΠΠ

=+,

(3.1.115')

corresponding to theorems of Huygens-Steiner type, where

is the position vector of

C with respect to O , while d is the distance between the parallel planes Π and

Π .

The properties previously established can be adapted to those formulae too.

Analogously, for the products of inertia we obtain a theorem of Huygens-Steiner type of

the form

II Mdd

ΔΔ Δ Δ

′′

′

(3.1.113'')

where

Δ and Δ

′

are axes corresponding to orthogonal directions and which pass

through the point

O , while d and d

′

represent the co-ordinates of the centre of mass

C with respect to those axes. These products of inertia may be also negative, so that

for the central axes we cannot have minimal values. As well, starting from axes which

pass through

C , one can find axes parallel to latter ones for which 0I

ΔΔ

′

= ; in the

plane case, the locus of the pole

O which has this property is an equilateral hyperbola.

Analogously, if

xxρ=+

(obvious notations) and if we take into account the

characteristic property of the centre of mass, then the relation (3.1.81) leads to a

synthesis of the Huygens-Steiner theorem in the form

(

)

kjk lljk k

IIMρρδ ρρ=+ −

,1,2,3jk

(3.1.116)

or in the form

() () ( )

OCOC

+IIISSS;

(3.1.116')

hence, we may state

Theorem 3.1.5. The moment of inertia tensor of a mechanical system with respect to

the point

O is equal to the sum of a moment of inertia tensor of the same system with

respect to the centre of mass

C and the moment of inertia tensor of the centre of mass,

at which we consider concentrated the mass of the whole mechanical system, with

respect to the point

O .

Mass geometry. Displacements. Constraints

161

If we write the relation (3.1.116') for the poles

O and O

′

, respectively, and if we

subtract the two relations, then we obtain the relation

() () ( ) ( )

OCOC

′′

=+ −III ISSS S;

(3.1.117)

we put thus in evidence the variation of the moment of inertia tensor of a mechanical

system

S by passing from a pole O to a pole O

′

. Denoting by

′

ρ and

η the

components of the vectors

′

JJJG

, OC

JJG

and OO

′

JJJG

, respectively (

ρρη

′

), we may

write too

()

jjj

kjk lljk k kk lljk

IIM Mηηδ η η ρ η ρ η ρηδ

′

⎡

⎤

=+ − − + −

⎢

⎥

⎣

⎦

wherefrom

() () ( ) ( ; )

OCCO

OOOO

′′′

=+ −III JSSS SS

(3.1.117')

with

(;) (;)tr (;)

CO CO CO

OO OO OO

′′ ′

=−JJ J1SS SS SS ,

(3.1.117'')

where

()

(;) () ()

CO OC O

OO O

′′

=⊗JSSSS S S

(3.1.117''')

represents the symmetric part of the dyadic product of the two vectors.

In the case of a discrete mechanical system of particles

P of position vectors

r ,

1,2,...,in= , we may write the identity

222 2

ijj ii ijj ii

ij i ij i

mmr mr mmr m

⎛⎞

=+ =

⎜⎟

⎝⎠

∑∑ ∑ ∑∑ ∑

(

)

iji j ij i j

ij ij

mm mm r r−⋅+ +

∑∑ ∑∑

rr , ij> .

Denoting by

r the distance between the particles

P and

P (

ij j i

−rrr), we get

ijij

ij j

MI S m m r

−

=+ =

∑∑

;

(3.1.118)

in particular, if

OC≡ , then the central polar moment of inertia is given by

11 11

nn nn

ijij ijij

ij j i j

Immrmmr

−

=+ = = =

∑∑ ∑∑

(3.1.118')

MECHANICAL SYSTEMS, CLASSICAL MODELS

162

2. Displacements. Constraints

A mechanical system can be free or subjected to constraints (internal constraints or

constraints due to the interactions with other systems). We are thus led to a study of the

constraints, which is based on the notion of geometric displacement.

2.1 Displacements

We put into evidence the real, possible and virtual displacements, which play an

important rôle in the representation of constraints as well as in the study of equilibrium

and motion of the mechanical systems.

2.1.1 Real, possible and virtual displacements

Let

P be a point of a mechanical system S subjected to the action of a system of given

forces. We suppose that the displacement of the point

from the given position of

position vector

r (at the moment

) to a neighbouring position P

′

of position vector

′

rr r (at the moment dtt t

′

+ ) is a differential quantity, compatible

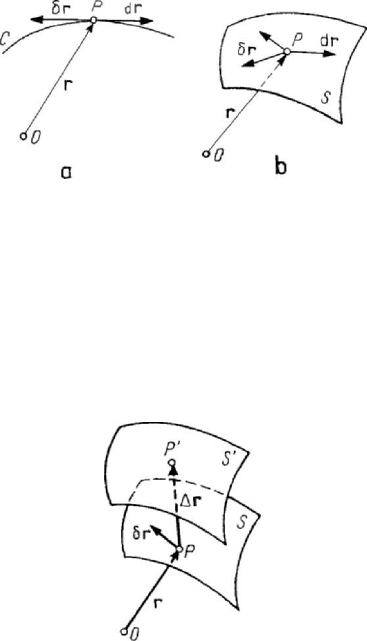
Figure 3.19. Real (a), possible and virtual (b) displacements.

with the constraints of the system (Fig.3.19,a). We call real displacement that one

which depends on the time

t and is determined by the forces acting upon the

mechanical system. The real displacement is univocally determined for a given system

of forces and for certain given conditions depending on the constraints of the

mechanical system; it corresponds to the real motion of the mechanical system,

supposing that the solution of the considered mechanical problem is unique. The

displacements

′

Δ= −

rr r, which depend on the time t and take place in a time

interval

tΔ , but which are not determined by the forces which act upon the mechanical

system, are called possible displacements; obviously, they are differential too and

compatible with the constraints of the system (sometimes, to be more specific, they are

called infinitesimal possible displacements). Possible displacements are all the

differential displacements which correspond to a possible position of a mechanical

system, at a given moment

t ; in general, they are not unique and can be also in an

infinite number. The real displacement is one of the possible displacements (it is

obtained if supplementary conditions are put to the latter ones, i.e., imposing the

dependence on the forces which act upon the mechanical system). By means of

relations

tΔ=Δrv, ddt

rv, (3.2.1)

Mass geometry. Displacements. Constraints

163

we may – analogously – introduce the possible velocities

v , to the set of which belongs

the real velocity

too. We notice that, in the case of a free mechanical system, any

displacement is a possible displacement and any velocity is a possible velocity.

Let

′

r and

′′

r be two possible displacements of the point P , which convey this

point to the neighbouring positions

′

and P

′

, respectively (Fig.3.19,b). We

introduce the differential displacement

r , which must be imposed to the point P , so

that this one do change its position from

′

to the neighbouring one P

′′

; this

displacement, equal to the difference of the two possible displacements

′

′′

=Δ −Δrrr

(3.2.2)

is called virtual displacement. Hence, by the summation of a possible displacement of a

point and a virtual one of the very same point, we obtain a new possible displacement

of the considered point. The relation (3.2.2) establishes a geometric link (and not a

kinematic one) between two possible displacements of a point

P and a virtual

displacement of the very same point; it gives thus the possibility of passage from a

possible displacement to another one. Thus, the virtual displacements (which are

differential quantities too) do not take place in time, but are compatible with the

constraints of the mechanical system at the time

t ; neither these displacements (as well

as the possible displacements) are not determined by the given forces. The virtual

displacements are thus displacements in the hypothesis in which the time

t is fixed

(the constraints of the system are “frozen”, hence they do not depend on time); this

point of view allows us to write – easily – constraint relations with the aid of virtual

displacements (differentiating the geometric constraints with the assumption that

constt = ). We notice that, although the virtual displacements do not take place in

time, they depend – in a certain manner – on this variable, because they are different

from a moment to another one; indeed, the virtual displacements represent the

displacements of the points of a mechanical system from a possible position at the

moment

t to a neighbouring possible position at the very same moment. In a stationary

case, the set of virtual displacements coincides with the set of possible displacements;

thus, fixing the time

t , we may pass from relations written by means of possible

displacements

Δr to relations expressed with the aid of virtual displacements δr .

Obviously, we admit that the virtual displacements

r are applied at the point P of

position vector

r , being – in fact – variations of this vector. V. Vâlcovici has

introduced the virtual displacements in the form

(

)

δ=Δ−Δ=Δ−Δrrv r

δ=Δ−Δ

(3.2.2')

where

v is the real velocity; the set of these displacements coincides with the set of the

displacements defined by the relation (3.2.2). From (3.2.1), (3.2.2), it follows that

∗

δ= Δrv

∗

′

′′

−vvv

;

(3.2.1')

we can thus introduce the virtual velocities

∗

v as a difference of possible velocities.

MECHANICAL SYSTEMS, CLASSICAL MODELS

164

For instance, in the case of a particle

P constrained to stay on a fixed curve C , the

real displacement

dr is tangent to the curve, having a specified direction; the possible

and the virtual displacements are also tangent to the curve, but can be oriented in any of

the two possible directions (there may exist two such displacements) (Fig.3.20,a). In the

case of a particle constrained to stay on a fixed surface

S , the real displacement dr is

tangent to the surface and univocally directed; but the possible and the virtual

displacements, the sets of which coincide (we are in a stationary case, as above), and

which are also tangent to the surface, can be anyone in the tangent plane (Fig.3.20,b).

If, besides the virtual displacement

r , there exists the virtual displacement −δr too,

then the virtual displacement is called reversible; otherwise, the virtual displacement is

called irreversible.

Figure 3.20. Real and virtual displacements on a fixed curve (a) or surface (b).

In both cases considered above, the curve and the surface are fixed, so that the real

displacement belongs to the set of virtual displacements. If a particle

P is, for instance,

on a movable rigid surface

S , the displacement of which is of translation velocity u ,

and if we introduce the relative velocities

′

and

′

, contained in the plane tangent to

the surface at the point

P , then we obtain the possible displacements

′′

Δ=Δ+Δrv u, tt

′

′′′

=Δ+Δrv u;

Figure 3.21. Real and virtual displacements on a movable rigid surface.

the virtual displacements of the form (3.2.1') thus obtained take place in the mentioned

tangent plane, at the moment

t . But the possible displacements connect points of the

surface

S to points of the surface S

′

(corresponding to the moment tt+Δ )

(Fig.3.21). Hence, in this case, the real displacement does not belong to the set of

Mass geometry. Displacements. Constraints

165

virtual displacements. In the case of a deformable surface, one may obtain analogous

conclusions.

2.1.2 Real and virtual work

Let

S be a mechanical system and

P points of it of position vectors

r ,

1,2,...,in= . The real elementary work of the forces

F , acting at the mentioned n

points of the system, is given by

=⋅

∑

Fr,

(3.2.3)

where we used the definition formula (A.1.28'); analogously, we introduce the virtual

work (the specification “elementary” is not necessary)

=⋅δ

∑

Fr.

(3.2.3')

For internal forces which verify the relation (1.1.81), we may write (Fig.1.18)

(

)

(

)

dd dd dd

ijijij ijji ijiij ji ij ij

Fr r⋅+⋅ = + ⋅+⋅ = ⋅ + =FrFr FF rFr u uu d

ij ij

Fr,

where vers

ur, while

ij ji

are positive quantities, in the case of repulsive

forces (which have the tendency to move off the points

and

P one of the other), or

negative ones, in the case of attractive forces; one obtains thus the real elementary work

of internal forces in the remarkable form

int

11 11

ddd

nn nn

ij ij ij ij

ij j i j

WFrFr

−

=+ = = =

∑∑ ∑∑

, ij

≠

(3.2.4)

Figure 3.22. Real work along a curve C .

Noting that

r ≷ for 0

F ≷ , it results that the real elementary work of internal

forces is a strict positive quantity (

int

d0W > ). In the case of a non-deformable

mechanical system (discrete non-deformable system or rigid solid) and only in the case

of such a system, we have

, so that

int

d0W

. In general, we can state that

int

dW is a non-negative quantity.

MECHANICAL SYSTEMS, CLASSICAL MODELS

166

In the case of a force

F , the point P of application of which describes a curve C

between the points

P and

P , we may write (Fig.3.22)

⋅

∫

Fr;

(3.2.5)

if the force is conservative, of the form (1.1.82), then we obtain

ddWU

(

)

(

)

()

WUPUPUU=−=−rr,

(3.2.5')

the real work depending only on the extreme positions of the point

. In the case of a

closed curve

, we have

⋅=

∫

(3.2.5'')

and the corresponding real work vanishes.

If there exists a function

U so that

ij ij ij

UFr

(3.2.6)

(for instance, if the internal forces depend only on the distances,

(

)

ij ij ij

FFr= , then

(

)

ij ij ij ij

UFrr=

∫

), then there exists the potential

11 11

nn nn

ij ij

ij j i j

UU U

−

=+ = = =

∑∑ ∑∑

≠

(3.2.6')

too, and the mechanical system is conservative. Thus, the elastic solids in adiabatic or

isothermic regime as well as the compressible fluids, in certain conditions (e.g., the

perfect gases), are conservative mechanical systems.

2.2 Constraints

In the following, we deal with the notion of constraint, which will be characterized

from a geometric, as well as from a kinematic point of view and for which we put in

evidence various classifications. A special attention is given to ideal constraints and to

constraints with friction, as well as to the constraints of a rigid solid; the constraint

forces which arise are thus put into evidence.

2.2.1 Classification of constraints. Axiom of liberation from constraints

A mechanical system (discrete or continuous) can be free or can be subjected to

some restrictions of geometric or kinematic nature; these restrictions, which represent a

limitation of the positions of the points of the system, will be expressed by relations

between the co-ordinates, or between the co-ordinates and the displacements

(velocities) of the respective points. We say that the mechanical system is subjected to

Mass geometry. Displacements. Constraints

167

constraints, which can be due to internal causes (internal constraints) or may be due to

interactions with other systems (external constraints). The constraints can be unilateral

(if, for instance in

E , a point P of the mechanical system is in one part with respect

to a surface

S or on the respective surface), being mathematically expressed by

inequalities (strict, if the point

P cannot belong to the surface, or not, otherwise), or

can be bilateral (if the point

P is on the surface S ), being expressed by equalities. As

well, the constraints can be of contact (if the mechanical systems – for instance,

continuous – are lying one on the other) or at distance (if the distance between two

points is invariant in time or depends on a certain law). Another classification of the

constraints puts into evidence the finite constraints (holonomic, of geometric nature)

and the infinitesimal (differential) constraints, of kinematic nature (in general, non-

holonomic); thus, we reach a mathematical representation of the constraints. We notice

also another classification, very important from the point of view of computation, i.e.:

ideal constraints (perfect, smooth) and constraints with friction (real); analytical

mechanics was developed just for mechanical systems subjected to ideal constraints.

The constraints which do not change in time (do not depend explicitly on time) are

called stationary (scleronomic) constraints; the constraints which vary in time are

called non-stationary (rheonomic) constraints. We mention also the critical constraints;

such constraints allow infinitesimal displacements which have not any correspondence

in finite displacements.

We can pass from the study of a mechanical system with constraints to the study of a

free one, using the axiom of liberation from constraints. This axiom allows us to

replace the constraints by constraint forces applied to certain points of the mechanical

system; in this case, the system may be considered as being free, but subjected to the

action of constraint forces too. We are thus led to a new classification of the forces, i.e.:

given (known) forces and constraint (unknown) forces; this classification is

independent of the previous classifications (in external and internal forces or in

conservative and non-conservative ones).

In these conditions, we may consider that the formulae (3.2.3), (3.2.3') give the real

elementary work and the virtual work of the given forces, respectively. Analogously, the

real elementary work of the constraint forces

R (the letter R corresponds to the word

“reaction”), applied at the same points

P , is expressed in the form

=⋅

∑

Rr,

(3.2.7)

while the corresponding virtual work is given by

=⋅δ

∑

(3.2.7')

In the case of internal constraint forces (corresponding to internal constraints and

verifying relations of the form (1.1.81) and (2.2.50)) one can establish a formula of the

form (3.2.4) for the corresponding work

MECHANICAL SYSTEMS, CLASSICAL MODELS

168

int

11 11

ddd

nn nn

ij ij ij ij

ij j i j

WRrRr

−

=+ = = =

∑∑ ∑∑

, ij

≠

(3.2.4')

The external constraint forces correspond to external constraints.

2.2.2 Geometric characterization of constraints

In an inertial frame of reference, the finite constraints of geometric nature are

expressed by relations between the position vectors of the points of the mechanical

system

S and the time t . In the case of a discrete mechanical system of n particles

P of position vectors

r , 1,2,...,in

, we may write these relations in the form (we

introduce a shortened notation, so that

r represents the set of all position vectors)

(

)

()

;,,...,;0

tf t≡=rrrr, 1,2,...,lp

(3.2.8)

where

is the number of the respective constraints; thus, the mechanical system

cannot occupy any position in the space, but only the positions allowed by the

restrictions (3.2.8). We suppose that the functions

are of the class

C , so that all p

constraints be distinct (no one of the constraints can be a consequence of the other ones

or of the differential equations of motion). We notice that

3pn

, so that the motion

may take place; the difference

3snp

− represents the number of geometric degrees

of freedom of the mechanical system S. If

3pn

, then the mechanical system has not

any geometric degree of freedom, being at rest with respect to the considered frame of

reference; solving a system of

3n equations with 3n unknowns (the co-ordinates of

the

n particles), one obtains the position of the mechanical system (eventually, this

position is not univocally determinate). We cannot have

3pn> , because in such a

case the constraints are no more distinct. In the above considerations, we have admitted

tacitly that the constraints are bilateral, in any expression being involved all the

particles of the mechanical system

S ; so that we can no more make considerations for

each particle (point of the mechanical system), as in the case of a single particle. In the

case of unilateral constraints of geometric nature of a mechanical system

S, we are led

to relations of the form

(

)

t ≥r , 1,2,...,lp

(3.2.8')

If the equality cannot take place for one of the constraints, then the respective

constraint is called strict. Obviously, the condition

3pn

must further hold.

We introduce the notations

()

3( 1)

−+

= , 1,2,...,in

, 1, 2, 3j

(3.2.9)

where

()

x are the components of the position vectors

r ; we may thus pass from the

geometric support

Ω of the discrete mechanical system S in the space

E (formed by

Mass geometry. Displacements. Constraints

169

the geometric points

P ) to a representative geometric point P (of generalized co-

ordinates

12 3

, ,...,

XX X ) in a representative space

E . The relations (3.2.8), which

express bilateral constraints, will be written in the form

(

)

()

12 3

; , ,..., ; 0

Xt fXX X t≡=, 1,2,...,lp

(3.2.8'')

while the relations (3.2.8'), corresponding to unilateral constraints, will take the form

(

)

Xt≥

1,2,...,lp

(3.2.8''')

The relations (3.2.8'') represent thus the conditions that the representative point

P be at

the intersection of

p hypersurfaces in the representative space

E , hence on a

manifold of dimension

3snp

− (equal to the number of geometric degrees of

freedom) of this space. Analogously, the relations (3.2.8''') represent the conditions that

the representative point

be only in one side of this manifold or, eventually, on the

manifold itself, if the constraint is not strict.

For instance, if a particle

can be only in the interior of a sphere of variable radius

Rvt− (v is a velocity), we impose the condition (we take the origin

at the centre

of the sphere)

()

(

)

222

123

0Rvt x x x−−++>.

(3.2.10)

If the mechanical system

S is formed by the particles

P and

P , linked by an

inextensible thread of length

l , then we impose the condition

() ()

()

() ()

()

() ()

()

222

12 12 12

11 22 33

0lxxxxxx

−

−−−−−≥;

(3.2.10')

denoting

()

Xx= ,

()

Xx= ,

()

Xx= ,

()

Xx= ,

()

Xx= ,

()

Xx= , the

representative point

P must be in a part of the hyperquadric (which corresponds to the

equality)

(

)

()

2 222222

1234 6 142 36

20l XXXXXX XXXXXX− +++++ + + + ≥

(3.2.10'')

or even on this one.

2.2.3 Degrees of freedom of a non-deformable mechanical system. Euler’s angles

Let

S be a discrete mechanical system of n free particles

P , 1,2,...,in= . The

position of a particle is determined by three arbitrary parameters (for instance, its co-

ordinates); we say, as in the previous subsection, that the system

S has

degrees of

freedom, because there are

3n necessary arbitrary parameters to determine its position.

If the discrete mechanical system is non-deformable (between the particles take place

geometric constraints (finite internal constraints), which maintain invariant the mutual

distances), then we notice that for

it has 3 degrees of freedom, for 2n = it has