Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

350

λ =± ,

(5.3.34')

Figure 5.35. Gear wheels with concurrent rotation axes.

where

n and

n represent the number of rotations per unit time. In the case in which

the rotation axes are concurrent, the wheels are truncated cones of vertex angles

and

α (Fig.5.35), respectively, and we get

sin

ωα

==± ;

(5.3.35)

if we have to do with trains of gears, then

R and

R of the formula (5.3.34) are the

radii of the two centrodes, and the formula may be written also in the form given by

Willis

==±,

(5.3.34'')

where

represent the number of teeth of the two wheels, respectively. We

mention also the trains of gear rack wheels, as well as the helical gear wheels (for

which the rotation axes have arbitrary relative positions). A more complex character

have the planetary and differential trains of gears. We mention also the worm-spiral

wheel trains (endless screw-helical wheel trains).

Figure 5.36. Mechanisms with flexible elements (a); using of crossed belts.

The mechanisms with flexible elements may use belts, cables, chains etc. In this

case, the direction of rotation is maintained (Fig.5.36,a); the direction may be changed

Kinematics

351

if crossed belts are used (Fig.5.36,b). The formulae (5.3.34), (5.3.34,b) remain still

valid.

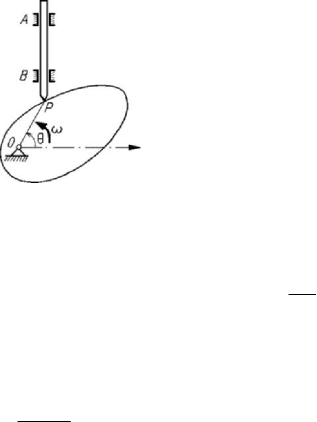
Figure 5.37. Cam gears.

The cam gears are used to transform the motions. The cam plays the rôle of a leading

element, having the pole

fixed, while the draw bar AB is the follower,

being

the point of contact (Fig.5.37). The point

P is moving after the law

()OP r f t==

where

()

t is a periodic function; if the cam has a rotation of angle

tθω θ=+, then

the shape of the cam is expressed in polar co-ordinates in the form

(

)

θθ

−

= .

(5.3.36)

Chapter 6

DYNAMICS OF THE PARTICLE WITH RESPECT TO

AN INERTIAL FRAME OF REFERENCE

Dynamics deals with the motion of mechanical systems subjected to the action of

given forces. We begin this study with a single particle in motion with respect to an

inertial frame of reference; as it was shown in Chap. 1, Subsec. 1.1.4, it is the frame

with respect to which the basic laws of mechanics are verified. If these laws hold with

respect to a certain frame, in a Newtonian model, then they are verified in any other

frame in rectilinear and uniform motion with respect to the first one, obtaining thus a set

of inertial frames of reference. To study the motion in such a frame, we emphasize the

corresponding general theorems, both for the free and the constraint (frictionless or

with friction) particle.

1. Introductory notions. General theorems

After introducing mechanical quantities which play an essential rôle in the frame of

the Newtonian model, we formulate the problem of the free particle, emphasizing the

methods of solving it; the theorems of existence and uniqueness are thus presented and

stress is put on the notion of first integral. The principle of relativity allows to establish

the Galileo-Newton transformations group. Starting from the general theorems

corresponding to the motion of the particle, one obtains the conservation theorems,

hence the first integrals of the equations of motion; the first integral of areas leads then

to the notion of central force.

1.1 Introductory notions

In what follows, we introduce the notions of momentum, moment of momentum,

work, kinetic and potential energy, power and mechanical efficiency; the conservative

and non-conservative forces are then considered. We mention also the formulation of

the problem of the free particle in motion and the presentation of the equations of

motion in curvilinear co-ordinates.

1.1.1 Momentum. Moment of momentum. Torsor of momentum

We have introduced the notion of momentum in Chap. 1, Subsec. 1.1.6; thus the

momentum (linear momentum) of a particle

of position vector r with respect to a

given fixed frame of reference (which is supposed to be inertial), is expressed in the

form

35 3

MECHANICAL SYSTEMS, CLASSICAL MODELS

354



Hvr

(6.1.1)

and is a vector collinear with the velocity

of the respective particle.

The moment of the momentum with respect to the pole

O of the frame of reference

is called moment of momentum (angular momentum) of the particle, with respect to this

pole, and is given by

mm m=×=×=×=



KrHrv rr , (6.1.2)

where we have introduced the areal velocity (5.1.16). In general, we may consider a

moment of momentum with respect to any given fixed point (fixed with respect to an

inertial frame of reference).

In components, we have

iii

Hmvmx

=  , 2

Oi Oi ijk k

Km mxxΩ

=∈  ,

1, 2, 3i

. (6.1.3)

The notion of torsor, introduced in Chap. 2, Subsec. 2.1.3, allows to write

{

}

() ,

=HHK;

(6.1.4)

hence, the set formed by the linear and angular momentum of a particle represents the

torsor of the momentum of the respective particle with respect to the considered pole.

We notice that the torsor (6.1.4) may be obtained from the torsor (5.1.16') multiplying it

by the mass

m . The notion of torsor plays thus – in the problems of dynamics – a rôle

analogous to that performed in statics.

1.1.2 Work. Kinetic and potential energy. Conservative forces

The notion of work (mechanical work) has been introduced in Chap. 3, Subsec.

2.1.2, in the form of real elementary work (3.2.3); considering only real displacements,

we may omit the adjective “real” in what follows. In this case, the elementary work of

the given forces is of the form

ddd

WFx

⋅=Fr , (6.1.5)

where

is the resultant of the given forces which act upon the particle

, which

effects a real displacement

; analogously, the elementary work of the constraint

forces is given by

ddd

WRx

⋅=Rr , (6.1.5')

where

R is the resultant of the constraint forces applied at the point P . Using the

property of distributivity of the scalar product with respect to the addition of vectors, it

results that the elementary work of a resultant force is equal to the sum of the

elementary works of the component forces which act upon the same particle. The same

property allows us to state that the elementary work of a resultant displacement

is equal to the sum of the elementary works corresponding to successive component

Dynamics of the particle with respect to an inertial frame of reference

355

displacements; in this case, if the particle

P describes a trajectory C between the

points

P and

P , the work of the given force is expressed by





01 01

PP PP

WFx=⋅=

∫∫

Fr .

(6.1.6)

The work is a scalar quantity, expressed in ergs in the CGS-system or in joules in the

SI-system (see also Table 1.1).

We notice that we may express the elementary work in the form

dddprprdWtrF=⋅ = =

Fv F r

(6.1.5'')

too, obtaining – in general – a Pfaff form (it is not an exact differential).

The given force may be of the form

(,;)t



FFrr

; if we know the trajectory

()t=rr, then the elementary work depends only on time, and the curvilinear integral

(6.1.6) becomes a simple one. If the position of the particle and the force

are

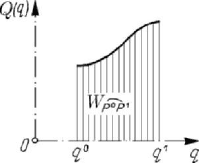
specified by a parameter

( ()q

rr , ()q

FF ), then

d () ()d () ()d ()d

W q qq Fqxqq Qqq

′

=⋅ = =Fr

(6.1.5''')

Figure 6.1. Work diagram.

and the work of the given forces is expressed with the aid of a simple integral too; in

this case, we may introduce the work diagram (Fig.6.1), sometimes useful in practice. If

the force

F depends only on the position of the particle ( (;)t

FFr), then the work

depends only on the trajectory and is independent on the velocity by which that one is

travelled through.

In the case of a conservative force

F (which derives from a simple potential, being

of the form

gradU=F

, ()UU

r , the elementary work becomes an exact

differential

ddWU

, (6.1.7)

the work

W depending only on the extreme positions of the particle

(



() ()

WUU=−rr). If the trajectory C is a closed curve, then the

corresponding work vanishes (

MECHANICAL SYSTEMS, CLASSICAL MODELS

356

In the case of a quasi-conservative force, which derives from a simple quasi-

potential

(;)UU t= r , the elementary work is no more an exact differential, but is of

the form

dgraddd dWU UUt=⋅=−



r ,

(6.1.8)

where we emphasized the partial derivative with respect to time.

In Chap. 1, Subsec. 1.1.12, we have introduced the generalized potential

00jj

UUUvU=⋅+ = +Uv , (6.1.9)

where

()UU

r and ()UU

r are scalar and vector potentials, respectively. The

components of the conservative force, defined by means of this potential, are of the

form

[

]

, 1, 2, 3j

, (6.1.10)

where we have put in evidence the Euler-Lagrange derivative, corresponding to the

index

j , given by

[]

∂

⎛⎞

=−

⎜⎟

∂

⎝⎠



;

(6.1.10')

this derivative corresponds to the formula (1.1.88) and allows to express these

components by a formula analogous to (1.1.82). Taking into account (6.1.9) and noting

that

∂

∂∂

we obtain

()

grad grad

=−= ⋅+−

FUv

(6.1.11)

Replacing the vector potential U by the vector potential

gradϕ=+UU

, ()ϕϕ= r ,

and taking into account the relation

d/d gradtϕϕ

⋅v , as well as that one may

invert the order of application of the operators (

grad(d / d ) (d/ d )gradtt

) for a

function

ϕ of class

C , we find the same force F ; hence, the vector potential is

determined abstraction of a field of gradients. The velocity

being a function only on

time, the formula (A.2.31) allows us to write

grad( ) ( ) curl curl

⋅=⋅∇+× = +×

UvvUvU vU

;

Dynamics of the particle with respect to an inertial frame of reference

357

taking into account (6.1.9), we may express the conservative force

F in the form

(

)

00,

grad curl

kj jk k

UUUvU=+×=−+

⎡

⎤

⎣

⎦

FvU i

(6.1.11')

The above observation concerning the transformation of a vector potential

→UU is

easily verified (

curl gradϕ

0 ).

In the case of a generalized quasi-potential, the two quasi-potentials are of the form

(;)UU t= r and (;)t=UUr, respectively; the expression (6.1.11) of the quasi-

conservative force remains still valid. Noting that

d/d ( )t

⋅∇ +



UvUU, where the

point indicates the partial derivative with respect to time, we may express the force

in the form

grad curlU=+×−



FvUU.

(6.1.11'')

If to the transformation of vector quasi-potential

→UU, considered above, we

associate the transformation of scalar quasi-potential

000

UUUϕ→=+ , hence if we

effect the transformation

d/dUUU tϕ→=+

, then the form (6.1.11) (or the form

(6.1.11')) of the quasi-conservative force remains invariant; that is a gauge

transformation.

In the case of a conservative force which derives from a generalized potential, the

elementary work is given by

ddgradd(,curl,d)WU=⋅ = ⋅ +Fr r v Ur,

hence it is a total differential

ddWU

. (6.1.12)

Thus, the formulae (6.1.11') and (6.1.12) show that the scalar potential

plays the

rôle of the simple potential in the frame of the generalized potential (6.1.9), and the

vector potential has no contribution in what concerns the elementary work; all the

considerations made for the simple potential remain still valid. If the force is quasi-

conservative, deriving from a generalized quasi-potential, we obtain

00 0 0

dd d dd( )dWUUt U Ut=−−⋅=−⋅+



Ur Uv

(

)

00,

(grad ) d d

UUUx=−⋅=−



Ur ;

(6.1.12')

one can easily see that the gauge transformation mentioned above has not one influence

on this elementary work too.

We notice also that a conservative force derives always from a generalized or a

simple potential as it depends or not explicitly on the velocity of the particle.

The notion of work appeared in XIXth century with the occasion of experiments

concerning the transformation of mechanical motion into heat (a non-mechanical form

MECHANICAL SYSTEMS, CLASSICAL MODELS

358

of motion of the matter); one observes that in this transformation there is a constant

ratio between the effected work and the obtained heat. The work represents thus a

measure of the mechanical motion of a particle, which is transformed in a non-

mechanical motion of it.

As well, the work allows a dynamic measurement of the action of a force. The

positive work is a motive work

W , which puts the particle in motion, while the

negative work is a resistent work

W for which it is necessary to use up external

energy. The work vanishes if the force or the displacement vanish or if they are

perpendicular one to the other.

We notice that one may use a quantity of state to characterize the mechanical motion

of a particle. Indeed, taking into account Newton’s basic law (1.1.89''), we have,

successively,

ddd

dd()d d dd

ddd

W mmmm

ttt

=⋅ = ⋅ = ⋅ = ⋅ = ⋅

Fr v r r v vv

(

)

(

)

d1 d1

d2 d2

mmvT

===v

introducing the scalar quantity

Tm mv==v

(6.1.13)

called kinetic energy of the particle

P ; this quantity depends on the mass and the

velocity of the particle. Taking into account the above considerations concerning the

work, it follows that the kinetic energy is a quantity of state of the particle, which

measures its mechanical motion and its capacity to be transformed into a non-

mechanical motion.

Taking into account the modality of introducing the kinetic energy, we notice that

the simple potential

U (or the scalar potential

U ) is a quantity of energetical nature;

hence, we introduce the function

−

(6.1.14)

−

, (6.1.14')

where

()VV

r is called potential energy.

The sum

ETV

(6.1.15)

is called total mechanical energy (or mechanical energy).

Dynamics of the particle with respect to an inertial frame of reference

359

1.1.3 Power. Mechanical efficiency. Power of non-conservative forces

The quantity

(6.1.16)

is called power (mechanical power) and is measured in erg/s in the CGS-system or in

J/s=W in the SI-system (see Table 1.1); in practice, 1 HP=75 kgf · m/s (HP means

horse-power) is used too. Taking into account (6.1.5), we may also write

⋅=⋅

FFv

(6.1.16')

This quantity is used to the calibration of motors, engines, apparatuses etc.

Assuming that an engine may be modelled as a particle, the motive work is equal to

the resistent one (

WW= ), in a regime working of it; here and in what follows we

consider the work in absolute value (always positive). We notice that the resistent work

is formed by the useful work

W , realized by the engine for the goal for which it was

built up, and by the passive (lost) work

, used up by the passive forces (frictions,

various resistent forces etc.); we have thus

mup

WWW

, the engine playing the

rôle of a transformer of work. To the motive, the useful and the passive work

correspond the motive power

P , the useful power

P and the passive power

(

mup

PPP=+

), respectively, taken – in what follows – also in absolute value (always

positive).

We call mechanical efficiency the ratio

111

mmmm

WWPP

η ==−==−<

(6.1.17)

which is always subunitary (if not, the engine would be a “perpetuum mobile”), being a

transfer function of the power; the ratio

pm pm

WW PP

put in evidence is the loss

factor.

If we introduce the force transmission factor and the velocity transmission factor

(used in Chap. 5, Subsec. 3.3.3) by relations

λ = ,

(6.1.18)

where

and

are the components of the velocity (in modulus) along the direction

of the motive force

F and of the useful force

F , respectively, we may write

umm

muu

PFv

ηλ λ = ;

noting that

mmm

PFv= and

uuu

PFv

, we get

MECHANICAL SYSTEMS, CLASSICAL MODELS

360

Theorem 6.1.1 (the black box law). The product of the force transmission factor by the

velocity transmission factor and by the mechanical efficiency of an engine is equal to

unity

λλη

. (6.1.19)

Because the transmission factors may be obtained experimentally, this law determines

the mechanical efficiency, so that it is not necessary to disassemble the engine for this (as

it would be in the interior of a black box). In the case of an ideal engine (for which

1η = ,

the friction being so small that it can be neglected), we obtain

λλ

; (6.1.19')

in this case, the force transmission factor is the inverse of the velocity transmission

factor.

Figure 6.2. Case of inclined plane.

For instance, in the case of the inclined plane (which makes an angle

α with the

horizontal line (Fig.6.2)) with friction (coefficient of sliding friction

tan

ϕ= ),

considered in Chap. 4, Subsec. 2.1.6, which allows to move up a rigid solid (modelled

by a material point

P ), of weight G , with the aid of a force F (which makes the angle

with the inclined plane), we have (

, cos

vvβ

, sin

vvα= )

1sin

cos

λλ β

;

if the inclined plane is used to move up a rigid solid, then we use the relation (4.2.13)

and obtain the mechanical efficiency

sin cos( ) sin (cos sin )

1tan

cos sin( ) cos (sin cos ) 1 cot

αβϕ αβ β

βαϕ βα α α

−+

== =

+++

(6.1.20)

while if it is used to move down the heavy bodies, then the relation (4.2.14) leads to

sin cos( ) sin (cos sin )

1tan

cos sin( ) cos (sin cos ) 1 cot

αβϕ αβ β

βαϕ βα α α

+−

−

== =

−−−

(6.1.20')

0β = , then we obtain