Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

Dynamics of the particle with respect to an inertial frame of reference

381

where

consth

, hence to a scalar first integral. Introducing the potential energy

(6.1.14) or (6.1.14') and the mechanical energy (6.1.15), we may write

ETV h=+=, consth

(6.1.55'')

too, obtaining thus

Theorem 6.1.16 (mechanical energy conservation theorem). The mechanical energy of

a free particle is conserved in time if and only if the resultant of the given forces which

act upon it is conservative.

Thus, the denomination given to these forces, which form a conservative field, is

justified;

h is the energy constant.

The mechanical energy conservation theorem allows to determine the magnitude of

the velocity of the particle without knowing its trajectory; we may thus write

[]

()vhV

=−

r .

(6.1.56)

We notice that – in particular – the motion of a particle constrained to stay on an

equipotential surface and acted upon by the corresponding conservative force is

uniform.

The constants corresponding to the first integrals introduced above may be

determined observing that the latter ones are conserved in time (the respective functions

have the same value at any moment

t , inclusive at the initial moment

tt= ). Thus, in

the case of the linear momentum conservation theorem it results

Cv, in the case

of the angular momentum conservation theorem we have

()m=×Cr v, while in

the case of the mechanical energy conservation theorem we may write

/2 ( )hmv V=+r .

1.2.6 Theorem of areas. Central forces

Starting from the velocities torsor (5.1.16'), multiplying by the mass m and taking

into account (6.1.1), (6.1.2), we find again the torsor of momentum (6.1.4); multiplying

– analogously – the accelerations torsor (5.1.20') by

m and taking into account

(6.1.45), (6.1.46'), we obtain the torsor theorem (6.1.47). We can thus see that the areal

velocity and acceleration play for the angular momentum and its derivative a rôle

similar to that played by the velocity and the acceleration for the linear momentum and

its derivative, respectively. Thus, if the force

F is coplanar (concurrent or parallel)

with an axis

Δ of unit vector

( 0M

), then the projection of the areal velocity

Ω of the free particle P on the axis Δ is constant in time

(, , )

iij

OOiijkk

uxvuCΩ⋅= = =∈ =urvuΩ ,

constC

(6.1.57)

obtaining a scalar first integral equivalent to (6.1.54); associating a particle

′

to the

projection of the particle

P on a plane Π normal to the axis Δ , we may state that the

MECHANICAL SYSTEMS, CLASSICAL MODELS

382

areal velocity of the particle

′

with respect to the trace of the axis Δ on the plane Π

is conserved in time. Assuming that the axis

Δ coincides with the axis

Ox , we may

write

()()

12 21 12 2 1

xv xv xx xx CΩ

−= −=

, constC

(6.1.57')

As well, if the moment

M has a fixed support, then we obtain two independent

scalar first integrals of the form (6.1.57). If the force

F is contained in a fixed plane

Π , then the trajectory of the particle P is a plane curve, while the moment of

momentum is of the form

()

Ku, where vers

uK is normal to the plane

Π ; one can easily see that

[

]

() () 0

mKt⋅=⋅× = ⋅=rK r r v ur ,

hence

0⋅=ur , so that this is the equation of the plane

, which passes through

The condition

=M0 is verified if and only if the support of the given force F

passes through the pole O ; such a force is called central force. In such a case, the

moment of momentum conservation theorem takes place; we also obtain

=×=rv CΩ , const=





C ,

Oi ijk k

xv CΩ =∈ = , 1, 2, 3i

, (6.1.57'')

hence, a vector first integral, equivalent to three scalar first integrals, and we may state

Theorem 6.1.17 (areal velocity conservation theorem). The areal velocity of a free

particle with respect to a fixed pole is conserved in time if and only if the resultant of

the given forces which act upon it is a central force (its support passes – permanently –

through the same pole).

In the latter case

(

)

(

)

1/2 ( , , ) 1/2

⋅= = ⋅rrvrCrΩ ; hence, the trajectory of the

particle

P is a plane curve, contained in the plane

0⋅=Cr , const

≠





C0,

(6.1.58)

which passes through the pole

O . If

C0, then it results that r and v are collinear

vectors; the equation

()tλ=



rr, λ scalar, leads to

()d

λτ τ

∫

rr ,

(6.1.58')

the trajectory of the particle being rectilinear. We notice that

=×Cr v. As a

conclusion, if the moment

M has a fixed support, then the trajectory of the particle

P is rectilinear or a plane curve (contained in the plane Π ) as the vectors

r and

of the initial conditions have or not the same support.

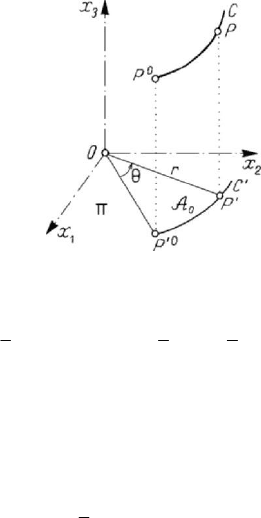
Dynamics of the particle with respect to an inertial frame of reference

383

Assuming that the plane

Π coincides with the plane

Ox x , the particle P

describes the curve

C , the trajectory of the particle P

′

being the curve C

′

, the

projection of the curve

C on the plane Π (Fig.6.5); if the trajectory C is a plane

curve, in the conditions mentioned above, then

′

≡

. We may write

Figure 6.5. Areas theorem.

()

12 21

111

222

xx xx r CΩθ=−==



 ,

(6.1.59)

where we used polar co-ordinates in the plane Π ; the first integral

rCθ =



is called

also the areas first integral. Noting that

d/d

tΩ

, where we have attached the

sign +, to the area

, corresponding to a positive rotation in the plane Π , we get

()

Ct t=−A ,

(6.1.59')

and are led to

Theorem 6.1.18 (areas theorem). The area described by the vector radius of a free

particle, beginning with its initial position, is proportional to the interval of time

covered if and only if the resultant of the given forces which act upon it is a central

force.

We can also say that the vector radius describes equal areas in equal times. The

constant

C is called the areas constant. We mention that this theorem has been stated

in the same conditions in which the areal velocity conservation theorem takes place; but

it can be applied to the particle

′

too (Fig.6.5), in the case in which we may write

only a single scalar first integral of the form (6.1.57).

Taking into account the observations made at the beginning of this subsection, the

angular momentum theorem allows to write

m =



MΩ

(6.1.60)

and we may state

MECHANICAL SYSTEMS, CLASSICAL MODELS

384

Theorem 6.1.19 (areal acceleration theorem). The product of the double mass of a free

particle by its areal acceleration with respect to a fixed pole is equal to the moment of

the resultant of the given forces which act upon it, with respect to the same pole.

Hence, the equation (6.1.60) plays – with respect to the moment

– the same rôle

as that played by Newton’s equation (1.1.89) with respect to the force

2. Dynamics of the particle subjected to constraints

Assuming that the particle is subjected to ideal constraints or to constraints with

friction, we complete – in what follows – the general and conservation theorems

previously stated and emphasize the differential principles of mechanics for a particle.

Using then the general results thus obtained, we study the motion of a particle

constrained to stay on a curve or on a surface; the case of constraints with friction is

also taken into consideration. By means of the generalized co-ordinates, we may study

the motion of a particle with only one degree of freedom in the conservative case, as

well as in a dissipative case.

2.1 General considerations

The case of one or two ideal holonomic (rheonomic or scleronomic) constraints is

considered and the equation of motion, the general and the conservation theorems are

completed by introducing the constraint forces. We mention also the presentation of

other differential principles of mechanics (d’Alembert, d’Alembert-Lagrange),

equivalent to Newton’s differential principle.

2.1.1 Ideal constraints. Introductory notions

We introduced in Chap. 3, Sec. 2.2 the notion of constraint, together with its multiple

implications. Using the considerations made on this occasion, we assume that a particle

may be subjected to two holonomic (finite, of geometric nature) bilateral constraints of

the form (3.2.17); if a third constraint, compatible with the first two ones, would appear,

then the position of the particle would be specified from geometric point of view

(uniqueness or not). The case of non-holonomic constraints of the form (4.1.37') will be

studied subsequently by analytical methods. As well, we admit the existence of

unilateral constraints of the form (3.2.8') in some particular problems.

If the particle is constrained to stay on a curve

C , then its co-ordinates must verify

the relations

(

)

1123

,,; 0

xxxt

(

)

2123

,,; 0

xxxt

(6.2.1)

or the relations

(

)

1123

,, 0

xxx

(

)

2123

,, 0

xxx

(6.2.1')

as the constraint is rheonomic or scleronomic, respectively; in the first case, the curve is

movable, while in the second one it is fixed. The particle remains with only one degree

Dynamics of the particle with respect to an inertial frame of reference

385

of freedom and its position may be specified by means of a single independent

parameter

q (obtained by eliminating the two considered constraints) in the form

(;)qt=rr , (;)

xxqt

, 1, 2, 3i

, ()qqt

(6.2.2)

in the general case of a rheonomic constraint. In particular, the generalized co-ordinate

may be the curvilinear co-ordinate s on the curve

or even the time

Analogously, to determine the positions of a particle constrained to stay on a surface

S of equation

(

)

123

,,; 0

xxxt

(6.2.3)

(

)

123

,, 0

xxx

(6.2.3')

as the constraint is non-stationary (movable surface) or stationary (fixed surface),

respectively, there are necessary two parameters

,qq (obtained by the elimination of

the considered constraint), corresponding to two degrees of freedom; it results

(, ;)qqt=rr ,

(, ;)

xxqqt= , 1, 2, 3i

, ()qqt

αα

, 1, 2α = .

(6.2.4)

The generalized co-ordinates

,qq, may – eventually – be the co-ordinates on the

surface

S .

Using the axiom of liberation from constraints, we introduce the constraint force

so that, corresponding to the formula (3.2.35'), the equation of motion (6.2.2) becomes

mm==+



arFR,

iiii

ma mx F R

=+ , 1, 2, 3i

; (6.2.5)

in such conditions, the particle behaves as a free one. If the constraints are ideal, then

one obtains the virtual work

=⋅δ=Rr

; in the cases considered above, the

constraint force

is normal to the surface

, hence it is of the form

grad

λ=R

,ii

Rfλ

1, 2, 3i

, λ scalar, (6.2.6)

or it belongs to the normal plane to the curve

C , hence it is of the form

1122

grad grad

fλλ=+R

11, 22,

Rf fλλ

+ , 1, 2, 3i

,λλ

scalars, (6.2.6')

at the point occupied by the particle (corresponding to the formula (3.2.37)). A

constraint with friction implies a constraint force tangent to the surface

S or to the

curve

C , which is determined by a supplementary modelling of the mechanical

phenomenon.

We observe that all the results obtained in the case of a free particle may be used also

for a particle subjected to constraints if to the resultant

F of the given forces is

MECHANICAL SYSTEMS, CLASSICAL MODELS

386

added also the resultant

R (unknown) of the constraint forces. In the first basic

problem, besides the trajectory (the vector function

()t

rr) is asked also the

constraint force

R (which involves – in general – three unknown scalar components).

In the second basic problem, one must determine the forces

F and R ; as in the case

=R0, the problem has not a unique solution. As well, neither in the case of the mixed

basic problem the solution is not unique.

In what concerns the theorem of existence and uniqueness, they remain further valid

if the functions (6.2.1') and (6.2.3') are of class

C and their derivatives of first order

fulfil conditions of Lipschitz type.

2.1.2 General theorems

Corresponding to the results in Subsec. 1.2.4, we may write



HFR,

iii

HFR



, 1, 2, 3i

(6.2.7)

()

OOO

=× + = +



KrFRMM,

Oi Oi Oi

KMM=+



, 1, 2, 3i

(6.2.7')

thus stating:

Theorem 6.2.1 (theorem of momentum). The derivative with respect to time of the

momentum of a particle subjected to constraints is equal to the resultant of the given

and constraint forces which act upon it.

Theorem 6.2.2 (theorem of moment of momentum). The derivative with respect to time

of the moment of momentum of a particle subjected to constraints, with respect to a

fixed pole, is equal to the moment of the resultant of the given and constraint forces

which act upon it, with respect to the same pole.

Introducing the notion of hodograph, we may state theorems analogous to Theorems

6.1.7' and 6.1.8'.

Noting that

() () ()

OOO

τ=τ+τ



HFR,

(6.2.7'')

we may state

Theorem 6.2.3 (theorem of torsor). The derivative with respect to time of the torsor of

momentum of a particle subjected to constraints, with respect to a fixed pole, is equal to

the torsor of the resultant of the given and constraint forces which act upon it, with

respect to the same pole.

Introducing the impulse of the constraint force

∫

R and the impulse of the

moment of the constraint force

∫

M , corresponding to the interval of time

[

]

,tt , we may write

ttΔ= +

∫∫

HF R,

(6.2.8)

OO O

ttΔ= +

∫∫

KM M,

(6.2.8')

Dynamics of the particle with respect to an inertial frame of reference

387

(

)

(

)

() d d

OO O

ttΔτ = τ + τ

∫∫

HF R

(6.2.8'')

The relation (6.1.48) is completed in the form

dd d d d

TWW=+ =⋅+⋅FrRr

(6.2.9)

and we may state

Theorem 6.2.4 (theorem of kinetic energy). The differential of the kinetic energy of a

particle subjected to constraints is equal to the sum of the elementary works of the

resultants of the given and constraint forces which act upon it.

As it was seen in Chap. 3, Subsec. 2.2.9, in the case of scleronomic (or – more

general – catastatic) constraints, we have

; in this case, the Theorem 6.2.4,

corresponding to a particle subjected to constraints, is of the same form as the Theorem

6.1.10, corresponding to a free particle. In what concerns Theorems 6.1.10' and 6.1.10'',

one can make analogous observations.

We notice that, if we take the moment of momentum with respect to a pole

Q ,

movable with respect to the origin

O , the formula (6.1.52) leads to

QQQQ

+−×



KMMvH

(6.2.10)

2.1.3 Conservation theorems

Using the results given in Subsec. 1.2.5, we may build up first integrals, in certain

conditions, in the case of a particle subjected to constraints too. Thus, if the sum

+FR

is parallel to a fixed plane (is normal to a fixed direction of unit vector u ,

()0+⋅=FRu ), then we may write the first integral (6.1.53); analogously, if the sum

+MM is contained in a fixed plane (is normal to a fixed axis Δ , O Δ∈ , of unit

vector

u ,

(

)

+⋅=MMu ), then one obtains the first integral (6.1.54).

+=FR 0 (necessary and sufficient condition of static equilibrium), then we

may state a momentum conservation theorem, while if

=MM 0 (necessary

condition of static equilibrium), then we may state a moment of momentum

conservation theorem. The first condition mentioned above allows to state a torsor

conservation theorem too.

In the case of scleronomic constraints and of a conservative force we may write also

a mechanical energy conservation theorem.

The moment of momentum conservation theorem is equivalent to the areal velocity

conservation theorem; these theorems take place if and only if the sum

+FR passes

through the fixed pole

O (it is a central force).

As in the case of a free particle, one can obtain only six independent first integrals;

but these ones are sufficient to determine the motion. Even if the constraint force

R is

not known a priori, the conditions imposed above are often fulfilled, and we may set up

first integrals in the case of the particle subjected to constraints too.

MECHANICAL SYSTEMS, CLASSICAL MODELS

388

2.1.4 Differential principles of mechanics

The equation of motion of a particle P subjected to constraints is written in the form

(6.2.5); this equation represents Newton’s principle (the first differential principle of

mechanics). But this basic principle can be expressed also in other equivalent forms,

which are useful in various particular cases; if we consider these forms as consequences

of Newton’s principle, then they will be theorems.

Introducing the force of inertia

−



Fr,

(6.2.11)

the law of motion becomes

+=FFR 0

(6.2.12)

Figure 6.6. D’Alembert’s theorems.

and we may state (Fig.6.6)

Theorem 6.2.5 (d’Alembert). The motion of a particle subjected to constraints takes

place so that – at any moment – it is in dynamic equilibrium under the action of the

resultant of the given and constraint forces, as well as of the force of inertia.

We introduce the force

+=−



FF F rΦ ,

(6.2.13)

which is called the lost force of d’Alembert; in this case, the equation becomes (Fig.6.6)

=R0

(6.2.14)

and we can state

Theorem 6.2.6 (d’Alembert). The motion of a particle subjected to constraints takes

place so that the constraint force be equilibrated – at any moment – by the lost force of

d’Alembert.

We notice that the relation (6.2.13) may be written also in the form

() m=+−=+



FF rΦΦ;

hence, only the component

−



rF of the force

contributes to the motion of the

particle, while the component

is lost because it equilibrates the constraint force

(justifying thus the given denomination).

Formally, the equation (6.2.14), which represents the necessary and sufficient

condition for dynamic equilibrium (characterizing – entirely – the motion of the particle

subjected to constraints), is not different from the relation (4.1.4), which represents the

Dynamics of the particle with respect to an inertial frame of reference

389

necessary and sufficient condition of static equilibrium. As a consequence, all the

considerations made for static problems, starting form the relation (4.1.4), may be

transposed for similar problems of dynamic character, replacing the given force

F by

the lost force of d’Alembert

; e.g., the condition (4.1.56), written for only one

particle, leads to the theorem of torsor, characterized by the formula (6.2.7''). As well,

we may use the results in Chap. 4, Subsecs. 1.1.5, 1.1.6, 1.1.8, corresponding to the

particle constrained to stay on a surface or on a curve.

Wδ=, then we may write the relation (4.1.58) for a single particle in the form

=⋅δ=r

, (6.2.15)

stating

Theorem 6.2.7 (theorem of virtual work; d’Alembert-Lagrange). The motion of a

particle subjected to ideal constraints takes place so that the virtual work of the lost

force of d’Alembert, which acts upon the particle, vanishes for any virtual displacement

of it.

In the case of unilateral ideal constraints of the form (3.2.16

) or of the form

(3.2.16), the virtual work of the lost force of d’Alembert verifies the relation

=⋅δ≤r

. (6.2.15')

We notice that each of the above theorems may stay at the basis of the Newtonian

mathematical model of mechanics, representing thus a differential principle of

mechanics.

2.2 Motion of the particle with one or two degrees of freedom

In what follows, we consider the motion of a particle (frictionless or with friction),

constrained to stay on a curve or on a surface. A study is then made for the case in

which the particle has only one degree of freedom (conservative or dissipative case).

2.2.1 Motion of a particle constrained to stay on a curve

Let P be a particle in motion on a smooth movable or fixed curve C (Fig.6.7) of

equations (6.2.1) or (6.2.1'). The constraint force will be expressed in the form (6.2.6'),

while the equation of motion will be

1122

grad gradmffλλ=+ +



rF ; (6.2.16)

in components, we may write

11, 22,

mx F f fλλ=+ + ,

1, 2, 3i

. (6.2.16')

The equations (6.2.1) and (6.2.16') form a system of five scalar equations for the

unknown functions

()

xxt= and for the parameters

λ and

λ , which specify the

constraint force.

We notice that, in the case of the rheonomic constraints,

MECHANICAL SYSTEMS, CLASSICAL MODELS

390

grad d d 0

αα

⋅



r , 1, 2α

Figure 6.7. Motion of a particle constrained to stay on a curve C.

the real work of the constraint forces is written in the form

(

)

11 22 1122

ddgraddgradd d

Wfffftλλ λλ=⋅ = ⋅ + ⋅ =− +



Rr r r ,

being non-zero; indeed, taking into account the variation in time of the curve, the real

displacement of the particle is not tangent to the curve frozen at the moment

t , in the

normal plane of which is the constraint force

R .

If the constraint is scleronomic or, at least, catastatic, then the work

W = ; in

this case, the curve

C is fixed and the trajectory coincides with it, the constraint force

belonging to the normal plane to the trajectory at the point

P . In the theorem of kinetic

energy (6.2.9), the constraint force does no more appear, and we may specify the

position of the particle on the trajectory. The parametric representation (6.2.2) becomes

()

xxq= , 1, 2, 3i = , so that we obtain

(

)

(,;)

xxq Qqqt q

′′



(6.2.17)

where

d()/d

xxqq

′

, while (,;) (,;) (,;) ()

Qqqtq t F qqtx q

⋅=



 Frr r , which

determines the generalized co-ordinate

()qqt

. In particular, if the given force

depends only on the position of the particle (

()

FFr), then we have ()QQt= , so

that

()

()d

vv Qηη−=

∫

Noting

() ()d

qvQ

xx m

ϕηη

⎡

⎤

⎢

⎥

′′

⎣

⎦

∫

(6.2.18)

the equation (6.2.17) becomes