Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

Problems of dynamics of the particle

411

the trajectory coincides with that imposed if and only if

 , so that we may state

Theorem 7.1.1'. The trajectory of a free particle in a resistent medium, modelled by the

relation (7.1.21), is rectilinear if and only if the resultant of the given forces acting

upon it has a fixed direction, and its initial velocity has the same direction.

Analogously, proceeding as in Subsec. 1.1.2, we obtain

Theorem 7.1.2'. The trajectory of a free particle in a resistent medium, modelled by the

relation (7.1.21), is a plane curve if and only if the resultant of the given forces acting

upon it is parallel to a fixed plane (is normal to a fixed direction), and its initial

velocity has the same property.

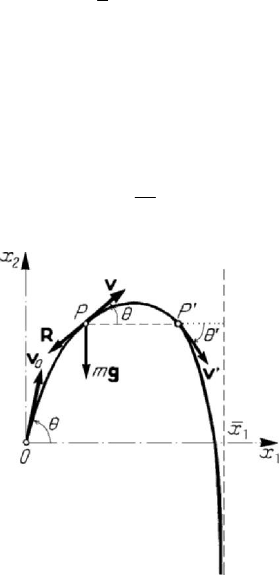
In the case of a heavy particle

in a resistent medium, the equation of motion is

()gvϕ

−

 

rg r,

(7.1.22)

where we assume that – in general – the initial velocity

v is not directed along the

vertical of the position of launching (

v has not the same direction as g );

corresponding to the Theorem 7.1.2', the trajectory is a plane curve (contained in a

vertical plane). Using Frenet’s trihedron, we may write

[

]

sin ( )vg vθϕ=− + ,

cos

g θ

= ,

(7.1.22')

Figure 7.4. Motion of a heavy particle in a resistent medium.

where

θ is the angle made by the velocity v with the

Ox -axis. We notice that

cos 0θ ≥ , hence /2 /2πθπ−≤≤; the concavity of the trajectory is directed

towards the negative ordinates (Fig.7.4), so that to

d0s > corresponds d0θ < (the

angle

θ is decreasing). It follows d/d d/dsvtρθ θ

−=− , so that the second

equation (7.1.22') takes the form

cosvgθθ=−



(7.1.22'')

MECHANICAL SYSTEMS, CLASSICAL MODELS

412

We have thus obtained a system of two differential equations (7.1.22'), (7.1.22'') for the

unknown functions

()vvt= and ()tθθ

, with the initial conditions

(

)

vt v= ,

(

)

tθθ= . Eliminating the time t , we may write the equation

()

tan

dcos

θθ

⎡

⎤

⎢

⎥

⎣

⎦

(7.1.23)

which defines the function

()v θ with the initial condition

(

)

vvθ

. This equation

of the hodograph of motion, which can be written also in the form

d( cos )

()

(7.1.23')

is the basic equation of the external ballistics. The equation (7.1.22'') allows then to

determine (usually, one takes

)

cos

=−

∫

(7.1.23'')

wherefrom – afterwards – we may obtain

()tθθ

. Noting that

dcosdxv tθ=

d sin dxv tθ=

, there result the parametric equations of the trajectory in the form

()dxx v

ϑϑ=−

∫

()tandxx v

ϑϑϑ=−

∫

(7.1.23''')

where we take

0xx== if the particle (the projectile) is launched from the origin

O . In the case of an object launched from an airplane at the height h we take

0x = ,

xh= ; the initial velocity

v is the velocity of the airplane at the moment of

launching the object.

From the second equation (7.1.22') one observes that (

θ is only decreasing and

greater than

/2π− for t finite, hence cos 0θ > ) the velocity v is finite and non-

zero. An extreme value of

v is given by d/d 0vt

; we obtain thus () sinvϕθ=− .

Because the velocity

v is finite, from (7.1.22'') it follows that θ has an extreme value

for

d/d 0tθ = , hence for cos 0θ

; but the angle θ is decreasing, so that we have

lim / 2

θπ

→∞

=− . We notice that for vv

∗

> ,

(

)

1vϕ

∗

, we have 0v



, the function

()vϕ being monotone decreasing. Hence, the velocity v has an inferior limit (

0v >

)

and a superior one (

∗

≤ ). The trajectory has a vertical asymptote

xx= , with

lim ( )dxxv

ϑϑ

−

→− +

∫

(7.1.24)

Problems of dynamics of the particle

413

and the corresponding velocity is given by

/2 0

lim ( )vv

θπ

∗

→− +

. Because of the

resistance of the air, we notice that the range of throw of the projectile is smaller.

Besides, for two points

P and P

′

of the trajectory, which have the same ordinate

x ,

it results

θθ

′

< ; hence, the two branches (increasing and decreasing) of the

trajectory are not symmetric. Applying the theorem of kinetic energy, we may write

(

)

d/2 d ()dmv mg x mg v v tϕ=− − , so that, integrating between the points ()Pt

and

()Pt

′′

, we obtain

()

[]

() ()d 0

vv g vvϕτ ττ

′

−=− <

∫

wherefrom

0vv

′

>>.

Modelling the projectile as a rigid solid, one can take into account also its rotation,

being led to a deviation from the vertical plane of the trajectory.

In particular, d’Alembert has considered the law of resistance

()

vvϕλ= ,

0n >

λ being a positive constant with dimension. The equation (7.1.23') leads to

(cos)

cos

λθ

= ;

integrating, we get

[]

()

{}

00 0

cos

1()()cos

λε θ ε θ θ

−−

(7.1.25)

where we have introduced the integral

()

cos

εθ

∫

(7.1.25')

For small velocities, one can use Stokes’ law ( 1n

); thus, we obtain

() tanεθ θ= ,

so that

()

cos

()

cos sin

θλ θθ

−−

(7.1.25'')

For velocities till 250 m/s one may take

, obtaining Euler’s law; we notice that

(

)

1tan

() lntan

2cos 4 2

θπθ

εθ

⎡

⎤

=+ +

⎢

⎥

⎣

⎦

(7.1.26)

Let us consider now

n ∈  ; for n odd (

21np

−

), we have

MECHANICAL SYSTEMS, CLASSICAL MODELS

414

21 221

2 ( 1)( 2)...( )

sin

() sec sec

2 1 (2 3)(2 5)...(2 2 1)

ppk

pp pk

ppppk

εθ θ θ

−

−−−

−− −

⎡⎤

⎢⎥

−−−−−

⎣⎦

∑

(7.1.26')

while for

n even ( 2np= ) we may write

222

(2 1)(2 2)...(2 2 1)

sin

() sec sec

2 ( 1)( 2)...( )

ppk

pp pk

εθ θ θ

−

−− −+

⎡⎤

⎢⎥

−− −

⎣⎦

∑

(

)

(2 1)!!

ln tan

2! 42

πθ

−

(7.1.26'')

The velocity

()v θ is then easily given by the formula (7.1.25), obtaining the time t

and the parametric equations of the trajectory from the formulae (7.1.23''), (7.1.23''').

Legendre considers the resistance law

()

vvϕλμ

+ , where ,, 0nλμ > , while

1μ < (otherwise, the particle – without initial velocity – comes against a resistance

mgμ and can no more fall); also in this case, the problem may be solved by

quadratures.

We observe that, by the substitution

[

]

sin ( ) 1/vvyθϕ

= , the equation (7.1.23)

reads

23 2

d()

() 1 2 ()

vv y vv y

ϕϕ

⎡

⎤

=−−+

⎡⎤

⎣⎦

⎢

⎥

⎣

⎦

;

(7.1.27)

Drach has determined all the forms of the function

()vϕ for which the solution of this

equation may be obtained by quadratures.

1.2.3 Rectilinear motion of a heavy particle

If, in the motion of the heavy particle

P considered above, the initial velocity

vanishes (

=v0) or is collinear with g , then the trajectory is rectilinear (along the

local vertical). Taking the

Ox -axis along the direction of the gravity acceleration g ,

the equations (7.1.14) become

()()

0000

xgtt vttx

−+ −+,

(

)

vgtt v

−+,

(7.1.28)

for the motion in vacuum, with the initial conditions

(

)

xt x

(

)

vt v= ; taking

0t = and

0x = , we may write

xgtvt=+

vgtv

+ ,

(7.1.28')

without loosing anything from the generality.

Problems of dynamics of the particle

415

Eliminating the time

t between the equations (7.1.28), we obtain the relation

between the velocity

v and the co-ordinate x in the form

()

2vv gxx=+ −,

(7.1.28'')

corresponding to Torricelli’s formula (7.1.17). A particle which is falling with the

initial velocity

v from a height h (in this case

0xx

−

> ) comes down with the

velocity

2vv gh=+ after an interval of time

()

(

)

/12/1vg ghv

− . A

particle which is thrown up with the initial velocity

v (in this case

0xx

−

< ) attains

the height

/2hv g= after an interval of time

/vg; after another interval of time

/vg, the particle comes back to the initial position with the same velocity

v .

In the case of a resistent medium, it is convenient to distinguish between the

descendent and the ascendent motion along the local vertical. In the first case, if we

assume an initial velocity

0v > , with the same direction as the Ox -axis, then the

equation (7.1.22) leads to

[

]

[

]

1() ()()vg v g v vϕϕϕ

∗

=− = −



(7.1.29)

the velocity

∗

being introduced in the previous subsection. It results that

() ()

ϕϕη

∗

−

∫

(7.1.29')

and we may obtain

()vvt= ; noting that ddxvt

, we get also

() ()

ηη

ϕϕη

∗

−

∫

(7.1.29'')

∗

< , then () ()vvϕϕ

∗

− is positive at the beginning, while the equation (7.1.29)

shows that the velocity

v increases. From (7.1.29') we notice that for vv

∗

→ we have

t →∞, so that v

∗

is a superior limit for the velocities; hence, the velocity v increases

till this limit. Analogously, if

∗

> , then the velocity v decreases till the limit value

∗

(in this case 0v <



). We may thus state that, for any initial velocity

v , the particle

falls with a velocity which tends to become uniform (tends to

∗

for t →∞); if

∗

= , then the motion of the particle is uniform.

If a heavy body, which may be modelled by a heavy particle, is launched by a

parachute, then the velocity is – at the beginning – increasing (a motion approximately

uniform accelerated, as in vacuum, the resistance of the air being negligible); when the

parachute is opening, the resistance of the air increases very much and the falling

velocity tends to

∗

(a motion approximately uniform). As well, let us consider two

equal bodies (e.g., two whole spheres, of the same radius, but of different matter),

modelled by two particles of masses

m and

m ; at equal velocities, these bodies come

MECHANICAL SYSTEMS, CLASSICAL MODELS

416

against the same resistance of the air. Hence,

11 22

() ()mg v mg vϕϕ

, where

()vϕ

and

()vϕ are the functions corresponding to the forces

RR. Observing that

11 22

() () 1vvϕϕ

∗∗

== and making

∗

, we may write

()vϕ

∗

(

)

/mm=

()vϕ

∗

1= , so that

21 1 2

() /vmmϕ

∗

; hence, if

mm> , then it

results

21 22

() () 1vvϕϕ

∗∗

>=, so that

∗

> . We may thus state that the heaviest

particle has a limit velocity of falling in the air greater than that of the lighter one.

If the motion is ascendent and if we assume an initial velocity

0v > directed in the

same direction as the

Ox -axis (taken in the opposite direction of the gravity

acceleration

g ), then the equation (7.1.22) reads

[

]

1()vg vϕ

−+



;

(7.1.30)

we find thus

1()

ϕη

=−

∫

1()

ηη

ϕη

=−

∫

(7.1.30')

The particle attains a height

1()

gvϕ

∫

(7.1.30'')

after an interval of time

1()

∫

(7.1.30''')

() 0vϕ ≡ , then we notice that one obtains greater values for h and t (the integrand

will be greater); hence, a heavy particle launched up along the vertical, with an initial

velocity

v , reaches in the air a smaller height in a shorter time as in the vacuum.

After an interval

t of time, the particle stops and then comes down, as in the previous

considerations, and – by coming down – has an initial zero velocity (hence, smaller than

∗

). The particle reaches the initial position with a velocity

v , specified by the

relation

1()

−

∫

as it results form (7.1.29''); comparing with the relation (7.1.30''), in which the integrand

is smaller, we notice that

, so that in the air the falling velocity is smaller than

the launching one. One returns to that position after an interval of time

1()

−

∫

Problems of dynamics of the particle

417

To compare with the relation (7.1.30'''), we observe that

1()

vϕ

−

;

as well

11d

1()

gvg

−

We get

()

(

)

d10

1()

−

=− ≥

so that

tt> (because for

we have

0tt

= ); hence, in the air, the

falling time is greater than that of rising (for the same height

h ).

The integrals may be easily calculated for

()

vvϕλ

, n

∈

 , 0n > , λ positive

constant.

1.2.4 Motion of a heavy particle constrained to stay on a curve

Let

P be a heavy particle constrained to move on a fixed curve C , neglecting the

resistance of the air; assuming that the

Ox -axis is directed along the local vertical,

opposite to the gravity acceleration, we may write the conservation theorem of

mechanical energy in the form

mmgxh

−+, consth

wherefrom

2( )vgax=−,

(7.1.31)

Let be the plane

Π of equation xa

and P

′

the projection of the particle P on this

plane; the velocity of the particle

P is, in this case, given by

2vgh= , hPP

′

(7.1.31')

and is equal to that of a heavy particle which falls from

′

in P , without initial

velocity.

Let us suppose that the curve

C is closed. If the curve does not pierce the plane Π ,

that one being above it (we may assume to have an initial velocity

v for any initial

position

P of applicate

x , so that

/2ax v g=+ be as great as we wish), then the

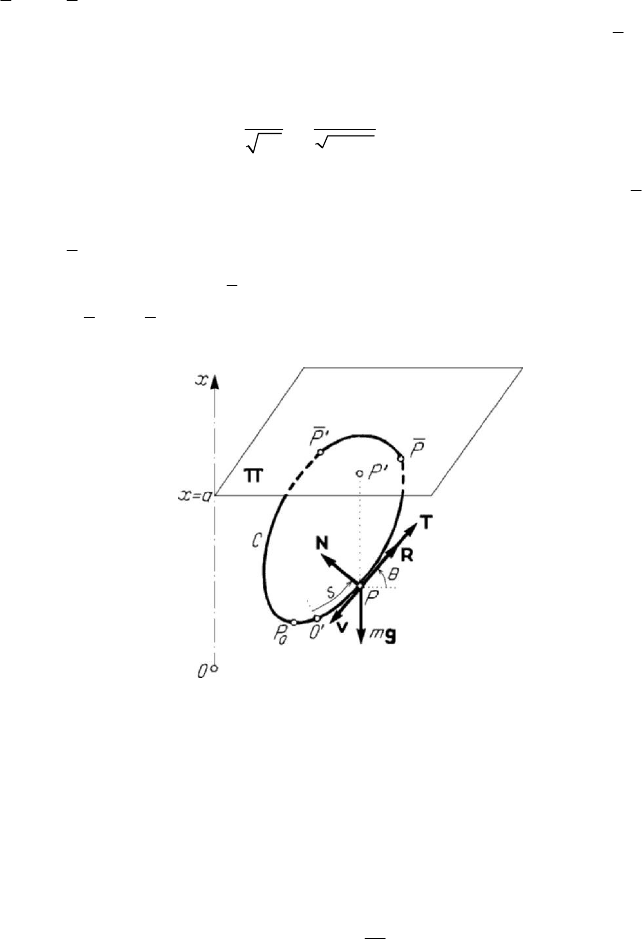
MECHANICAL SYSTEMS, CLASSICAL MODELS

418

formula (7.1.31') shows that the velocity does never vanish; the motion is periodic, the

point of maximal applicate having the minimal velocity, while that of minimal applicate

has the maximal one.

If the velocity

v is not sufficient great, the plane pierces the curve C at the points

P and P

′

(Fig.7.5). We suppose that the particle is launched from the point

P of

minimal applicate

x with the initial velocity

v ; it reaches the point P after an

interval of time

−

∫

(7.1.32)

where

ddsvt

is the element of arc on the arc



PP. If the tangent at P is not

horizontal, then the particle returns at

P in a time T with the velocity

v and then

reaches

′

in a time T

′

, which is calculated by the same formula (7.1.32), ds being

an arc element on the arc



′

. Hence, the motion of the particle is oscillatory between

the points

P and P

′

, each simple oscillation being of duration TT

′

Figure 7.5. Motion of a heavy particle constrained to stay on a curve.

Let us consider now that the motion of the particle is with friction in a resistent

medium; for the sake of simplicity we assume that the curve

is situated in a vertical

plane. We choose an origin

′

for the curvilinear co-ordinate s . As well, we introduce

the normal constraint force

N , the tangential constraint force vers

−Tv, where

is the sliding friction coefficient, and the resistance ()versmg vϕ

−Rv. The

equations of motion in intrinsic co-ordinates are written in the form

[

]

sin ( )mv mg v fNθϕ=− − +



cos

mNmgθ

=− ,

(7.1.33)

Problems of dynamics of the particle

419

where

ρ is the curvature radius, while θ is the angle formed by the tangent to the

curve

C with the horizontal line. Eliminating the constraint force N between the two

equations and noting that

(

)

2d /dvvs=



, we obtain the equation

(

)

[]

2sin cos () 2

gf vf

θθϕ

=− − − + ,

(7.1.33')

which determines the unknown function

()vvs

; then one may calculate s and t by

quadratures. The points on the curve for which

sin cos sin( )/ cos 0

θθθϕϕ

−

=− =

hence for which

θϕ= , where ϕ is the angle of sliding friction, represent limit

positions of equilibrium for the particle.

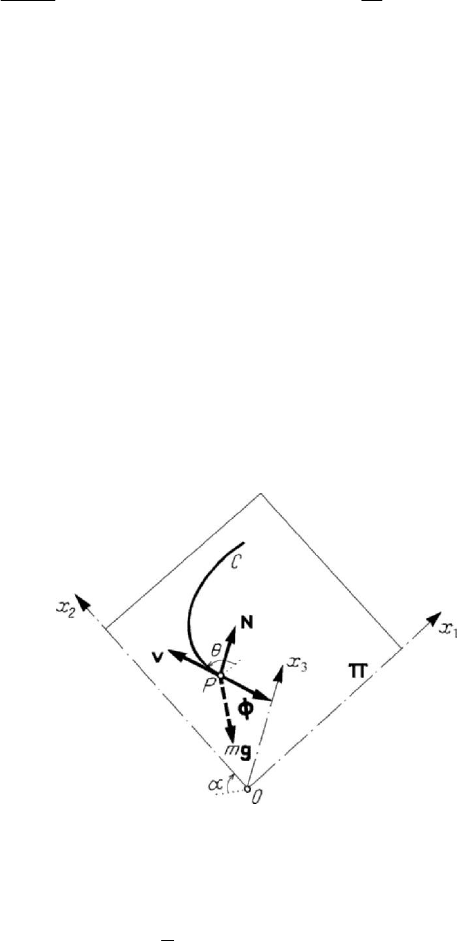
1.2.5 Motion of a heavy particle constrained to stay on a plane

Let be a heavy particle

P situated on a plane Π which makes the angle

0/2απ<≤ with the horizontal plane (Fig.7.6). Assuming a sliding friction of

coefficient

tan

ϕ= , the force of friction is Φ ,

NΦ

≤

, where N is the constraint

force, normal to the plane; taking into account the condition (4.1.50) and observing that

the given force has the magnitude

Fmg

and the normal component

cos

Fmgα=− , it results the condition of equilibrium

cos cosαϕ≥ . Hence, if

the angle

α is at the most equal to the angle of friction, then the particle is in

equilibrium in any position.

Figure 7.6. Motion of a heavy particle constrained to sliding friction on a plane.

If the particle is in motion and the mentioned condition is not fulfilled, then its

position will be given by the equation

mmfN

=− +



rg N

, cosNmg α

(7.1.34)

MECHANICAL SYSTEMS, CLASSICAL MODELS

420

in the plane

0x = ; choosing the axes

Ox (the intersection of the plane Π with the

horizontal one) and

Ox in this plane, we obtain

cos sin cos cosxv v fgθθθ αθ=− =−





sin cos sin cos sinxv v g fgθθθ α αθ=+ =−−





where

is the angle made by the velocity v with the

-axis. It results

cos sin sinvfg gααθ=− −



, sin cosvgθαθ=−



wherefrom

(

)

dcot

tan

dcos

θθ

;

(7.1.34')

this equation is of the form (7.1.23) and it may be analogously studied. Noting that

cot const

α = , we get

(

)

(

)

cot

cos cos tan cot

42 42

ππθ

θθ

⎡⎤

=−−

⎢⎥

⎣⎦

(7.1.34'')

and then

()d

sin

xx v

ϑϑ

=−

∫

()tand

sin

xx v

ϑϑϑ

=−

∫

(7.1.34''')

with

/2πθθ−<≤. We notice that

/2 0

for cot 1,

lim

0 for cot 1,

θπ

→− +

∞

⎧

⎪

⎨

⎪

⎩

assuming that

/2θπ< .

In the case of a horizontal plane (

0α

) it results

0θ



, hence

θθ= ; the motion

is rectilinear and uniformly delayed. The equation (7.1.34) can be decomposed in two

equations

mfN

=−



=gN 0

(7.1.35)

as the vectors are contained in the

Π -plane or are normal to this one. There results

Nmg= and the velocity

()

−

∫

vv ,

(7.1.35')